考慮波浪破碎沖擊力的鋼管樁水平承載力的數值研究

李芙蓉，趙汝博，馬玉祥

(1.中交四航局港灣工程設計院有限公司，廣州 510290；2.廣東省海岸與島礁工程技術研究中心， 廣州 510006；3.大連理工大學 海岸和近海工程國家重點實驗室，大連 116024)

鋼管樁因其穿透能力強、自重輕和較高的承載力等優點被廣泛地應用于碼頭、橋梁、海上風電及海洋平臺等海洋海岸工程結構。在服役期間，主要承受來自于風、波浪、流及地震等產生的荷載。隨著工程建設和經濟的發展，海岸結構不斷向深水擴展，深水中海洋荷載動力環境復雜，所以對鋼管樁水平承載力也提出了更高的要求。我國東南沿海易受到臺風的襲擊，臺風期間形成的巨浪容易發展成為卷破波，卷破波卷舌部位能量巨大，可對結構物的安全造成威脅，而目前針對波浪對樁柱結構的作用主要考慮的是非破碎波浪產生的作用力，而對結構物在破碎波作用下的結構動力的響應研究非常少，因此亟需開展卷破波對鋼管樁的作用研究，為高海況下結構物的設計提供科學依據。

由于地基隨著深度的變化，其物理性質也隨之改變，通過理論分析法很難模擬土體的非線性行為，而有限元法在模擬樁土相互作用具有很大的優越性[1]。張桂平[2]和劉紅軍等[3]通過有限元研究了極端海況作用下樁基結構的承載力及樁身變形情況。趙暉等[4]分析了規則波作用下波浪入射頻率和土體參數等因素對樁基內力、變形的影響。顧棟輝[5]研究了不同波浪理論的波浪力對樁頂位移的影響，并提出海上風機相應的抗浪設計準則。上述研究主要分析的是波浪作用下樁基承載力及樁身變形，但是沒有考慮波浪破碎的影響。在水動力學研究方面，很多學者[6-9]分析了卷破波對樁柱結構的沖擊特性，結果表明卷破波可產生巨大水平沖擊力，從而可能使結構發生斷裂或傾覆，但是目前的研究主要集中在沖擊力的強度和分布范圍，還沒有考慮結構的響應和土體對結構約束的情況。

本文結合廣東某石化碼頭工程資料，基于ABAQUS建立了卷破波作用力作用于鋼管樁-地基相互作用的有限元模型，分析了卷破波作用下鋼管樁的應力和位移情況，并進一步分析了壁厚和樁徑對鋼管樁應力及水平位移的影響差異。

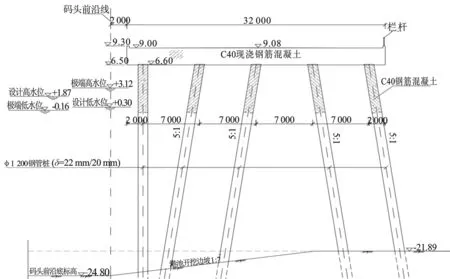
圖1 平臺結構設計圖Fig.1 Structural diagram of platform

1 工程介紹

1.1 工程概況

本文依托廣東省某地一個原油碼頭工程項目。碼頭上部由混凝土結構部件構成，主要有橫梁、面板、預應力縱梁及面層。本文選擇其中的工作平臺作為研究對象(圖1)，平臺采用鋼管樁，鋼管樁上部為樁芯混凝土,鋼管樁有直樁和斜樁(傾斜比例5:1)，樁徑為1 200 mm，泥面處的壁厚為22 mm，在混凝土灌漿段壁厚為42 mm，樁基長度為54～57 m，埋深24～26 m，泥面以上30 m左右，碼頭前沿設計底標高為-24.80 m，碼頭上部結構受力計算的下緣標高為6.50 m，極端高水位為3.12 m，設計高水位為1.87 m。

圖2 破壞的鋼管樁Fig.2 Damaged steel pipes

1.2 工程案例分析

本工程鋼管樁于2014年5月開始沉樁施工，6月份沉樁結束，然后進行穩樁拋砂和穩樁拋碎石，工程受季風影響，部分樁基發生偏位現象，在隨后的2014年～2017年受臺風蓮花、妮妲、海馬、天鴿和卡帕等影響，大部分樁基發生折斷和偏位(圖2)。從圖2中可以看出，鋼管樁折斷處基本位于泥面附近，有的部分折斷，有的全部折斷。本文將通過建立有限元模型分析鋼管樁的受力情況并判斷其破壞原因。

2 數值模型

2.1 材料參數及本構模型

表1 土體參數表Tab.1 Soil parameter

為模擬鋼管樁-土體之間的非線性，本文選擇摩爾庫倫模型。摩爾庫倫參數通過固結快剪試驗得到，土體參數如表1所示。ABAQUS中通過樁-土表面定義接觸屬性來模擬樁與土之間的剪力傳遞和相對位移，采用主-從接觸算法，選擇剛度大的樁體為主控面，土體表面為從屬面，樁-土接觸采用摩爾-庫侖罰函數摩擦形式，界面滑動摩擦系數選取u=tan(0.75φ)[10]。參考孔位學等[11]針對非關聯流動法則下巖土材料的剪脹角選取方法，本文采用非關聯流動選取ψ=φ/2。鋼管樁和土體采用6面體8節點線性減縮積分實體單元(C3D8R)建立有限元計算模型。土體模型直徑為樁徑的30倍，因此可以忽略邊界的影響[12]。

鋼管樁材質為Q345B，屬于低合金鋼，參考《鋼結構設計標準》(GB 50017-2017)[13]，當材質為Q345B時，壁厚δ在16 mm<δ≤40 mm時，鋼管樁在泥面處的屈服應力設計值為335 MPa，極限抗拉強度最小值470 MPa。因鋼材為低合金鋼，所以本文數值建模采用雙斜線模型(圖3)，其中模型二次強化剛度約為初始剛度的1%[14]。

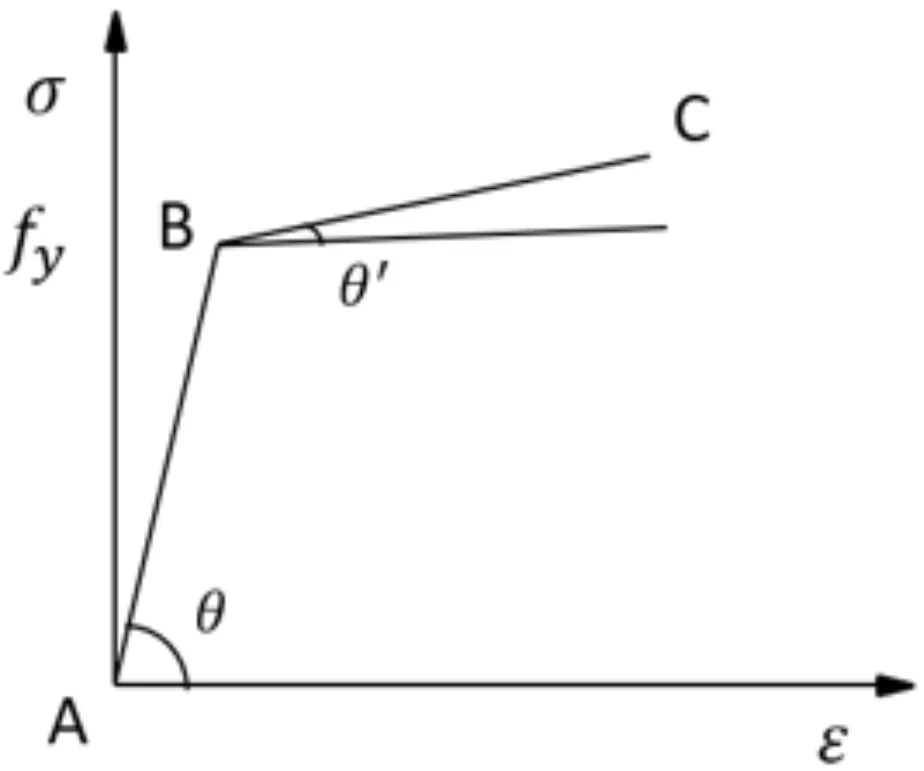
圖3 雙斜線模型Fig.3 Double slash model

2.2 模型驗證

本文采用Huang等[15]研究的高速公路樁基水平承載力試驗數據來驗證所建立模型的正確性，試驗內容包括單樁水平承載力和群樁水平承載力試驗，本文只對比單樁試驗(即試驗中的B7樁)。B7樁為鉆孔灌注樁，直徑1.5 m，樁長34.9 m，埋深34.0 m，樁身配有兩層縱筋，每層配有26根Φ32鋼筋，即總共有52根Φ32縱筋。混凝土和鋼筋的材料參數如表2所示，土體參數如表3。圖4為與試驗[15]和Cote等[12]數值模擬對比的樁頭水平位移圖，從圖可以看出，本文的數值模擬結果與試驗結果對比較好，驗證了本文所建立數值模型的可靠性。

表2 Huang等[15]試驗材料參數表Tab.2 Material parameters for the experiment of Huang et al. [15]

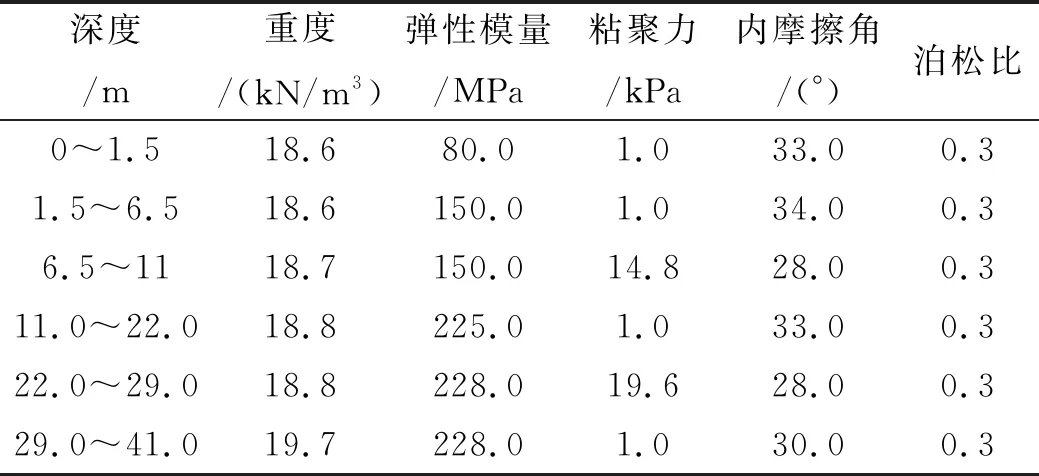
表3 Huang等[14]試驗土體參數表Tab.3 Soil parameters for the experiment of Huang et al. [15]

3 數值分析

3.1 荷載工況

圖4 樁頂水平位移Fig.4 Horizontal displacements at the pile top

本研究選取平臺處百年一遇最大波高進行研究，根據實測和數值模擬結果，工程區域臺風期間最大波高為13.72 m，周期11.6 s，水深24.5 m。由于工程事故是樁基破壞，本文不考慮由于群樁引起的繞射等波浪現象，只取單樁進行分析。Chella和Torum[16]認為破碎波對結構的作用力可分為準靜態力和沖擊力兩部分，其中準靜態力可以用莫里森公式[17]來表示，所以破碎波對結構產生的總力可表示為式(1)。破碎波產生的沖擊力采用 Goda等[6]提出的式( 2)，卷破波與樁基作用的示意圖如圖5，其公式的含義及使用在這里不再詳細介紹，具體可參考文獻[6,16]。

F=FI+FD+FS

(1)

其中FI和FD的意義可參考Morison方程[17]。

FS=0.5ρCSDV2ληb

(2)

式中：ρ為海水的密度(本文取1 025 kg/m3)；CS為沖擊力系數；λ為波浪卷曲因子；V為波浪破碎時的波速；D為圓柱直徑。

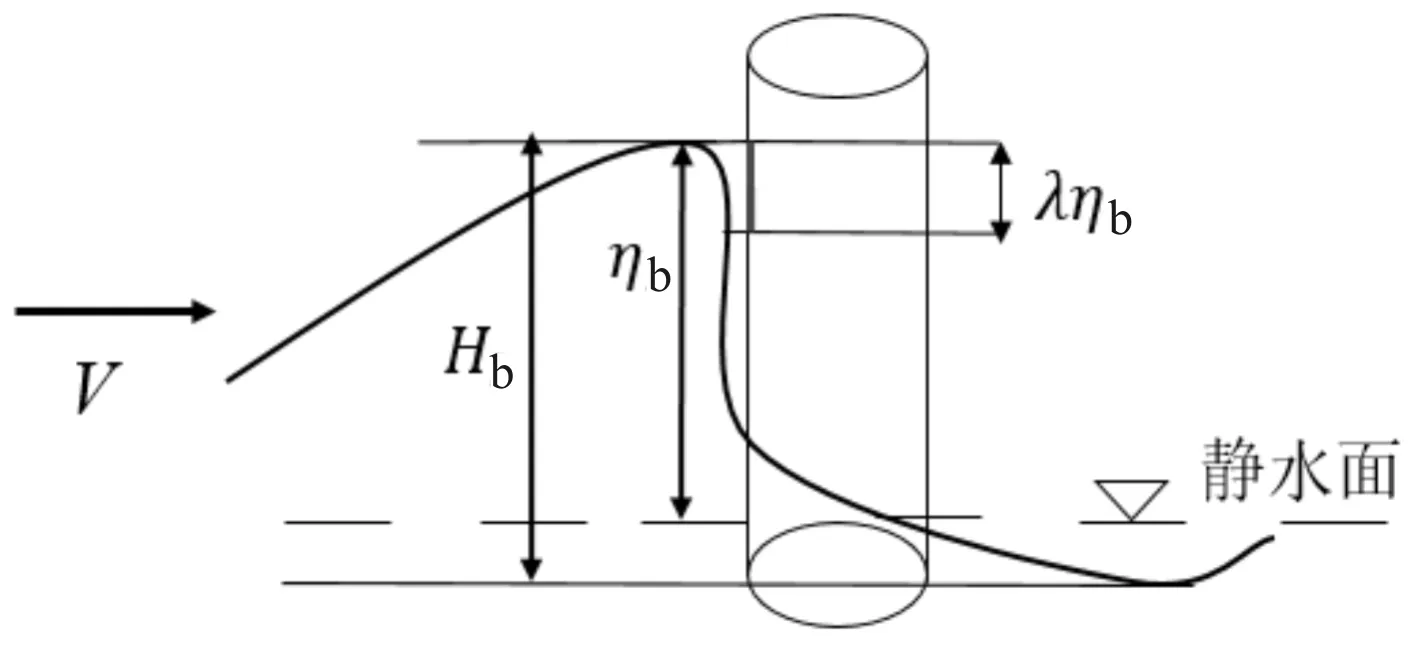
圖5 卷破波與樁基作用沖擊力示意圖Fig.5 Schematic diagram of impact force on pile foundation induced by breaking waves

3.2 結果分析

圖6和圖7分別為考慮波浪破碎和未考慮波浪破碎時樁徑1 200 mm和1 400 mm鋼管樁的樁身Mises應力云圖，表4為鋼管樁水平承載特性指標統計表，其中應力比為樁身最大Mises應力與樁身屈服應力之比。通常鋼管樁工程設計時，樁身最大Mises應力應小于樁身屈服應力，即應力比小于1。可以看出，當考慮波浪破碎時，樁身應力比均大于未考慮波浪破碎時的應力比，對于樁徑1 200mm和1 400 mm鋼管樁，其樁身應力比相比于未考慮破碎時分別增加15.0%和20.0%，但無論是否考慮波浪破碎，2種鋼管樁應力比均大于等于1。對于樁身泥面處水平位移，對于樁徑1 200 mm的鋼管樁，當考慮波浪破碎時，鋼管樁在泥面處發生折斷，而未考慮波浪破碎時，鋼管樁泥面處水平位移為97.0 cm。對于樁徑1 400 mm的鋼管樁，相比于考慮波浪破碎時，未考慮波浪破碎時其水平位移相應減少89.2%。綜合以上分析可知，對于有可能發生破碎的極端波浪與樁柱結構作用時，需要考慮波浪破碎的影響。

6-a 考慮波浪破碎6-b 不考慮波浪破碎7-a 考慮波浪破碎7-b 不考慮波浪破碎圖6 樁徑1 200 mm壁厚22 mm鋼管樁Mises應力云圖 Fig.6 Mises stress of steel pipe pile with a diameter of 1 200 mm and a wall thickness of 22 mm 圖7 樁徑1 400 mm壁厚25 mm鋼管樁Mises應力云圖Fig.7 Mises stress of steel pipe pile with a diameter of 1 400 mm and a wall thickness of 25 mm

表4 鋼管樁水平承載特性指標統計表Tab.4 Statistical table of horizontal bearing characteristics of steel pipe piles

本碼頭工程共有樁徑1 200 mm壁厚22 mm和樁徑1 400 mm壁厚25 mm的鋼管樁，本文對比了對2種鋼管樁在卷破波作用下的水平承載性能。當從樁徑1 200 mm壁厚22 mm的鋼管樁增加到樁徑1 400 mm壁厚25 mm的鋼管樁時，同時樁徑1 400 mm的鋼管樁受到的波浪力和卷破波的沖擊力也相應增加，對于考慮波浪破碎和不考慮波浪破碎情況，其應力比分別相應減少10.7%和16.0%。對于水平位移，考慮波浪破碎情況時，樁徑1 200 mm的鋼管樁發生折斷，樁徑1 400 mm的鋼管樁位移為141.7 cm，但并未折斷。對于樁徑1 400 mm的鋼管樁，當不考慮波浪破碎時，水平位移相應減少84.2%。以上結果表明，雖然樁徑1 400 mm的鋼管樁受到的波浪力和卷破波沖擊力更大，但其相比于1 200 mm的鋼管樁對減小應力比和水平位移的作用更大。即使沒有考慮破碎產生的沖擊力，兩種樁徑的鋼管樁在百年一遇極端大浪作用下均已達到破壞，考慮破碎的作用后，樁的破壞更加嚴重。由于2種鋼管樁無論在樁徑和壁厚上都有差異，下文將進一步分析鋼管樁壁厚和樁徑對水平承載特性的影響。

4 樁基水平承載特性影響因素

4.1 鋼管樁壁厚影響分析

圖8 不同壁厚的鋼管樁應力比Fig.8 Stress ratio of steel pipe piles with different wall thicknesses

本文進一步研究考慮波浪破碎情況下，鋼管樁壁厚對鋼管樁水平承載特性的影響，采用Goda等[6]提出的卷破波對樁基的沖擊力公式進行分析，在波高13.72 m，水深24.5 m工況下，分析樁徑1 200 mm和1 400 mm的鋼管樁的應力比及泥面處水平位移隨壁厚變化情況。圖8為不同壁厚的鋼管樁應力比，可以看出，當不考慮波浪破碎時，無論樁徑1 200 mm和1 400 mm的鋼管樁，其應力比隨著壁厚的增加而逐漸降低。但是當考慮波浪破碎情況時，對于樁徑1 400 mm的鋼管樁，其應力比隨壁厚的增加而減小，但對于樁徑1 200 mm的鋼管樁，當壁厚從22 mm增加到40 mm時，應力比隨之下降，當壁厚從40 mm增加到50 mm時，應力比幾乎沒有發生變化。這是因為當壁厚為16 mm<δ≤40 mm(δ為壁厚)時最低屈服強度為335 MPa，而當壁厚為40 mm<δ≤63 mm時最低屈服強度為325 MPa[13]，雖然鋼管樁壁厚從40 mm增加到45 mm其抗彎剛度在增加，但其屈服應力卻降低了，所以導致應力比沒有發生變化。樁徑1 400 mm的鋼管樁應力比一直在下降是因為其抗彎剛度的增加對應力比降低的影響作用大于其屈服應力降低對應力比增加的影響作用。表5為樁基在泥面處位移統計表。從中可以發現，無論是否考慮波浪破碎，其水平位移隨著壁厚的增加而減小。同時，當考慮波浪破碎時，水平位移減小的速度大于未考慮波浪破碎時的情況。當未考慮波浪破碎時，壁厚從30 mm增加到50 mm時，樁徑1 200 mm和1 400 mm的鋼管樁水平位移分別減小28.7%和26.0%，當考慮波浪破碎時，樁徑1 200 mm和1 400 mm的鋼管樁水平位移分別減小90.2%和56.0%。當壁厚逐漸增大時，水平位移減小的相應程度在降低。以樁徑1 400 mm鋼管樁為例，當壁厚從30 mm增加到40 mm，考慮波浪破碎和不考慮波浪破碎時分別相應減小52.3%和19.1%，當壁厚從40 mm增加到50 mm，考慮波浪破碎和不考慮波浪破碎時分別相應減小9.6%和8.5%。當考慮波浪破碎時，對于樁徑1 200 mm的鋼管樁，當其壁厚為50 mm時應力比為0.98，此時剛剛滿足工程設計要求，而對于樁徑1 400 mm的鋼管樁，當其壁厚為40 mm時應力比為0.97，此時就已滿足工程設計要求。

4.2 鋼管樁樁徑的影響分析

表5 不同壁厚的鋼管樁水平位移統計表Tab.5 Horizontal displacement statistical table of steel pipe piles with different wall thicknesses cm

樁徑是影響樁基承載力重要因素之一，但對于卷破波作用下樁徑對鋼管樁水平承載特性研究較少。通過Morison方程[17]和式(2)可知，隨著樁徑的增大，鋼管樁受到莫里森方程的波浪力及卷破波對鋼管樁的沖擊力也隨之增大。圖9為鋼管樁隨樁徑變化的應力比。可以看出，當不考慮波浪破碎時，應力比隨著樁徑的增加而逐漸降低。當考慮波浪破碎時，對于壁厚40 mm的鋼管樁，應力比隨著樁徑的增大而降低，但對于壁厚30 mm的鋼管樁，當樁徑從1 200 mm增加到1 400 mm時，應力比降低明顯，當樁徑從1 400 mm增加到1 800 mm時，應力比基本沒有變化。因為鋼管樁樁徑的增加，抗彎剛度也在增大，但鋼管樁所受到的沖擊力也隨之增大，所以應力比變化較小。從1 800 mm增加到2 000 mm，應力比略有降低。這是由于鋼管樁抗彎剛度的增加對降低應力比的影響作用大于沖擊力增加對應力比增加的影響作用。表6為樁徑對鋼管樁泥面處水平位移影響統計表。從中可以看出，無論是否考慮波浪破碎，水平位移都隨著樁徑的增大逐漸減小，而且當考慮波浪破碎時樁徑的增加對位移減小的影響程度大于未考慮波浪破碎時的情況。當未考慮波浪破碎時，樁徑從1 200 mm增加到2 000 mm時，壁厚30 mm和40 mm的鋼管樁水平位移分別減小33.7%和31.3%，當考慮波浪破碎時，壁厚30 mm和40 mm的鋼管樁水平位移分別減小91.3%和39.3%。當考慮波浪破碎時，對于壁厚30 mm的鋼管樁，當其樁徑為2 000 mm時應力比為0.95，此時剛剛滿足工程設計要求，而對于壁厚40 mm的鋼管樁，當其樁徑為1 400 mm時應力比為0.97，此時就已滿足工程設計要求。

圖9 不同樁徑的鋼管樁應力比Fig.9 Stress ratio of steel pipe pile with different pile diameters

表6 不同樁徑的鋼管樁水平位移統計表

5 結論

本文基于ABAQUS建立了鋼管樁-地基的有限元模型，分析了卷破波作用下鋼管樁水平承載特性，通過與已有試驗對比驗證了數值模型的有效性及合理性，依據破碎波浪沖擊理論，進一步研究了卷破波作用下不同壁厚和樁徑的鋼管樁承載特性，并進行了一系列影響分析，結論如下：

(1) 對于樁徑1 200 mm的鋼管樁，在波高13.72 m，周期11.6 s的波浪作用下，考慮波浪破碎時，鋼管樁在泥面處發生斷裂。當不考慮波浪破碎時，鋼管樁樁身在泥面處只發生屈服，說明在工程區域波浪容易發生破碎時，工程設計中需要考慮波浪破碎的影響。

(2) 當考慮波浪破碎時，鋼管樁的壁厚和樁徑的增加對水平位移減小的影響程度大于不考慮波浪破碎時的情況，隨著壁厚的增大，水平位移減小的相應程度在降低。鋼管樁樁徑增加，鋼管樁抗彎剛度和受到卷破波的沖擊力也隨之增加，當抗彎剛度的增加對應力比減小的作用大于卷破波沖擊力對應力比增加的作用時，應力比才會降低，否則應力比不會降低。

致謝：本文的計算工作得到了大連理工大學超級計算中心的支持。