基于射線跟蹤的大規模MIMO信道建模①

姚俊良,劉 慶,張 琰,姚文雷

1(西安理工大學 自動化與信息工程學院,西安 710048)

2(西安電子科技大學 通信工程學院,西安 710071)

隨著智能手機的迅速普及與無線通信技術的快速發展,人們對無線數據的傳輸需求呈現爆炸式增長.第五代移動通信(5G)旨在面向2020年的移動通信應用需求,研究可以支持業務總速率高達 10 Gbps,空中接口頻譜效率和功率效率較4G均提升10倍以上的新一代無線通信系統[1,2].為了達到上述目的,新型的網絡體系架構、組網技術、新型天線陣列結構[3]及頻譜開發利用[4]等技術是研究的重點.作為無線通信重要的物理層技術,MIMO (Multiple Input Multiple Output)[5]通過在收發端使用多天線陣列,可以獲得空間復用增益,頻譜利用率得到顯著提升.研究表明,在不增加帶寬的前提下,MIMO的空間復用增益與 m in{N,M}呈線性增長關系,其中N和M分別表示接收端和發射端陣列的天線元素個數.因此,為了大幅度提升無線頻譜效率,滿足用戶對無線傳輸速率指數上漲的需求,通過增加基站天線數目構建大規模MIMO系統,是一種高效且相對便捷的方式.

大規模MIMO[6]是貝爾實驗室科學家Marzetta在 2010年底提出來的概念,也稱做 Massive MIMO.與傳統MIMO相比,大規模MIMO采用巨型陣列尺寸和多維陣列結構,能夠大幅提升無線頻譜效率,滿足用戶對無線傳輸速率指數上漲的需求,成為下一代無線通信重要的物理層技術之一.作為系統性能評估和算法設計的重要基礎,大規模MIMO信道建模理論和實現還存在著許多問題需要解決[7-10].

在大規模MIMO中,不同位置的陣列單元會處于不同的散射環境,散射簇對信道統計特性的影響很大[11].特別是對于大規模平面陣,俯仰面的散射簇分布會隨著高度的不同而有差異.研究學者通過調整本地散射簇的分布和數量,來模擬不同的無線場景[12-14].利用圓柱體陣列和等距線陣,對大規模MIMO的信道特征進行測量分析,發現散射簇輻射的電磁波并不能到達所有陣列天線,這驗證了近場效應的存在[15,16].進一步通過對 COST 2100模型[17,18]的關鍵參數進行擴充,以適用于大規模MIMO.文獻[19]在散射簇橢圓分布的基礎上,首次提出針對單極化大規模線陣MIMO的理論信道模型,并分析了散射簇生滅對信道建模帶來的影響.基于該理論,文獻[20]建立了具體的信道模型實現算法,并對大規模MIMO的統計特性進行了仿真.

近年來,基于射線跟蹤[21-25]的確定性信道建模方法成為業界研究的熱點,理論上,射線跟蹤信道建模能夠滿足大規模MIMO對無線信道的所有要求,但它存在著算法復雜度高、需要精確地圖信息的缺點.2015年,METIS項目組在現有算法基礎上,提出了基于地圖的射線跟蹤信道模型[26],模型綜合了統計信道建模和確定性建模各自的優點,能夠符合大規模MIMO信道建模的要求.

在上述研究基礎上,本文提出兼顧模型準確性和計算復雜度的大規模MIMO信道模型.所提模型的主要特點包括:基于球面波建立信道模型統一框架,因此能夠適用于大規模MIMO場景;采用基于馬德里格地圖的射線跟蹤算法對模型參數進行求解,避免了實際場景地圖制作困難的問題,提升了信道模型的實用性;采用Berg遞歸模型[26]代替傳統的UTD繞射理論,在基本不影響算法性能的前提下,有效降低了射線跟蹤算法的計算復雜度;最后利用所提算法,對信道模型的時延擴展,功率時延譜,散射簇分布以及算法運行時間進行了計算分析.

1 大規模 MIMO 信道模型

1.1 信道模型基本框架

在對大規模MIMO信道進行建模之前,首先要分析清楚陣列規模的影響.傳統MIMO模型假設散射簇和收/發天線的距離滿足遠場條件,即:

上式中R是散射簇到收/發端的距離,L是天線陣列尺寸,λ是電磁波波長.此時,電磁波以平面波到達天線陣列,陣列的空間向量具有導向矢量形式.而隨著陣列尺寸的增大,式中L增大,在R和 λ 不變的情況下,式(1)的關系將不再滿足.并且,由于陣列尺寸的增大,散射簇并非對所有陣列元素有效.

圖1所示為收發端都采用平面陣大規模MIMO的信道鏈路示意圖.平面陣中每個點由一對正交極化天線組成.空間不同位置天線所處的散射環境也是不同的,例如,收發端紅色陣元受散射簇 1 的作用,而藍色陣元受散射簇N的影響,黃色陣元則存在直射徑,信道模型需要能夠反映上述特點.另外,大規模也會影響極化矩陣的建模.傳統MIMO中,極化矩陣只與多徑有關系,而與天線無關.換言之,對于同一條多徑,收發端不同天線對應的極化矩陣是相同的.而在大規模MIMO中,散射環境的不同,使得極化矩陣與天線也有關系.

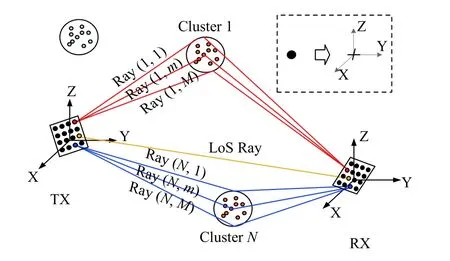
圖1 平面陣大規模 MIMO 鏈路示意圖

通過分析天線空間與傳播空間的映射投影,以及散射簇對電磁波的作用,在全局統一坐標系和簇時延線模型架構下,針對雙極化平面陣大規模MIMO,我們建立的信道模型基本框架如下:

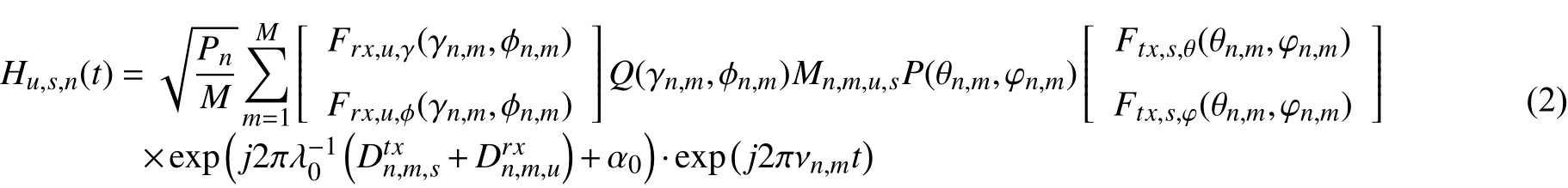
上式中,u和s表示接收天線和發射天線的序號,n和m表示主徑號和子徑號.Ftx,s,θ和Ftx,s,φ分別為天線元素s在俯仰角 θn,m和水平角 φn,m方向上的電場分量,它需要根據實測方向圖和天線姿態來計算.矩陣P為Ftx,s,θ和Ftx,s,φ向傳播坐標系的轉換矩陣,它是角度( θn,m,φn,m)的函數.接收端的符號定義與發射端類似.分別表示散射簇到接收天線u和到發射天線s的距離.Mn,m,u,s表示無線傳播環境中的極化矩陣.

由于大規模MIMO不能再假設為平面波到達,因此收發端不同位置天線的相位表示與傳統MIMO不同,式(2)中使用散射簇到收發端天線的距離來計算相位.

1.2 天線姿態對信道模型的影響

三維空間中信道模型包含天線、無線傳播以及二者的有機結合.實際中,天線陣列會由于覆蓋要求、工程需求等原因位于不同的朝向姿態,本節分析三維情況下天線姿態對信道模型的影響.

以發端天線為例,式 (2)中Ftx,s,θ(θn,m,φn,m)和Ftx,s,φ(θn,m,φn,m)分別為天線元素s在全局坐標系空間角度(θn,m,φn,m)上垂直極化電場分量和水平極化電場分量,為了描述簡單,后續我們省略下標,直接以Fθ(θ,φ)和Fφ(θ,φ)來代替.而工程中所用的天線方向圖坐標系并非與模型中的天線坐標系完全對應,兩個坐標系的關系為:以全局坐標系y軸為中心逆時針旋轉角度β,即可得到天線坐標系.這里我們僅考慮兩軸轉動的情況,三軸轉動只需要執行兩次對應操作即可.

天線坐標系中垂直極化和水平極化天線方向圖分別表示為Fθ′(θ′,φ′)和Fφ′(θ′,φ′),因此我們需要分析Fθ′(θ′,φ′)、Fφ′(θ′,φ′)和Fθ(θ,φ)、Fφ(θ,φ)的對應關系.通過分析計算,其滿足的關系如下:

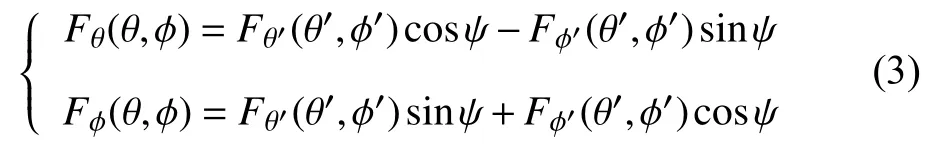
式(3)中變量:

1.3 轉換矩陣P和Q

在得到全局坐標系下的天線方向圖以后,還需要進行全局坐標系到傳播坐標系的轉換.從電場傳播的角度分析,電磁波的垂直極化電場、水平極化電場、傳播方向三者是相互垂直的,這就針對每一條傳播射線,構造了一個傳播坐標系.因此模型需要實現全局坐標系到傳播坐標系的轉換.式(2)中P(θn,m,φn,m)和Q(γn,m,φn,m)分別是發端天線和收端天線的轉換矩陣,他們都是角度(θn,m,φn,m)的函數.通過分析我們得到其表示如下:

在2D信道建模中,電磁射線僅在水平方向存在,因此式(4)中沒有了垂直角度分量.上式可以簡化為:

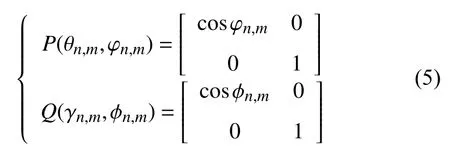
2 基于地圖的射線跟蹤算法

基于地圖的射線跟蹤算法旨在建立一個精確、更加符合實際的空間信道模型,能夠支持大規模MIMO、高級波束賦形、節點移動、高頻高帶寬等5G應用.模型基于簡化的3D地圖,采用射線跟蹤技術,考慮直射、反射、散射、繞射、透射等電磁傳播特性,墻面建模為具有特定電磁材料特性的矩形表面.計算復雜度可以通過打開/屏蔽不同的傳輸路徑來調節,同時提出一種簡單的繞射模型(Berg’s)來進一步降低復雜度,模型算法框圖如圖2.

2.1 場景地圖的建立

在全局坐標系下,確定場景范圍,給出墻體和街道的起始三維坐標.為了計算方便,假定地圖范圍位于坐標系的正半軸,即所有墻體和街道的三維坐標 滿足.為了適應大規模 MIMO 的建模,我們主要研究室外場景的建模方法.場景地圖采用馬德里格(Madrid grid),它是對真實城市結構的簡化模擬,(x,y,z)x≥0,y≥0,z≥0能比較真實地模擬不同建筑布局,反映終端運動特征和不同的蜂窩網絡部署.

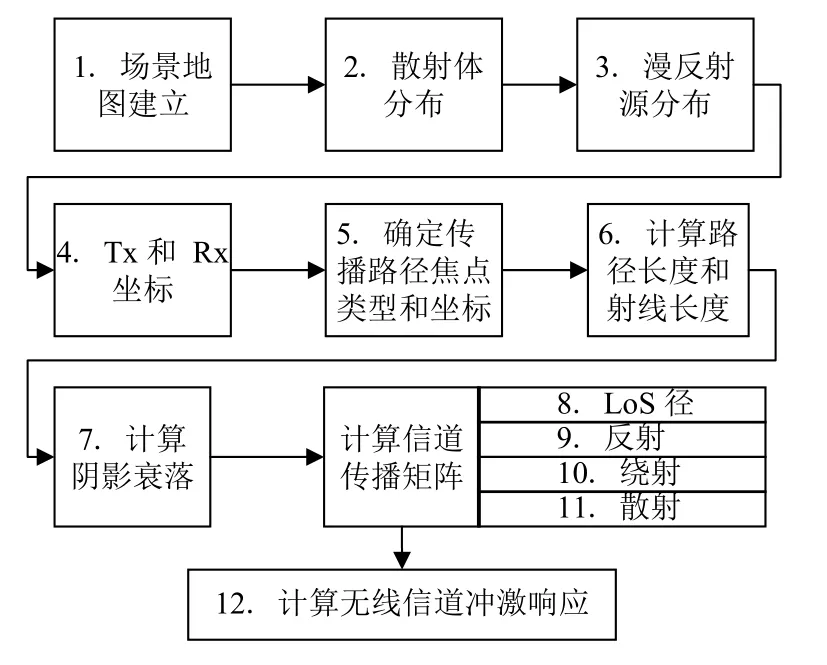
圖2 基于地圖的射線跟蹤算法

圖3和圖4分別給出了Madrid grid的三維圖和二維俯視圖,其中包含了多種城市幾何元素:正方形建筑物、長方形建筑物、樓宇入口、地鐵入口、公交站臺、停車場、人行道、停車場車道.

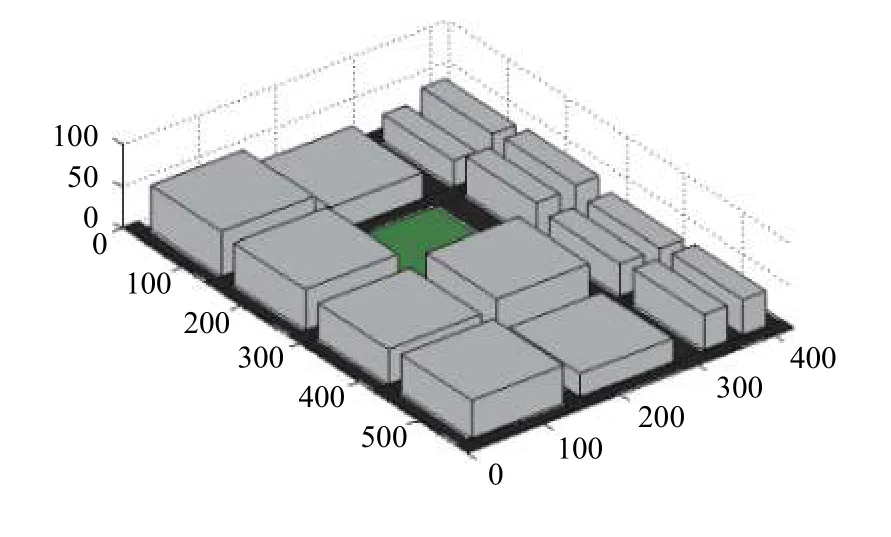
圖3 Madrid grid 三維圖示

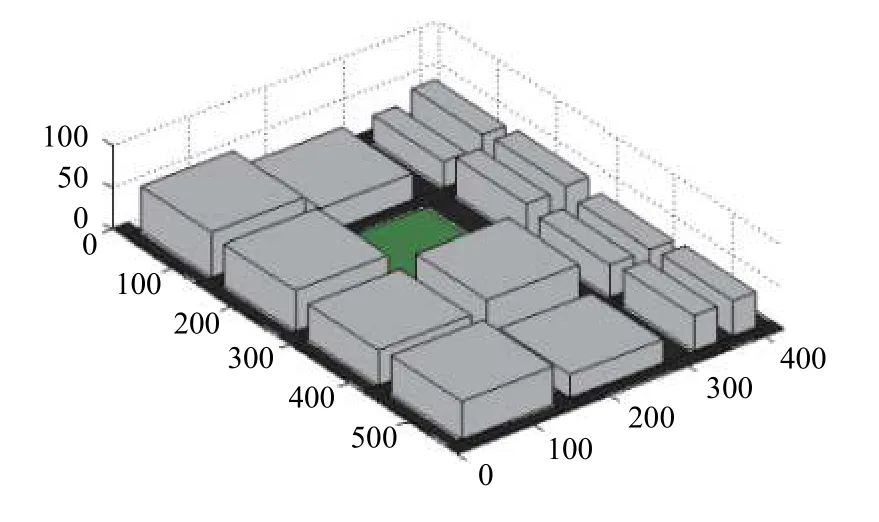
圖4 Madrid grid 二維俯視圖

2.2 確定傳播路徑上的交點類型和坐標

從一級節點TX出發,尋找所有具有以下特征的二級節點:與TX有LoS徑直達或通過一次鏡面反射可達TX,二級節點包括繞射點、散射體、漫散射源、TX鏡像點,進而可以確定交點的坐標和類型(直射、反射、繞射、散射).以二級節點為新的TX,重復上述過程獲得所有三級節點.最終將得到TX到RX的傳播路徑.本步的輸出為如下參數向量集合:

其中,K為路徑總數,Ik為第k條路徑的分段數.xki,yki,zki為第k條路徑第i個交點的三維坐標,Tk為交點類型.下面介紹不同類型交點的確定方法.

(1)反射.利用射線光學原理,以所有能被 TX“看見”的面為鏡面,得到 TX 鏡像點.從鏡像點出發,與鏡面有交點的“直射”路徑即為反射徑,與鏡面的交點為反射點.

(2)繞射.分為建筑物垂直邊繞射和建筑物頂邊繞射兩種.垂直邊繞射是與TX有LoS徑直達或通過一次鏡面反射可達TX的角邊(Corner),繞射點的x,y坐標為角邊坐標,z坐標需要在TX-RX路徑確定后才能獲得.建筑物頂邊繞射:如果收 (發)端高于樓頂,則會存在頂邊繞射 (如圖5).繞射點的確定采用 VPL(Vertical-Plane-Launch)方法:過TX和RX做一垂直平面,該平面與頂邊的交點即為繞射點.若經過一次反射到達RX,則過TX(RX)和RX(TX)鏡像點做垂直平面,平面與對應鏡面和頂邊的交點分別為反射點和繞射點.若經過兩次反射到達RX,則過TX鏡像點和RX鏡像點做垂直平面,平面與對應鏡面和頂邊的交點分別為反射點和繞射點.

圖5 建筑物頂邊繞射

常用有兩種繞射損耗計算模型:Berg’s recursive model和一致性繞射理論 UTD(Uniform Theory of Diffraction),Berg’s recursive model僅考慮繞射到陰影區域的射線,是一種有效折中復雜度和準確性的方法;UTD同時考慮繞射到非陰影區域的射線,因此路徑條數更多.圖6(a)給出Berg模型繞射線的角度范圍,其中 θT為入射波角度.圖6(b)給出UTD模型繞射線的角度范圍.在圖中TX所在位置上,Berg模型的繞射點為B點,而UTD模型的繞射點為A點和B點.

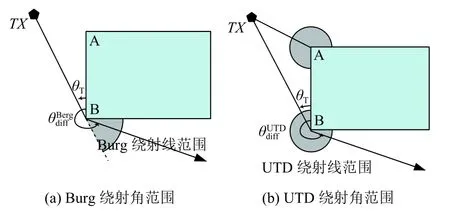
圖6 繞射角示例

(3)散射.考慮兩類散射體:第一類是 TX 或 RX 節點附近并且有LoS徑可達的散射體,第二類是在兩個節點之間、并與兩個節點都LoS可達的散射體(這里的節點可以是TX、RX、反射點、繞射點).為了降低復雜度同時又不影響模型準確性,需要舍棄滿足下述條件的弱散射體.

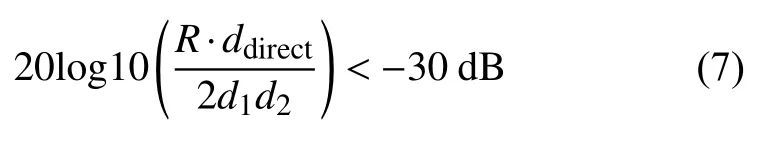
其中,R為散射體半徑,ddirect為散射體前后兩節點之間的距離,d1和d2分別為散射體到前節點和到后節點的距離.從公式(7)可以看出,小散射體/距離節點較遠的散射體都會成為弱散射體,這也符合實際情況.

采用上節介紹的射線跟蹤算法,其中繞射方式采用Berg繞射,不考慮人和車輛的散射.考慮到射線段數越多,信號衰落也越大,算法設置一條TX-RX的路徑上最多包含4個射線段,其中最多兩個繞射段.圖7給出算法的射線演示圖,圖中紅色方框為反射點,藍色方框為繞射節點.由于收發端都位于地面,因此圖中射線不包含屋頂繞射.圖中所示為NLoS場景,共包含19條路徑.

圖8給出上述19條路徑的功率時延譜 (PDP,Power Delay Profile),整體來說,隨著時延的增大,接收功率減小.但圖中功率最高的路徑并不是出現在時延最小的時候,這是因為影響路徑功率的因素除了路徑長度,還與交互點的類型有關系.從仿真結果分析,一次繞射功率損耗在 10～40 dB,一次反射功率損耗在 5～15 dB.圖中功率最高的兩條路徑不包含繞射,因此雖然路徑較長,但功率損耗整體更小.

圖7 TX-RX 的射線示例

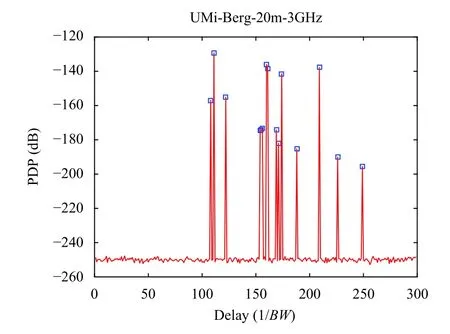
圖8 功率時延譜

3 基于射線跟蹤的信道模型分析

對于無線信道模型,模型參數的統計分布和取值是保證模型準確性的關鍵.傳統的MIMO信道模型通常采用實測方法來獲得模型參數,目前業界常用的信道測量設備包括芬蘭 Elektrobit (EB)公司的Propsound,德國 Medav 公司的 RUSK Channel Sounder以及加拿大通信研究中心(Communication Research Centre Canada,CRC)的 CRC-Chanprobe.上述測量設備受限于帶寬、通道數、載波頻率,無法直接用于大規模MIMO的信道測量.本章我們采用Mapbased射線跟蹤算法,對大規模MIMO信道模型的時延擴展和天線到散射簇距離這兩個參數進行求解.

仿真選取城市微小區 (UMi,Urban Micro)場景,基站天線高 20 m,移動臺天線高 1 m.為了模擬大規模MIMO,在馬德里格地圖的不同區域放置20個基站天線陣列,每個天線陣列包含32個(8行4列)天線元素,間距為半波長.地圖中均勻放置960個單天線移動臺.因此,該仿真場景中共包含640×960個收發天線對.對每個天線對執行射線跟蹤算法,算法中繞射采用Berg遞歸模型,每條射線路徑最多包含4個射線段.最后對所有的天線對計算結果進行統計,得到所提模型的參數分析結果.

3.1 時延擴展

均方根時延擴展表示如下:

其中,

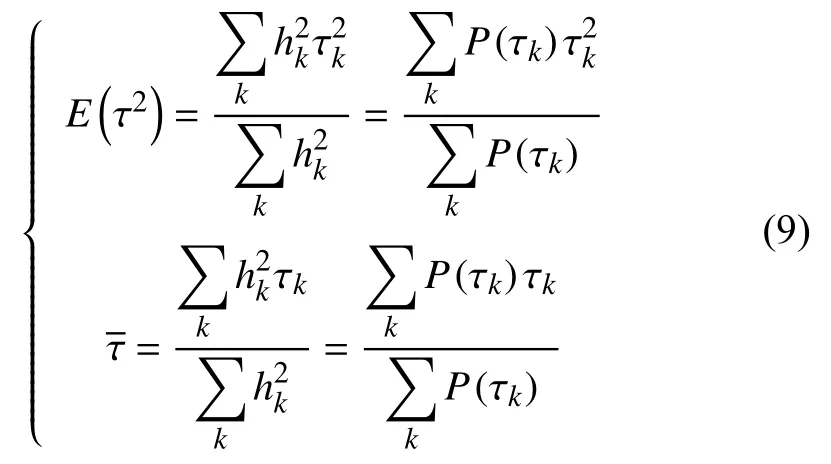
上式中,p( τk)為功率時延譜.在不同載波頻率下,時延擴展的對數值 lo g10(στ)如表1所示.可以看出,在LoS場景下,時延擴展受載波頻率影響很小,而在NLoS場景下,隨著載波頻率的增加,時延擴展降低.

表1 不同載波頻率時延擴展 (單位:dB)

3.2 散射簇到天線距離分布

3.3 算法復雜度分析

傳統射線跟蹤算法的實用性不高,主要體現兩方面:一是實際場景地圖的獲取困難,二是繞射和散射系數的計算復雜.所提方法從上述兩方面對算法的計算復雜度進行優化.

針對實際場景地圖獲取困難的問題,采用簡化的馬德里格地圖來替代,已有文獻證明馬德里格能夠反映大部分場景的信道特性[26].

針對繞射系數的計算,用Berg遞歸模型代替傳統的UTD理論,可以在不影響算法精度的前提下,大大降低算法運行時間.在圖8所示的NLoS鏈路場景下,圖10分別給出Berg遞歸模型計算得到的功率時延譜(藍色方框)和UTD理論得到的功率時延譜(紅色上三角).圖中僅給出衰減小于210 dB的多徑,衰減更大的徑忽略不計.可以看出,UTD的多徑數量高于Berg遞歸模型,這是因為前者的繞射范圍更大.但是兩者的強徑(衰減小于180 dB)基本吻合,UTD得到更多的弱徑 (衰減大于 180 dB),這對整體信道特性影響不大.采用相同配置的PC進行計算,Berg遞歸模型所需的時間為 3.808 s,UTD 所需的時間為 10.499 s,時間差別主要是由于徑的數量不同和迭代計算的方法不同.

圖9 散射簇到天線距離概率分布

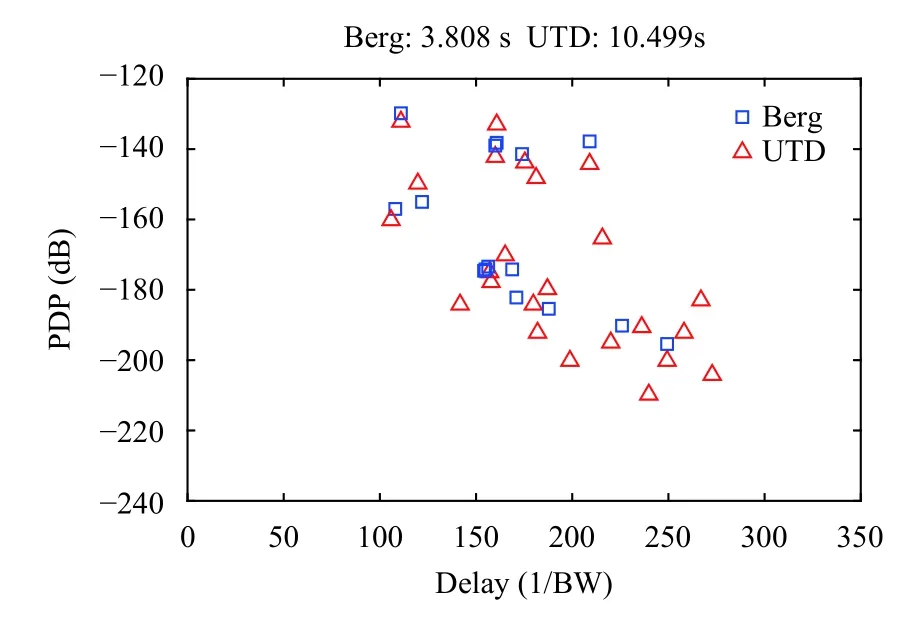
圖10 Berg 遞歸模型和 UTD 的性能對比

4 結語

論文通過分析傳統MIMO信道模型應用于大規模MIMO信道時存在的問題,基于非平面波的假設理論,建立了非平面波假設的大規模MIMO信道模型框架;實現了基于馬德里格地圖的射線跟蹤算法.在此基礎上,對大規模MIMO信道模型的時延擴展、天線到散射簇距離等模型參數進行了計算,并給出統計分布的結果.上述分析結果表明本文所題模型能夠反映大規模MIMO的主要信道特征,對基于大規模MIMO的系統開發具有重要的指導意義.