設置黏滯阻尼器的斜拉索參數振動模型及控制分析

汪峰 彭章 劉章軍

摘要：為了掌握黏滯阻尼器對斜拉索參數振動的抑振效果，考慮拉索幾何非線性、傾角以及橋塔和加勁梁的協同振動影響，建立了黏滯阻尼器一拉索一塔梁耦合體系的參數振動模型，推導了黏滯阻尼器作用下斜拉索的運動方程組，提出了控制拉索參數振動的阻尼器阻尼系數計算公式，并與傳統單索模型對比，分析了塔梁協同作用對拉索固有頻率的影響水平;編制計算程序比較了斜拉索安裝阻尼器前后的振動位移時程特征，研究了三種典型索梁頻率比下阻尼器的阻尼系數、安裝位置對拉索參數振動的影響。結果表明：塔梁協同作用對拉索固有頻率的影響水平與索力、索長密切相關，索力越小，索長越長，塔梁協同作用的影響率也越大。安裝了黏滯阻尼器后，斜拉索的振動位移呈非線性衰減趨勢;隨著阻尼系數的增大，拉索的最大振幅逐漸減小，但其振幅衰減率呈現先增加后降低的趨勢，系統存在一個最優阻尼系數;阻尼器安裝位置距離索梁錨固端越遠，拉索振幅越小，存在一個衰減率為零的臨界安裝位置，當阻尼器安裝位置超過臨界位置時，振幅不能持續衰減，阻尼器的抑振效率降低。

關鍵詞：斜拉索;黏滯阻尼器;耦合模型;協同作用;參數振動控制

中圖分類號：U448. 27;U441+.3

文獻標志碼：A

文章編號：1004-4523 （2019） 06-0977-09

D0I：10. 16 385/j. cnki. issn. 1004-4523. 2019. 06. 006

引言

斜拉橋是由斜拉索、橋塔和加勁梁構成的組合結構，因其跨越能力大，質量輕、造型美觀，已成為大跨度橋梁的首選。但斜拉橋的索梁體系自阻尼小，在車輛、風雨、地震等復雜環境載荷作用下，拉索極易產生低頻、高幅、持續的振動[1]。斜拉索的強烈振動會引起索梁錨固區出現疲勞裂紋，拉索保護層脫落等病害[2]，影響橋梁結構的使用和安全性能。近年來，通過對某些服役期大跨度斜拉橋的振動觀測表明[3]，在微風細雨時某些拉索會發生1m以上的振動幅值，普遍認為這是由橋塔或橋面激勵引起的參數振動，不同于強風雨激振。

目前，斜拉索振動控制多采用工作機理簡單、造價低、易于維護的外置式黏滯阻尼器。針對斜拉索黏滯阻尼器的抑振機理和效果問題，國內外學者開展了廣泛研究。巫生平等[4]結合某斜拉橋有限元模型，研究了不同阻尼器布設位置對橋梁位移、內力的影響，提出了利用最小二乘回歸分析得到最優阻尼參數的方法。周海俊等[5]構建了拉索一阻尼器一彈簧系統，推導了系統的運動方程及特征頻率方程，求出兩種不同工況下系統阻尼比和頻率的近似解析解，研究了系統最大模態阻尼比和拉索振動頻率的變化規律。段元鋒等[6]基于斜拉索一阻尼器系統模型，通過變量分離、參數統計等方法，提出了可近似獨立衡量各參數影響的黏滯阻尼器實用設計方法。陳文禮等[7]建立了阻尼器一水平索耦合振動模型及其運動方程，以兩根不同長度的拉索為對象，研究了拉索垂度對阻尼器控制效果的影響，發現阻尼器對小垂度拉索的控制效果更好。龔平等[8]將拉索簡化為彈簧單元，建立了斜拉橋動力學模型，研究了拉索對全橋豎向振動頻率的影響。

上述研究為斜拉索的振動控制提供了堅實的理論基礎，但建立斜拉索一阻尼器體系力學模型時，大部分研究忽略了橋塔和加勁梁的協同振動影響，這種簡化處理是否能滿足拉索抑振設計的精度要求，尚未有明確的結論。因此，為了更加準確的掌握黏滯阻尼器的參數設置對拉索防振的影響，結合文獻[9-10]的研究成果，考慮塔梁協同作用，引入黏滯阻尼器，構建斜拉橋塔一索一梁結構體系的耦合參數振動模型，提出控制拉索參數振動的最優黏滯阻尼器系數計算公式，分析塔梁協同作用對拉索固有頻率的影響水平，比較斜拉索受控前后的拉索振動位移特征。研究黏滯阻尼器的阻尼系數、安裝位置對拉索參數振動的影響規律，研究結果為大跨度斜拉橋減振設計提供理論依據。

1 阻尼器一拉索一塔梁耦合振動模型

1.1 基本假定

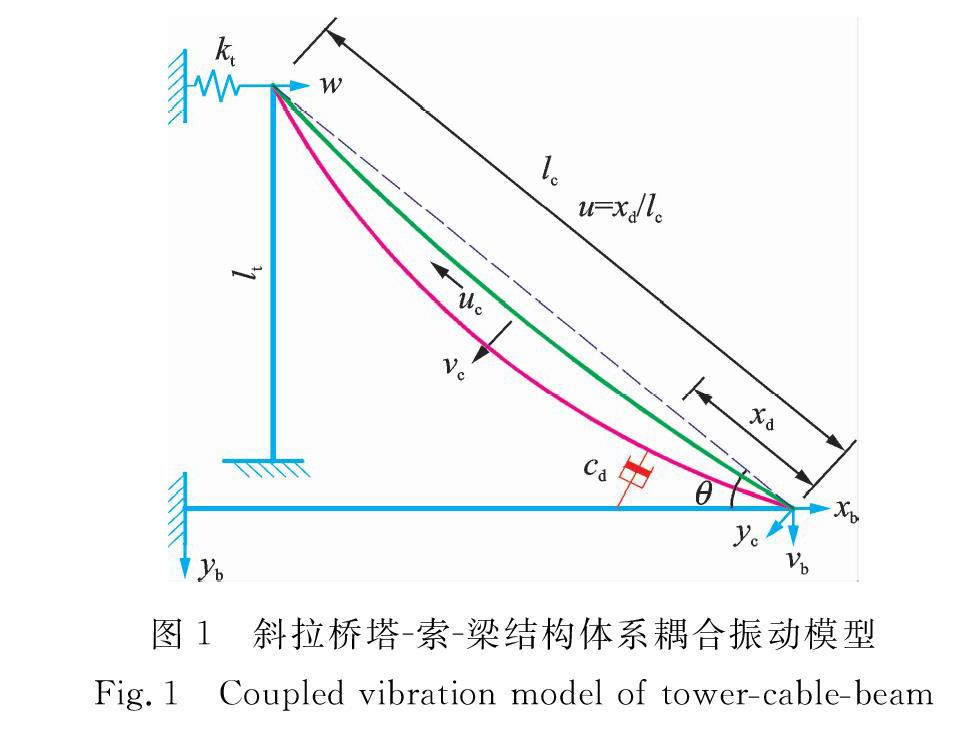
為了突出問題本質，作如下假設：（1）拉索自重沿索長均勻分布，忽略重力垂度以及熱脹冷縮引起的拉索質量重分布;（2）拉索本構關系符合胡克定律，忽略拉索抗彎剛度、抗扭剛度和抗剪剛度的影響;（3）阻尼器為線性黏滯阻尼器。考慮橋塔和加勁梁的協同振動影響，建立設置黏滯阻尼器的斜拉橋拉索一塔梁耦合體系的振動模型，如圖1所示。

現代大跨度斜拉橋多采用密索體系，橋塔高度已達數百米，并受到多根拉索約束，塔梁結合處常采取固結方式來減小橋塔的內力和加勁梁的軸向拉力。因此，將橋塔視為一端固結，另一端與拉索鉸接的Bernoulli-Euler梁。為了考慮其他拉索對橋塔的扶正作用，用剛度為kt的彈簧作為橋塔頂端的外力邊界，并假定塔頂橫向位移為W（t）。橋梁在地震、風荷載以及車輛荷載等作用時，加勁梁會將這些荷載傳遞至索塔，再通過索塔傳至地基，加勁梁在斜拉索的各點支承作用下，像多跨彈性支承的連續梁，在外激勵下易產生豎向位移。因此，將加勁梁視為Bernoulli-Euler梁，一端固結邊界，另一端與拉索鉸接，其豎向振動位移為ub。拉索與橋塔、加勁梁鉸接，uc和ue分別為拉索的縱向和橫向的振動位移。黏滯阻尼器的兩端分別與拉索、加勁梁連接，它到索梁錨固點的距離為xd，阻尼系數為Cd，安裝位置參數u=xd/ιc。各構件參數定義如表1所示。

1.2 設置阻尼器的斜拉索振動控制方程

為計入拉索重力弦向分力的影響，設定斜拉索靜態線形為高精度拋物線，其線形方程為

式中 ye為拉索垂度，H為索力水平分力。

基于達朗貝爾原理，拉索做橫向振動時面內運動微分方程為 式中 h為斜拉索動張力的水平分力，d為拉索的跨中垂度，δ為狄克拉函數，Fd為黏滯阻尼器的阻尼力，其大小為阻尼系數乘以拉索運動速度，表達式為：Fd （t） =Cd uc（xd，t）。 限于篇幅，斜拉索水平動張力h推導過程可參考文獻[9]，其表達式如下

研究表明，斜拉索振動時的一階模態響應占總響應的比例較大[11]。因此，本文僅考慮拉索的一階振動模態，斜拉索橫向振動位移為

式中 拉索振型

，Ve表示拉索跨中橫向振幅。由于式（4）包含了橋塔和加勁梁的振動引起的拉索位移，因此耦合振動模型可考慮橋塔和加勁梁的協同作用引起結構體系的動力學效應。

加勁梁簡化為Bernoulli-Euler懸臂梁，其運動偏微分方程為 式中 軸向力N=（H+h）cosθ+Fd sinθ，將加勁梁位移ub分離變量，且僅考慮加勁梁一階振動模態

ub（xb，t）=Vb（t）φb（xb）

（6）式中 加勁梁振型[12-14]為φb（xb）=A1sir（βbxb）+A2 cos（βbxb）+A3 sinh（βbxb）+A4 cosh（βbxb），依據文獻[10]可對A1，A2，A3，A4，βb等參數進行計算。

定義橋塔橫向位移為ut（z，t）=φt（z）·W（t），其動力運動方程如下式

式中Mt*，Ct*，Kt*，Pt*分別表示橋塔的廣義質量、阻尼、剛度和外荷載。

最后采用伽遼金方法，分別對拉索、加勁梁和橋塔的振動方程進行模態截斷，可獲得橋塔一索一梁耦合體系的振動方程組，為：

由于上述方程組之間存在高次非線性項，使得索梁模型較為復雜，它耦合了橋塔和加勁梁的振動。分別定義橋塔、拉索、加勁梁的固有頻率為Wl，w2，w3，則橋塔振動頻率：

;拉索振動頻率：

;橋面頻率：

。黏滯阻尼器給拉索附加的阻尼比如下式所示

附加阻尼比系數會影響斜拉索的抑振效果。當阻尼系數過小時，阻尼器無法有效抑制拉索的振動;當阻尼系數過大時，阻尼器相當于一個固定約束，將長索轉換為兩根短索自由振動，并不能起到有效地減振耗能作用。因此，存在一個最優的阻尼系數，使阻尼器的控制效果最好。由圖1知，u為阻尼器到索梁錨固點的距離Xd與拉索弦向長度ιc的比值。根據文獻[7]建議的被動線性黏滯阻尼器對拉索的最優附加模態阻尼比為ξb=0. 5u。結合以往研究[15-16]，將ξb代入式（11）可得最優黏滯阻尼器系數的表達式由式（12）可知，最優黏滯阻尼器系數Cd與拉索本身的材料參數、固有頻率以及阻尼器安裝位置相關。與傳統單索模型推導的阻尼器阻尼系數相比，該模型可考慮橋塔和加勁梁對斜拉索協同振動的影響。

2 拉索參數振動控制分析

2.1 塔梁協同作用對拉索固有頻率的影響

通過上述斜拉索的運動方程求解，可得拉索一階固有頻率w2的表達式如下式所示

為了便于對比分析，基于傳統單索模型[16-17]，推導拉索一階固有頻率w0，如下式所示式中

對比w2和w0。表達式可知，引入加勁梁、橋塔對斜拉索的協同作用后，斜拉索內力及邊界條件發生變化，一階固有頻率出現多個高次非線性項，在某種程度上影響斜拉索的振動特性。為了研究塔梁協同作用對拉索振動的具體影響，取某斜拉橋的一組斜拉索為算例，具體參數如下：斜拉索單位質量mc=80. 72 kg/m，兩端錨固點之間的距離ιe=292. 57m，彈性模量Ee=2.1×1011 Pa，截面積Ae=0. 01022 m2，傾角0= 30°，重力加速度g=9.8 m/s2，索力H取值為4×l04_2×l05 N，可得上述兩種模型的拉索固有頻率與索力關系曲線，如圖2所示。

由圖2可知，隨著斜拉索索力的增大，拉索的固有頻率呈現非線性減小趨勢。索力在4×l04_2 0×l04 N之間變化時，單索模型的頻率w0。明顯大于耦合模型頻率w2，兩者最大比值可達1.57。但隨著索力的增大，斜拉索逐漸張緊，w0與w2曲線的差值逐漸減小，最后趨于重合，塔梁協同作用對張緊拉索的固有頻率影響變小。

保持索力H=20×l04 N不變，改變索長ιe值，可得兩種模型的拉索固有頻率與索長的關系曲線，如圖3所示。

由圖3可知，隨著索長增加，拉索固有頻率同樣呈現非線性減小趨勢。索力為2 0×l04 N的拉索，索長在25-400 m之間變化時，單索模型的頻率w0大于耦合模型的頻率w2，且隨著索長的增大，w0與w2的差值也逐漸增大。說明塔梁的協同作用對長索的影響較大，兩者最大比值為1. 02。與索力相比，索長對拉索固有頻率的影響較小。

對部分斜拉索而言，單索模型精度與本文的耦合模型相當。但在研究超長斜拉索的振動時，把所有拉索簡化為單索模型無法反映拉索的真實情況。與單索模型對比，表2給出了不同長度的斜拉索在不同索力下，塔梁協同作用對固有頻率的影響水平。

由表2可知，拉索索長為50 m，索力為40 kN時，塔梁協同作用對拉索固有頻率的影響率為-0. 87%，當索長增加到250 m時，影響水平變為-24.77%。但索力增大到200 kN時，其影響水平降低為-0. 03%。由此可見，斜拉索越長，索力越小時，塔梁協同作用的影響愈加明顯。而索長越短，索力越大時，塔梁協同作用的影響越弱。因此，斜拉索抑振設計時建議考慮塔梁協同作用的影響。

2.2 黏滯阻尼器的控制效果分析

采用四階龍格庫塔法，編制程序分析斜拉索受控前后的拉索振動位移特征，研究阻尼器的阻尼系數、安裝位置、對拉索參數振動的影響。拉索計算參數如表3所示。

由表3參數可計算橋塔、斜拉索和加勁梁的一階固有頻率分別為：w1=19.2 rad/s，w2=8. 864rad/s，w3 =19.2 rad/s。為了研究阻尼器一斜拉索一塔梁結構體系在w1：w2：w3 =2：1：2的頻率比下，安裝阻尼器前后的斜拉索位移變化，橋塔、拉索和加勁梁的初始位移均為0. Ol m。斜拉索位移時程如圖4所示。

由圖4（a）可知，斜拉索處于未安裝阻尼器的無控狀態時，拉索由初始位置開始振動，其振幅逐漸增大，在較短時間內達到響應峰值，幅值為1.19 m，到500 s時拉索振動趨于穩定，振幅幾乎沒有衰減。由圖4（b）可知，斜拉索安裝了黏滯阻尼器后，變成有控狀態，拉索同樣在較短時間內達到響應峰值1. 19m，但隨著時間的推移，拉索振幅衰減明顯，到500 s時，振幅降為0. 728 m。

拉索發生參數振動時，由于附加阻尼力的存在，其振動幅值逐漸衰減。為了更進一步揭示黏滯阻尼器的抑振效果，引入振幅衰減率λ，其計算公式為式中 A為某時刻未安裝阻尼器的無控斜拉索最大振幅，Ao表示有控狀態時斜拉索的最大振幅。利用公式（15）可計算受控的斜拉索在500 s時振幅衰減率約為39%。

2.3 黏滯阻尼器阻尼系數的影響

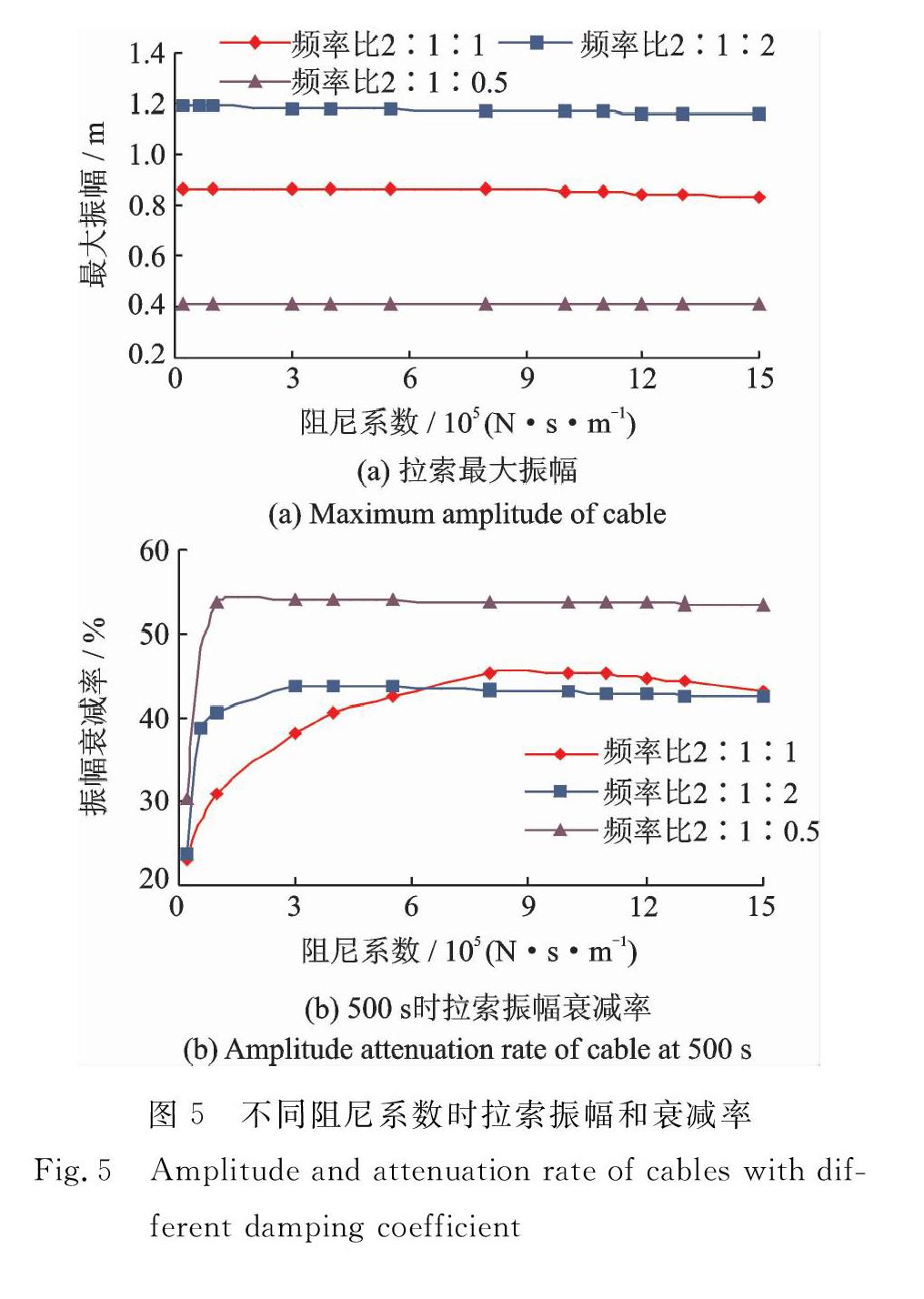
工程實踐中，考慮阻尼器安裝可行性和橋梁景觀性，黏滯阻尼器的安裝位置一般靠近索梁錨固端。取安裝位置參數u=. Ol，通過改變表3中塔、梁結構參數以及黏滯阻尼系數Cd的取值，可獲得索梁頻率比分別為1：2，1：1，1：0.5的3種典型參數振動匹配關系，分析阻尼系數對斜拉索的振動影響。不同頻率比時，黏滯阻尼器系數與拉索振幅、衰減率的關系曲線如圖5所示。

由圖5（a）可知，在3種典型索梁頻率比時，隨著阻尼系數的增大，斜拉索最大振幅均呈輕微的非線性衰減趨勢，且衰減過程較慢。由圖5（b）可知，隨著阻尼系數的增大，拉索振幅衰減率呈現先增大后減小的趨勢。振幅衰減率明顯存在一個峰值，即有一個臨界最優阻尼系數Cd'。當拉索阻尼系數CdCd'時，隨著阻尼系數的增大，雖然拉索振幅持續減小，但是振幅衰減率呈現緩慢減小的趨勢，且阻尼器的控制效果并沒有明顯提高。因此，建議阻尼系數設計取值在某一合理范圍內，既能滿足經濟、技術性，也能達到最大的控制效果。

同時，不同頻率比下拉索的臨界阻尼系數并不相同。當索梁頻率比為1：2和1：0.5時，阻尼系數在2×l05-3×l05 N·s/m時的控制效果最佳，而當索梁頻率比為1：1時，阻尼系數取值為8×l05-1.1×l06 N·s/m時，拉索振幅的控制效果最佳。為了最大限度地控制拉索在不同頻率比下的振動，阻尼器的阻尼系數應取上述較大值8×l05-1.1×106 N·s/m。而由式（12）可得，最優阻尼系數為1. 06×l06 N·s/m，與分析結果吻合較好。因此，黏滯阻尼器的最優阻尼系數公式考慮了橋塔、加勁梁與斜拉索的協同振動影響，同時計算方法準確便捷，工程人員可根據實際情況估算阻尼器阻尼系數。

2.4 黏滯阻尼器安裝位置影響

為了研究阻尼器的安裝位置u對拉索振幅和振幅衰減率的影響，阻尼器的阻尼系數取值1. 06×106 N·s/m。不同阻尼器位置參數u與最大振幅、衰減率的關系，如圖6所示。

由圖6可知，隨著阻尼器安裝位置參數u的增大，即阻尼器位置逐漸靠近斜拉索跨中，遠離索梁錨固端時，拉索最大振幅和500 s時振幅衰減率呈非線性減小趨勢。阻尼器距離索梁錨固端越遠，拉索的最大振幅越小，但振幅衰減率也越小。系統存在一個衰減率為零的臨界安裝位置u'，當安裝位置u>u'時，拉索的振幅衰減率降至負值，此時拉索的振幅隨著時間的推移有升高的趨勢。斜拉索在不同頻率比時，阻尼器的臨界安裝位置并不相同，索梁頻率比為1：0.5的超諧波共振時的u'值最大，1：1的主參數共振次之，1：2的主參數共振時的u'值最小。因此，為了有效控制拉索不同模式的振動，建議黏滯阻尼器的安裝位置u不宜超過0. 05。

有趣的是，當阻尼器的安裝位移在[O O.04]之間，頻率比為2：1：1和2：1：2時，斜拉索振幅衰減曲線較為近似，表明阻尼器對兩種共振的振幅抑制效果相近。分析其原因是頻率比為2：1：2下，斜拉索發生主參數共振，當頻率比為2：1：1時，拉索會發生主共振，都屬于亞諧波共振，其振動形式機理具有一定的相似性。這兩種共振模式下斜拉索都符合“拍”形特征，但是最大振幅不同。而頻率比2：1：0.5時，斜拉索的振動屬于超諧波共振，其振幅衰減率大于亞諧波共振。

3 結 論

本文建立了阻尼器一斜拉索一塔梁組合結構體系的耦合參數振動模型，分析了塔梁協同作用對拉索固有頻率的影響水平，比較了斜拉索受控前后的拉索振動位移特征，研究了黏滯阻尼器的阻尼系數、安裝位置對拉索參數振動的影響，得到如下結論：

（1）塔梁協同作用對斜拉索固有頻率的影響與拉索索力、索長密切相關。斜拉索越長，索力越小，塔梁協同作用的影響越強。反之，其影響越弱。斜拉索抑振設計中，建議考慮塔梁協同作用的影響。

（2）相比于未設置黏滯阻尼器的斜拉索，設置黏滯阻尼器的斜拉索的最大振幅更小，且振幅呈明顯的非線性衰減，黏滯阻尼器可有效抑制斜拉索的參數振動。

（3）隨著阻尼系數的增大，拉索的振幅衰減率呈先增大后趨于減小的趨勢。黏滯阻尼器存在一個臨界最優阻尼系數Cd'，當阻尼器的阻尼系數超過臨界阻尼后，斜拉索的振幅衰減率呈減小趨勢，抑振效果的提高并不明顯。工程實際時，在滿足經濟性、技術性的同時，阻尼器的阻尼系數應控制在某一合理范圍內。

（4）阻尼器安裝位置距離索梁錨固端的距離越大，拉索最大振幅和振幅衰減率越小。黏滯阻尼器也存在一個衰減率為零的臨界安裝位置u'，當安裝位置超過u'后，斜拉索的振幅衰減率為負值，抑振效果較差。在工程實際中，建議黏滯阻尼器的安裝位置u不宜超過0. 05。

（5）考慮斜拉橋、橋塔和加勁梁三者協同振動，黏滯阻尼器一拉索一梁結構體系的最優阻尼系數的計算方法準確便捷，工程人員可以根據實際情況計算黏滯阻尼器需要滿足的阻尼系數。

參考文獻：

[1] Wu Q， Takahashi K， Nakamura S. Non-linear re-sponse of cables subjected to periodic support excita-tion considering cable loosening[J]. Journal of Soundand Vibration，2004，27（1/2）：453-463.

[2] Lilien J L， Pinto Da Costa A. Vibration amplitudescaused by parametric excitation of cable stayed struc-tures[J]. Journal of Sound and Vibration，1994，174（1）：69-90.

[3] Yamaguchi H， Fujino Y. Stayed Cable Dynamics andIts Vibration Control[M]. Bridge Aerodynamics，Balkema Rotterdam，The Netherlands，1998： 235-253.

[4] 巫生平，張 超，房貞政，斜拉橋黏滯阻尼器設計方案及參數回歸分析[J].橋梁建設，2014，44（05）：21-26.

Wu Shengping， Zhang Chao， Fang Zhenzheng. Designschemes and parameter regression analysis of viscousdampers for cable-stayed bridge[J]. Bridge Construc-tion，2014，44（05）：21-26.

[5] 周海俊，丁 煒，孫利民，拉索一阻尼器一彈簧系統的阻尼特性分析[J].工程力學，2014，31（01）：79-84.

Zhou Haijun，Ding Wei，Sun Li-min. Damping of tautcable with a damper and spring[J]. Engineering Me-chanics，2014，31（01）：79-84.

[6] 段元鋒，李 頻，周仙通，等，斜拉索外置式黏滯阻尼器實用設計方法[J].中國公路學報，2015，（11）：46-511+59.

Duan Yuanfeng， Li Pin， Zhou Xiantong， et al. Practi-cal design method for external viscous damper of staycable[ J]. China Journal of Highway and Transport，2015，（11）：46-51-1- 59.

[7] 陳文禮，李 惠，黏滯阻尼器對拉索參數振動的控制分析[J].地震工程與工程振動，2007，（02）：137-144.

Chen Wenli， Li Hui. Passive control for parametric vi-bration of cables using viscous fluid dampers[J].Earthquake Engineering Vibration， 2007， （02）： 137-144.

[8] 壟 平，蘇瀟陽，蔡向陽，等，拉索對斜拉橋豎向頻率的影響研究[J].振動工程學報，2018，31（6）：957-965.

GONG Ping，SU Xiaoyang，CAI Xiangyang，et al. Theinfluence of cables on vertical frequency of cable-stayedbridge[J]. Journal of Vibration Engineering，2018，31（6）：957-965.

[9] 汪 峰，陳福清，文曉旭，等，考慮溫度影響的斜拉索參數振動模型及響應分析[J].重慶交通大學學報（自然科學版），2016，35（2）：1-6.

Wang Feng， Chen Fuqing， Wen Xiaoxu， et al. Analy-SiS of cable parametric vibration model and responsewith consideration of temperature effect[J]. Journal ofChongqing Jiaotong University （Natural Science），2016.35（2）： 1-6.

[10]汪 峰，文曉旭，劉章軍，斜拉橋塔一索一梁耦合參數振動模型及響應分析[J].固體力學學報，2015，36 （5）：446-452.

Wang Feng， Wen Xiaoxu， Liu Zhangjun. Coupled vi-bration model for tower-cable-deck of long-span cable-stayed bridge and its response analysis[J]. ChineseJournal of Solid Mechanics，2015，36（5）：446-452.

[11]楊詠漪，陳克堅，大跨度鐵路斜拉橋斜拉索參數振動分析[J].鐵道工程學報，2012 ，169 （10）：60-65.

Yang Yongyi， Chen Kejian. Research on parametricoscillation of cables for long span railway cable-stayedbridge[J]. Journal of Railway Engineering Society，2012， 169（10）： 60-65.

[12]康厚軍，趙躍宇，蔣麗忠，參數振動和強迫振動激勵下超長拉索的面內非線性振動[J].中南大學學報（自然科學版），2011，42（8）：2439-2445.

Kang Houjun， Zhao Yueyu， Jiang Lizhong. In- planenonlinear vibration of super long stay cables under par-ametric and forced excitations[J]. Journal of CentralSouth University （Science and Technology），2011，42（8）： 2439-2445.

[13] Wang T M， Nettleton R H， Keita B.Natural frequen-cies for out-of-plane vibrations of continuous curvedbeams[J]. Journal of Sound and Vibration，1980， 68（3）： 427-436

[14] Gattulli V， Martinelli L， Perotti F， et al. Nonlinearoscillations of cables under harmonic loading using an-alytical and finite element models[J]. Computer Meth-ods in Applied Mechanics and Engineering， 2004， 193（1/2）：69-85

[15] Pacheco B M， Fujino Y， Sulekh A. Estimation curvefor modal damping in stay cables with viscous damper[J]. Journal of Structural Engineering，1993，119 （6）：1961-1978.

[16]陳丕華，大跨斜拉橋拉索的參數振動及其控制[D].長沙：湖南大學，2009.

Chen Pihua. Parametric vibration of cable and its con-trol in long-span cable-stayed bridge[D]. Changsha：Hunan University，2009.

[17]王 波，大跨斜拉橋拉索局部振動特性及其影響研究[D].武漢：華中科技大學，2008.

Wang Bo. Characteristic and influence of local cable vi-bration on long-span cable-stayed bridge[D]. Wuhan：Huazhong University of Science and Technology，2008.