鐵路自復位高墩的高階模態貢獻研究

杜騫 夏修身 陳興沖 孫學先

摘要：針對高階模態對自復位橋墩的影響，以某鐵路58 m高墩為例，基于OpenSEES建立自復位高墩地震反應模型。輸入近場地震動強震記錄，通過增量動力分析得出了墩身塑性鉸的形成及發展規律。基于模態分解法討論了前3階模態對墩身彎矩和墩頂位移的影響，引入一種定量指標評價了各階模態反應的貢獻。結果表明：在近場地震作用下，自復位高墩墩底提離后只會減小第1階模態響應對墩身的作用，使墩底不出現塑性鉸;受高階模態地震響應的影響，墩身中部仍會出現塑性鉸區，墩底提離不能消除高階模態的作用。

關鍵詞：自復位高墩;高階模態;振型貢獻率;地震反應

中圖分類號：U24

文獻標志碼：A

文章編號：1004-4523 （2019） 06-1003-08

DOI：10. 16 385/j. cnki. issn. 1004-4523. 2019. 06. 009

引言

高墩橋梁廣泛應用于中國西部高烈度山區。為了實現強震下橋墩及基礎基本無損的目標，文獻[1]提出了一種鐵路新型自復位高墩，分析了高墩隔震效果，結果表明鐵路橋梁采用自復位高墩較墩頂設置減隔震裝置隔震效果明顯。文獻[2]對鐵路橋梁自復位高墩不同數值模型進行了地震反應研究，提出了一種可靠的兩彈簧模型和提離剛度的取值方法。文獻[3-4]分析了墩底限位普通鋼筋和預應力筋的預應力效應對鐵路橋梁自復位高墩地震反應的影響。文獻[5]考查了近場地震動對自復位高墩的影響，結果表明近場地震動高墩的搖擺反應明顯大于普通地震動。以上研究成果均表明，墩底提離可避免墩底出現塑性鉸區，但對強震下墩中是否出現塑性鉸沒有關注，更沒有探討高階模態效應對自復位高墩的影響。

國內外學者對傳統高墩中的高階模態作用開展了諸多研究。文獻[6]指出受高階模態的影響，高墩墩頂最大位移和墩底最大曲率出現的時刻不同步。文獻[7]通過墩身曲率包絡和Pushover曲線分布驗證了墩中塑性鉸由第2階振型控制。文獻[8]通過對墩身塑性鉸產生、發展規律的分析，得出普通高墩在高階模態作用下，墩身中部區域出現塑性鉸。以上研究說明結構地震反應存在高階模態的影響，但各階模態對結構地震反應的貢獻無定量分析。在房屋建筑中，最早采用振型分解法對工業廠房、高層及超高層樓房進行了高階振型影響的定量分析[9-10]。文獻[11]引入振型分解法對自復位橋墩高階振型影響進行了定量分析，但只考察了墩底內力和墩頂位移影響。文獻[12]采用瞬時模態分析法，通過研究延性位移譜值隨墩底曲率增加的變化規律來反映瞬時高階模態的貢獻程度，其研究方法可供本文借鑒。

為了研究自復位隔震高墩中高階振型的影響，以某鐵路橋58 m高墩為例，基于OpenSEES（ OpenSystem for Earthquake Engineering Simulation）建立了數值分析模型。由于近場地震動對自復位高墩墩頂位移影響顯著[5]，本文采用增量動力（IDA）分析方法考察近場地震動對自復位高墩地震反應的影響，引入模態分解法近似定量分析了前3階模態對結構地震反應的貢獻。研究結果可為鐵路新型自復位高墩設計及應用提供理論依據。

1 各階模態動力響應的度量方法

1.1 各階模態貢獻的計算方法

本文采用模態分解法[10]對鐵路高墩的各階模態貢獻進行分析。模態分解法在線性系統中成立，因此進行非線性分析的結果是一種近似解。

1.1.1 各階模態內力計算

結構各階模態引起的結構內力，包括剪力和彎矩，可以根據對結構非線性時程計算得到的等效地震荷載進行模態分解而求得。根據結構動力學[13]模態分析的相關知識，首先引入非線性多自由度結構第規階模態的等效地震靜力frn（t），表達式為

fr，n（t）-Sn·an（t）

（1）式中 an（t）為與線性結構中的偽加速度An（t）相對應的非線性系統中第n階模態的偽加速度，sn是第n階模態等效地震荷載的空間分布向量

sn=Fn·mφ

（2）式中 Fn為振型參與系數，m為結構質量矩陣，φn為結構的第n階振型。

假定疊加原理對搖擺自復位結構仍然適用，則結構t時刻總的等效地震靜力fr（t）等于t時刻各階等效地震靜力之和，即

利用振型的正交性，將式（3）左右兩側左乘φTn經整理得

式中Mn為第n階模態的廣義質量。

根據非線性時程計算的結構剪力結果可以得到時刻t結構的等效地震靜力fr（t），由式（4）可以得到an（t），式（1）計算各階模態的等效地震靜力，進而計算各個時刻各階模態對應的剪力及彎矩等內力。

1.1.2 各階模態位移計算

為計算各階模態位移，需要引入與第n階模態單自由度線性系統位移響應Dn（t）相對應的第n階模態單自由度非線性系統等效位移響應δ（t）。則第n階模態的位移向量un（t）可以表示為

un（t）=Fn·φn·δn（t）

（5）

利用疊加原理，結構總的位移向量可以表達為

利用振型的正交性，式（6）左右兩側左乘φTn，經整理可得第n階模態單自由度非線性系統的等效位移響應為

在得到δ（t）之后，根據式（5）便可以得到各個時刻各階模態對應的結構位移。

1.2 各階模態貢獻的定量評價

采用模態分解法求出各階模態對應的內力、位移后，為描述各階模態對結構響應的貢獻大小，引入一種評判指標QM1[l0]，如下式

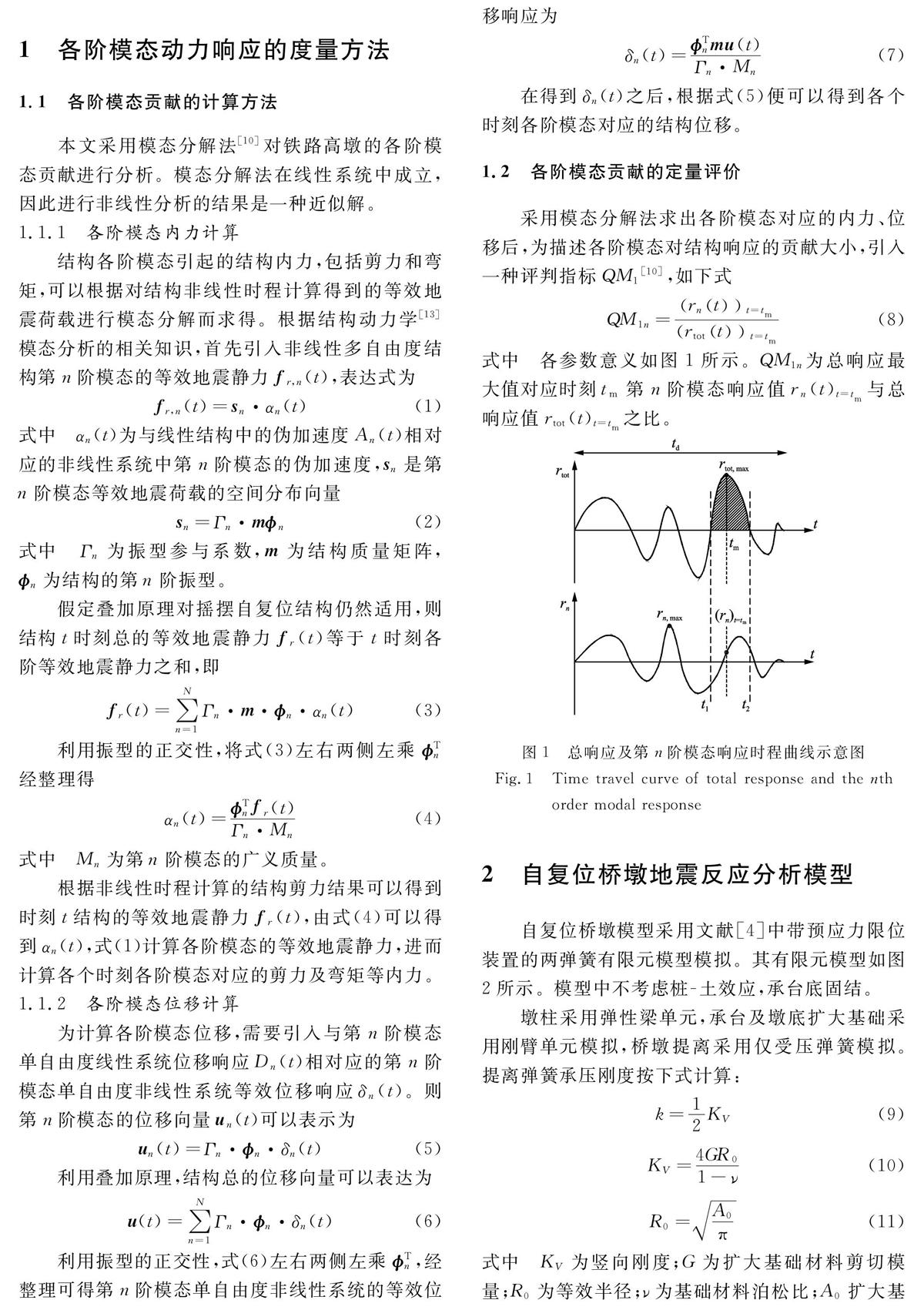
式中 各參數意義如圖1所示。QM1n為總響應最大值對應時刻tm第n階模態響應值rn（t）t=tm與總響應值rtot（t）t=tm之比。

2 自復位橋墩地震反應分析模型

自復位橋墩模型采用文獻[4]中帶預應力限位裝置的兩彈簧有限元模型模擬。其有限元模型如圖2所示。模型中不考慮樁一土效應，承臺底固結。

墩柱采用彈性梁單元，承臺及墩底擴大基礎采用剛臂單元模擬，橋墩提離采用僅受壓彈簧模擬。提離彈簧承壓剛度按下式計算：式中 Kv為豎向剛度;G為擴大基礎材料剪切模量;R0為等效半徑;V為基礎材料泊松比;A0擴大基礎截面積。提離彈簧本構模型如圖3所示。

預應力筋本構模型按照理想雙線性近似模擬[4]，不考慮預應力筋受壓（如圖4所示）。預應力鋼筋單元的初始剛度為式中 E為預應力鋼筋的彈性模量;A為預應力鋼筋的橫截面積;L為預應力鋼筋的非約 長度。

3 算例分析

3.1 工程背景

某單線鐵路32 m簡支梁直線橋，下部采用群樁基礎空心圓端型橋墩（如圖5所示）。橋址設計地震動峰值加速度0. 20g，Ⅱ類場地，特征周期0. 45 s。以該橋1 8號58 m高墩作為研究對象，墩頂橫橋向6.3 m，順橋向4.2 m;墩底橫橋向9.1 m，順橋向7.Om;壁厚1.12 m，內坡1：90，外坡1： 40;縱筋配筋率1.O%，體積配箍率0.4%，墩身采用C35混凝土。

傳統結構形式（如圖6（a）所示）順橋向1階周期為0. 95 s。當設計為自復位橋墩時，墩底擴大基礎尺寸為10 m×12 m×2m，采用C30混凝土（如圖6（b）所示）。

3.2 地震動輸入

從美國太平洋強震數據庫選取1994年美國Northridge強震記錄作為輸入地震動（如圖7所示），通過增量動力分析法進行順橋向非線性時程分析。

3.3 有限元模型建立

基于OpenSEES建立帶預應力筋的自復位隔震橋墩地震反應分析模型。橋墩與剛臂均采用彈性梁柱單元element elasticBeamColumn，橋墩共劃分2 6個單元，27個節點，其中剛臂的剛度取橋墩單元最大剛度的100倍。提離彈簧單元采用element zeroLength模擬，且采用彈性非受拉材料unlaxialMaterial ENT，提離彈簧剛度k由式（9）-（1 1）計算取2.1×l08 kN/m。預應力鋼筋采用桁梁單元模擬，其材料本構特性通過umaxialMaterialElasticPP來實現（如圖8所示），初始預加力施加通過初始應變來實現。

圖8及式（13）中，E=1.96×l08 kPa;eP為預應力筋受拉屈服應變，參考美國加州抗震設計規范[14]，取0.0086;Nt為初始預加力;A為預應力筋截面積;εN為受壓屈服應變，取O0ε0為材料的初應變，當為負值時，預加力為初拉力。

算例中墩底豎向力為37599 kN，預應力筋截面積A取0.0032 lIl2，初始預加力N，取墩底豎向力12%，按式（13）計算得到的eo =-O.0072。

4 結果及其分析

4.1 墩身塑性鉸發展規律

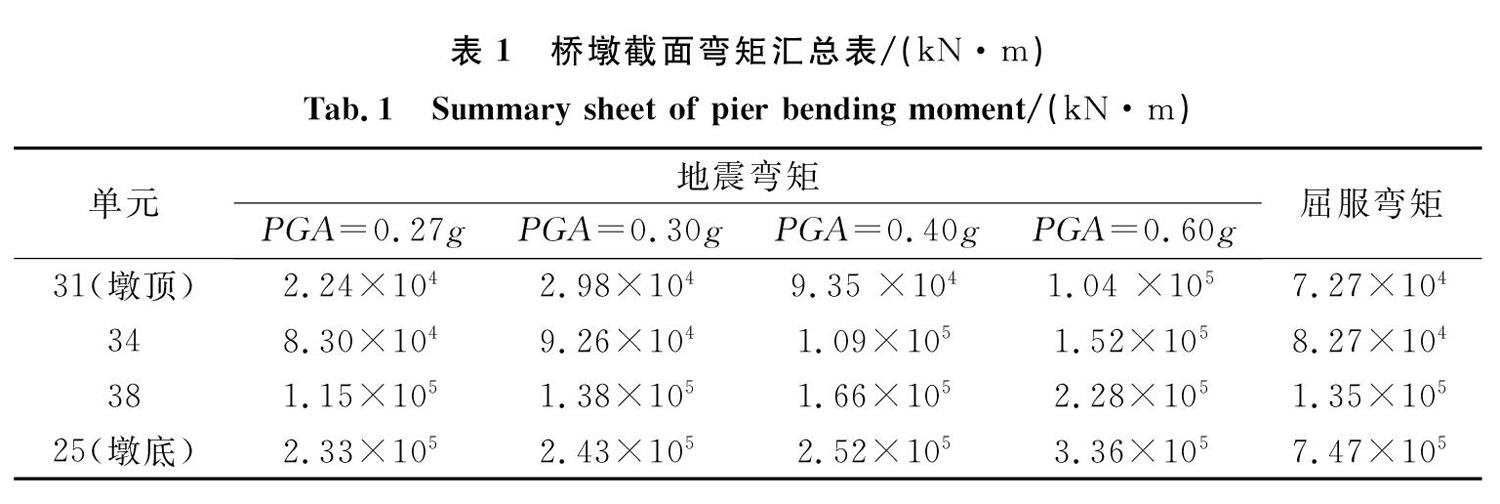
由參考文獻[8]可知，高階振型在墩身中影響較大的區域為距墩底40 m附近。本文對自復位橋墩順橋向進行增量動力分析，所得數據如表1所列，墩中塑性鉸位置及墩身彎矩和慣性力分布如圖9-11所示。圖表中，PGA為地震動峰值加速度，單元屈服彎矩選取J端截面、其數值采用XTRACT（截面彎矩曲率分析軟件）輔助計算。

從圖9及表1可知，當PGA =O. 27g時，34號單元（距墩底40 m）率先出現塑性;當PGA =0. 30g時，除34號單元出現塑性外，38號單元（距墩底29 m）也出現塑性，但墩底部位（2 5號單元）始終沒有出現塑性。

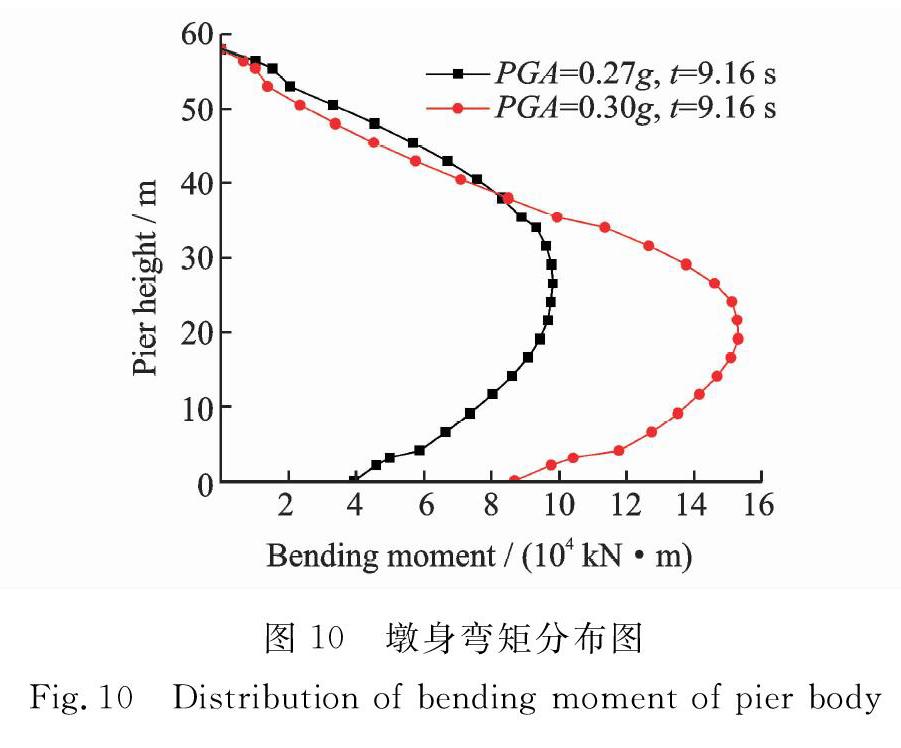
圖10和11分別為調整幅值為0. 27g和0.30g的Northridge強震記錄，在9.16 s（3 4號單元屈服時刻）墩身彎矩和慣性力分布圖。由圖1 0和1 1可知，彎矩及慣性力沿墩身高度呈高階模態的形式分布，這表明了高階振型的影響。

由表1結合圖10和11可知，在近場地震作用下，受高階振型的影響首先在距墩底40 m處出現塑性鉸;隨著地震動強度增大，在距墩底29 m處出現第二個塑性鉸區;自復位橋墩墩底沒有出現塑性鉸。這表明，自復位橋墩提離隔震并未減小高階振型效應。

4.2 各階模態響應

為了進一步考查各階模態效應對橋墩的作用，采用前述模態分解法近似求出了Northridge波作用下，橋墩關鍵截面最大彎矩出現時刻前3階模態彎矩值，如表2所示。3 4號單元屈服時（PGA—0. 27g），前3階模態彎矩與總彎矩時程曲線對比如圖1 2所示。

由表2及圖1 2和1 3可得：

（1）墩中產生塑性鉸區時刻墩底發生提離。本文參考文獻[15]計算得墩底提離彎矩為220175 kN.m，墩底第1階模態彎矩值大于墩底提離彎矩，這說明墩底提離主要由第1階模態貢獻。

（2）墩身塑性鉸區屈服時刻第2階模態彎矩貢獻率大，達到了70%左右，第1階模態彎矩貢獻率只占到20%左右。

（3）墩底第1階模態彎矩對總彎矩的貢獻率大，達到了93%，第2階比第3階模態彎矩貢獻率小。

4.3 各階模態響應貢獻率

本文選取QMi作為評價指標，按照前述方法考察了結構前3階模態對地震響應的貢獻，QM1反應了結構出現最大地震響應時刻各階模態的貢獻率。

表3列出了順橋向Northridge地震波作用下墩身關鍵截面彎矩前3階模態貢獻率;圖14繪出了墩中兩個塑性鉸單元前3階模態貢獻率柱狀圖。

由表3和圖14可得出：

（1）小震作用下，自復位高墩地震響應以第1階模態貢獻占主導地位。

（2）隨著地震動增大，第2階模態對墩身潛在塑性鉸區墩身彎矩的貢獻顯著，第2階模態貢獻最大為第1階模態的5倍。在進行自復位橋墩墩身抗彎設計時，必須考慮高階模態效應的作用。

（3）墩底主要由第1階模態彎矩貢獻控制，占到了總彎矩的93%，且不隨地震動的增大而發生顯著變化。因此對墩底進行抗彎設計時可不考慮高階模態的影響。

表4列出了順橋向Northridge地震波作用下前3階模態對墩頂位移貢獻程度。

由表4可得出：墩頂位移主要以前兩階模態貢獻為主，第1階模態的貢獻率能達到84%以上。隨著地震動的增大，第1階模態對墩頂位移的貢獻有增大的趨勢，這是由于墩底提離墩身出現搖擺剛體轉動位移，而這部分位移量是第1階模態作用產生的，第2，3階模態位移相比剛體位移很小。

5 結 論

（1）自復位高墩墩底不會出現塑性鉸，受高階模態的影響，墩中會形成塑性鉸，并且潛在塑性鉸區的位置與傳統高墩的相同。

（2）近場地震動下，自復位高墩第2階模態對墩中潛在塑性鉸區截面彎矩的貢獻顯著，最大時為第1階模態的5倍，前3階模態貢獻率大于78%。

（3）近場地震動下，自復位高墩的墩頂位移主要由第1階振型貢獻，其貢獻率大于84%，

參考文獻：

[1] 夏修身，陳興沖，鐵路高墩橋梁基底搖擺隔震與墩頂減震對比研究[J].鐵道學報，201 1，33 （9）：102-107.XIA Xiu-shen， CHEN Xing-chong. Controlled rockingand pier top seismlc isolation of railway bridge withtall piers[J]. Journal of the China Railway Society，2011， 33（9）：102-107.

[2] 夏修身，陳興沖，樁基礎高墩搖擺隔震分析模型研究[J].鐵道學報，2013 ，35（11）：86-91.

XIA Xiu-shen， CHEN Xing-chong. Study on analyti-cal model of rocking isolation for tall pier with pilefoundations[J]. Journal of the China Railway Society，2013，35 （11）：86-91.

[3] 夏修身，陳興沖，限位裝置對樁基礎高墩搖擺反應的影響[J].同濟大學學報（自然科學版），2013，41 （10）：1470-1475.

XIA Xiu-shen， CHEN Xing-chong. Effect of limitingdevice on the swing reaction of pile foundation tallpiers[J]. Journal of Tongji University （Science andTechnology），2013，41（10）：1470-1475.

[4] 夏修身，陳興沖，趙 揚，預應力效應對自復位高墩地震反應的影響[J].鐵道學報，2017 ，39 （12）：124-130.

XIA Xiu-shen， CHEN Xing-chong， ZHAO Yang. In-fluence of prestress effect on seismic response of selfrreset tall piers[J]. Journal of The China Railway So-ciety， 2017 ，39 （12）：124-130.

[5] 夏修身，李建中，近場地震動對樁基礎高墩搖擺反應的影響[J].哈爾濱工業大學學報，2014，46（4）：82-86.

XIA Xiu-shen， LI Jian-zhong. Effect of near groundmotion on the swing reaction of pile foundation tallpiers[J]. Journal of Harbin Institute of Technology，2014，46（4）：82-86.

[6] 李建中，宋曉東，范立礎，橋梁高墩位移延性能力的探討[J].地震工程與工程振動，2005，（1）：43-48.LI Jian-zhong， SONG Xiao-dong， FAN Li-chu. Dis-cussion on the displacement ductility of tall pier ofbridge[J]. Earthquake Engineering and EngineeringVibration， 2005， （1）：43-48.

[7] 盧 皓，管仲國，李建中，高階振型對高墩橋梁抗震性能的影響及其識別[J].振動與沖擊，2012，31（ 17）：81-85+98.

LU Hao， GUAN Zhong-guo， LI Jian-zhong. Theeffect of higher modes on the seismic performance oftall pier bridge and its identification[J]. Journal of Vi-bration and Shock，2012 ，31（17）：81-85+98.

[8] 夏修身，陳興沖，王常峰，鐵路高墩彈塑性地震反應分析[J].世界地震工程，2008，（2）：117-121.

XIA Xiu-shen， CHEN Xing-chong， WANG Chang-feng. Elastoplastic seismic response analysis of tallpiers in railway[J]. Earthquake Engineering and Engi-neering Vibration，2008， （2）：117-121.

[9] 祁 皚，徐 翔，高層隔震結構多階振型減震機理與傾覆問題研究[J].振動工程學報，2013，26（4）：487-492.

QI Ai， XU Xiang. Research on multi-modal dampingeffect and overturning problem of high-rise isolatedbuildings[J]. Journal of Vibration Engineering， 2013，26（4）：487-492.

[10] Hasan M R， Roke D， Huang Q. Quantification ofhigher mode responses for steel self-centering concetri-cally braced frames[C]. Honolulu， HI， USA： TheSeventh International Structural Engineering and Con-struction Conference， 2013：1-6.

[11]張育智，搖擺自復位高墩高階效應研究[J].振動與沖擊，2018，37（24）：66-71.

ZHANG Yu-zhi.A study on the higher mode effect ofrocking self-centering tall piers[J]. Journal of Vibra-tion and Shock， 2018，37（24）：66-71.

[12]盧 皓，李建中，橋梁高墩地震反應中高階振型貢獻程度的分析[J].石家莊鐵道大學學報（自然科學版），2012，25（04）：7-12.

LU Hao， LI Jian-zhong. Analysis of the contributionof higher modes in the seismic response of the bridgewith tall pier[J]. Journal of Shijiazhuang Railway Uni-versity （ Science and Technology） ， 2012 ，25 （04） ：7-12.

[13] Chopra A K. Dynamics of Structures： Theory and Ap-plications to Earthquake Engineering[M]. 4th ed. Up-per Saddle River， NJ： Prentice Ha11，2012：514-516.

[14] California Department of Transportation. CaltransSeismic Design Criteria：Version l. 6[S]. 2010.

[15]夏修身，陳興沖，李建中.高墩自復位隔震機理[J].中南大學學報 （自然科學版 ） ，2015 ，46 （7） ：2549-2557.

XIA Xiu-shen， CHEN Xing-chong， LI Jian-zhong. I-solation mechanism of self-centering tall pier[J]. Jour-nal of Central South University （Science and Technolo-gy） ， 2015，46（7） ：2549-2557.