試論變量的相對性及其作用

在方程、函數、不等式等數學式中出現的數量通常有常量、變量、參變量。一個數量是常量還是變量，是主變量還是參變量，其地位和性質是相對的，不是絕對的，是變化的不是靜止的。

我們解決數學問題，往往需要用不同的視角，不同的思維方式，不同的數學方法對問題進行轉化，將不熟悉的轉化為熟悉的，繁瑣的轉化為簡單的，抽象的轉化為直觀的，讓看似無法解決的問題迎刃而解，從“山窮水復疑無路”到“柳暗花明又一村”。在這個轉化過程中，不僅要將數學問題，在方程、不等式、函數等問題之間進行轉化，同時還要對一些數量的“身份”在常量、變量、參變量之間不斷地進行轉化。此時把一個字母當作常量，彼時又把這個字母當作變量；此地把一個字母看作主變量，彼地又把同一個字母看作參變量。正是數學問題的轉化和相應的變量在相對的變化的過程中問題就順利得以解決。

下面，筆者舉例說明變量的相對轉化在數學問題轉化中的必然性和作用。

例1.（1）求過圓x2+y2=R2（R＞0）上一點P（a，b）的切線方程.

（2）從圓外一點P（x0，y0）引圓x2+y2=R2（R＞0）的兩切線，切點為A、B，求切點弦AB的方程.

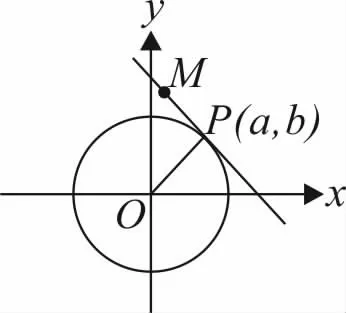
圖1

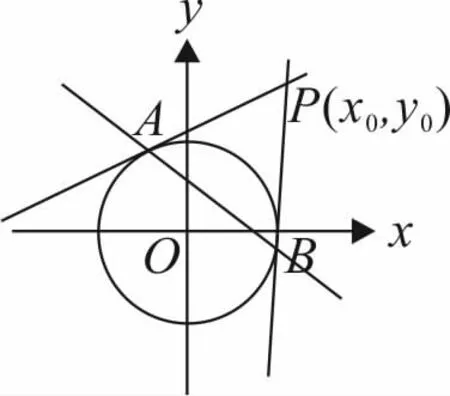
圖2

解析：（1）如圖 1 P（a，b）為切點，設 M（x，y）為切線上任一點.

這里a，b看作常量，x，y是變量，這即是過P點的切線方程.

（2）如圖 2，設切點 A（x1，y1），B（x2，y2）把 x1，y1，x2，y2看作常量

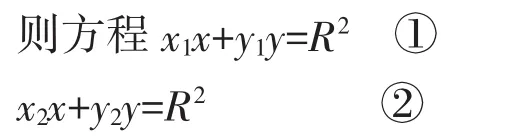
分別為過A，B兩點的切線方程.

∵ 兩切線方程都過 P（x0，y0）點.

在等式③、④中，把 x0，y0看作常量，把 x1，x2和y1，y2看作分別處在變量x，y的位置上，那么③④兩式可以看作：直線 x0x+y0y=R2過 A（x1，y1），B（x2，y2）兩點.

∴切點弦AB的方程為x0x+y0y=R2.

例 2.若關于 x的方程 ax+2b=0（a＞0）在區(qū)間（0，3）內有一個根.

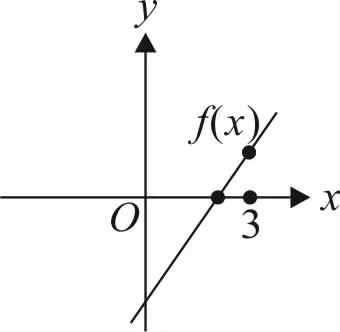
圖3

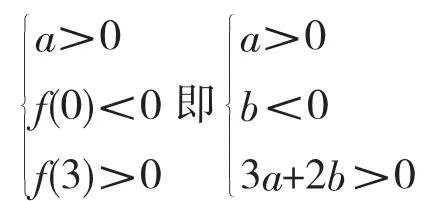
在前面的方程和函數中，把a，b看作是常量.

在不等式組和①式中把a，b看作變量。

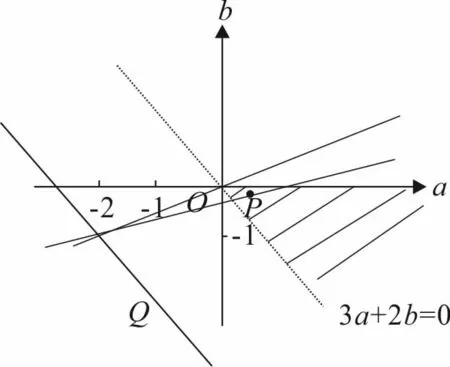
圖4

設點 A（-2，-1），P（a，b）為可行域內任一點.

問題轉化為求直線AP的斜率的最大、最小值.

由圖4可見，當點P在可行域內運動時，過A點的直線中，直線AO的斜率KAO最大，與直線3a+2b=0平行的直線AQ的斜率KAQ最小.

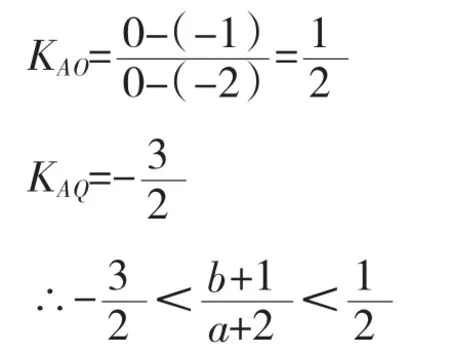
例 3.若不等式 2x-1＞m（x2-1）對于 -2≤m≤2恒成立.求x的取值范圍.

解析：如果將x看作主變量，m看作參變量，那么需要對m進行繁鎖的分類討論，我們換一種思維方式，把m看作主變量，x看作參變量，要2x-1＞m（x2-1）對于 -2≤m≤2恒成立.

即是關于m 的一元不等式（x2-1）m-（2x-1）＜0，當m∈[-2，2]時恒成立，再作一次轉化，將不等式問題轉化為函數問題.

就是關于 m 的一次函數 f(m)=（x2-1）m-（2x-1）當 m∈[-2，2]時 f(m)＜0 恒成立.

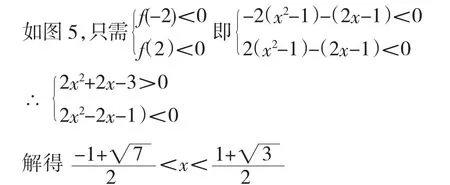
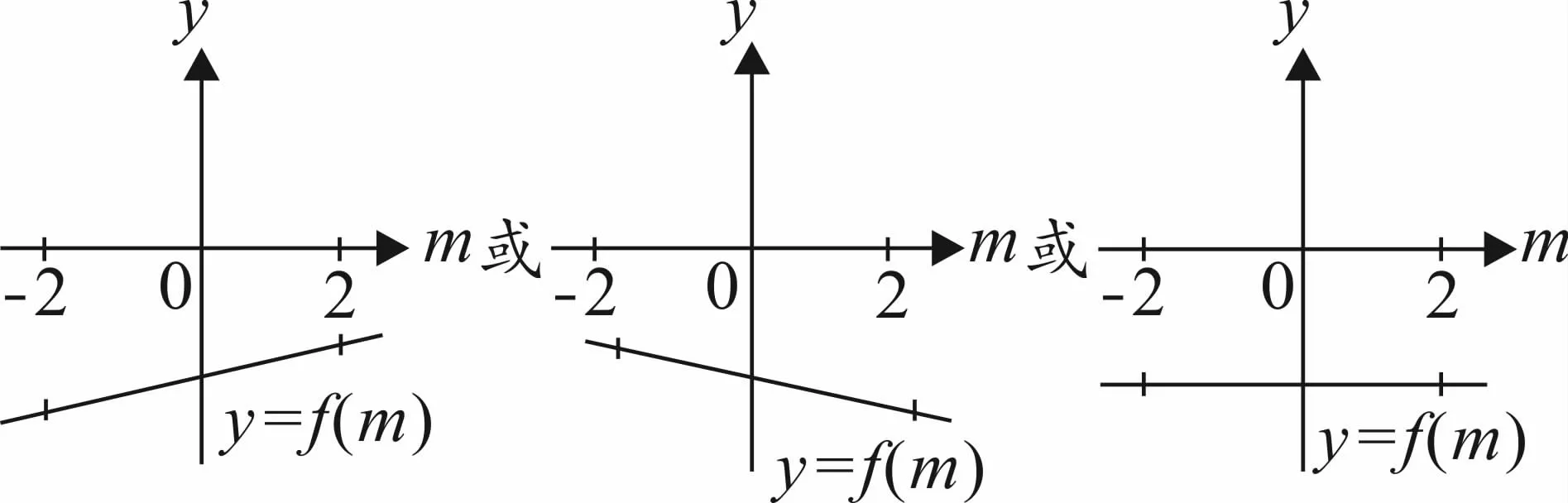
圖5

本題先對主變量和參變量的身份進行相互轉換，避免了對一元二次不等式的參變量進行繁雜的討論，然后將一元不等式的問題轉化為一次函數在一個閉區(qū)間的函數值問題，問題很快得到了解決。

例 4.設函數 f(x)=x3-3x2，若過點（2，n）可作三條直線與曲線y=f(x)相切，求實數n的取值范圍.

解析：f(x)=x3-3x2f′(x)=3x2-6x.

設（x0，y0）是一個切點，則過此點的切線斜率是

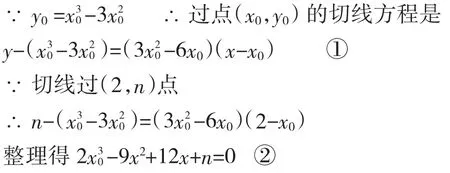
若將x0看作常量，則①式表示曲線y=f(x)的一條切線

因為過（2，n）點可以作曲線y=f(x)的三條切線

所以變量x0應有三個不同的值滿足等式②

即方程2x3-9x2+12x+n=0有三個不同的解

改寫成2x3-9x2+12x=-n

我們再把問題轉化為

函數g(x)=2x3-9x2+12x與函數y=-n的圖象有三個交點.為此，我們要求函數y=g(x)的極值點.

g′(x)=6x2-18x+12

=6（x-1）（x-2）

令 g′(x)=0 得 x1=1，x2=2

∵ 在(-∞，1]，[2，+∞)區(qū)間內 g′(x)＞0

∴g(x)為增函數

在（1，2）區(qū)間內 g′(x)＜0，g(x)為減函數.

∴g(x)在x=1處取極大值g(1)=5

在x=2處取極小值g(2)=4

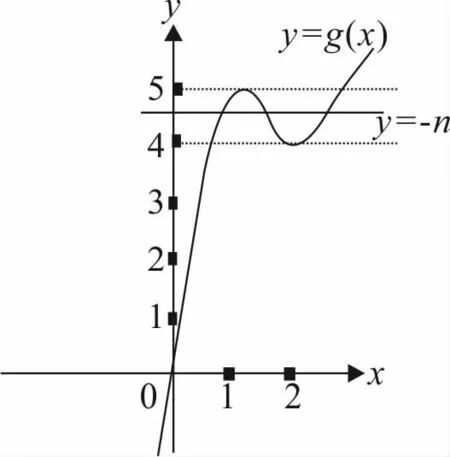
圖6

如圖6.若要y=g(x)與y=-n的圖有三個不同的交點

則要4＜-n＜5

即-5＜n＜-4

這就是實數n的取值范圍.

本題將切線問題轉化為方程的解的問題，然后又將方程的解的問題轉化為兩函數曲線的交點問題，在這個轉化過程中切點的橫坐標x0在常量和變量之間轉換，n也在常量和變量之間轉化。

其實一個量是常量、變量還是參變量是相對的，也是統(tǒng)一的。變量在變化的過程中取不同的值，常量可以看成是變量在變化的過程中取同一個值。不過在觀察、認識、解決問題的過程中為了敘述和處理的方便，我們需要將一些量看成常量、變量或參變量。對數學問題進行轉化是為了解決問題，讓一些量的身份進行轉化，是為了服務于問題的轉化，有利于問題的解決。所以，如果我們善于對數學問題進行轉化，善于在轉化的過程中讓一些量（或一些字母）扮演不同的角色，那么我們分析問題解決問題的能力就會顯著提高。