基于MATLAB的全地形車輛被動懸架動力學分析

孫 峰 張思崇戴 磊郭凌崧

（1-江蘇林海動力機械集團有限公司 江蘇 泰州 225300 2-天津大學內燃機研究所）

引言

懸架系統的作用是將車軸與車身連接起來以減輕由于路面不平而傳給車身的沖擊和振動，以及傳遞作用在車輪和車身之間的力和力矩。顯然，懸架系統對于提高車輛操縱穩定性，確保車輛安全功能起著重要作用[1-2]。

在車輛懸架設計中，懸架應滿足以下基本要求：行駛舒適性、減少動態道路輪胎力、減少車體之間的相對運動。懸架系統分為被動、半主動、主動懸架[3-4]。對于車輛動力學，車輛模型分為3類：整車模型，1/2車模型及1/4車輛模型[5]。1/4車輛模型是最簡單的2自由度一維模型，它假設車輛前軸和后軸的運動獨立振動，廣泛應用于車輛懸架的研究和設計[6-8]。本文研究的全地形車輛（Utility Vehicle），前后懸架均為雙橫臂式獨立懸架，結構形式屬于被動懸架，下文以前懸架為代表進行動力學研究。

1 懸架系統數學模型的建立

通過三坐標掃描獲得全地形車輛懸架系統重要零部件關鍵點的坐標值，利用逆向工程方法建立該全地形車輛雙橫臂式獨立前懸架系統的三維模型，如圖1所示。

圖1 某全地形車輛前懸架系統動態仿真模型

前懸架系統為左右對稱結構，因此在建立懸架系統數學模型時，下文以1/4車輛模型（前右懸架）為研究對象。盡管如此，前右懸架仍為一個復雜的多體系統，包括車輪及其附件、輪胎、減震器、懸架元件和1/4底盤及其剛性連接部件[5]。

在建立懸架系統數學模型前，需要對懸架系統進行合理的簡化抽象概述。圖2為1/4車輛簡化模型，其中，m1為簧下質量，m2為簧載質量，k1為輪胎的垂直剛度，k2為懸架的剛度系數，c1為輪胎的阻尼系數，c2為懸架的阻尼系數，x1為簧下質量的垂直位移，x2為簧載質量的垂直位移，y為路面激勵。

圖2 1/4車輛模型簡圖

對該1/4車輛模型進行受力分析，可以得到該懸架系統運動微分方程：

對上式進行變換得到：

表1給出了某全地形車輛的1/4車輛模型的參數。

表1 某全地形車輛的1/4車輛數學模型參數

參數y表示路面激勵，它是不規律的，可以選取多種不同類型，路面常見的駝峰有：弧形駝峰、梯形駝峰和多項式駝峰[9]。車輛以不同車速經過駝峰時的振動響應也會不同。本文選取階躍函數作為路面激勵，幅值為0.1 m，作為輸入函數來分析該懸架系統的動態特性，如圖3所示。

圖3 階躍激勵函數

2 懸架系統數學模型求解

對于方程（3）和（4）所表述的1/4車輛模型二階微分方程組，直接求解比較困難。MATLAB具有強大的數值方法來求解微分方程，本文使用MATLAB軟件對其進行求解[10-13]。

2.1 使用ODE45編程求解

ODE是MATLAB專門用于求解微分方程的功能函數。其中，ODE45求解器是一種自適應步長（變步長）的常微分方程數值解法，它采用了Runge-Kutta算法，是目前解決數值解問題的首選方法，而它只對一階方程有效[11]。

方程（3）和（4）是二階微分方程，為了求解該方程組，我們必須把它簡化成兩個一階微分方程。這里

通過引入新的變量來表示x˙2和x˙1，從而將方程（3）和（4）轉換為適合MATLAB求解的標準形式。令：

則有：

通過引入中間變量達到了降階的目的。此時有4個未知量v2，v1，x2，x1，可將方程（5）～（8）寫成：

式（9）為一階常微分方程組，即為MATLAB求解的標準形式。

這里通過MATLAB函數編程求解上述運動微分方程組。首先編寫一個單獨的函數文件來定義方程（9）；然后應用ODE45求解器調用該函數，對運動方程進行求解；最后繪制所需結果曲線圖。運行程序，可以得到車輛在階躍激勵作用下的簧載質量位移、簧下質量位移和兩者位移之差，如圖4所示。其中，x2表示簧載質量位移，x1表示簧下質量位移，x2-x1表示車身相對輪胎位移。

圖4 利用ODE45函數求解懸架系統運動微分方程

雖然利用ODE45函數編程可以求解微分方程，但是由于MATLAB函數運行方式比較抽象，因此理解和應用起來也較困難。除了可以直接通過函數編程（ODE45）來求解微分方程，MATLAB還提供了一些基于ODE45求解器開發的專用模塊，包括狀態空間模型（State-Space block）、傳遞函數（Transfer-Function block）和Matlab/Simulink[10]。這3種求解方法相比ODE45函數編程，數學模型和參數都易于理解，應用起來比較容易。

2.2 使用狀態空間模型求解

系統的微分方程描述是可以轉化為狀態空間模型的。因此，對于懸架系統運動微分方程組的求解，可以將系統運動微分方程轉化為狀態空間模型，通過求解狀態空間模型來達到求解微分方程的目的。狀態空間模型的一般形式為：

其中：X（t）表示狀態變量，U（t）表示輸入（或控制）變量，Y（t）表示輸出變量，A（t）表示狀態（或系統）矩陣，B（t）表示輸入矩陣，C（t）表示輸出矩陣，D（t）表示直接轉換矩陣。

將方程（3）和（4）寫成矩陣形式：

設定懸架系統的狀態變量為：

則有：

方程（14）和（15）即為該懸架系統運動方程的狀態空間模型。對于方程（14）和（15），在Matlab/Simulink中使用State-Space Block進行求解，如圖5所示。圖5a為懸架系統的狀態空間模型，圖5b為懸架系統的狀態空間模型參數。

圖5 懸架系統的狀態空間模型

將表1中所列的該車輛懸架模型參數以及圖3所示階躍函數輸入到圖5對應參數中。運行該程序，得到懸架系統的輸出變量：簧載質量位移x2、簧下質量位移x1、車身相對輪胎位移x2-x1，如圖6所示。

圖6 車輛懸架系統模型的輸出變量

2.3 使用傳遞函數求解

對于系統微分方程的求解，除了可以將其轉化為狀態空間模型進行求解，還可以使用傳遞函數來表述。對方程（1）和（2）進行拉氏變換，車輛懸架系統運動微分方程可寫為：

由方程（16）可得：

將方程（16）和（17）相加得到：

將方程（18）帶入方程（19）得到：

對上式化簡即可得到輪胎位移x1相對路面激勵y的傳遞函數：

其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，B3=m2c1，B2=m2k1+c1c2，B1=A1=c2k1+c1k2。

對于方程（21），可在Matlab/Simulink中使用Transfer Function Block進行表述，如圖7所示。

圖7 簧下質量位移相對路面激勵的傳遞函數模型

將表1中所列懸架系統參數和圖3所示階躍函數輸入到圖7參數中。運行該程序，得到輪胎在階躍激勵下的垂直方向位移變化曲線，如圖8所示。

圖8 簧下質量位移階躍激勵響應曲線

類似地，可以得到簧載質量位移x2相對路面激勵y的傳遞函數：

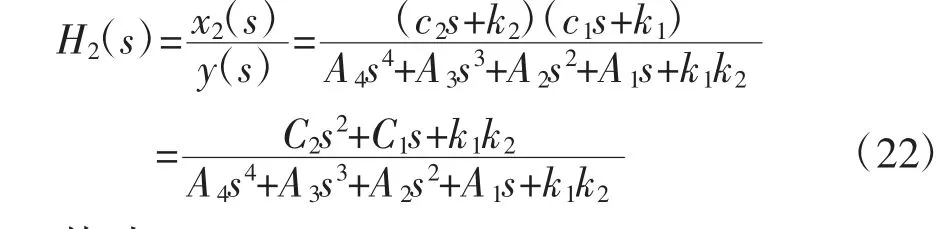
其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，C2=c1c2，C1=A1=c2k1+c1k2。

對于方程（22），在Matlab/Simulink中使用Transfer Function Block進行表述，具體步驟與圖7表述類似，這里不再贅述。運行程序，得到車身在階躍激勵下的垂直方向位移變化曲線，如圖9所示。

圖9 簧載質量位移階躍激勵響應曲線

同理，可以得到車身相對輪胎位移變化量對于路面激勵的傳遞函數：

其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，D3=-m2c1，D2=-m2k1，D1=0，D0=0。

對于方程（23），可在Matlab/Simulink中使用傳遞函數進行表述，相關步驟與上面類似，此處不再贅述。運行程序，得到在階躍激勵下車身相對輪胎垂直方向位移變化曲線，如圖10所示。

圖10 簧載質量相對簧下質量位移階躍激勵響應曲線

車身位移變化量僅僅表示振動幅值大小，而車輛乘坐舒適性通常以車輛通過駝峰時的最大簧載質量加速度來衡量。簧載質量加速度是簧載質量位移相對時間的二階導數。其中，位移、速度、加速度三者之間的關系為：

方程（1）和（2）按照加速度、速度、位移變量來表達，可以寫為：

對方程（24）～（26）進行拉氏變換，得到：

與方程（18）～（21）類似處理，可以得到簧載質量加速度a2相對路面激勵y的傳遞函數：

其 中：A4=m1m2，A3=m2c2+m2c1+m1c2，A2=m2k2+m2k1+m1k2+c1c2，A1=c2k1+c1k2，E4=C2=c1c2，E3=C1=c2k1+c1k2，E2=k1k2，E1=0，E0=0。

對于方程（29），在Matlab/Simulink中使用傳遞函數進行表達求解，具體步驟與圖7表述類似。運行程序，得到在階躍激勵下的車身垂直方向加速度變化曲線，如圖11所示。

圖11 簧載質量加速度階躍激勵響應曲線

2.4 使用Matlab/Simulink模塊求解

使用狀態空間模型和傳遞函數方法求解微分方程，都需要將系統運動微分方程轉化為相應的模式再進行求解。而Matlab/Simulink模塊，可以對系統運動微分方程組（方程（3）和（4））直接輸入表達進行求解，如圖12所示。

圖12 利用Matlab/Simulink求解懸架系統運動微分方程

將表1中所列參數數值和圖3所示路面激勵函數輸入到圖12中的Matlab/Simulink模塊對應參數。運行該程序，可以得到懸架系統運動方程的狀態變量在路面激勵狀況下的響應曲線，如圖13所示。

可以看出，簧下質量位移波動較小，簧載質量位移波動振幅較大（振動最大幅值約為激勵幅值的1.7倍），說明輪胎受路面激勵變形很小，而車身受路面激勵影響產生較大振動；圖13c和圖13d能較近似反映車輛乘客的乘坐舒適性，在激勵產生后的前2 s，乘客會受到較大振動幅值的影響。

圖13 1/4車輛模型在路面階躍激勵下的響應

由以上分析可以發現，使用狀態空間模型、傳遞函數和Matlab/Simulink模塊3種方法求解得到1/4車輛模型運動微分方程輸出變量，與使用ODE45函數求解得到的結果是一致的。但從操作難易、實際應用等方面考慮，求解微分方程時可優先使用Matlab/Simulink模塊，再者是狀態空間模型和傳遞函數，最后是ODE45求解器。

根據ISO 2631[13]要求，乘坐的舒適度范圍是車身垂直加速度不超過0.8 m/s2。由圖11和圖13d可以發現，階躍激勵作用的前2 s，車身加速度幾乎都超過該限值。因此，該車輛的乘坐舒適性還有進一步提升的空間。

3 懸架阻尼對車輛振動的影響

本文研究的某全地形車輛懸架系統為被動懸架，懸架阻尼為固定值750 Ns/m。為了分析懸架阻尼對車輛動力學的影響，設定懸架阻尼c2的取值分別為250 Ns/m、500 Ns/m、750 Ns/m、1 000 Ns/m及1 250 Ns/m，再次通過ODE45函數編程，得到在相同的路面階躍激勵作用下，車輛懸架阻尼取不同值時對應的5組懸架系統簧載質量位移變化曲線，如圖14所示。

圖14 懸架系統選取不同阻尼時的輸出變量

可以發現，懸架阻尼對車輛振動的影響還是比較大的。懸架阻尼較小時，雖然單位時間內振幅不大，但振動衰減比較緩慢，乘坐舒適性相對較差；懸架阻尼較大時，雖然振動衰減時間短，但單位時間內振幅較大，乘坐舒適性也不太好。本文研究的某全地形車輛懸架阻尼值介于中間，比較合理。

4 結論

1）通過逆向工程技術建立了某全地形車輛前懸架系統三維模型，并將其簡化為1/4車輛數學模型。

2）分別使用狀態空間模型方法和傳遞函數及Matlab/Simulink模塊3種方法對所建的數學模型運動微分方程進行了求解，與使用ODE45求解器得到結果具有一致性，并給出優先使用順序。

3）以簧載質量位移和加速度作為乘坐舒適性評價指標對某全地形車輛的振動特性進行了分析，為進一步研究車輛動態特性奠定了基礎。

4）分析了懸架阻尼對車輛振動的影響，驗證了某全地形車輛懸架阻尼設計的合理性，對提升車輛乘坐舒適性具有一定理論指導意義。