基于滅點優化的單幅圖像三維重建

，，

(浙江工業大學 理學院，浙江 杭州 310023)

三維重建是計算機視覺領域和計算機圖形學的一個重要的研究方向,其應用領域十分廣泛，大批學者[1-3]進行了三維重建在各個領域的應用研究。三維重建是指根據單幅圖像或者多幅的圖像重建三維信息的過程。基于單幅圖像的三維重建避免了基于多幅圖像重建的特征匹配的問題，現實中基于單幅圖像的三維重建取材方便，簡單的幾步交互操作加以塑造，重建場景，比耗時費力的傳統方法更優越。對于減少建模的成本和解放人力意義重大，所以有必要研究單幅圖像的三維重建技術。滅點對應著場景的三維方向，是二維圖像中的重要信息，通過滅點可以重建場景的幾何信息[4]，獲得相機的參數[5]，實現物體的三維重建。近年來，大批學者進行單幅圖像的三維重建的研究。Criminsi等[6]進行了的單像量測的相關研究，并于2000年正式提出所謂單像量測(SVM，Single view metrology)的概念,即通過單張影像上的幾何信息(尤其是滅點)進行測量。錢晶晶等[7]利用手動標定重要的點和平行線，利用滅點性質進行標定，但結果不夠精確。Nian等[8]提出了一種利用建筑物對稱性的相機標定方法。首先是利用建筑物結構的對稱性進行相機標定，根據標定結果恢復出1 組三維點。然后手動標記出建筑物的各個組件，通過恢復三維點確定組件的位置和形狀，但僅適用于對稱物體。Tardif[9]則采用J-linkage算法生成多于3 類候選滅點的最小采樣集，然后根據候選滅點與直線間的一致性度量函數有效去除外點。該算法可以解決復雜建筑物環境下的滅點檢測問題，實現建筑物的三維重建，但必須給定攝像機的內參數信息。Xu等[10]提出的一種帶有統計特性的一致性度量方法，綜合考慮了直線端點誤差、直線的長度及位置的影響，提高了滅點的檢測精度。王思潔等[11]基于結構化的單幅圖像建筑物，利用平行平面與包含垂直信息的任意平面的平面模型解算三維坐標，實現三維重建。

在上述研究的基礎上，改進原來滅點檢測算法未充分利用產生滅點的直線的參數信息的特點。先利用Canny算子提取出圖像邊緣，再利用Hough變換提取出圖像中的長直線，分析直線特征，對不同方向的直線進行分組，根據各方向的直線滿足線性分布關系，利用改進的回歸算法建立直線參數的線性模型，充分利用了直線信息，剔除外點，提高了檢測滅點的精度。并利用滅點的性質對攝像機的內外參數進行標定，然后交互獲得最少的二維點，通過計算求得的攝像機內外參數和物體本身的幾何特征計算相應的三維坐標，最后進行目標物體的三維重建。

1 滅點檢測算法

滅點是在空間一組平行線的無窮遠點經過透視投影在二維圖像中形成的像的直線在圖像上的投影線段的交點。獲取單幅圖像上的滅點一般采用自動法，因為自動法人機交互少，自動化程度高。步驟如圖1所示。

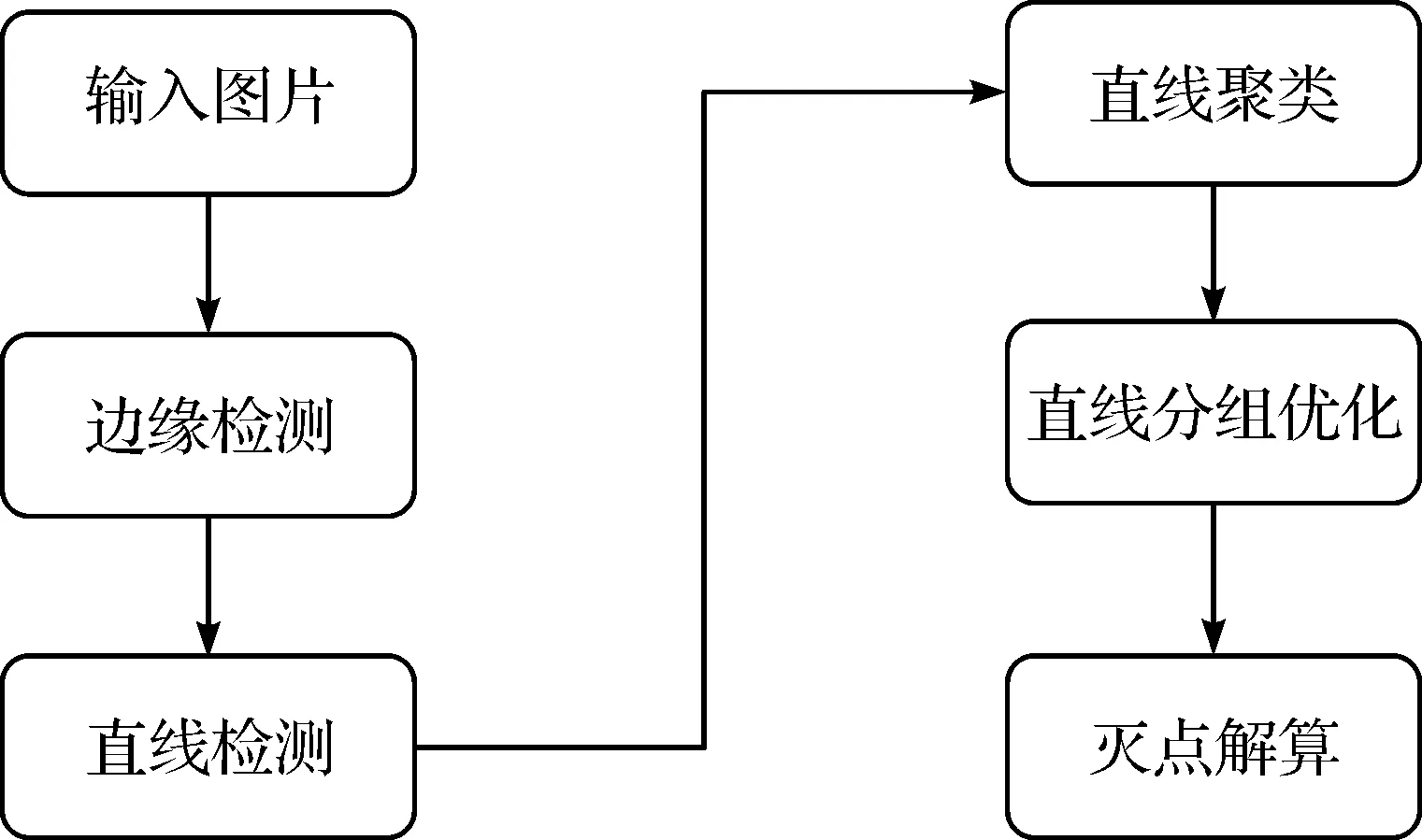
圖1 滅點檢測算法步驟Fig.1 The steps of vanishing point detection algorithm

1.1 圖像邊緣檢測

邊緣檢測有多種算子可以運用，運用各類算子進行邊緣檢測，實驗結果如圖2所示。

圖2 各類算子邊緣檢測Fig.2 Edge detection of all kinds of operators

通過圖2實驗對比得出可以提取較好和較多的圖片細節，提取的邊緣效果很好，所以選擇canny算子進行圖像邊緣檢測。

1.2 直線的獲取與分組

目前獲取直線較好的方法為Hough變換直線，通過Hough變換可以提取圖像中的直線信息并將其轉化到參數空間。坐標軸空間一條直線對應(ρ,θ)參數空間一個點(ρ0,θ0)。重構的三維物體是規則的長方體，故其在圖像空間中會形成水平方向，垂直方向與縱深方向的直線，對直線進行分組的方法很多，但是由于需要分組的直線在角度上明顯特征，所以根據直線的角度方向可以將圖像中的直線分為對應方向上3 類，此方法有效并且快速的實現了直線的初步分組，具體做法為

第1步設置第一條直線的傾斜角為判斷初始值θ0， 判斷余下的直線，若直線的θ∈θ0-15°，θ0+15°， 則將直線放入第1 組。

第2步重新歷遍存放直線的數組，若θ?θ0-15°，θ0+15°， 則把檢測到的第1個θ值作為新的θ1， 把滿足θ∈(θ0-15,θ0+15°)的直線放在第2 組。

第3步將第1組直線的傾斜角取平均值，得到新的θ0， 重新歷遍存放直線的數組，若θ∈θ0-15°，θ0+15°，則將直線放入第1 組。第2 組進行同樣的操作，剩余的直線放在第3 組。

1.3 分組直線優化

根據文獻[12]證明得到對應滅點的直線束在(ρ,θ)參數空間滿足線性分布關系，對于有誤差樣本點的數據集合，為了得到精確滅點，剔除掉無效直線，充分利用直線參數信息，采用改進的回歸算法作為參數線性模型的估計算法。

假設圖像某一方向有n條直線束，分別記為L(ρ(i),θ(i))(i=1,2, …,n)。那么，這n條直線束對應的參數(ρ(i),θ(i))應該滿足的一般線性表達式為

ρ(i)=βTθ(i)+ε(i)i=1,2, …,n

(1)

式中：(ρ(i),θ(i))為n條直線束中第i條直線的參數；β=(β0,β1)為直線參數的線性模型參數；ε(i)為隨機誤差。為了抑制誤差點的影響，估計出有效的參數，根據滅點直線的特征，將直線的重要性引入參數線性模型的估計算法中，對于滅點直線來說，它的重要性與其長度成正比，和該直線的傾斜角與其余傾斜角的角度差之和成反比，給每條直線分配一個W(i)(i=1,2, …,n)為

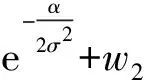
(2)

式中：α為指定直線的傾斜角與其余傾斜角的角度差之和；σ為魯棒性閾值，設定為0.1；l為直線的長度；w1，w2為權重，其中w1=0.7，w2=0.3。

采用改進回歸算法的線性擬合目標函數為

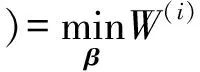
(3)

使目標函數達到最小值時的β0,β1值即為穩健回歸算法所求線性模型的參數值。這樣得到了直線參數模型，重新估計之前的樣本點，若遠離目標函數的此樣本點就是無效點，則通過設立有效的閾值，距離大于閥值的即為無效點，參數空間中對應的點為圖形空間中的相應直線，通過該算法就可以有效剔除了無效直線。

1.4 滅點求取

根據文獻[13]利用最小距離法求解滅點的坐標。設滅點直線束l1,l2,…,ln對應的滅點為vp，將li和vp都表示為齊次坐標的形式(a,b,c)T，則有

Mvp=0

(4)

式中M=[l1,l2,…,ln]T，li=[Ai,Bi,Ci]，對應的直線方程為Aix+Biy+Ci=0。

將利用最小距離法求解最佳滅點的問題轉化為線性代數的問題，根據拉格朗日不定乘子法，將滅點的求解過程轉化為數學問題，滅點為對稱矩陣MTM最小特征值的特征向量。

2 相機內外參數的標定

利用滅點的性質進行相機標定，假設相機的投影點是圖像的中心。攝像機的內外參數采用透視投影模型進行研究，根據文獻[14]的介紹得到圖像坐標系，攝像機坐標系，世界坐標系之間的轉換關系。Fu,Fv是由兩條互相垂直的平行線得到的滅點，Fu,Fv在攝像機坐標下的坐標分別為(xcu,ycu,f),(xcv,ycv,f),借助王建的攝像機標定方法[15]得到焦距f為

(5)

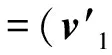
世界坐標系中，滅點為3 個方向上的無窮遠點，令這3 個方向為X軸，Y軸，Z軸方向，則有：v1=(1,0,0),v2=(0,1,0),v3=(0,0,1)，則有

(6)

相機的平移向量與相機坐標系相對世界坐標系的位置有關，因此，任意指定世界坐標系的原點，若其在圖像上的坐標為(u,v)，則平移矩陣T的表達式為

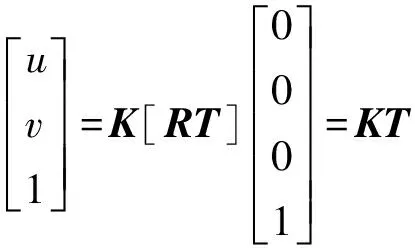
(7)

式中：λ=f；K為內參數矩陣，由焦距和投影中心坐標確定。

3 物體的三維重建

空間點的成像原理如圖3所示，O為相機中心，ABCD為長方體的一個面，abcd為透視投影到圖像平面的四邊形。

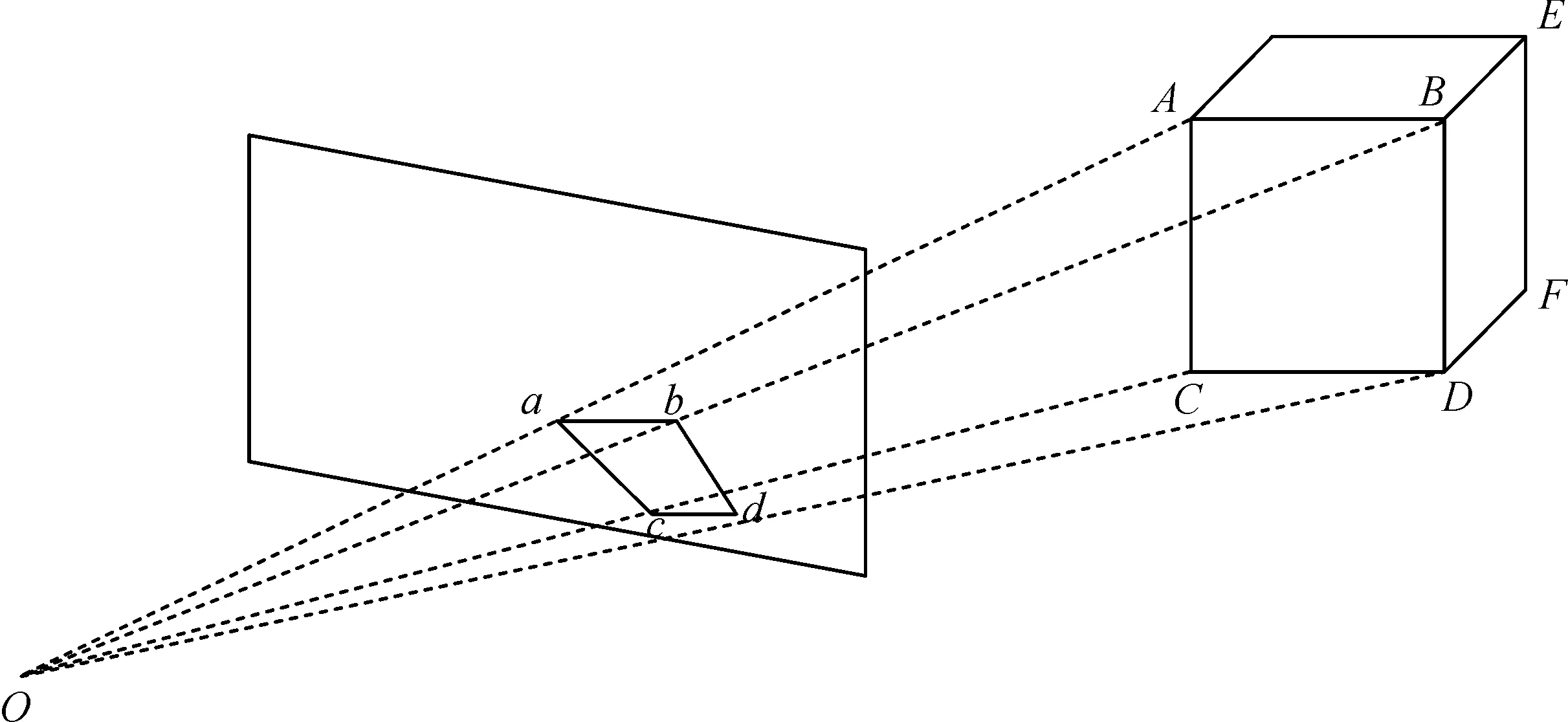
圖3 空間點的成像原理Fig.3 The imaging principle of space point

手動獲得abcd4個頂點的圖像坐標，通過固定其D點的深度坐標Z，通過AB=CD，即可確定ABCD與投影面的距離。根據圖像點與空間的轉換公式就可以算出其他三點的深度值，從而計算出AB和AC的相對長度。同理通過BF=DE，能求出BF的長度，確定重建長方體的長寬高。最終得到的三維模型與實際模型之間僅存在比例縮放關系，不影響其結構。

4 實驗結果

根據角度進行直線束的初步分組后，再根據改進后的穩健回歸算法得到參數線性模型，利用線性模型剔除外點得到的有效直線結果如圖4～6所示。

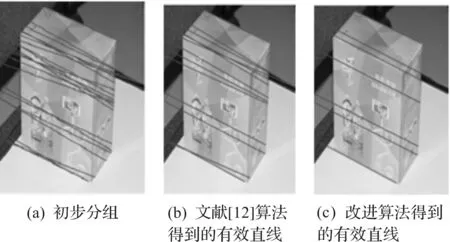
圖4 圖像的水平方向Fig.4 Horizontal direction of image

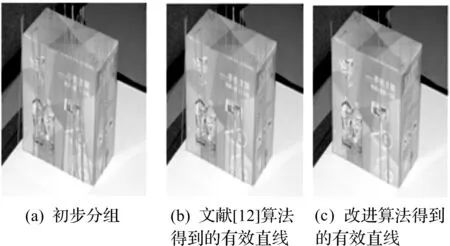
圖5 圖像的垂直方向Fig.5 The vertical direction of the image

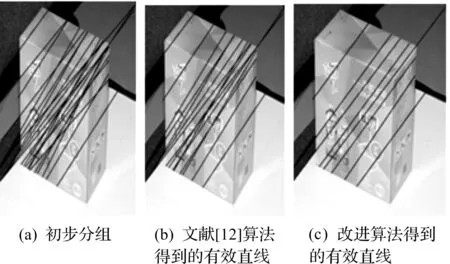
圖6 圖像的縱深方向Fig.6 The depth direction of the image

圖4～6中的(a)表示直線初步分組后得到的直線；圖4，5中的(b)表示利用文獻[12]介紹的算法得到的有效直線，圖6中的(b)表示利用文獻[12]介紹的算法得到的有效直線；圖4～6中的(c)是根據改進后的穩健回歸算法得到的有效直線。從圖4～6中可以發現：改進算法有效地剔除了無效直線，優化了結果。

為驗證改進算法的有效性和泛化能力，進行了實驗2，3，實驗結果如圖7～12所示。

圖7 實驗2圖像的水平方向Fig.7 Horizontal direction of the image

圖8 實驗2圖像的垂直方向Fig.8 The vertical direction of the image

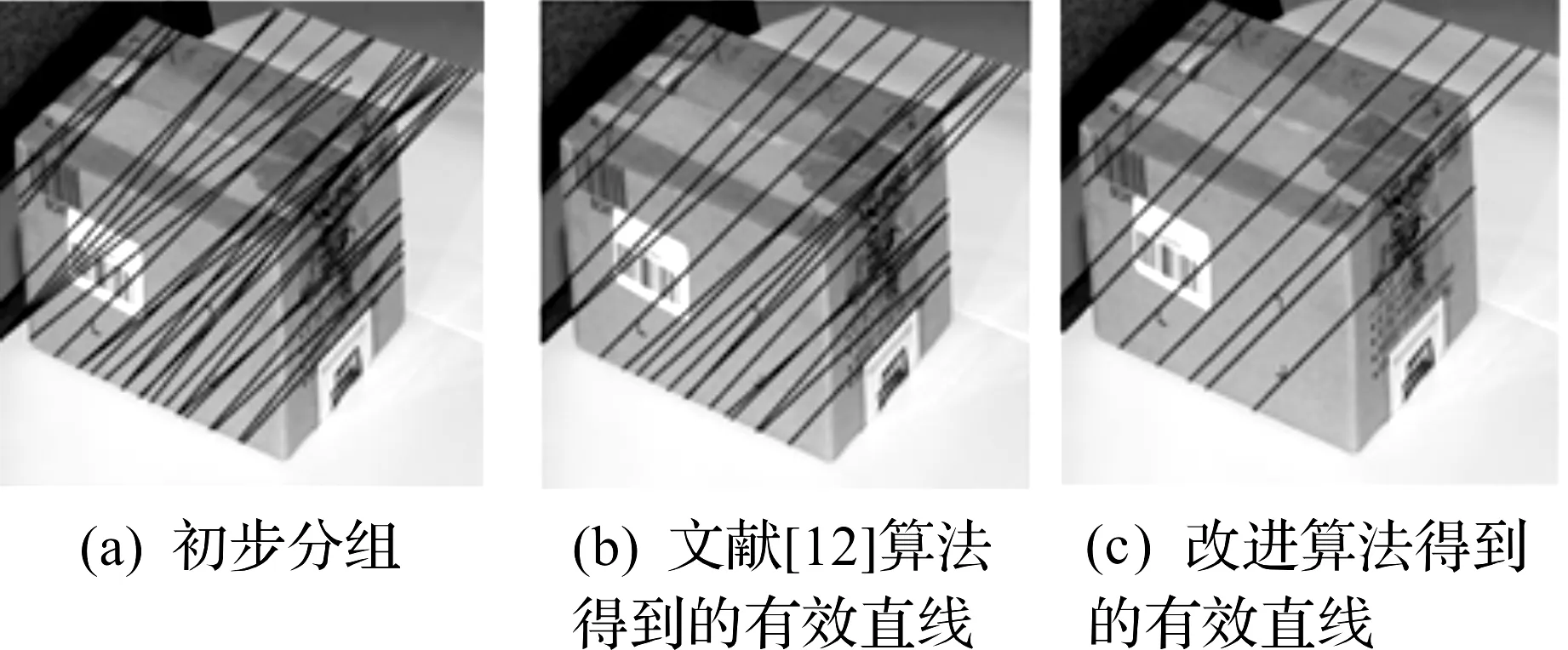
圖9 實驗2圖像的縱深方向Fig.9 The depth direction of the image

圖10 實驗3圖像的水平方向Fig.10 Horizontal direction of the image

圖11 實驗3圖像的垂直方向Fig.11 The vertical direction of the image

圖12 實驗3圖像的縱深方向Fig.12 The depth direction of the image

從實驗結果得出改進算法比文獻[12]的算法更有效，將直線的重要性引入參數線性模型的估計算法中，能最大化地利用直線的參數信息，剔除無效直線的影響，提高滅點計算精度。并且具有良好的泛化能力。

通過之前的介紹，假設圖3中D點對應的深度值為2f時，手動獲取圖像中的部分二維點，計算出長方體的邊長如表1所示。

表1物體長度測量值及誤差表

Table1Themeasurementvalueanderrortableofthelengthoftheobject

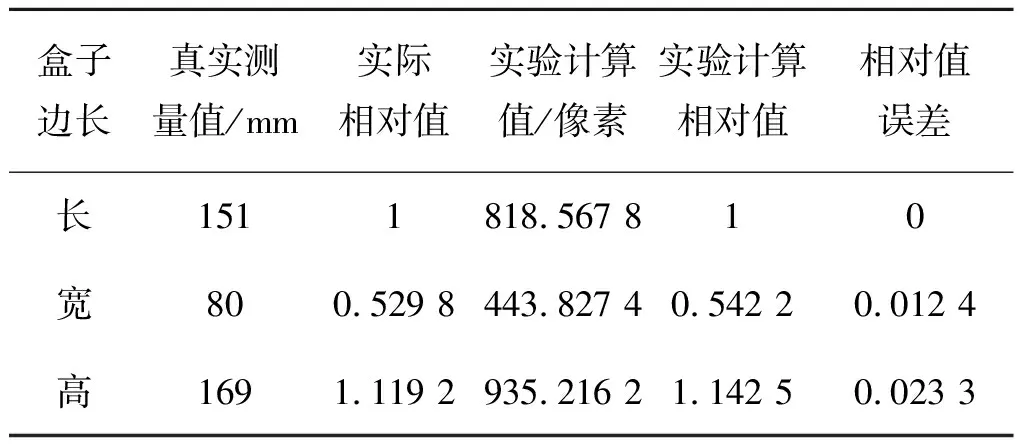
盒子邊長真實測量值/mm實際相對值實驗計算值/像素實驗計算相對值相對值誤差長1511818.567 810寬800.529 8443.827 40.542 20.012 4高1691.119 2935.216 21.142 50.023 3

實際相對值是令盒子長度的相對值為1，通過比值得到寬和高的相對值，相對值誤差是實際相對值與實驗計算相對值之差的絕對值。由于寬和高的相對值誤差都小于2.5%，故建模的整體誤差在2.5%以內，符合建模要求。

根據求得的物體的長寬高，用OpenGL實現三維重建，實驗結果如圖13所示。

圖13 原圖像與三維重構后的圖像Fig.13 Original image and 3D reconstructed image

5 結 論

介紹了利用規則物體的單幅圖像三維重建，針對目前的滅點檢測算法尚未充分利用產生滅點直線的參數信息，首先用canny算子和Hough變換檢測出直線，根據滅點直線特征對直線進行聚類，采用改進的回歸算法作為參數線性模型的估計算法剔除外點，從而得到了有效直線。此方法有效地剔除了圖像中無效直線的干擾，從而可以計算出精確的滅點，根據滅點的屬性得到相機的內外參數，根據長方體的幾何性質實現三維重建。此方法有效地提高了模型的精度，模型整體精度在2.5%以內，符合三維重建精度要求。可試用于規則建筑物的三維重建。該方法也有一些缺陷，僅實現規則物體的重建，接下來會研究不同形狀的幾何體的單幅圖像三維重建。因滅點檢查算法還有很多方面有待提高，接下來還可以再研究如何提高滅點精度。