吸血蝙蝠與牛群間狂犬病毒的傳播研究

張菊平，李 丹

(1.山西大學 復雜系統研究所， 太原 030006；2.疾病防控的數學技術與大數據分析山西省重點實驗室， 太原 030006)

狂犬病是由狂犬病毒引起的人和其他所有哺乳動物的急性致死性中樞神經系統的自然疫源性疾病，病死率高，呈全球性分布，是世界上最致命的傳染病之一[1-2]。該病只通過唾液、血液傳播，潛伏期內不傳播,也不母嬰傳播。吸血蝙蝠[3-5]是狂犬病病毒的自然宿主,其體型小，一次生產一胎，平均壽命為12年。吸血蝙蝠傳播狂犬病毒的方式為以下4種[5]：① 吸食動物血液；② 抓傷動物；③ 吸血蝙蝠呼出的大量氣溶膠傳播；④ 口腔感染(常見于蝙蝠種內傳播)。吸血蝙蝠主要通過吸食動物或人的血液來傳播狂犬病毒，是狂犬病在動物和人之間傳播的重要媒介之一。牛狂犬病的發病牛以犢牛和母牛較多見，該病常在一個地區內散發，潛伏期平均30～90 d，病程3～7 d。

近年來吸血蝙蝠傳播致命的狂犬病毒越來越引起人類重視。比如在1996年,WARNER等[6]從秘魯的兩例致命病例腦組織樣本中測試證實樣本中存在的狂犬病毒與吸血蝙蝠所攜帶的最為接近。ARELLANO-SOTA等[7]對秘魯的阿普里馬克省調查發現，2014年有505～724 頭牛被蝙蝠噬咬而感染狂犬病致死，造成巨大經濟損失。為有效控制吸血蝙蝠狂犬病毒的傳播，在阿根廷和墨西哥進行的試驗中證明接種疫苗可以有效保護牲畜免受狂犬病毒的侵害[8]。Streicker等[9]對秘魯的4個地區的20個吸血蝙蝠種群進行縱向捕獲-重新捕獲研究， 發現幼年和次成年吸血蝙蝠體內所含血清陽轉率最高，所以重點捕殺成年蝙蝠可以減緩狂犬病毒的傳播。

本文以吸血蝙蝠與牛間的相互關系為基礎，建立數學模型，求得系統的閾值并分析了平衡點的穩定性，針對系統中牛群免疫率參數進行了敏感性分析，最后給出控制狂犬病毒傳播的預防措施。

1 建立模型

根據吸血蝙蝠與牛群間狂犬病毒傳播機制做如下假設：① 忽略牛群間狂犬病毒的傳播；② 蝙蝠潛伏期和發病期的病毒累積量不同，假設血清陽轉率不同；③ 養牛場每年均會引入一批牛犢來保持數量的恒定，假設牛群有常數輸入，指數輸出。 狂犬病毒在吸血蝙蝠與牛群間的傳播流程如圖1所示。

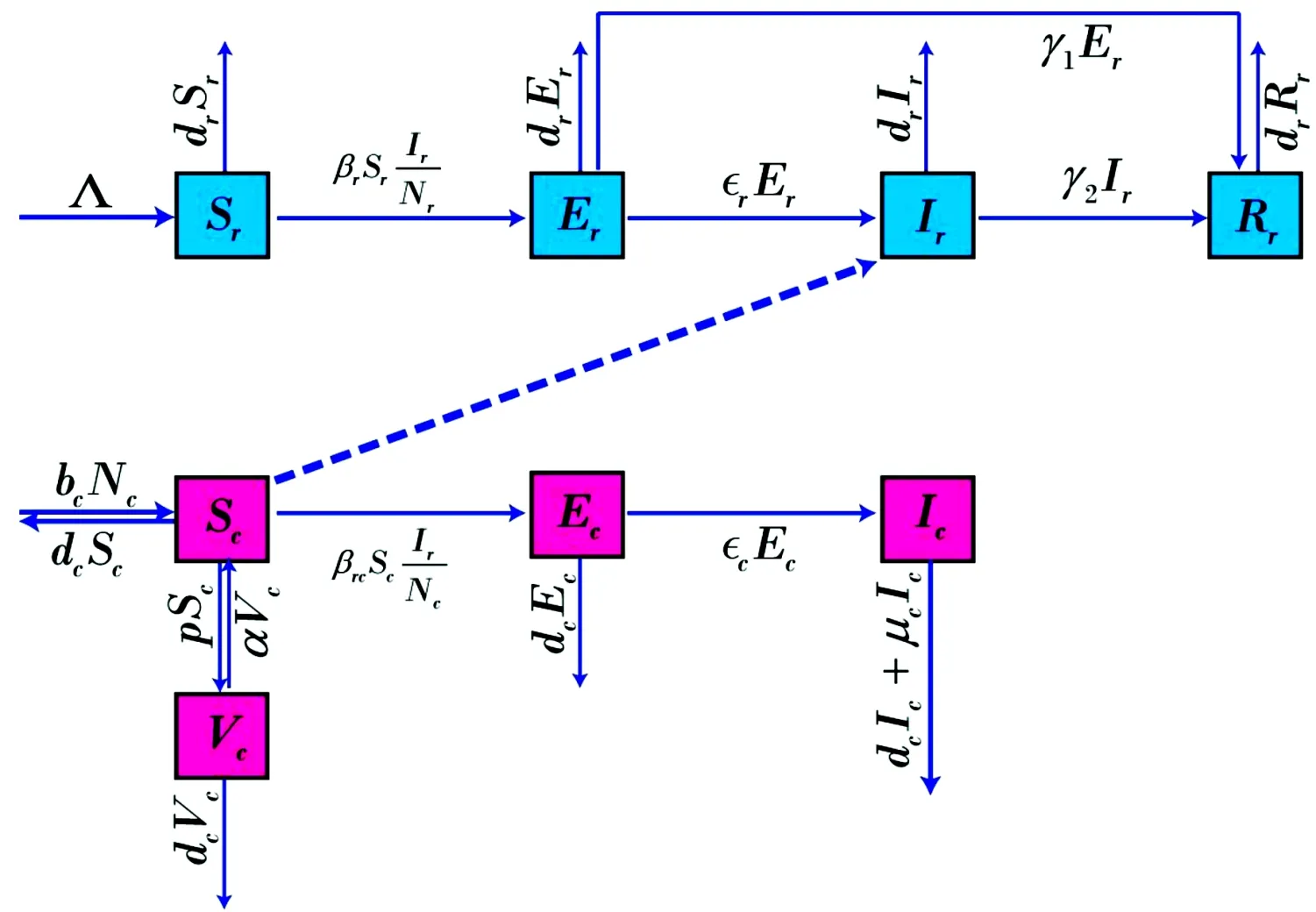
圖1 吸血蝙蝠與牛狂犬病毒傳播流程

流程圖中參數說明：記吸血蝙蝠群體總量為Nr=Sr+Er+Ir+Rr,其中Sr、Er、Ir、Rr分別表示易感者、潛伏期、染病者和恢復者吸血蝙蝠，吸血蝙蝠的出生率和死亡率分別為br和dr,且br=dr,發病蝙蝠感染易感蝙蝠的傳染率為βr,潛伏期到發病期的轉化率和血清陽轉率為εr和γ1，發病期的陽轉率為γ2。Sc、Ec、Ic、Vc分別表示易感者、潛伏期、染病者和接種者牛。記牛群總數為Nc=Sc+Ec+Ic+Vc；牛的輸入為Λ；死亡率和因病死亡率為dc和μc；牛從潛伏期到發病期的轉化率為εc；發病蝙蝠感染易感牛的傳染率為βc；接種免疫率和免疫失效率分別為p和α。

根據傳播流程建立相應的動力學模型如下：

(1)

2 模型分析

2.1 吸血蝙蝠模型穩定性分析

由于模型(1)的前4個方程和后4個方程獨立，且滿足Nr=Sr+Er+Ir+Rr，因此將前4個方程降維歸一化得：

(2)

系統(2)的正向不變集為

Γr={(sr,er,ir)∈R3∣0≤sr,

er,ir≤1,sr+er+ir≤1}

系統(2)的無病平衡點為P0(1,0,0)，根據下一代矩陣理論[10]得

故系統(2)的閾值為

定理1 當Rr0<1時，無病平衡點P0是全局漸近穩定的。

證明由于sr≤1，可得系統(2)的輔助系統為

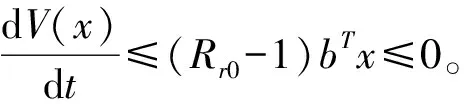
定理2 當Rr0>1時，系統(2)的無病平衡點不穩定，存在唯一的正平衡點P*且全局漸近穩定的。

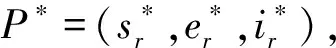
(3)

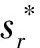
從而，當Rr0>1時，系統(2)存在唯一的正平衡點為：

系統(2)在P*點處的Jacobian矩陣為

其特征方程為λ3+a1λ2+a2λ+a3=0,其中:

a1=brRr0+(γ1+εr+dr)+(γ2+dr)>0

a2=brRr0(γ1+εr+2dr)+

2(γ1+εr+dr)(γ2+dr)>0

a3=brRr0(γ1+εr+dr)(γ2+dr)+

且a1a2-a3>0。根據Hurwitz判據得矩陣的特征根均具有負實部，故正平衡點P*局部漸近穩定。

給出系統(2)的Jacobian矩陣對應的第二加性復合矩陣：

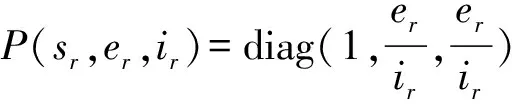
令B=PfP-1+PJ[2]P-1并寫成如下分塊矩陣

其中：

B11=-βrir-2dr-γ1-εr

設(u,v,w)∈R3，定義R3中的向量范數P.P如下：

||(u,v,w)||=max{|u|,|v|,|w|}

記μ(B)是范數P.P的Lozinskl測度,用估值方法得μ(B)≤sup{g1,g2},其中:

g1=μ1(B11)+∣B12∣

g2=μ1(B22)+∣B21∣

μ1(B11)=-βrir-2dr-γ1-εr,

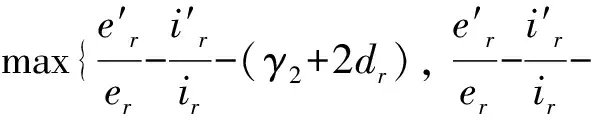
(γ2+2dr+γ1+εr)}

從而得

將式(2)中的第2和第3方程代入上式可得

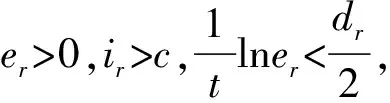
因此系統(2)的正平衡點全局漸近穩定。

2.2 牛群模型穩定性分析

關于牛群的模型如下：

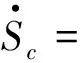
α(Nc-Sc-Ec-Ic)

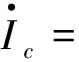
Λ-dcNc-μcIc

上述系統的正向不變集為

Γc={(Sc,Ec,Ic,Vc)∈

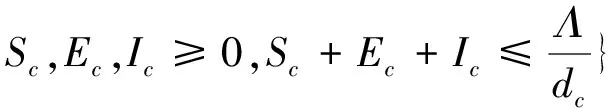
由定理2知：當Rr0>1時，蝙蝠系統中存在唯一穩定的正平衡點，所以僅考慮系統的正平衡點。

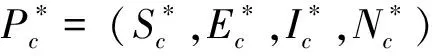
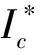
a=μc(p+dc+α)(dc+μc)(dc+εc)>0

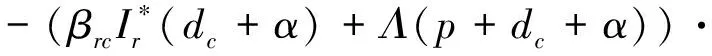
(dc+μc)(dc+εc)<0

根據牛群中正平衡點存在性可得如下閾值

當Rc0=1時，系統僅有1個正平衡點為：

當Rc0>1時，系統有兩個正平衡點：

2.3 系統(1)整體分析

根據下一代矩陣理論，系統(1)在無病平衡點處的基本再生數為

因此，吸血蝙蝠對牛群間狂犬病毒的傳播起決定性作用。當吸血蝙蝠中的基本再生數Rr0<1時，狂犬病不會在牛群中傳播；當Rr0>1且Rc0≥1時，狂犬病會在牛群間傳播，且形成地方病。

3 數值模擬

現階段控制狂犬病在牛群間傳播的最有效措施是給牛群接種疫苗，模擬中取參數γ1=0.05,br=dr=0.01,γ2=0.08,α=0.35,βrc=0.34,βr=0.89,εr=0.9,εc=1,μc=1,Λ=1 000時，對牛接種覆蓋率進行敏感性分析，結果見圖2。

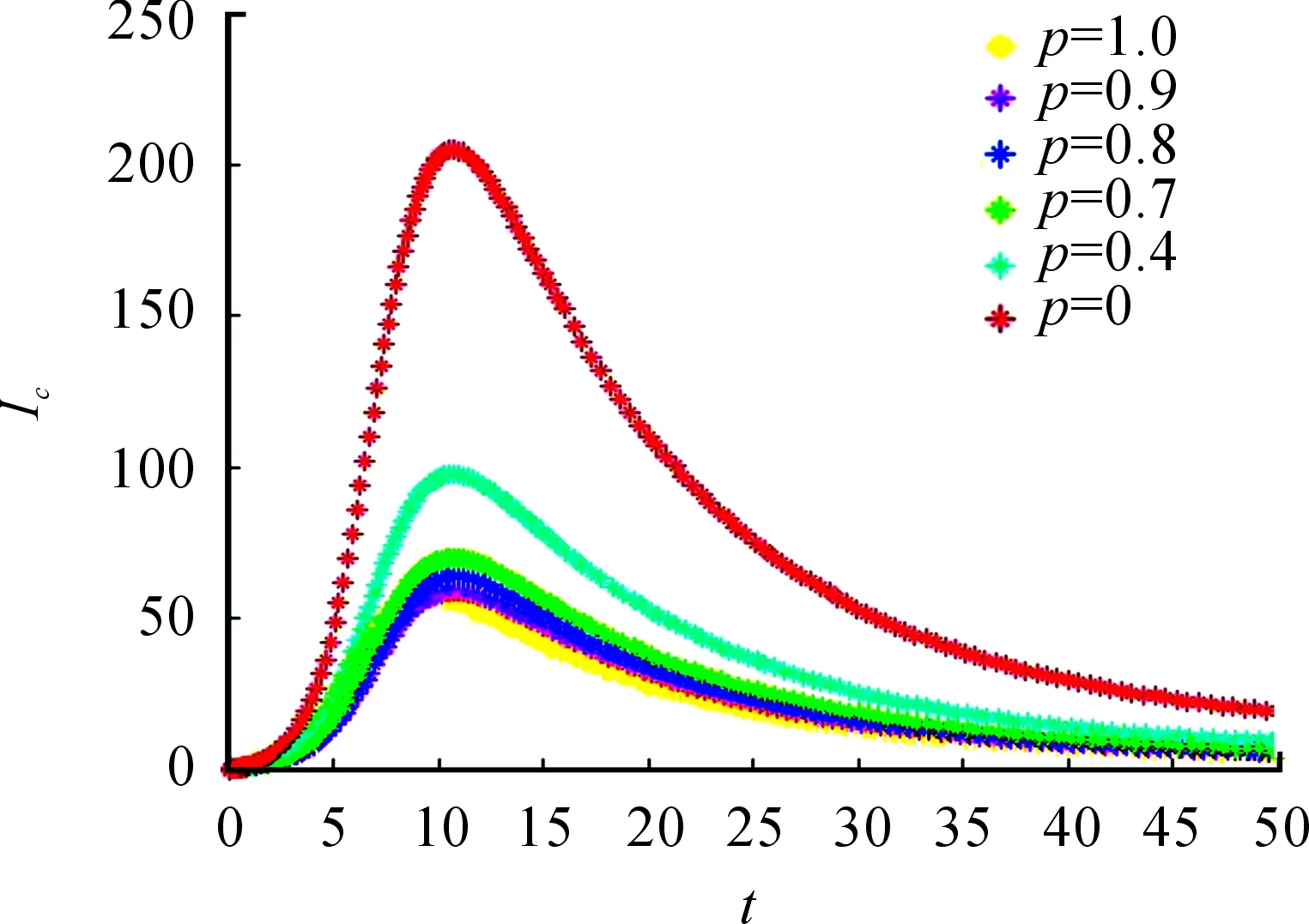
圖2 不同接種率對牛群狂犬病傳播的影響

從圖2中可以看出：當p=0時，狂犬病會在牛群中迅速流行；當采取接種疫苗措施后，染病牛的數量明顯減少。另外，考慮疫苗在牛體內1～1.5年后會失效以及接種疫苗所需成本問題，從圖2可以看出當免疫覆蓋率≥70%時，染病牛的數量變化趨勢幾乎一致。

4 結論

本文以吸血蝙蝠和牛群間狂犬病毒的傳播機理建立數學模型，獲得了模型的閾值并分析了平衡點的穩定性。根據對模型的整體分析知，牛群中狂犬病毒的傳播中吸血蝙蝠起決定性作用。當Rr0>1,Rc0≥1時，狂犬病毒會在牛群中傳播并形成地方病。為降低牛群中狂犬病毒傳播的危害及經濟方面損失，通過對參數敏感性分析可知，當疫苗覆蓋率達到70%以上，可有效預防牛群中狂犬病毒的傳播。