復雜地質條件下煤體-充填體協同控制技術

李 柱，謝 鋒

（1.重慶水利電力職業技術學院，重慶 402160；2.重慶市武隆交通委員會，重慶 408500）

近年來，淺部煤炭資源接近枯竭，因此不得不延伸至深井開采[1-2]。為了減少開采造成的煤炭資源浪費和提高回采準備巷道成型效率，提出了采用充填的方式來解決目前遇到的一系列問題[3-4]。在深部礦井中進行沿空掘巷往往比沿空留巷的維護要簡單些，但其所處力學環境仍比寬煤柱護巷條件下復雜的多[5-7]。雖然我國對沿空掘巷的研究已經很多，也相應的對護巷合理煤柱寬度的留設提出了不同的計算方法，但其應用廣泛性還有待進一步驗證。

1 工程地質概況

冀中能源宣東二礦Ⅲ3302工作面埋深800 m，上臨Ⅲ3303工作面，左為三采區運輸上山。為了保證正常采掘接替，準備在不改變Ⅲ3302工作面通風方式的條件下，采用巷內充填沿空掘巷方式，以保證掘進速度。按照有關規定，煤層瓦斯壓力小于0.74 MPa時或者瓦斯含量小于8 m3/t時，可只進行區域瓦斯驗證，這樣可極大加快掘進速度。

在高瓦斯礦井實施巷內充填沿空掘巷的目的，就是找到合適的掘巷范圍，即可加快掘進速度，解決采掘接替問題，又不違反國家相關的安全規程的規定。在尋找合適沿空掘巷范圍的過程中，防止煤柱過窄導致完全變形破壞，巷內充填沿空掘巷示意圖如圖1。

2 巷內充填工藝

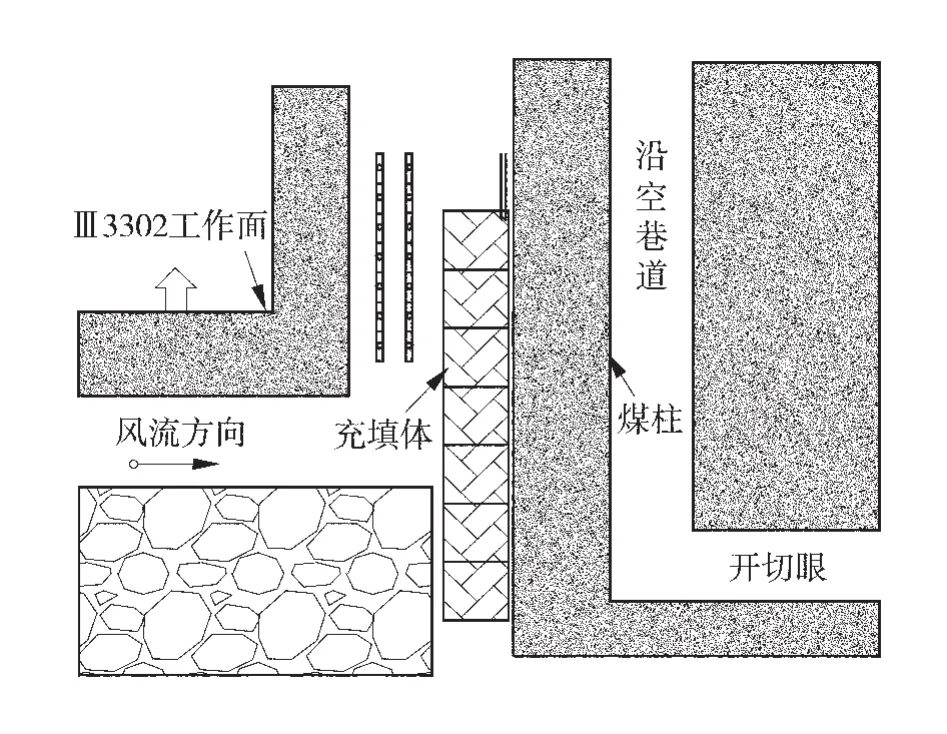
圖1 巷內充填沿空掘巷示意圖

在不改變通風方式、保證工作面正常通風的前提下，充填進度要超前于工作面推進進度。為保證通風斷面，需要增加巷道的寬度至6 m，由于超寬巷道的頂板維護困難，因此為了防止頂板垮落，須用雙排單體液壓支柱配鉸接頂梁進行提前支護。充填體超前充填的進度，可以根據工作面的推進速度V1（與充填速度相同）和切頂所需充填體的強度p共同確定。根據充填體強度發展曲線，可知切頂強度p所對應的充填體養護齡期為D，X為基本頂的極限跨距，則充填體超前工作面距離為Y=D×V1-X。根據宣東二礦Ⅲ3302工作面現場工程地質條件，可以計算出充填體需要超前工作面的充填距離大于45 m。充填體寬度為3 m，約占巷道寬度的1/2。為了保證巷道的穩定性，除了采用錨桿、錨索聯合支護外，利用單體液壓支柱對巷道進行加強支護，控制巷道的變形量。其巷道內充填時的剖面圖如圖2。

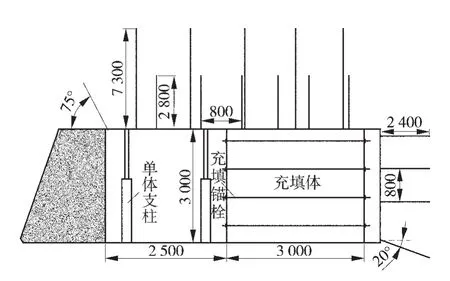
圖2 巷內充填剖面示意圖

根據宣東二號煤礦Ⅲ3302工作面的實際情況，安排在每天的八點檢修班對工作面的巷道進行充填，進行巷內充填的工藝流程如圖3。

3 煤體-充填體力學關系分析

3.1 煤體-充填體接觸面力學分析

由于煤體-充填是1個長度遠遠大于寬度的柱形體，可簡化為平面問題進行分析[8]，煤體-充填體平面結構簡圖如圖4。

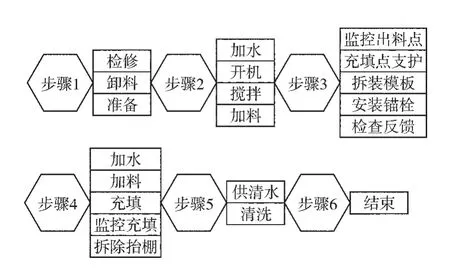
圖3 充填工藝流程示意圖

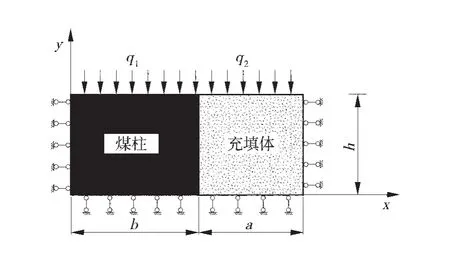
圖4 煤體-充填體平面結構簡圖

煤柱左側受到錨桿的約束，充填體的右側同樣受到了預應力結構的橫向約束，兩邊為水平簡支約束，煤柱-充填體的上部與頂板的接觸面受到頂板的壓力以及頂、底板接觸面的摩擦力限制了煤柱-充填體的水平位移。煤柱-充填體上覆巖層的質量可以簡化為均布載荷q。窄煤柱的寬度為b，充填體寬度為a，煤層厚度為m。煤柱體所承受的載荷為q1，充填體所承受的載荷為q2。在覆巖作用下，煤柱體和充填體之間產生了共同向下的位移，則煤柱體與充填體所承受的平均壓力q1、q2可分別表示為：

式中：E1、E2為煤柱體和充填體的彈性模量。

同時由于煤柱體和充填體處于平衡狀態，根據靜力平衡條件可知：

由于煤柱體和充填體共同承擔上覆巖層的載荷，當充填體承受載荷較大時，煤柱所承受的載荷相對就會變小，穩定性就會越好。它們之間的載荷也可以表示為：

式中：ρ為覆巖平均密度；H為埋藏濃度。

式中：μ1、μ2分別為煤柱體的泊松比、充填體的泊松比。

可以看出，充填體的彈性模量和泊松比越大，其所能夠承受的載荷越大，抵抗變形的能力也就越強。根據胡克定律可以得出煤柱體與充填體之間的相互作用力F0的表達式為：

3.2 煤體-充填體兩幫力學模型

將煤體-充填體看成一個整體，對其兩幫進行受力分析，煤體-充填體力學模型簡圖如圖5。在其煤柱一側煤幫主要約束力來自于巷道錨桿的支護阻力ps，而對于充填體一側主要受力來自采空區垮落矸石對充填體形成的側向擠壓力Fz。煤體-充填體左右兩側橫向受力的差異性由煤柱與頂底板的剪切應力和充填體與頂底板的摩擦阻力來進行平衡。

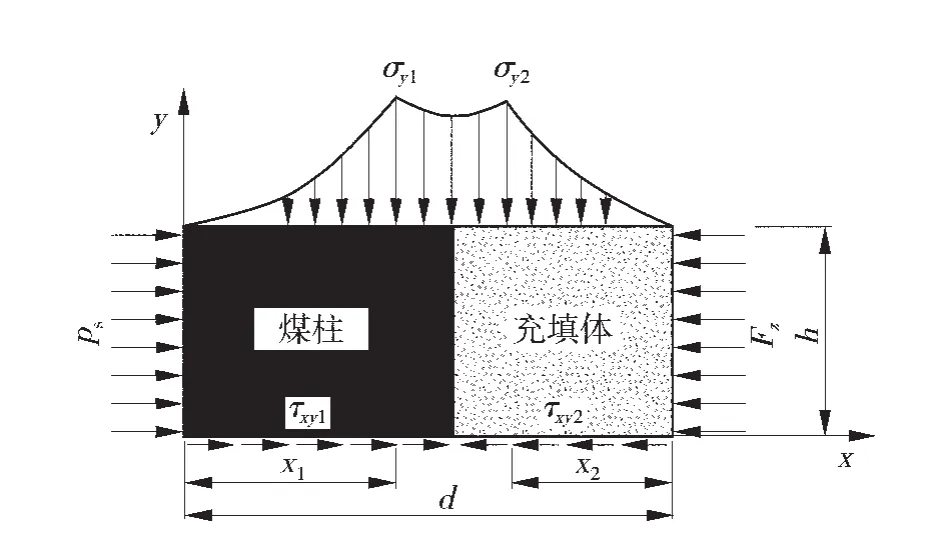
圖5 煤體-充填體力學模型簡圖

其中ps、Fz分別為煤柱左側的錨桿對煤幫的約束力與采空區矸石對充填體的側向擠壓力；τxy為煤柱對于煤層巷道頂底板的剪切應力；f為充填體與頂底板之間的摩擦阻力；x1、x2分別為煤柱與充填體的應力極限平衡區寬度；σy1、σy2分別是煤柱與充填體的支承壓力峰值也即極限強度。其中煤柱的受力模型如圖6[9-10]。

對該模型進行求解，其中σy1＝KρgH，K為煤體的應力集中系數，C0、φ0分別為煤體的黏聚力和內摩擦角。利用沿空掘巷實體煤幫應力極限平衡區的計算公式可以推導出模型中x1的表達式：

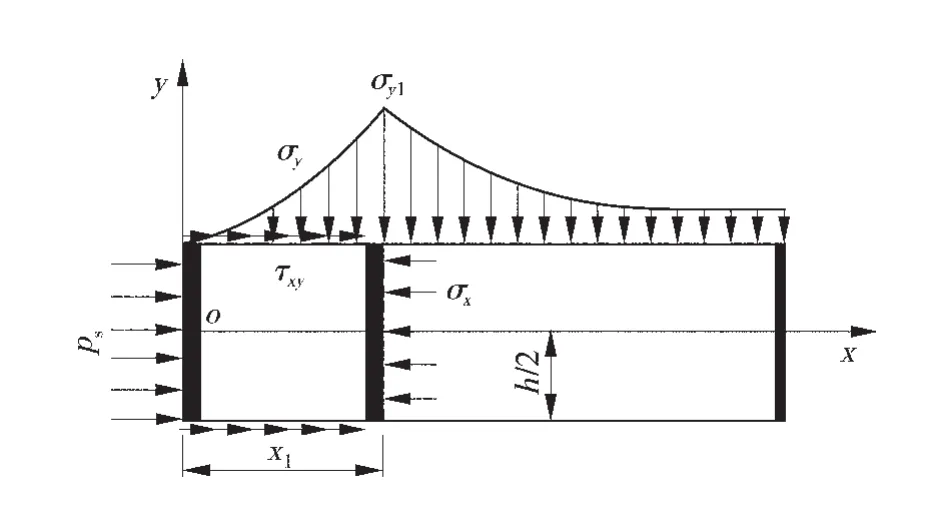
圖6 煤柱受力模型簡圖

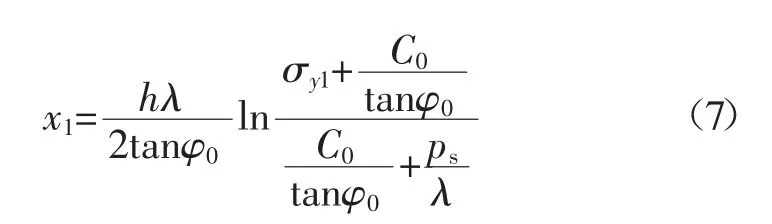
式中：λ為側壓系數；h為巷道高度。

對于沿空掘巷巷幫煤柱應力極限平衡區內任意一點的應力表達式為：

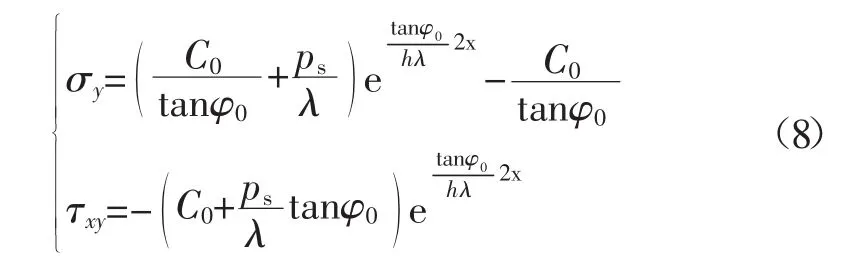
假設沿空掘巷充填體的應力集中系數為Kc，富裕系數為A；則對于充填體在水平方向的應力σxc的表達式為：

充填體的受力模型如圖7。

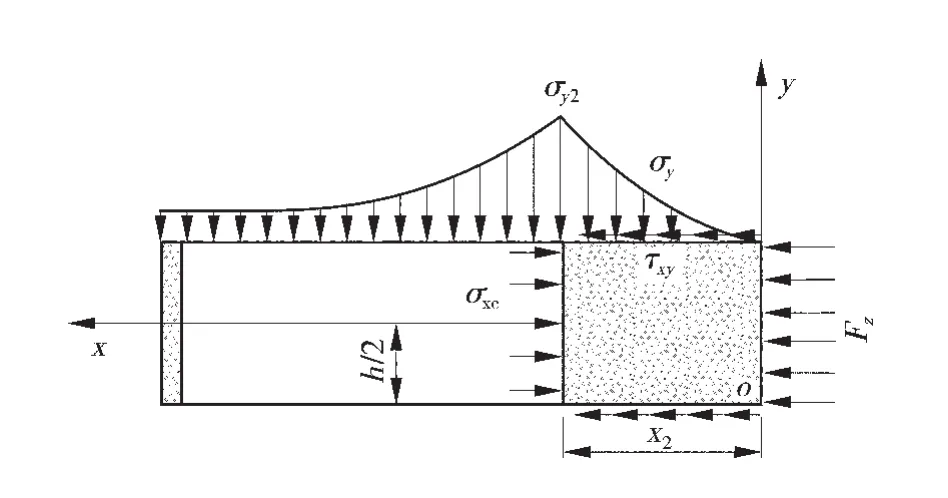
圖7 充填體受力模型簡圖

對該模型進行求解，利用應力極限平衡區的計算公式可以得出充填體的應力極限平衡區域的x2的表達式：

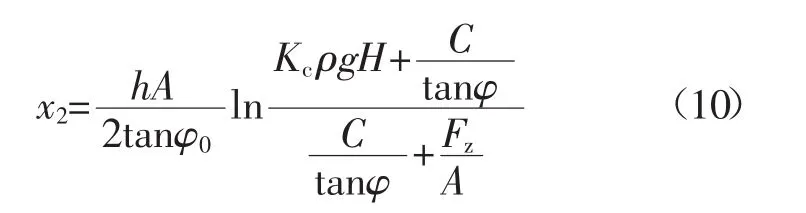
式中：C、φ分別為充填材料的黏聚力和內摩擦角。

充填體采空區側的極限平衡區內任意一點的應力表達式：

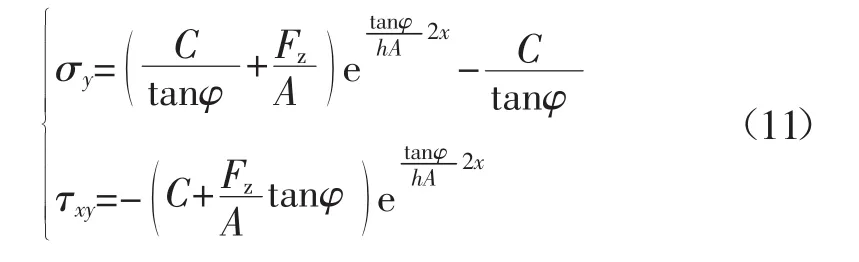
3.3 煤體-充填體的影響因素分析

Ⅲ3煤層埋深H=800 m，煤體的黏聚力C0=2.5 MPa，巷道高度h=3 m，應力集中系數K=2，內摩擦角 φ0=30°，側壓系數 λ=1.8，覆巖的平均密度 ρ=2.2 t/m3，煤體的彈性模量E=2 400 MPa，其煤層的性質、埋深、巷道的設計寬度都已固定，因此研究影響煤體-充填體的塑性區寬度影響因素時，只考慮支護阻力、充填體強度等對煤體-充填體的塑性區寬度的影響。不同充填體強度的設置參數見表1。

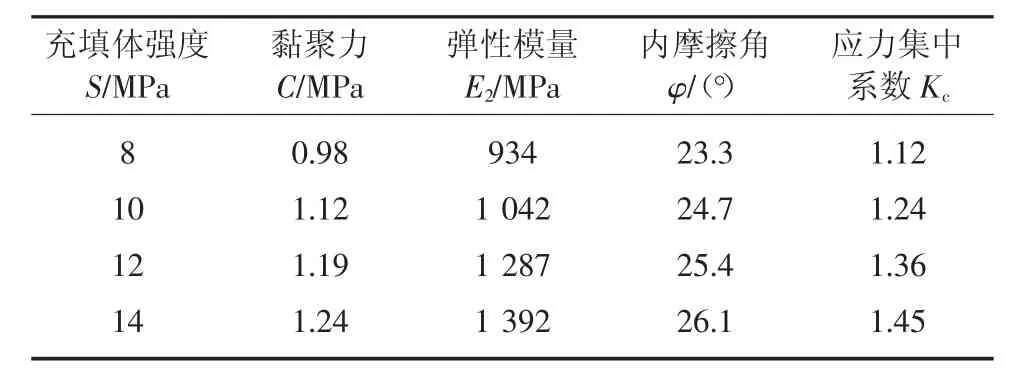
表1 不同強度充填體的力學參數

根據式（7）和式（10）可分別計算出充填體側不同強度大小和煤體側不同強度大小時塑性區寬度的變化情況（圖8）。

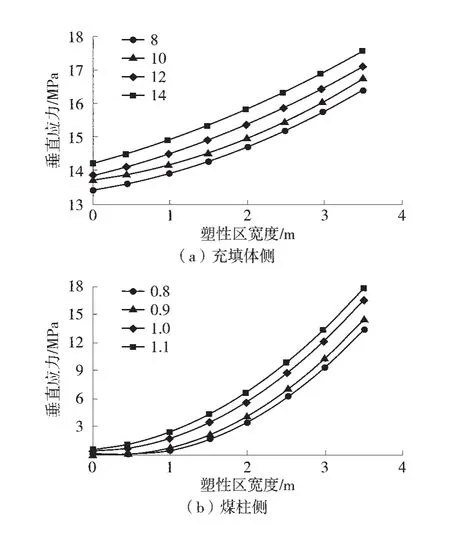
圖8 煤體-充填體兩側塑性區寬度分布規律

由圖8（a）可知，隨著充填體強度的上升，塑性區的寬度也出現了明顯的下降。可見通過改善充填體自身強度可以在一定程度上降低塑性區寬度，增加支撐力，改善沿空掘巷巷道的穩定性。由圖8（b）可知，煤柱側在支護強度改變時，塑性區寬度也隨之發生改變，支護強度越大越有利于巷道圍巖的穩定性，因此在進行沿空掘巷時，合理設計巷道支護方案，對控制巷道圍巖的變形破壞有一定的作用。

基于Kastner公式，考慮煤層瓦斯影響得到高瓦斯煤層巷道的圍巖塑性區半徑R的計算如式（1）。

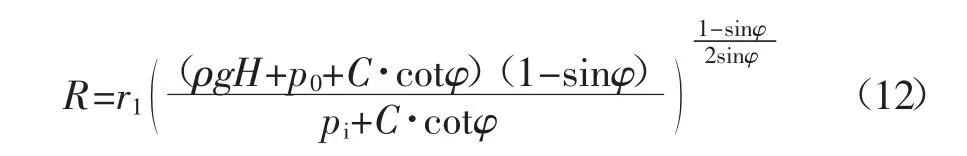
式中：r1為巷道半徑；pi為平均支護阻力；p0為瓦斯壓力。

針對宣東二號煤礦沿空掘巷工作面煤層參數，工作面埋深800 m，覆巖平均密度為2.5 t/m3，巷道半徑r1為2 m，瓦斯壓力p0為2 MPa，平均支護阻力pi為1 MPa，煤體黏聚力C為1.5 MPa，內摩擦角φ為30°。為了簡化理論計算，假設巷道處于靜水應力場，巷道塑性區與彈性區交界的邊緣應力可表示為ρgH+p0。

塑性區半徑與瓦斯壓力的關系如圖9。由圖9可知，隨著瓦斯壓力越大，塑性區半徑范圍也隨之增大，因此在工程實踐中進行沿空掘巷時，需要對煤層內瓦斯壓力進行監測與分析，在確定沿空掘巷煤柱留設寬度時，應該對瓦斯壓力對煤體所產生的影響進行綜合考慮。

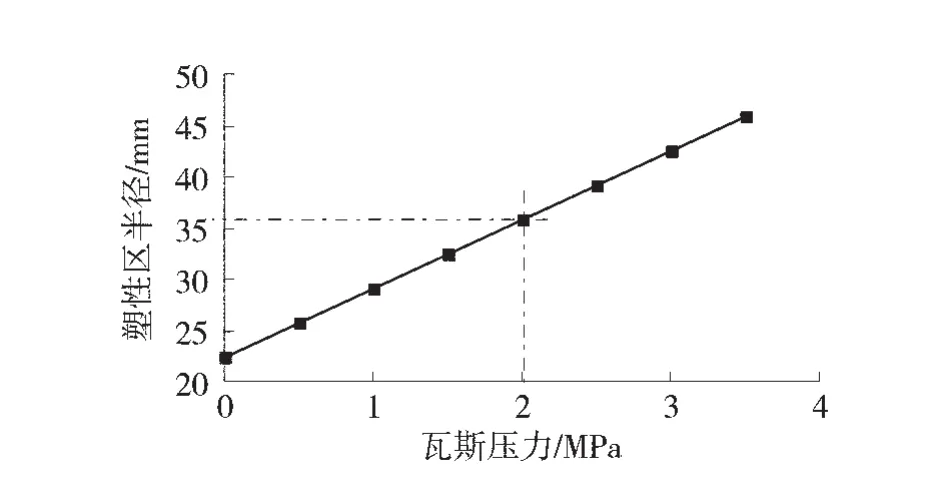
圖9 塑性區半徑與瓦斯壓力的關系

根據Ⅲ3煤層地質情況，并基于式（7）和式（10）可計算求解出煤體-充填體協同護巷時巷道側煤柱的塑性區寬度x1=1.82 m，采空側充填體的塑性區寬度x2=2.11 m，瓦斯壓力影響塑性區半徑R=0.36 m。考到到煤體-充填體的穩定性，可按照（x1＋x2＋R）的30%～50%確定中間彈性核區的寬度x3，在此按照40%確定為x3=1.72 m，因此可以確定煤體-充填體的總寬度為W=6.01 m。

4 工程應用

為了檢驗支護效果，在超前工作面60 m位置處設置礦壓監測點，對巷道圍巖變形情況進行監測。相鄰工作面回采期間巷道圍巖變形情況如圖10。由圖10中監測數據可知：工作面回采期間，巷道頂、底板移近量分別為380 mm和315 mm，煤柱幫和實體煤幫移近量分別為352 mm和338 mm，圍巖整體變形在可控范圍內，沒有發生失穩現象，說明煤體-充填體協同護巷方案達到了預期的效果。

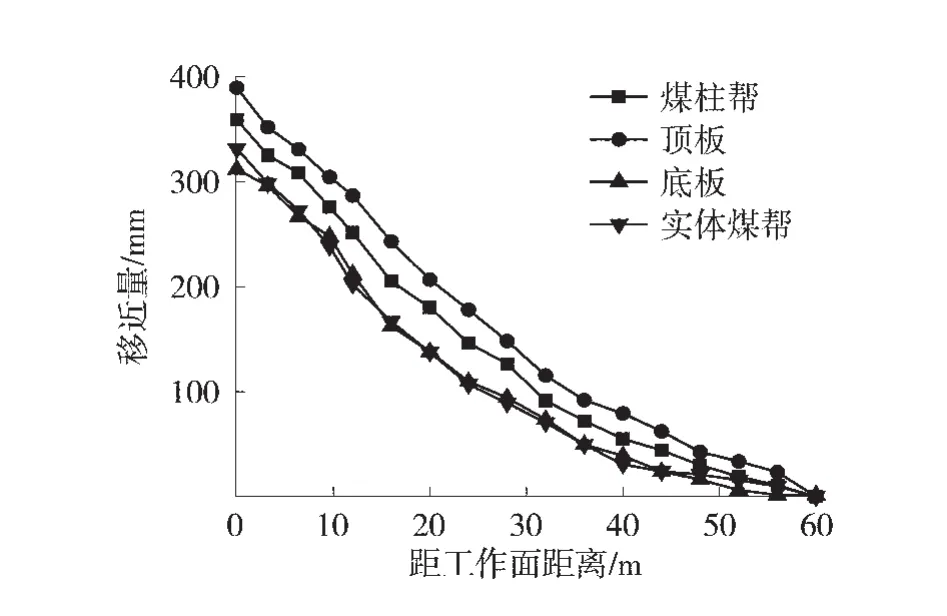
圖10 相鄰工作面回采期間巷道圍巖變形情況

5 結論

1）根據宣東二礦Ⅲ3302工作面現場工程地質條件，計算出充填體超前工作面的充填距離≥45 m，充填體的寬度為3 m，約占巷道寬度的1/2。

2）通過建立煤體-充填體力學模型對其進行計算分析，得知通過改善充填體自身強度和支護強度有利于巷道圍巖的穩定性，并根據Ⅲ3煤層地質情況可知受瓦斯壓力影響下煤體-充填體的最優寬度為6.01 m。

3）現場礦壓觀測結果表明，鄰近工作面回采過程中，煤體-充填體協同護巷下巷道頂、底板移近量分別為380 mm和315 mm，煤柱幫和實體煤幫移近量分別為352 mm和338 mm，圍巖整體變形在可控范圍內。