爆破動荷載作用下深埋隧道失穩破壞模擬研究

張 蘭 ，孫中光 ，2

（1.中煤科工集團重慶研究院有限公司，重慶400039；2.重慶大學，重慶 400044）

20世紀80年代以來，我國的隧道建設技術取得了重大的突破，建成了一批斷面大、埋藏深、距離長的復雜隧道工程，積累了大量的工程建設經驗。目前深埋隧道的施工方法主要采用鉆爆法，鉆爆法施工成本低，技術較為成熟，對不同地質條件適應性強[1]。但爆破過程容易引起開挖區圍巖性質的劣化，尤其是在近距離穿越的隧道工程中，新建隧道的爆破荷載往往會對既有隧道結構造成影響，導致工程結構的失穩破壞[2]。

目前，對于深埋隧道工程的失穩破壞研究主要考慮了巖體自身軟弱結構面和高地應力、高溫作用。趙景彭[3]研究了裂隙產狀對深埋隧道穩定性的影響。張志強等[4]將節理巖體隧道的擾動區分為剪切滑移區、節理張開區和脫落區，提出以剪切滑移區面積作為深埋隧道穩定性的量化指標。呂慶等[5]從圍巖結構特征和地應力環境方面預測了蒼嶺深埋特長隧道的巖爆情況。陳國慶等[6]研究了溫度場和應力場耦合作用下深埋硬巖隧道開挖的力學響應，并預測了巖爆烈度。事實上，爆破開挖、斷層滑動等施加的動荷載同樣是隧道失穩破裂不可忽視的因素之一。非穩定平衡狀態下的巖體，在受到爆破等動荷載作用時可能突然失穩，引發巖爆災害[7-8]。國內外學者采用理論分析和數值計算方法研究了動荷載對隧道(或巷道)工程結構的影響。張露晨等[9]采用關鍵塊體理論分析隧道圍巖穩定性時，考慮了爆破震動和地震動荷載的作用，計算結果與工程實際更加吻合。Amin等[10]應用Abaqus軟件模擬了含原生節理隧道在動靜荷載共同作用下，破裂區巖塊的速度和能量特征。劉思妤和徐則民[11]開展了一系列動靜應力耦合的深埋長大隧洞巖爆災害控制研究，認為巖爆的發生必須滿足3個必要條件，此外巖爆的控制應該綜合考慮動靜應力的耦合效應。

采用爆破的方法進行深埋隧道失穩破壞的室內或模型試驗研究常常受到試驗條件、試驗人員爆破技術以及試驗原料等的限制，而數值軟件具有可操作強、可重復性高以及低成本等特點使得其在研究爆破等動荷載方面具有明顯的優勢，因此，在前人的研究基礎上，引入顆粒離散元數值軟件PFC，開展爆破動荷載作用下深埋隧道失穩破壞的數值模擬。通過分析動態擾動過程隧道圍巖的微裂紋和碎石塊體積等指標的變化規律，揭示隧道巖體失穩破壞機制，以期為深埋隧道的支護技術和災害預報研究提供可靠的理論依據。

1 模型建立

1.1 隧道開挖模擬

隧道顆粒流模型示意圖如圖1。取含隧道的某一巖體斷面作為研究對象。引入離散元數值計算軟件PFC，在四面墻體(wall)固定的狀態下，生成尺寸為25 m×25 m的黏結顆粒體模型(BPM)。通過邊界加載的方式模擬初始地應力場，首先刪除頂面和左側面的剛性墻體，并在模型臨空位置分別構建長度為25 m的長條形塊體(clump)，然后給長條形塊體施加指向模型內部的豎向應力σ1和橫向應力σ3，直到模型平衡。自模型中央開挖直徑為6 m的圓形隧道孔洞，即刪除該范圍內的顆粒體，待模型再次平衡時，清除所有顆粒的位移和速度。

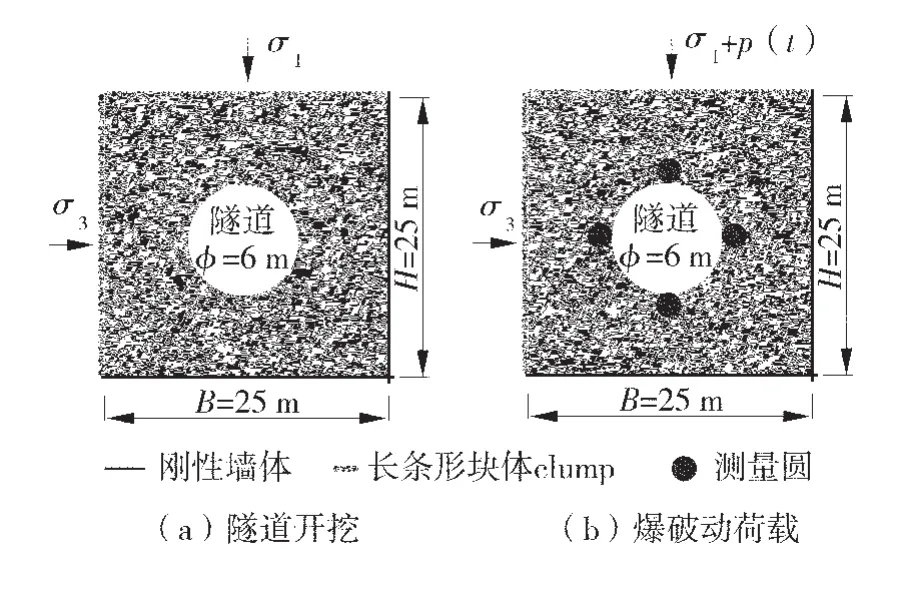
圖1 隧道顆粒流模型示意圖

1.2 細觀參數確定

在數值計算之前，需要對模型的細觀結構參數進行標定。隧道圍巖巖體采用了文獻[7]中結構完整、質地均勻的砂巖體。砂巖試樣的力學參數見表1。通過對單軸壓縮數值試驗的細觀參數進行敏感性分析，發現宏觀力學參數泊松比受接觸的法向與切向剛度之比影響顯著，而彈性模量和單軸抗壓強度主要與有效模量和黏結拉伸強度有關。據此反復調整細觀參數，最終得到1組隧道圍巖體模型細觀力學參數（表2）。

表1 砂巖物理力學參數

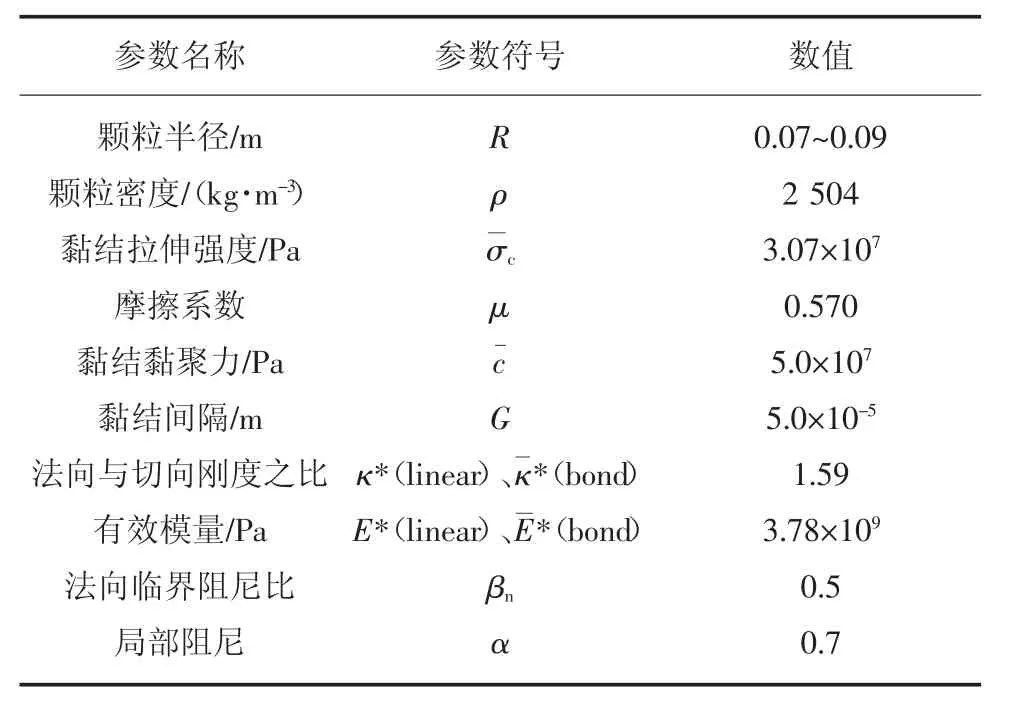
表2 顆粒流細觀力學參數

式中：pd為等效均布荷載，Pa；r為炮孔半徑，m；l為同排炮孔的孔間距，m；p（t）為單個炮孔爆炸時產生的動荷載，Pa。

假設在隧道上方一定距離的硐室開挖，排間距為1.25 m的同排炮孔起爆產生爆破動荷載。為了便于計算，采用上述方法將隧道上方的爆破動荷載簡化為模型頂面隨時間變化的均布荷載。

爆破動荷載時程曲線可近似處理成三角形、指數型和拋物線等形式[10-16]。采用三角形形式，即包含線性變化的上升階段和下降階段。爆破荷載的持續時間與炮孔堵塞物、炮腔膨脹等因素有關，通常認為該持續時間為1.0×10-6～0.1 s[13-14]。考慮到顆粒離

1.3 爆破動荷載模擬

爆破動荷載是指由爆炸引起的作用于炮孔壁上隨時間劇烈變化的瞬時荷載。文獻[12-13]中將同排炮孔的爆破荷載等效為炮孔連心線與炮孔軸線控制平面上的均布荷載，由下列公式進行換算：散元與有限元等連續介質力學方法相比，應力波在黏結顆粒體內的傳遞過程較為緩慢，因而選取爆破動荷載的升壓時間5 ms，正壓作用時間30 ms，爆破動荷載時程曲線如圖2。

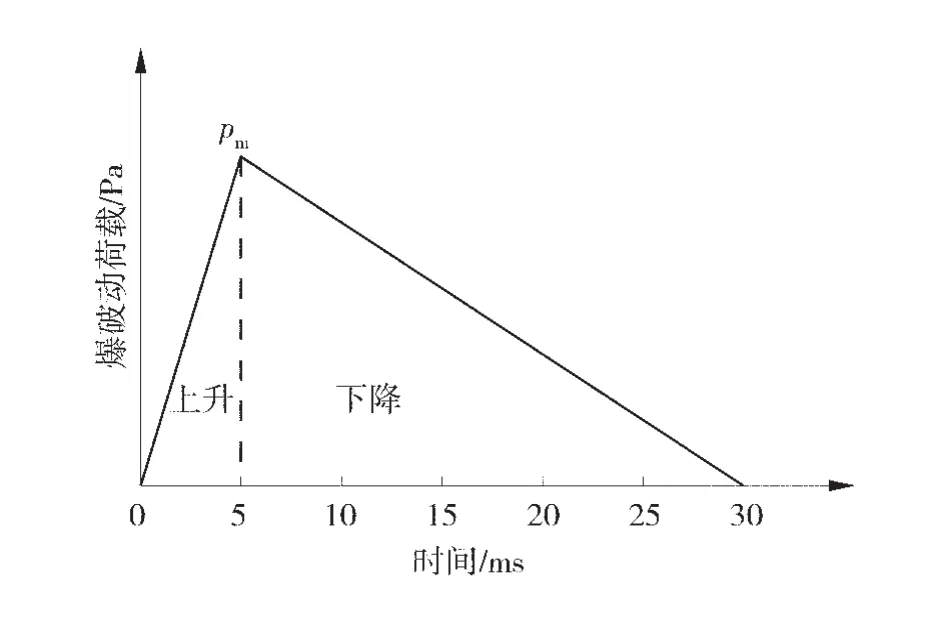
圖2 爆破動荷載時程曲線

單個炮孔爆炸產生的三角形荷載為：

式中：f（t）為反映爆破荷載隨時間變化的函數，可通過升壓時間和正壓時間進行計算；pm為爆破荷載峰值，主要與炸藥的性質有關。

在不耦合連續裝藥條件下，pm通過式（2）計算[12]：

式中：D 為炸藥爆速，m/s；ρc為裝藥密度，kg/m3；kc為不耦合系數；η為孔壁壓力受爆轟氣體影響的擴大倍數，取η=9。

因此，等效均布荷載可以寫成：

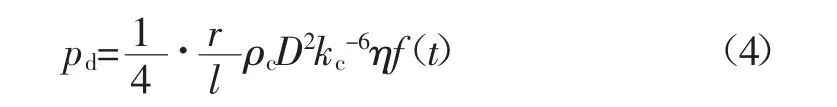
參考文獻[12]中2號巖石乳化炸藥參數，炸藥的爆速3 500 m/s，裝藥密度1 000 kg/m3，炮孔半徑0.055 m，裝藥不耦合系數為1.447。經計算得等效均布荷載 Pd=1.38 ×108。

假設側壓力系數為1，對于選定的埋藏深度，由下列公式計算豎向應力σ1和橫向應力σ3。

式中：H為埋藏深度，m。

2 模擬結果

對隧道進行受力分析可知，隧道不僅承受隨時間變化的爆破動荷載，而且始終位于地應力條件下。地應力與隧道等地下工程的穩定性密切相關，它是引起圍巖變形破壞的主要作用力。隨著埋深的增加，地應力對隧道圍巖的穩定性影響顯著。爆破動荷載作為隧道結構的一種附加應力，持續的時間極短。爆破發生后隧道沒有立刻達到穩定狀態，而是在地應力的作用下經過一段時間才達到平衡。因此，對比分析了爆破荷載完成時的隧道破裂特征與爆破荷載完成后隧道重新平衡時的特征。

模擬過程中，開挖不同埋深的隧道，隧道未出現明顯的損傷區，很快達到穩定狀態，說明開挖以后重新分布的圍巖應力沒有超過結構完整的砂巖巖體強度。隨后施加爆破動荷載，引起隧道的變形破壞。爆破荷載作用完成時與隧道重新平衡時微裂紋分布圖如圖3。

圖3 爆破荷載作用完成時與隧道重新平衡時微裂紋分布圖

在模型頂面同等的爆破荷載影響下，隨著埋深的增加，隧道巖體內微裂紋區域擴長，損傷破壞主要集中于隧道的兩幫，而在底板并沒有出現裂紋；右側的微裂紋由側壁向頂板發展，在離壁面一定深度范圍內形成弧形的貫穿裂紋。模型頂面炸藥起爆后，爆炸應力波使得隧道硐周的應力集中，超過巖體的強度，因此在爆破荷載作用完成時，出現了不同程度的裂紋損傷，但是幾乎沒有巖石剝落或彈射的現象。當模型重新平衡時，可觀察到隧道巖體的損傷程度加劇，主要表現在左側的裂隙巖體開始剝離，甚至發生巖爆現象，尤其是在埋深達到800 m時，剝離、彈射的巖塊使得側壁趨于形成“V”型的爆坑；右側的裂隙巖體除了出現剝離、彈射的現象以外，還可以觀察到延伸至頂板的弧形裂紋繼續擴展貫穿頂板壁面，形成宏觀的張開型裂紋。由此可見，爆破荷載使原本穩定的隧道圍巖產生節理裂隙，而在高地應力的持續作用下，節理巖體的損傷程度將會加劇，因而進入非穩定破壞過程。

為了進一步分析隧道巖體損傷破裂程度，統計以隧道中心為圓心、6 m距離為半徑的圓形巖體范圍內的微裂紋數和碎石塊的總體積（圖4、圖5）。

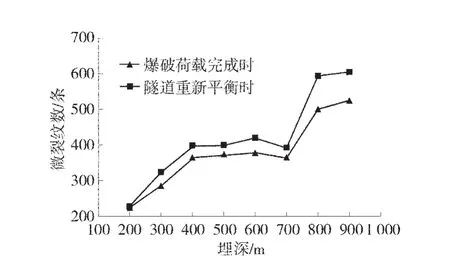
圖4 微裂紋個數

圖5 碎石塊體積

從圖4來看，在爆破荷載和地應力的共同作用下，隧道硐周微裂紋的個數隨埋深的增加呈增長趨勢，當隧道埋深為200～700 m時，微裂紋數量的增長幅度相對較小，當埋深達到800 m時，微裂紋的數量急劇上升,說明埋深條件是影響穩定性的一個重要因素，一旦超過隧道自穩所允許的深度后，微裂紋個數將出現階躍式增長。圖4中的碎石塊是指脫離母巖體獨立出來的塊石體。在爆破荷載作用完成時，統計的碎石塊總體積變化并不明顯，主要是在埋深達到800 m以后出現大幅增長；當隧道模型重新平衡時，埋深為200～400 m的碎石塊體積隨埋深的增加而增加，500 m時開始下降，而在600 m之后再次呈上升趨勢，且在800 m時達到最大，總體積為0.42 m3。圖5中碎石塊總體積的增長率是指隧道重新平衡時的碎石塊體積相比爆破荷載完成時的體積增長率，從圖中來看，除了埋深為500 m時，隧道再次平衡時碎石總體積相比爆破荷載完成時沒有變化，其它埋深情況碎塊體積增長率基本達到100%以上，這一現象同樣說明爆破動荷載主要造成隧道圍巖性質的劣化，而在高地應力的持續作用下，圍巖的破壞程度將會加劇，甚至引發巖爆等地質災害。因此，在深埋隧道臨近位置爆破時，應當及時對開挖后的隧道進行有效的支護處理，做好巖爆等災害的實時監測工作。

3 結論

1）在距離隧道一定高度的頂面施加爆破動荷載，隨著埋深的增加，圍巖損傷程度越嚴重，損傷集中于隧道的兩幫，并逐漸由隧道右側向頂板發展。當達到一定深度后，微破裂的數量呈階躍式增長，隧道壁面可能出現巖塊剝離和彈射等現象。

2）在距離深埋隧道一定高度的位置爆破時，隧道的失穩破壞是由爆破荷載和地應力共同造成的，爆破荷載主要使隧道圍巖產生損傷裂紋，而在地應力的持續作用下，可能引起巖塊的剝離和彈射現象。