鶴壁市城鎮體系空間結構優化

李銘輝，竇富國，于 壯，張合兵，邵河順

（1.河南理工大學測繪與國土信息工程學院，河南焦作 454000；2.河南省鶴壁市國土資源監察支隊，河南鶴壁 458000）

城鎮體系是指在一定地域范圍內，以中心城市為核心，由一系列不同等級規模、不同職能分工、相互緊密聯系的城鎮組成的復合有機整體［1］。城鎮體系在推進區域城鎮化，促進資源合理利用、產業結構優化調整和社會經濟快速協調可持續發展方面起著重要作用。城鎮體系空間結構是區域發展的骨架，其特征是區域政治、經濟、文化等因素長期發展演變，在地域空間上的綜合表現，從理論上來講，城鎮體系空間結構不可能達到完全合理的狀態，因此研究區域城鎮體系空間結構特征，對于了解區域城鎮體系經濟發展特征，促進區域城鎮體系功能和結構的優化，實現區域經濟的可持續發展具有重大意義。目前，國內學者對于城鎮體系的研究多集中在規模等級研究［2-4］、空間結構特征及其演變規律研究［5-8］、影響因素研究［9-11］、城鎮體系系統同其他系統的耦合機制研究［12-14］等方面。在研究方法上，多基于分形理論構建研究模型，這是因為城鎮體系是一種復雜的非線性系統，具有無標度性，不能用確切的單位去計量描述，其空間分布具有自相似性，無規律可循。而分形理論可以很好地揭示城鎮體系的無標度性和自相似性，對于描述城鎮體系空間結構的幾何分布特征具有良好的效果。目前，基于分形理論的城鎮體系空間結構研究多采用行政區幾何中心進行測算［15-16］，或者通過遙感技術（remote sensing，簡稱RS）獲取研究區城鎮邊界幾何中心進行測算［17-18］，均存在對城鎮分形中心把握不夠準確的問題。本研究將基于年度土地利用變更調查數據，精準提取鄉鎮建設用地邊界，確定其分形幾何中心，并測算鶴壁市縣（區）城鎮聚集維數和鶴壁市關聯維數，在此基礎上通過場強模型識別縣（區）中心城鎮輻射影響范圍，定量描述鶴壁市城鎮體系空間結構分布特征，對優化鶴壁市城鎮體系空間結構，促進鶴壁市經濟協調可持續發展具有重大意義。

1 研究區概況與數據來源

1.1 研究區概況

鶴壁市位于河南省北部，太行山東麓與華北平原交界處（113°59′～114°46′E、35°26′～36°53′N），東西北與安陽市接壤，南與新鄉市相鄰，南北寬約67 km，東西長約69 km，總面積2 140.43 km2。全市轄3區（鶴山區、山城區、淇濱區）2縣（浚縣、淇縣）。鶴壁市境內自然資源豐富，已探明30多種礦藏，屬國家能源重化工基地和黃淮海平原農業綜合開發區。自1957年建市以來，城市發展“緣礦而建”，隨著煤炭資源的不斷開采及消耗，鶴壁市主城區先后經歷了3次歷史變遷，形成了現在典型的資源型城市城鎮體系空間結構，但也遺留下許多歷史發展問題，如城區不聚集、土地利用集約化程度低、環境污染情況嚴重等，嚴重制約了鶴壁市社會經濟的發展。

1.2 數據來源

本研究所采用的數據來源于鶴壁市國土資源局提供的2014年度土地利用變更調查數據庫、鶴壁市土地利用總體規劃數據庫（2009—2020）和統計局提供的2015年鶴壁市統計年鑒。首先提取鶴壁市各個鄉鎮建設用地邊界，并對1 hm2以下碎小圖斑進行剔除，縣（區）城鎮邊界采用鶴壁市土地利用總體規劃（2009—2020）確定的縣（區）中心城區；然后利用ArcGIS空間分析工具確定各個城鎮建設用地幾何中心，并計算得到各個城鎮點之間的歐式距離。

2 城鎮體系空間結構分形研究方法

2.1 空間聚集分析

假定城鎮體系內各結構按照某種自相似規則圍繞中心城鎮呈凝聚態分布，且分形體在各個方向是均勻變化的，則可以通過幾何測度關系確定以r為半徑的圓形區域內的城鎮數目N（r）［19］，其與對應的半徑存在一定的關系：

式中：D為空間聚集分維數；r為回旋半徑；N（r）是以中心城市為圓心、r為半徑的圓形區域內的城鎮個數。目前上式經過證明成立［20］。為了消除半徑r的單位不同帶來的誤差，定義平均半徑R來代替r：

式中：Rs為平均半徑；S為區域內城鎮點數量；ri是從中心點到第i個點之間的距離。上述公式的值代表由S個城鎮點組成聚集區域的平均半徑。平均半徑與城鎮數量的分維關系有：

通過線性回歸即可計算分形維數D，D的含義可以解釋為城鎮體系分布從中心城鎮向四周的聚集衰減程度，通常計算得到D值應該在0～2之間。當D＞2時，城鎮體系內城鎮的分布密度沿著中心城鎮向四周的方向遞增，城鎮沿著半徑方向均勻散開呈離散狀態分布；當D＝2時，各個城鎮圍繞著中心城鎮呈均勻態分布，沒有聚集特征；當D＜2時，各個城鎮的分布在空間上圍繞著中心城鎮表現出聚集態，城鎮的分布密度沿著中心城鎮向周邊方向逐漸減少，且D越小，周圍城鎮聚集程度越高。

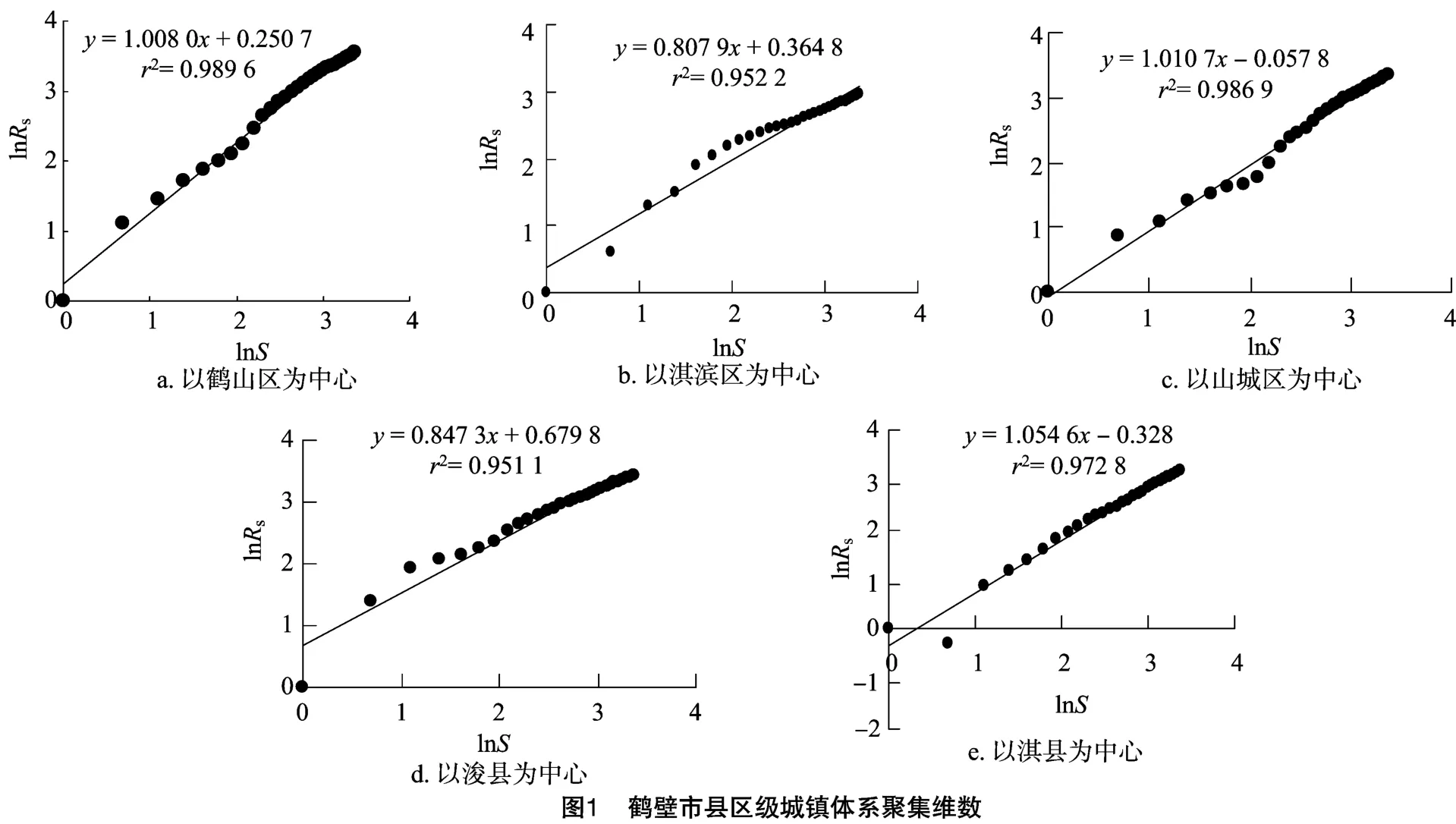
基于以上模型，本研究分別以鶴壁市縣（區）中心城區為中心城鎮，計算鶴壁市城鎮體系聚集維數。分別提取縣（區）中心城鎮幾何中心，通過ArcGIS分析工具計算其到其他28個城鎮的歐式距離，然后通過公式（2）計算得到平均半徑（表1），再對點（Rs，S）取雙對數，用（ln-ln）圖表示（圖1），對其進行回歸分析。

表1 鶴壁市城鎮體系平均半徑

2.2 空間關聯分析

城鎮體系空間結構的關聯性分形通常采用空間關聯維數進行研究。其模型為

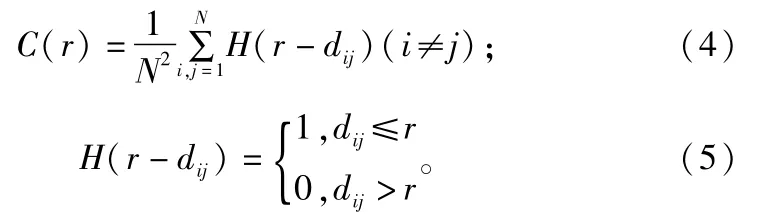
式中：r為距離標度；C（r）為根據給定距離r所選取的城鎮的數目；dij為城鎮體系內第i個城鎮與第j個城鎮間的直線距離；H（r）為Heaviside階躍函數。根據城鎮體系空間分布的分形特征，有

式中：D為關聯維數，其地理意義反映了城鎮之間相互影響的規律性，為使計算方便，可令N（r）＝C（r）N2，N（r）為dij≤r的城鎮數目［17］，那么式（6）可改寫為：

通過線性回歸可計算關聯維數D，D值一般在0～2之間。當D取值趨近0，表明該地區內各個城鎮之間關聯緊密，空間相互作用強，各個城鎮分布高度集中于某地；當取值D趨近1，表明各個城鎮沿地理線集中分布，如河流、鐵路、海岸等；當取值D趨近2，各個城鎮之間關聯不緊密，空間相互作用弱，城鎮空間布局均勻且分散。

基于以上模型，以鶴壁市29個城鎮為對象，計算整體關聯維數。將29個城鎮間兩兩歐式距離dij列成表格（表2），這實際上是一個對稱矩陣，這里只列出半角，但計算城鎮總點數時，必須考慮滿陣的數據（即N2＝29×29）。取標度r＝55、50、45、40、35、…、5（步長Δr＝5 km），對應的N（r）＝841、821、…、51，于是得到點列［r，N（r）］（表3），再對點列［r，N（r）］取對數，在坐標圖中繪制，可以看出，點列呈線性分布（圖2），并對其進行回歸分析。

3 城鎮體系中心城鎮輻射范圍識別研究方法

中心城鎮作為區域城鎮空間結構的核心，對周圍城鎮的發展具有不可替代的影響作用，其影響力與自身城鎮規模成正比，與周圍城鎮距離成反比，并呈現距離衰減規律，最終與其他中心城鎮之間的影響力達到平衡，在平衡處即為斷裂點，斷裂點處2個城鎮之間的相互作用強度即為場強。

3.1 斷裂點模型

式中：Di為城市i到斷裂點的距離；Dij為i、j2個城市間距離；Mi、Mj為2個城市的綜合規模指數，i代表起點城市，j代表終點城市。

3.2 場強模型

式中：Fik為城市i在斷裂點k的場強大小；Dik為城市i到斷裂點k的距離；Mi同上。

3.3 輻射半徑模型

式中：Dr為城市i的輻射范圍；F為所選擇確定的邊界場強；Mi同上。

3.4 中心城鎮輻射范圍識別

根據既有研究成果，選擇中心城鎮非農人口數、城鄉建設用地面積和地區生產總值的幾何平均數作為城市綜合規模指數［21］，具體計算公式為

由于淇濱區發展時間尚短，根據2014年地區生產總值，淇濱區地區生產總值僅排名第3位，但與2013年相比淇濱區增速排名第1，并且淇濱區作為鶴壁市政治經濟文化中心，具有巨大的發展潛力，故選取淇濱區作為鶴壁市經濟中心，考慮到市域尺度內，交通距離影響較小，故將Dij設定為城鎮之間的直線距離，計算結果如表4所示。

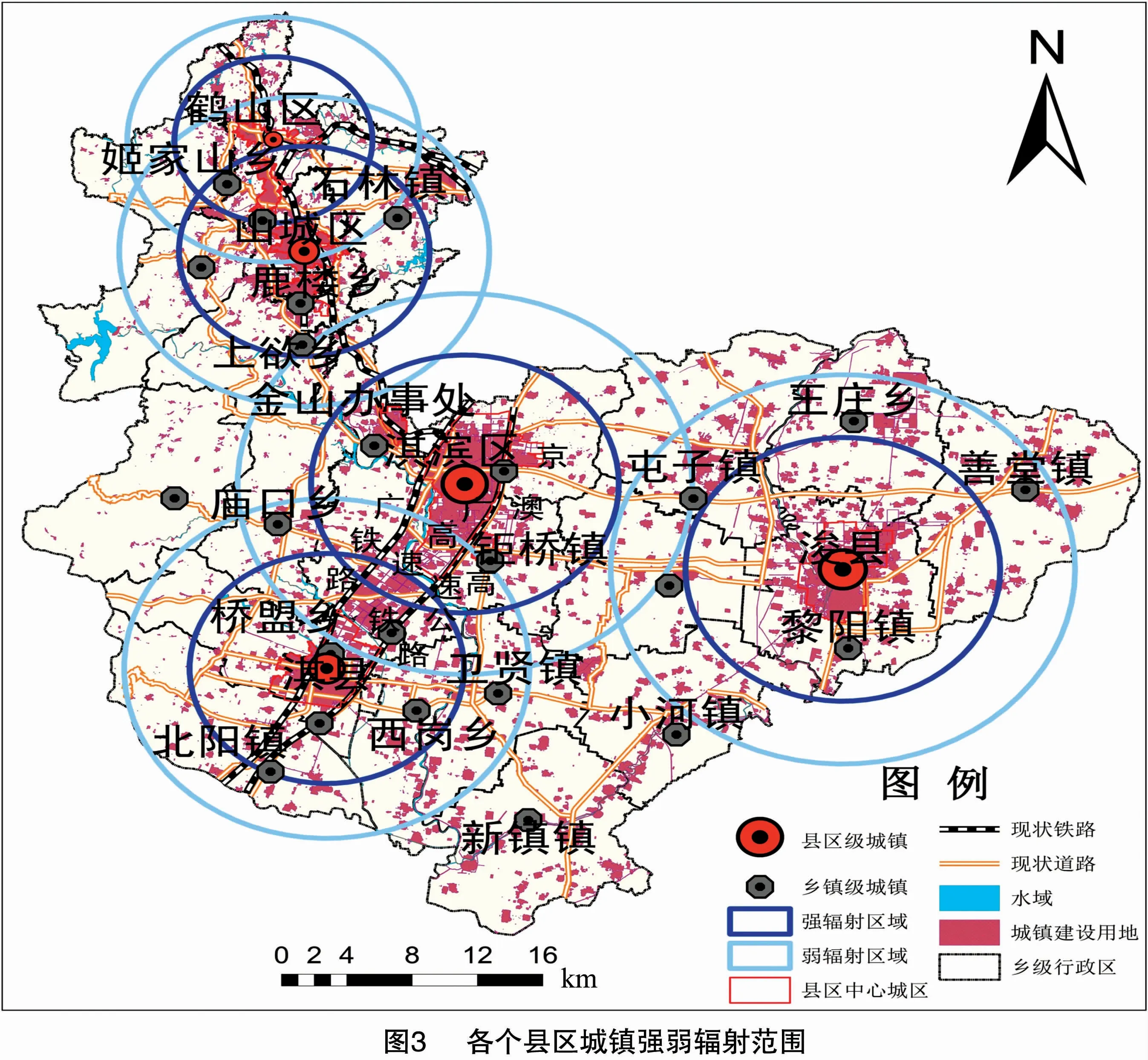
選擇淇濱區與淇縣之間的斷裂點處場強為邊界場強計算輻射范圍，主要原因：淇濱區與淇縣城市綜合規模指數均較大，并且相距較近，具有很大的輻射能量，從表4中也可以看出，2個城鎮斷裂點處場強明顯強于其他斷裂點處場強；淇濱區與淇縣位鶴壁市中部地帶，毗鄰多條交通干線，與周圍聯系密切，有利于對周圍城鎮產生帶動輻射作用。選擇各個斷裂點處場強平均值作為邊界場強計算弱輻射范圍，可以從整體上反映各個縣（區）中心城鎮對周圍小城鎮的影響范圍。輻射范圍計算見表5，依據輻射半徑繪制輻射范圍（圖3）。

4 結果與分析

由空間聚集計算結果可以看出，鶴山區、淇濱區、山城區、浚縣縣城、淇縣縣城的聚集維數D分別為0.992 1、1.238 7、0.989 4、1.180 2、0.948 2，相關系數r2分別為0.989 6、0.952 2、0.986 9、0.951 1、0.972 8。根據D的地理意義可得，鶴壁市縣（區）城鎮均具有優化的空間結構，表現出明顯的分形特征，城鎮體系的空間要素分布從中心城鎮向四周呈現密度遞減趨勢，其中以鶴山區、山城區、淇縣縣城為中心城鎮時，城市分布集中程度較高且聚集程度沒有顯著差異，當以淇濱區、浚縣為中心城鎮時，城市分布集中程度較低，且聚集程度明顯低于其他3個城鎮。從總體上看，鶴壁市城鎮體系空間結構仍處于不平衡發展的階段，筆者認為，一方面是由于地形地貌因素，鶴壁市地形西高東低呈現階梯式分布，鶴山區、山城區、淇縣均位于太行山東麓與華北平原接壤地帶，地勢相對不平坦，西部多山地制約著城鎮的發展，東部為廣袤的平原地帶，為城鎮建設提供了良好的地理條件，周圍小城鎮圍繞中心城鎮快速發展，呈現聚集態分布；另一方面是由于歷史發展原因，1957年鶴壁市市區建設選址在西北部鶴壁集鎮，即現在的鶴山區，1959年鶴壁市市區向南搬遷至山城區，由于鶴壁市前2次緣礦而建的城市發展理念，市區周圍基本都是煤炭開采造成的塌陷區，鶴壁市城市擴展受到嚴重制約。1999年鶴壁市城區遷到中部平原地帶，即現在的淇濱區，到現在僅經歷十幾年的發展，發展時間尚短，且淇濱區和浚縣位于中部和東部廣袤的華北平原地帶，周圍小城鎮大多以農業為主，城鎮之間相距較遠，分布較為分散，交通聯系還不夠密切，對周圍城鎮吸引能力還有待提升。

表2 鶴壁市兩兩城鎮間歐氏距離矩陣

表3 標度r及其對應的關聯函數N（r）

表4 淇濱區與各縣區城鎮之間的斷裂點及斷裂點處場強

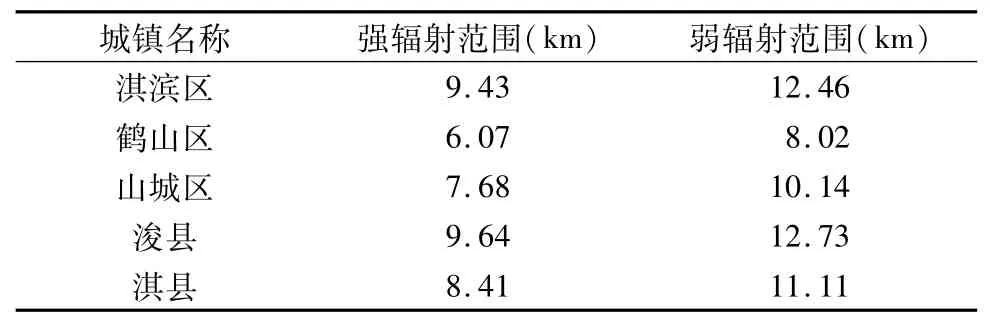
表5 各縣區城鎮強、弱輻射范圍

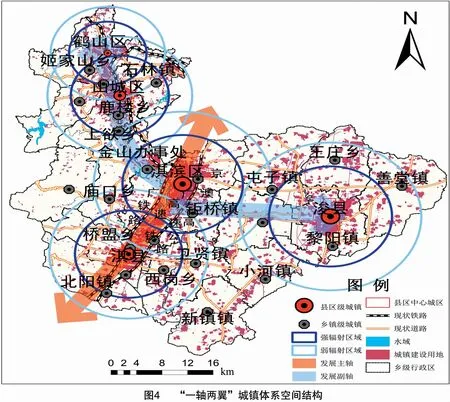
由關聯分析可以看出，鶴壁市城鎮體系空間結構的關聯維數D＝1.194 3。根據關聯維數的地理意義可知，鶴壁市城鎮體系空間相互作用還比較弱，城鎮之間相互聯系不緊密。從表2中可以得出，鶴壁市城鎮體系最近距離（每個城鎮與其最近城鎮的距離）的均值為5.34 km，其中西北部（鶴山區、山城區）最近距離均值為3.96 km，中南部（淇濱區、淇縣）最近距離均值為4.18 km，東部（浚縣）最近距離為8.07 km，中西部最近距離均值均小于整體均值，東部最近距離明顯大于整體均值，進一步說明地形地貌對鶴壁市城鎮體系空間分布的影響。D值接近于1，表明鶴壁市城鎮體系分布近似圍繞某條地理線集中分布，并呈現“一軸兩翼”的特征（圖4）。“一軸”即城市發展主軸沿重要交通干線分布，如淇濱區、淇縣均沿國道G107、京廣澳高速公路、京廣高速鐵路沿線分布，并逐漸呈現相互接壤融合趨勢。“兩翼”即老城區城鎮組團和浚縣城鎮組團，通過城市發展副軸實現主城區與“兩翼”的互通連接，帶動鶴壁市西北部和東部經濟的發展。

由圖3可以看出，在鶴山區、山城區、淇濱區、浚縣和淇縣輻射范圍內小城鎮數量分別為2、6、3、1、5個，雖然山城區輻射范圍比浚縣小，但由于地形地貌原因以及山城區作為歷史上鶴壁市中心城區，經歷了長時間的社會經濟發展，其影響輻射到的小城鎮數量要明顯比浚縣多，進一步說明地形地貌和歷史發展因素對城鎮體系空間分布的影響。鶴山區和山城區、淇濱區和淇縣輻射范圍均存在交匯處并逐漸交融，隨著城鎮邊界的擴展，最終將實現城鎮融合，“一軸兩翼”的城鎮體系空間格局將更加凸顯。

基于城鎮體系空間分形分析和中心城鎮輻射范圍識別，對鶴壁市城鎮體系空間結構優化提出以下建議：（1）增強城市發展主軸周圍城鎮集聚功能。依據點軸理論，應立足于淇濱區和淇縣地理位置優勢，加快推進2個中心城鎮接壤，壯大主城區城鎮規模，形成鶴淇核心經濟軸帶。并通過核心經濟軸帶的輻射，由線到面擴展其影響范圍，從而帶動周圍城鎮體系向核心經濟軸帶聚集，準確定位鶴淇核心經濟軸帶沿線城鎮產業結構，實現區域城鎮產業互補，避免城鎮間產業同構造成的競爭。（2）準確定位斷裂點處和輻射交匯處城鎮職能。立足于“一軸兩翼”的城鎮體系空間結構，在積極發展城市主軸，培育“兩翼”組團城鎮綜合經濟實力的同時，構建鶴壁市“多軸帶網絡型”城鎮體系空間結構（圖5），增強軸帶節點處重點城鎮的經濟實力，形成鶴壁市經濟增長極網絡式分布，逐步實現鶴壁市城鎮體系向高級穩定狀態過度，從而提升鶴壁市城鎮體系綜合實力。（3）加快鶴壁市內綜合交通網絡建設。沿城市發展軸線完善交通基礎設施，發揮城鎮體系沿交通干線集中分布的地理區位優勢，提升城市發展主軸同周邊各個小城鎮的聯系密切程度，引導資源在核心城鎮間合理配置。

5 結論與討論

本研究基于分形理論和場強模型，運用ArcGIS空間分析方法，測算了鶴壁市縣（區）中心城鎮聚集維數和鶴壁市城鎮體系的關聯維數，識別了縣（區）中心城鎮強、弱輻射范圍，結果表明：（1）縣區中心城鎮城鎮體系空間結構均具有明顯的分形特征，鶴山區、山城區、淇縣城鎮體系空間結構聚集程度相差不顯著，但均高于淇濱區和浚縣城鎮體系空間結構聚集程度，其原因可能是由于鶴壁市地形地貌因素和歷史發展原因共同導致。（2）鶴壁市城鎮體系整體關聯維數D ＝1.194 3，說明鶴壁市城鎮體系空間相互作用還比較弱，城鎮之間相互聯系不緊密，由于地形地貌原因，西部與中部城鎮間聯系相對緊密，東部地處廣袤平原地帶，城鎮間聯系相對不緊密；城鎮體系近似沿國道G107、京廣澳高速公路、京廣高速鐵路分布，其空間結構呈現“一軸兩翼”的分布特征。（3）在縣（區）中心城鎮輻射影響力方面，淇濱區和浚縣輻射范圍相差不明顯，但均明顯大于鶴山區、山城區和淇縣，由于地形地貌原因，其城市綜合規模還需提升，對周圍小城鎮的輻射影響力還需進一步增強。

城鎮體系是一個復雜開放的系統，其空間結構是動態演化的結果，是由其內部各個結構和外界其他系統共同作用形成的，本研究僅揭示了其城鎮體系空間結構的分布特征、聯系緊密程度及縣（區）中心城鎮輻射范圍，并對5個縣（區）進行了橫向對比分析。在方法上采用鶴壁市城鎮建設用邊界幾何中心，相比傳統以行政區為幾何中心進行測度，結果更符合實際情況，但在城鎮體系空間結構縱向歷史演變趨勢方面分析較少，對城鎮體系系統內部結構相互作用機理分析還不夠明確。