弧形閘門的模態(tài)特征及地震時程分析
李云龍,顧曉峰,胡友安
(1.河海大學(xué)機電工程學(xué)院,江蘇 常州 213022;2.江蘇省太湖水利規(guī)劃設(shè)計研究院有限公司,江蘇 蘇州 215128)
0 引言
閘門運行過程中會出現(xiàn)振動現(xiàn)象,當水流脈動和閘門產(chǎn)生共振或者在地震時,閘門結(jié)構(gòu)經(jīng)常會被強烈的震動破壞。例如,唐山地震對陡河、密云兩個水庫造成了嚴重破壞;汶川地震也造成了紫平鋪和沙牌壩的局部損壞[1]。為了將地震的損害降到最小,應(yīng)對地震敏感區(qū)的閘門進行嚴格的抗震分析,在進行地震分析之前應(yīng)該先通過模態(tài)計算了解閘門的振動特性。
經(jīng)查閱文獻發(fā)現(xiàn),以往的鋼閘門抗震計算基本都采用擬靜力法和反應(yīng)譜法,這2種方法仍屬于等效靜力法范圍[2],并未真正考慮地震持續(xù)時間對結(jié)構(gòu)內(nèi)力響應(yīng)的影響。對于弧形閘門等不規(guī)則結(jié)構(gòu),相關(guān)抗震規(guī)范多要求采用時程分析法進行補充計算。本文以某中型弧形閘門為研究對象,采用地震時程分析方法,在不考慮動水壓力和考慮動水壓力2種工況下,研究弧形閘門在地震波作用下的位移和應(yīng)力的時程響應(yīng),對計算結(jié)果進行比較分析,校核閘門的強度和剛度,并對弧形閘門的結(jié)構(gòu)設(shè)計給出相應(yīng)的修改意見。
1 弧形閘門有限元模型及材料參數(shù)
以某溢洪道弧形閘門為設(shè)計研究對象。設(shè)計水頭為8 m,閘門底檻高程22.1 m,孔口寬11 m,閘門面板半徑為11 m,寬10.8 m,板厚0.01 m,面板上分布有2根主梁、4根豎直梁和2根邊梁。面板、主梁、豎直梁等均采用Shell63單元模擬,頂梁、橫梁等采用Beam188單元模擬,鉸支座采用Solid185單元模擬。弧形閘門的有限元模型如圖1所示,坐標系采用圓柱坐標系,X軸為閘門徑向,Y軸為切角θ,Z軸為鉸支座軸向。

圖1 弧形閘門有限元模型Fig.1 Finite element model of arc gate
閘門全閉時的約束形式:鉸支座軸孔內(nèi)表面上的節(jié)點約束X向和Z向自由度,釋放Y向的轉(zhuǎn)動自由度;閘門側(cè)止水約束Z向自由度;底止水處約束Y向的轉(zhuǎn)動自由度。
閘門的材料為Q345鋼,彈性模量E=201 GPa,泊松比ν=0.3,密度ρ=7 850 kg/m3;止水的材料為橡膠,考慮到地震時程分析用時較長,將橡膠按照線性材料處理,其彈性模量E=6.1×10-3GPa,泊松比 ν=0.493,密度 ρ=1 000 kg/m3。
閘門整體鋼板厚度小于16 mm,根據(jù)SL 74—2013《水利水電工程鋼閘門設(shè)計規(guī)范》規(guī)定,屬于容許應(yīng)力尺寸分組第1組,對應(yīng)的容許應(yīng)力為[σ]=225 MPa。由于此弧形閘門屬于中型工作閘門,容許應(yīng)力需取調(diào)整系數(shù),此處取0.95,故閘門的容許應(yīng)力為[σ]=213.8 MPa。露頂式工作閘門的主梁最大撓度與計算跨度之比不得超過1/600,次梁最大撓度與計算跨度之比不得超過1/250,經(jīng)計算,主梁最大撓度為16.67 mm,次梁最大撓度為40 mm。
2 弧形閘門模態(tài)分析
2.1 附加質(zhì)量的模擬
假設(shè)水體為不可壓縮性流體時,水體的動力作用可以簡化為在模型的質(zhì)量矩陣中加上1個附加質(zhì)量矩陣[3]。本文流體和固體交界面上節(jié)點所施加的附加質(zhì)量根據(jù)Westergaard公式施加[4]。對于面板上殼單元節(jié)點i,作用其上的單位面積動水壓力為:


式中:Ai為與節(jié)點i相關(guān)的面積。在ANSYS中采用三維Mass21單元模擬交界面節(jié)點的附加質(zhì)量,由于動水壓力方向垂直于面板,故在分析時只需定義動水壓力方向上的質(zhì)量即可[5]。
2.2 弧形閘門振動特性研究
分析弧形閘門關(guān)閉時,在不同水頭下的自振頻率,研究水體對閘門自振頻率的影響。查閱相關(guān)文獻可知,水流脈動頻率主要集中在1~20 Hz,優(yōu)勢區(qū)在0~4 Hz[6],弧形閘門高階自振頻率遠離水流的脈動頻率區(qū),對弧形閘門整體結(jié)構(gòu)的安全不會造成很大威脅,所以本文主要研究弧形閘門前十階自振頻率。圖2為8 m水頭下閘門的第一階振型,表1所示為不同水頭下弧形閘門的振動頻率。

圖2 8 m水頭下閘門第一階振型Fig.2 1st mode shapes of gate under 8 m water head
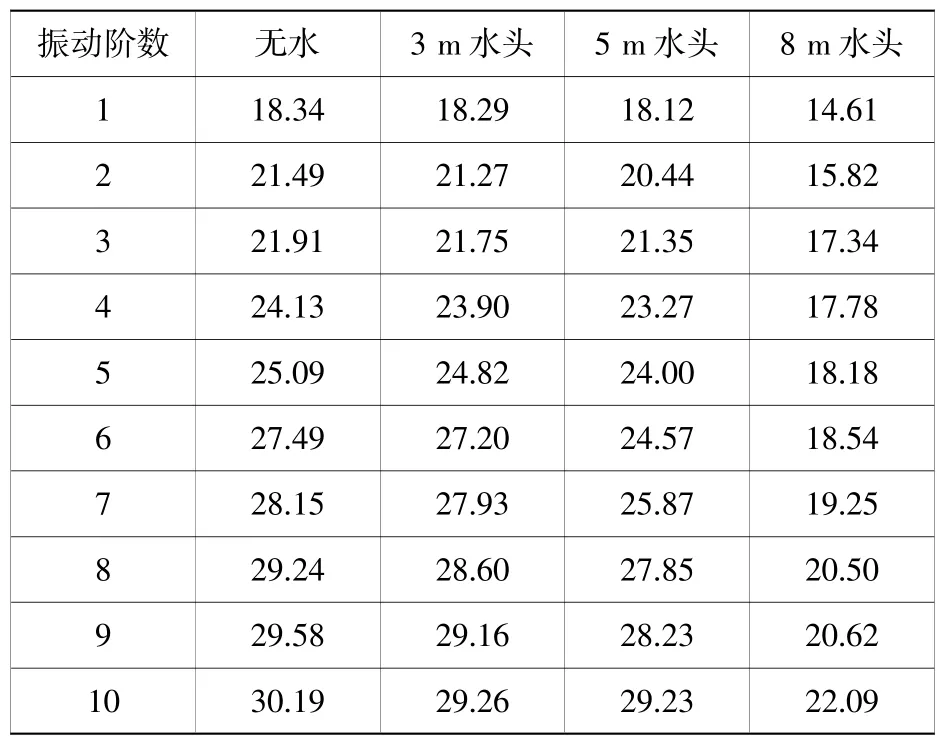
表1 不同水頭下弧形閘門的振動頻率Table 1 Vibration frequencies of arc door under different water heads Hz
由表1可知,隨著水頭的增加,閘門的自振頻率有所降低,這是由于隨著水頭的增加,附加質(zhì)量增大,流固耦合效應(yīng)更加明顯。進一步查看不同水頭下振型,由于側(cè)止水剛度較低,無水、3 m水頭和5 m水頭情況下閘門第一階振型均呈現(xiàn)整體振動趨勢,8 m水頭時閘門主要表現(xiàn)為面板頂部的法向振動。可見隨著水頭的增加,閘門的自振頻率和振型均發(fā)生變化,所以在進行動力分析時,需要考慮動水壓力。
3 弧形閘門地震時程分析
3.1 地震時程分析法及地震波選取
地震時程分析法原理:根據(jù)選定的地震波和結(jié)構(gòu)恢復(fù)力特征曲線,采用逐步積分法直接積分動力方程,從而得到在地震過程中每個時刻結(jié)構(gòu)的變形和應(yīng)力[7]。地震時程分析可以觀察結(jié)構(gòu)在地震載荷作用下從變形到斷裂破壞的全過程。在地震時程分析中,地震波以加速度時程形式表示。根據(jù)有限單元法原理將結(jié)構(gòu)進行離散化之后,依據(jù)D "Alembert原理就可以得到結(jié)構(gòu)體系的運動方程為[8]:
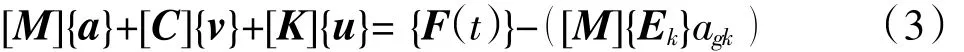
式中:[M]、[C]、[K]為結(jié)構(gòu)的質(zhì)量矩陣、阻尼矩陣和剛度矩陣;{a}、{v}、{u}為結(jié)構(gòu)相對于地面的相對位移矩陣、相對速度矩陣和相對加速度矩陣;{F(t)}為荷載矩陣;agk為地震加速度(k=x、y、z);{Ek}為地面運動影響系數(shù)矩陣。
本文阻尼采用瑞利阻尼[9],公式如下:

式中:M為結(jié)構(gòu)的質(zhì)量矩陣;K為結(jié)構(gòu)的剛度矩陣;ξ為結(jié)構(gòu)阻尼比,此處取為0.05;fi、fj為結(jié)構(gòu)第i、j階自振頻率,本文取i=1、j=2。地震加速度采用對應(yīng)溢洪道弧形閘門相關(guān)文件所提供的地震加速度數(shù)據(jù)。圖3為加速度時程曲線。

圖3 加速度時程曲線Fig.3 Acceleration time history curve
3.2 地震時程分析
本文主要研究閘門全閉時,在8 m設(shè)計水頭作用下,2種不同工況下閘門的應(yīng)力時程響應(yīng)和位移時程響應(yīng)。首先對8 m設(shè)計水頭作用下的閘門進行靜力分析,然后以靜力分析結(jié)果作為初始狀態(tài)施加動水壓力和地震加速度進行地震時程分析。在地震過程中,靜水壓力和重力保持不變;動水壓力采用附加質(zhì)量進行模擬,質(zhì)量點質(zhì)量大小根據(jù)公式(2)計算,隨著地震加速度的改變,附加質(zhì)量產(chǎn)生的慣性力也隨之改變,從而模擬動水壓力;地震加速度施加在閘門約束處,包括支鉸、側(cè)止水及底止水處。表2為分析工況表。圖4為地震工況一和地震工況二下,閘門最大的Von Mises應(yīng)力和最大總位移時程曲線;圖5為地震工況二下,閘門應(yīng)力最大時刻9.32 s時的應(yīng)力分布云圖。

表2 工況表Table 2 Working condition table
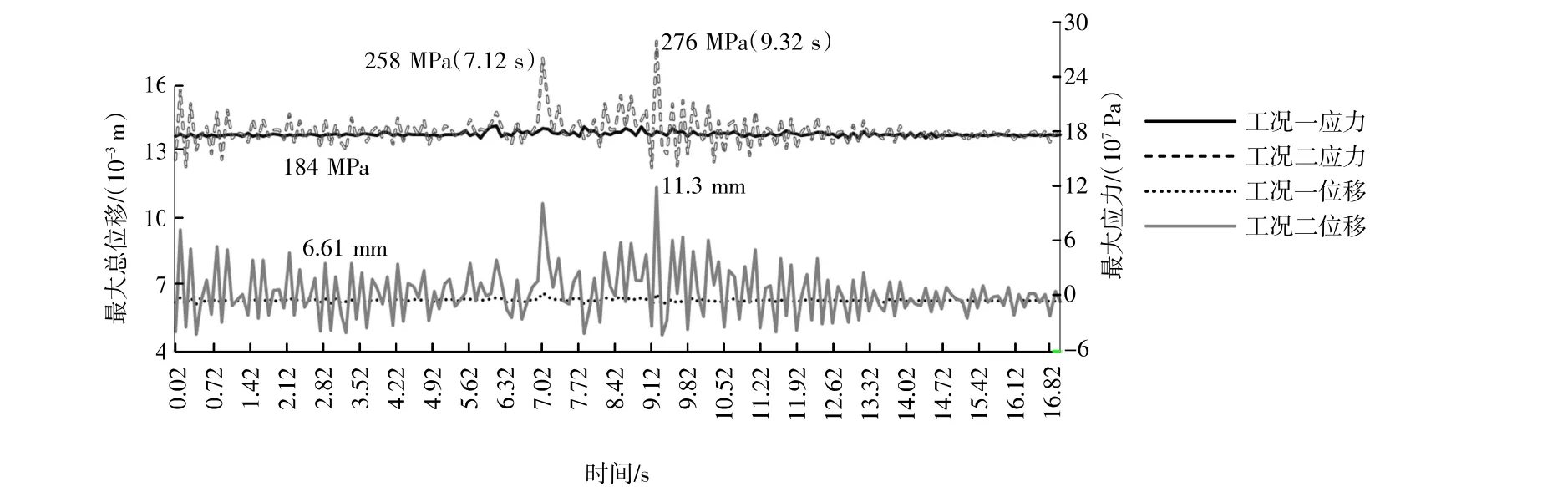
圖4 最大Von Mises應(yīng)力和最大位移時程曲線Fig.4 Time History Curve of maximum Von Mises stress and maximum displacement

圖5 9.32 s時閘門應(yīng)力云圖Fig.5 Stress nephogram of gate at 9.32 s
靜力工況下,閘門最大應(yīng)力為171 MPa,最大位移為5.91 mm,滿足強度和剛度要求。
從圖4中可以看出,地震過程中,在不考慮動水壓力的情況下,閘門最大應(yīng)力為184 MPa,閘門整體的最大位移為6.61 mm,比靜力工況稍微有所增加,但均未超過許用值,閘門結(jié)構(gòu)在地震工況一下滿足強度和剛度要求。
在考慮動水壓力的情況下,閘門在地震過程中的最大應(yīng)力時刻為9.32 s,最大應(yīng)力為276 MPa,次高應(yīng)力時刻為7.12 s,次高應(yīng)力為258 MPa,均超出了容許應(yīng)力,閘門整體最大位移為11.3 mm,小于許用撓度。地震工況二下閘門的應(yīng)力和位移變形均明顯增加。從圖5中可以看到,9.32 s對應(yīng)的最大應(yīng)力發(fā)生在支臂和底梁連接處,其次支臂腹桿和豎直梁的連接處應(yīng)力也較大,其形式均為局部應(yīng)力集中;同樣的在7.12 s時,在同樣的位置也存在局部應(yīng)力集中。
3.3 閘門結(jié)構(gòu)優(yōu)化及地震工況校核
為了緩解支臂及支臂腹桿連接處的應(yīng)力集中問題,分別在支臂腹桿與豎直梁連接處及閘門底部增設(shè)了厚度為10 mm的肋板,具體模型見圖6,圖中黑色加深區(qū)域為增設(shè)的肋板;對優(yōu)化后的閘門進行表2中地震工況二下的地震時程分析。圖7為閘門優(yōu)化后應(yīng)力最大時刻9.32 s對應(yīng)的閘門鋼結(jié)構(gòu)應(yīng)力云圖。

圖6 閘門優(yōu)化后的模型Fig.6 Optimized model of gate

圖7 閘門優(yōu)化后9.32 s時閘門應(yīng)力云圖Fig.7 Stress nephogram of gate at 9.32 s after gate optimization
閘門結(jié)構(gòu)優(yōu)化后在地震過程中閘門最大應(yīng)力為194 MPa,最大位移為7.53 mm,均在許用范圍內(nèi),因此在8 m設(shè)計水頭下優(yōu)化后的閘門滿足地震工況的強度和剛度要求。從圖7中可以看出在增加肋板之后,閘門支臂和梁格連接處的應(yīng)力集中得到明顯改善,結(jié)構(gòu)優(yōu)化效果明顯。
4 結(jié)語
1)通過研究分析不同水頭下的閘門模態(tài)結(jié)果,可以發(fā)現(xiàn)水體可以降低閘門的自振頻率,并改變閘門的振型,因此在動力分析時應(yīng)考慮水體的影響。
2)通過比較兩種不同地震工況下閘門的地震時程響應(yīng),發(fā)現(xiàn)考慮動水壓力的情況下,地震過程中閘門的應(yīng)力和變形顯著增加。可見在地震過程中動水壓力對閘門的變形起到很大影響,地震動水壓力不可忽略。
3)在地震工況二下,閘門在地震過程中出現(xiàn)了局部應(yīng)力集中現(xiàn)象,最大應(yīng)力超出了容許應(yīng)力,不滿足強度要求。分別在支臂腹桿與豎直梁連接處及閘門底部增設(shè)肋板后,應(yīng)力集中得到明顯改善,優(yōu)化后的閘門可以在地震工況下安全運行。本文研究方法可為同類閘門的強度、剛度校核及結(jié)構(gòu)優(yōu)化提供參考依據(jù)。

