立足生本 自然生長 提升素養
——“位置的確定”教學設計及反思

■馬 敏

（作者單位：江蘇省連云港市教育局教研室）

【學習目標】

通過游戲活動，感悟生活中描述物體位置的重要性和必要性；通過豐富的現實情境和數學情境，感受確定位置的方法，感受數量變化和位置變化的聯系，發展數形結合意識、形象思維能力和數學應用能力。

【學習重、難點】

重點：掌握并運用坐標法、方向角加距離法確定物體位置；了解運用經緯法、區域定位法確定物體位置。

難點：把實際問題轉化為數學問題——數學建模意識的培養；體悟數量變化與位置變化的聯系——數形結合意識的培養。

【設計思路】

運用自主、合作探究、實驗的教學模式，學生通過對生活中和數學中確定位置不同方法的探究，經歷數學的抽象過程，感悟數學的應用價值，體驗成功的喜悅和合作的快樂。課前讓學生自己去查找經緯線、區域定位等資料，參與到課堂的全過程。整節課設計以“開放、合作、探究”為主線，給學生充分的思考的空間和表現的機會，讓學生在一個較為寬松的氛圍中去體驗數學學習帶來的樂趣。

【教學流程】

活動一：對號入座

師：歡迎同學們走進今天的課堂，不過你得先拿著課前老師發給你的座位號卡，找到你的座位。

（注：此處25張座位號卡，其中設計3個特殊的座位號，一個是只寫有數字3，另外兩張分別寫有4，5和5，4，其余學生的座位號寫明“第×行，第×列”或“第×列，第×行”。）

問題1.問手持數字“3”卡的學生：你怎么一直在教室里徘徊？直到最后你才猶豫地坐在了這個位置上？

生：我的卡片與其他同學的不一樣，只有1個數字3，我不知道是第3行還是第3列，更不知道是哪個位置，最后看到就剩這個位置，它正好在第3行（列）上，所以我才坐下的。

師：原來只有1個數字的座位號讓你無法確定自己的位置。你能告訴同學們你現在所坐的座位號應該是什么嗎？

問題2.問手持“4，5”和“5，4”卡的學生：你們怎么站在了同一個位置上？

生1：我們的卡上都寫著數字4和5，但我認為我的是第4列第5行，而他的應該是第5列第4行，所以這個位置應該是我的。

生2：我認為他說的不對，其他同學的都明確是第×行第×列，而我們的上面只有2個數字，那么它們一定是1個是行數，1個是列數，所以我認為我的也可以是第4列第5行。

師：你們卡上的數字順序不同，讓你們產生了不同的理解，一個同學認為第1個數是列數，第2個數是行數，而另一個同學則相反。

問題3.假如我們約定“列數在前，行數在后”，那這個位置應該屬于誰呢？如果老師再提供一個位置，應該放在哪兒呢？

（設計意圖：從學生的生活經驗出發，創設情境，提出問題，激發學生學習數學的興趣。讓學生通過親身經歷從具體情境中發現數學問題，進而解決問題的全過程，感受現實世界中蘊含的大量的數學信息。）

問題4.怎樣才能準確確定教室里座位的位置？行數和列數的先后順序對位置有影響嗎？如果老師用（3，2）表示第3行第2列的同學座位號，那么你的座位號應該如何表示呢？

問題5.生活中還有類似這樣確定物體位置的實例嗎？

（設計意圖：圍繞確定教室中學生的座位這個問題進行討論，讓學生體會確定位置時需要兩個數據，并且感受到這兩個數據的順序的重要性，同時為學生后續學習平面直角坐標系奠定基礎。最后1個問題具有開放性，根據學生的回答可能涉及3個數據確定位置的方法，教師適時加以說明。）

活動二：經緯法表示位置

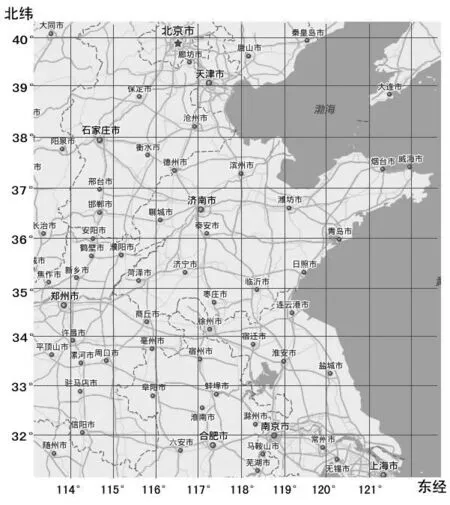
問題1.老師繪制了一張平面化的經緯圖，請你說說連云港市的地理位置。利用這張圖，你還能說說濟南的位置嗎？

問題2.如果告訴你一組經度和緯度，你能說出是哪個城市嗎？

問題3.每年的夏秋季是臺風的多發時期，沿海城市的人們都會比較關注每一次臺風的運動過程是否會對自己的城市造成影響，請根據表中數據，繪制一張經緯網圖，并用平滑的曲線表示臺風中心移動路徑。

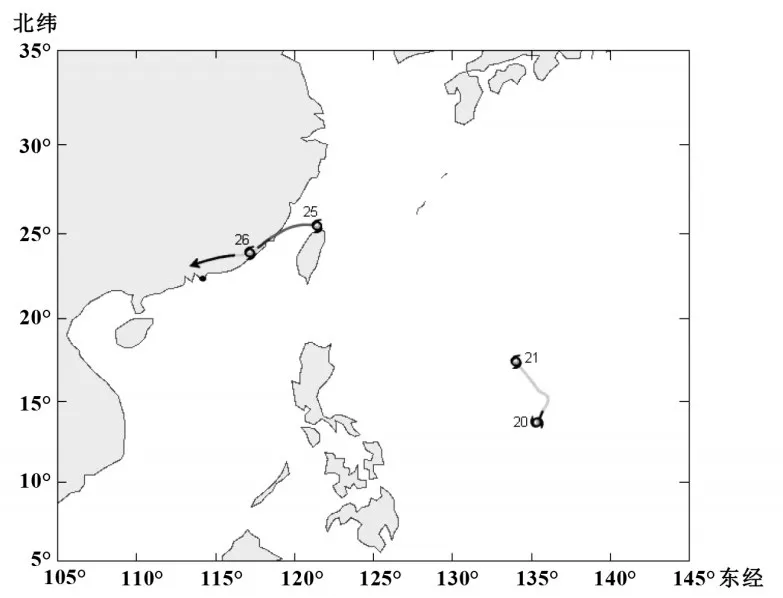
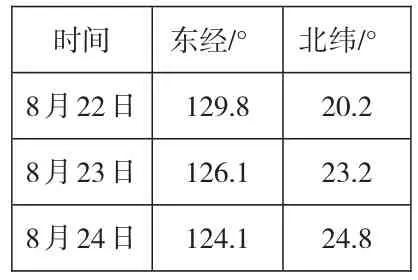
時間8月22日8月23日8月24日東經/°129.8 126.1 124.1北緯/°20.2 23.2 24.8

（設計意圖：學生經歷運用所學知識尋找實際背景的過程，在自主探究中熟悉了確定位置的第二種方法：經緯法。同時讓學生體悟由點找坐標以及由坐標確定點的方法。）

活動三：區域定位法

問題1.如果你的一位外地朋友來我們美麗的靖江，為了你的朋友查找景點方便，你可以仿照經緯網將我市的主要旅游景點劃分成區域。你如何介紹馬洲公園所在的區域？在這一區域還有哪些景點呢？

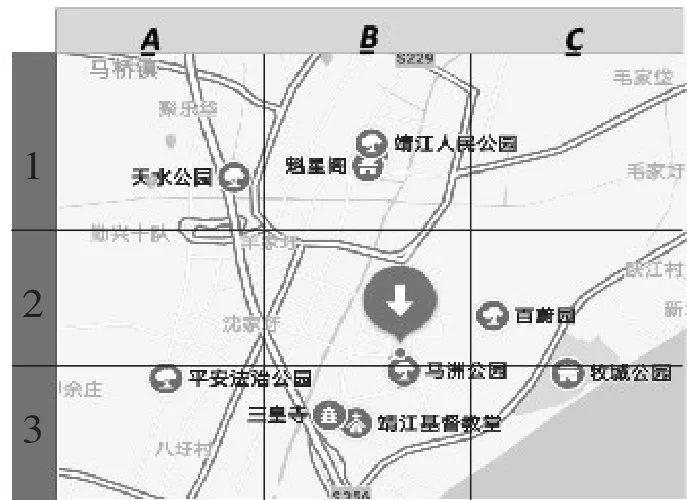
問題2.生活中有類似確定物體位置的例子嗎？

（設計意圖：問題1暗含區域定位法；學生看到問題2，根據經驗都會想到大型演出或者活動等，也是先分區域再定位置，實質就是利用區域定位和有序數對確定物體位置。）

活動四：利用方向角和距離定位

問題1.你的朋友在參觀完梅蘭芳紀念館之后，準備到另一著名景點——城隍廟去看看。如果現在只知道城隍廟在梅蘭芳紀念館的北偏西55°方向，你能確定它的位置嗎？

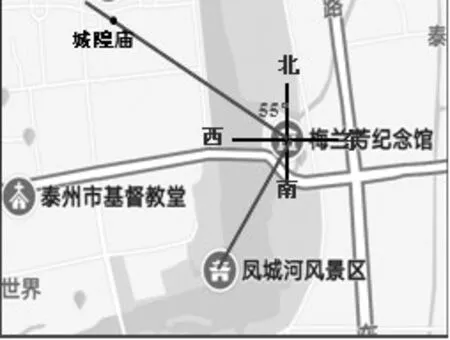
問題2.如果老師再告訴你梅蘭芳紀念館與城隍廟之間的圖上距離為5cm。請你利用上圖，找到城隍廟的位置。

問題3.請用同樣的方法，描述一下鳳城河風景區相對于梅蘭芳紀念館的位置（畫圖并測量），并請同學們思考梅蘭芳紀念館相對于鳳城河風景區的位置。

（設計意圖：此種確定位置的方法是本節課的難點，學生需要在教師的指導下自主操作完成。首先要找到觀測點、建立方向標，然后測量目標與觀測點之間的距離，從而找到用“方向角+距離”確定物體位置的方法。）

活動五：實踐應用

問題1.根據下列提示，繪制一張老師的家鄉連云港的市區主要風景區示意圖。

（1）學校位于（1，2）；

（2）花果山鄉的位置為（4，5）；

（3）花果山風景區在花果山鄉的正東面4km；

（4）云龍澗風景區位于（9，6）；

（5）東磊風景區在花果山風景區的南偏東45°方向，同時在云龍澗風景區南偏西45°方向；

（6）從云龍澗風景區向右走4格，再向上走5格到達新亞歐大陸橋東端起點。

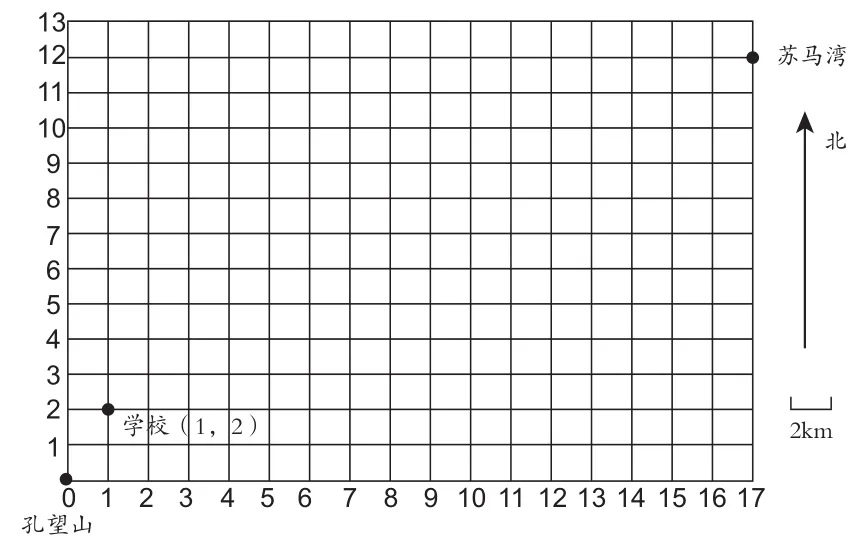
問題2.在你所繪的圖上，蘇馬灣和孔望山的位置如何表示？

（設計意圖：設置此應用問題，讓學生綜合運用“坐標法”和“兩條射線交點法”這兩種確定物體位置的重要方法，旨在突出重點，突破難點，提高學生綜合運用知識的能力。）

活動六：數學中位置的確定

問題1.l是線段BC的垂直平分線，在點A沿直線l自上而下運動的過程中，圖中的一些線段的長短、角的大小也隨之變化。

（1）∠BAC的大小是如何變化的？

（2）點A在什么位置時，△ABC是等邊三角形？是直角三角形？

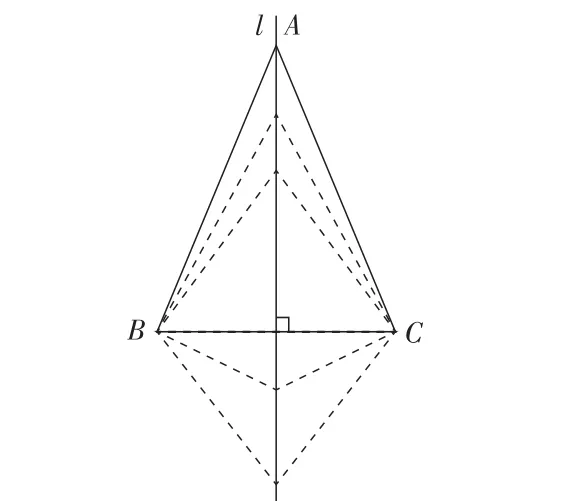
（設計意圖：先操作觀察。再結合教師的幾何畫板演示，引導學生關注數量變化與位置變化關系在數學中的體現。同時在此基礎上，引導學生自己提出問題，以增強學生“發現問題和提出問題”“分析問題和解決問題”的能力。）

活動七：反思感悟

問題1.確定平面內物體的位置有哪些常見的方法？每種方法需要幾個數據？生活中如此，數學中呢？說說你的看法。

問題2.這節課我們共同探討了在平面內確定物體位置的幾種方法，它們一般需要兩個數據，可以是一對有序數對，可以是方向角和距離，還可以用兩條線的交點，或通過區域來確定物體的位置。在我們生活的空間中的物體的位置是否也可以用數字確定？希望同學們課后可以利用今天所學的知識找到答案。

問題3.如果在剛才的連云港的景區示意圖中，向左走3格，再向下走6格，到達東海溫泉，請問東海溫泉的位置如何表示呢？

（設計意圖：三個問題層層深入，問題1是回顧，回憶確定平面內物體位置的方法，感悟數量變化與位置變化的關系。問題2是從二維位置確定到三維位置確定，讓思維升華。問題3是讓學生在思維沖突中促進思考，為下一節課平面直角坐標系做好鋪墊。這樣的有層次的問題會讓學生的學習從課內向課外延伸，讓學習不再是片段化的知識點，而是整體建構下的生長的學、有需要的學。）

教學反思：

作為本章的第一節，本節課承載著平面直角坐標系的鋪墊功能。5個“動手做數學”的活動：對號入座→查找地圖→景點分區→測量定位→繪制旅游圖。以確定連云港市的主要旅游景點的位置為“主線”，以找座位、測量、繪制旅游圖等“動手做數學”活動為“路徑”，引導學生對生活中確定物體位置的不同方法進行探究，讓學生經歷數學的抽象過程（即數學化的過程），幫助學生感悟數學的應用價值，構建充滿生機的活力課堂。

本節課抓住學生已有的經驗，“對號入座”是基于學生看電影的經驗，表示城市的地理位置基于學生閱讀地圖的經驗，確定兩個景區相對位置基于學生測量的經驗，繪制景區示意圖基于學生獲取信息的經驗等。這些細微的經驗是學生每天都觸及和不斷累積的，因此，這節課中的“做數學”對學生而言是力所能及的。而當這些點滴經驗經歷“數學化”的過程之后，就變為方法經驗（確定物體位置的方法）。

在本節內容中，所承載的主要核心素養為直觀想象、數學抽象。如從學生的現實世界出發，通過尋找座位、確定城市地理位置、描出臺風中心位置的移動路徑、兩個景區的相對位置、繪制主要景區示意圖等活動，幫助學生數學地理解確定物體位置的不同方法。在這些活動的背后，其實都在做同一件事，也就是反復幫助學生進行“抽象”，讓學生經歷數學化的過程。比如說，“對號入座”可以幫助學生抽象出“行與列兩條線的交點”，從而確定一個同學的座位；“城市地理位置”查找幫助學生抽象“經線和緯線的交點”，從而確定一個城市（這里的城市也抽象成一個點）的位置；“兩個景區相對位置”的確定可以幫助學生抽象出“方向角的射線和距離確定的點”，從而可以確定相對位置；繪制市區主要風景區示意圖，則更是數學化的過程，其實就是平面直角坐標系的“雛形”。應該說，經上述的抽象過程，后續的平面直角坐標系的學習則是水到渠成之事了。