一種基于RBF神經網絡的雷達穩定轉臺復合控制方法
游新望,曹正才
(中國船舶重工集團公司第七二四研究所,南京211153)
0 引 言
艦載雷達常用的兩軸穩定系統一般采用基于坐標變換的電子平臺技術在方位和俯仰軸上分別對艦船搖擺姿態角(橫搖角、縱搖角和航向角)進行實時角度補償,方位軸完成扇掃、環掃、定位、跟蹤等控制功能,俯仰軸確保雷達波束指向保持與大地水平。方位和俯仰閉環控制對象受艦船姿態角影響呈現出明顯的非線性和時變不確定性,其速度和加速度皆隨艦船姿態角變化而變化,且方位轉速越快變化越劇烈[1]。為保證控制精度及控制系統的平穩性,PID控制參數必須根據天線轉速及艦船姿態角的變化而實時調整。當天線方位轉速范圍較寬且艦船姿態角變化劇烈時,PID參數整定難于取得較為理想的控制效果[2]。
PID控制算法由于其結構簡單、運算量小、物理意義明確等特點得到了廣泛應用。但是,對于那些難以精確取得數學模型的系統,PID控制的參數調整大多是憑經驗先比例調節,再積分調節,最后加微分,根據系統的調試效果不斷地尋找最合適的數值,反復湊試尋找最優。RBF神經網絡是性能優良的前向神經網絡,計算量小、學習速度快,在系統辨識和參數估計等有著廣泛應用。本文將RBF神經網絡與PID控制結合,同時采用前饋或順饋構成基于神經網絡PID的復合控制。實際應用表明,本方法既可保證系統的控制品質,又無需對PID參數進行細分整定,具有較強的實用性[3]。
1 RBF理論及其模型結構
徑向基函數(RBF?Radial Basis Function) 是 J.Moody和C.Darken于20世紀80年代提出的一種神經網絡。它是具有單隱層的3層前饋網絡,模擬了人腦中局部調整、相互覆蓋接收域的神經網絡結構,能以任意精度逼近任意連續函數,輸入到輸出的映射是非線性的,隱含層到輸出的映射是線性的,從而加快了學習速度并避免局部極小問題。RBF神經網絡結構如圖1所示。
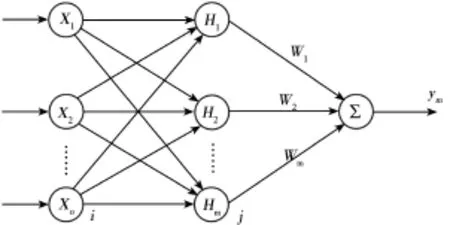
圖1 RBF網絡模型結構圖
在 RBF 網絡結構中,X=[x1,x2,…,xn]T為網絡的輸入向量。設RBF網絡的徑向向量H=[h1,h2,…,hj…,hm]T,其中hj為高斯基函數:

網絡的第j個節點的中心矢量為Cj=[cj1,cj2,…,cji,…,cjn]T,其中,i=1,2,…,n。
設網絡的基寬向量為B=[b1,b2,…,bm]T,bj為節點j的寬度參數,而且為大于零的數。網絡的權向量為W=[w1,w2,…,wj,…,wm]T,辨識網絡的輸出為
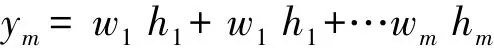
2 RBF網絡PID整定
RBF神經網絡PID控制結構圖如圖2所示。控制誤差為

增量式PID控制算法為

整定指標為

圖2 RBF網絡整定PID控制框圖

式中,kp,ki,kd的調整采用梯度下降法。

式中,?y/?u可通過神經網絡的辨識獲得。
3 基于RBF網絡的雷達穩定轉臺復合控制
本文以艦載雷達常用的方位和俯仰兩軸穩定轉臺作為被控對象,采用基于RBF網絡的復合控制,其中方位控制如圖3所示,俯仰控制如圖4所示。主閉環控制系統采用基于RBF網絡的PID控制器實現反饋控制,其控制參數通過RBF網絡的學習功能在線自動整定;采用前饋或順饋補償算法進一步降低控制誤差,確保控制精度滿足要求。
方位和俯仰轉臺控制采用基于坐標變換的電子平臺技術在雷達天線方位和俯仰軸上分別對艦船搖擺姿態角(橫搖角、縱搖角和航向角)進行實時角度補償,從而克服艦船搖擺對雷達系統的不利影響,確保天線軸線的指向精度。其中方位角A和俯仰角E的坐標變換公式如下[4]:

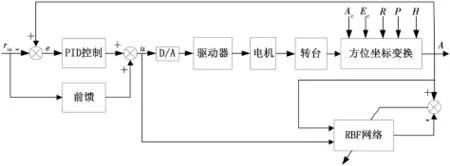
圖3 基于RBF網絡方位轉臺復合控制

圖4 基于RBF網絡俯仰轉臺復合控制
式中,P為甲板平面縱搖角,艦船艏艉線(縱軸)與水平面的夾角,艦艏在水平面上方為正;R為甲板平面橫搖角,甲板平面繞艦船艏艉線旋轉的角度,右弦下傾為正;H為航向角,從正北開始順時針到本艦艏方向的夾角,順時針為正;A為雷達波束方位角,正北與雷達波束指向在水平面投影線的夾角,順時針為正;E為雷達波束俯仰角,雷達波束指向與其在水平面投影線的夾角,夾角在水平面之上為正;Ac為雷達波束甲板平面方位弦角,艦艏線與雷達波束指向在甲板平面投影線的夾角,順時針為正;Ec為雷達波束甲板平面俯仰角,雷達波束指向與其在甲板平面投影線的夾角,夾角在甲板平面之上為正。
3.1 方位控制
以某雷達穩定轉臺為被控對象,艦船搖擺運動條件:橫搖±20°、周期 10 s;縱搖±5°、周期 5 s。 以轉速30°/s為例,雷達方位控制精度要求均方根誤差不大于0.3°。采用基于RBF神經網絡的復合控制方法,其閉環控制方位曲線及控制誤差如圖5所示,PID控制參數Kp、Ki及Kd變化曲線如圖6所示。從圖5、圖6可以看出,PID控制參數隨艦船搖擺變化實時調整,方位運動平穩且控制誤差較小。經計算得出方位控制誤差為 0.212°,滿足控制精度要求。

圖5 方位曲線及控制誤差
3.2 俯仰控制
以某雷達穩定轉臺為被控對象,艦船搖擺運動條件:橫搖±20 °、周期 10 s;縱搖±5 °、周期 5 s。 以轉速30°/s為例,雷達俯仰控制精度要求均方根誤差不大于0.55°。采用基于RBF神經網絡的復合控制方法,其閉環控制曲線及控制誤差如圖7所示,PID控制參數Kp、Ki及Kd變化曲線如圖8所示。從圖7、圖8可以看出,俯仰控制非線性特征明顯,其速度和加速度皆隨艦船姿態角及方位指向變化而變化,采用基于RBF神經網絡PID控制,PID控制參數隨艦船搖擺及方位指向變化而實時調整,俯仰運動平穩且誤差控制在合理范圍之內。經計算得出俯仰控制誤差為0.424°,滿足控制精度要求。

圖6 方位控制PID控制參數Kp、Ki及Kd變化曲線

圖7 俯仰曲線及控制誤差
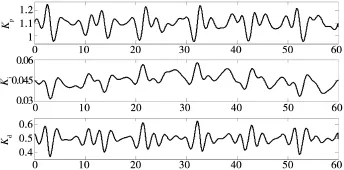
圖8 俯仰控制PID控制參數Kp、Ki及Kd變化曲線
4 結束語
從以上的方位、俯仰控制誤差曲線可以看出,該控制誤差滿足某兩軸穩定雷達轉臺閉環控制誤差精度要求,并且PID控制參數Kp、Ki及Kd變化曲線隨著艦船姿態角變化實時的在線整定,避免了在不同轉速及不同海況條件下對PID控制參數進行人工細分整定,具有較強的實用性。
綜上所述,利用RBF神經網絡在線學習功能,本文采用的基于RBF神經網絡PID復合控制方法,實現對控制參數進行在線整定功能,能達到理想的穩定誤差穩定精度要求,驗證了其應用于兩軸穩定雷達轉臺控制的可行性。

