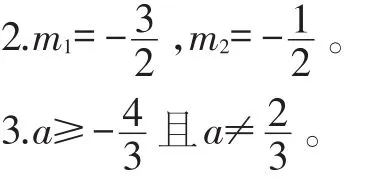“分 式 方 程”中典型錯解舉例分析
李 青

分式方程是初中階段重要的知識點之一,它是整式方程的拓展與延伸,但是分式方程的相關運算與整式方程相比較,運算步驟繁復,解題方法靈活多樣,在學習和運用的過程中更容易出錯。下面就分式方程中易混、易錯的地方加以舉例剖析,希望對同學們的學習能夠有所幫助。
一、對分式方程的概念理解不透
例1下列各式是分式方程的是 。
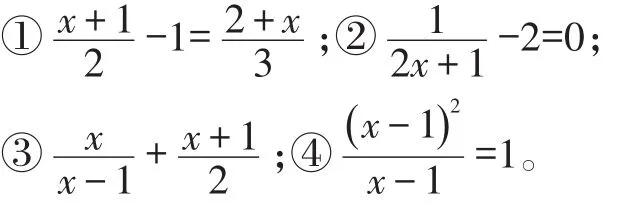
【錯解】②③。
【剖析】這一題出現錯誤主要是因為對分式方程的概念理解不透。分式方程要滿足兩個條件:(1)必須是一個方程;(2)分母中要含有未知數。而③式只是一個代數式,并不是一個方程,所以③不是分式方程;對于1,由于約分后的結果是一個整式方程,所以許多同學認為它不是分式方程,其實判斷一個方程是不是分式方程,一定要看它約分前的特征,所以④是分式方程。
【正解】②④。
二、解分式方程時,忘記驗根
例2解方程:
【錯解】方程兩邊同乘(x+2)(x-2),得(x-2)2-(x+2)2=16。解這個方程,得x=-2。所以x=-2是原方程的解。
【剖析】方程兩邊同乘值為0的代數式,便產生增根。這一題錯解的原因是忘記驗根。當x=-2時,(x+2)(x-2)=0,所以x=-2是增根,原方程無解。
【正解】方程兩邊同乘(x+2)(x-2),得(x-2)2-(x+2)2=16。
解這個方程,得x=-2。
檢驗:當x=-2時,(x+2)(x-2)=0,x=-2是增根,原方程無解。
三、分式方程去分母時,整式部分易漏乘公分母
例3解方程
【錯解】方程兩邊同乘(x-3),得:
x-2=-1-2。
解這個一元一次方程,得x=-1。
檢驗:當x=-1時,x-3≠0,所以x=-1是原方程的解。
【剖析】這一題去分母時,違反了等式的基本性質,常數項-2漏乘了公分母(x-3)。
【正解】方程兩邊同乘(x-3),得:
x-2=-1-2(x-3)。
四、去分母,分子是多項式時漏加括號
例4解方程
【錯解】方程兩邊同乘3(x-3),得2x+9=12x-7+6(x-3)。
【剖析】去分母時,若分式的分子是一個多項式,應將多項式用括號括起來。這一題的錯誤在于未把分子上的4x-7用括號括起來。
【正解】方程兩邊同乘3(x-3),得:
2x+9=3(4x-7)+6(x-3),
解這個一元一次方程,得x=3。
檢驗:當x=3時,3(x-3)=0,x=3是增根,原方程無解。
五、分式方程化簡時,錯用分式的基本性質
例5解方程
【錯解】化簡,得
方程兩邊同乘(x-9),得x+4=2(x-9)。
解這個一元一次方程,得x=22。
檢驗:當x=22時,x-9≠0,x=22是原方程的解。
【剖析】此題化簡時用到分式的基本性質。分式的基本性質是分式的分子和分母都乘(或除以)同一個不等于0的整式,分式的值不變。這一題是分子乘2,而分母乘3,所以分式的值發生了改變。
【正解】化簡,得
方程兩邊同乘(2x-18),得3x+12=2(2x-18)。
解這個一元一次方程,得x=48。
檢驗:當x=48時,2x-18≠0,x=48是原方程的解。
六、分式方程“有增根”和“無解”易混為一談
例6當m為何值時,分式方程=0無解。
【錯解】方程兩邊同乘(x+2)(x-2),得:
2(x+2)+mx=0。
解得m1=-4,m2=0。
【剖析】“分式方程有增根”是指去分母后的整式方程的解使得分式方程的最簡公分母為0。而“分式方程無解”的原因有兩個:一是去分母后的整式方程無解;二是整式方程的解使得分式方程的最簡公分母為0。分式方程“有增根”是“無解”的一種情況。這一題錯把分式方程無解默認為是分式方程有增根了。
【正解】方程兩邊同乘(x+2)(x-2),得:
2(x+2)+mx=0。
①當x=2或x=-2時,
解得m1=-4,m2=0。
即:m=-2時,分式方程無解。
所以當m1=-4,m2=0,m3=-2時,分式方程無解。
七、求分式方程中字母的取值時,易忽略分母不為0
例7已知關于x的方程的解為正數,求m的取值范圍。
【錯解】方程兩邊同乘(x-3),得:
x=2(x-3)+m。
解這個一元一次方程,得x=6-m。
由原方程的解為正數,得x>0,即6-m>0。
解得m<6。
所以當m<6時,原方程的解為正數。
【剖析】解決這種問題時,不僅要考慮“方程的解為正數”這個條件,還要考慮x-3≠0這個隱含的條件。這一題的錯解就忽略了x-3≠0這個隱含的條件。
【正解】方程兩邊同乘(x-3),得:
x=2(x-3)+m。
解這個一元一次方程,得x=6-m。
由原方程的解為正數,得x>0,即6-m>0。
解得m<6。
又因為x-3≠0,得x≠3,即6-m≠3。
解得m≠3。
所以當m<6且m≠3時,原方程的解為正數。
小試牛刀
【參考答案】
1.原方程無解。