基于PUF的Logistic混沌序列發(fā)生器

黃春光，程海，丁群

?

基于PUF的Logistic混沌序列發(fā)生器

黃春光，程海，丁群

（黑龍江大學(xué)電子工程學(xué)院，黑龍江 哈爾濱 150080）

由于Logistic非線性混沌系統(tǒng)在一定的參數(shù)下，具有初值敏感性和拓撲復(fù)雜性等特點，因此Logistic混沌系統(tǒng)可以作為隨機序列信號發(fā)生器。同時由于集成電路在生產(chǎn)、制作的過程中，即使采用完全相同的設(shè)計方法和制造工藝，也會在器件上產(chǎn)生不可控的微小差異，這些微小差異便成為集成電路不可克隆的基礎(chǔ)。基于此特點，提出了一種基于可編程邏輯陣列（FPGA）的雙輸出查找表（LUT）結(jié)構(gòu)的物理不可克隆函數(shù)（PUF）的Logistic隨機混沌序列信號發(fā)生器，該混沌序列發(fā)生器具有物理的唯一性，能夠有效地抵抗對于系統(tǒng)的復(fù)制和攻擊。將該系統(tǒng)在Xilinx公司的FPGA開發(fā)板上進行測試和驗證，結(jié)果表明，同樣的電路結(jié)構(gòu)和配置文件在不同的FPGA開發(fā)板上能夠產(chǎn)生不同的隨機序列，提高了混沌序列的隨機性。

Logistic混沌系統(tǒng)；物理不可克隆函數(shù)；序列發(fā)生器；流密碼

1 引言

隨著通信技術(shù)的飛速發(fā)展及互聯(lián)網(wǎng)絡(luò)和移動網(wǎng)絡(luò)的廣泛使用，人們越來越關(guān)注信息的安全。混沌系統(tǒng)由于具有初值敏感性和拓撲復(fù)雜性等特點，得到了廣大研究人員的關(guān)注[1]。

混沌系統(tǒng)是指在一個確定性的系統(tǒng)中，存在著隨機的不規(guī)則運動，這種運動具有不確定性、不可重復(fù)性以及不可預(yù)測性，是非線性動力系統(tǒng)的固有特性。Logistic混沌映射是一種一維混沌系統(tǒng)，當該系統(tǒng)的參數(shù)在一定的范圍內(nèi)時，系統(tǒng)會進入混沌狀態(tài)。由于混沌特性的存在，Logistic混沌映射系統(tǒng)可以應(yīng)用在隨機信號發(fā)生器上。為了便于數(shù)字電路和FPGA應(yīng)用Logistic混沌系統(tǒng)，通常采用離散的Logistic混沌映射系統(tǒng)進行設(shè)計和開發(fā)[2-3]。由于離散混沌系統(tǒng)具有狀態(tài)隨機性和初值敏感性等特點，因此可以將其應(yīng)用到數(shù)字圖像加密[4]、隨機數(shù)發(fā)生器[5]以及數(shù)字認證等相關(guān)領(lǐng)域。

物理不可克隆函數(shù)（PUF, physical unclonable function）是一種對集成電路芯片在制造過程中產(chǎn)生的細微差異進行放大并使其產(chǎn)生獨一無二的物理不可克隆特征的函數(shù)。大多數(shù)物理不可克隆函數(shù)的實現(xiàn)是通過計算和分析電路的時延信息的差異進行設(shè)計的。想要對物理不可克隆函數(shù)模塊進行復(fù)制，需要復(fù)制相同的邏輯單元、相同的布局布線，同時在物理電路上進行精確的設(shè)計，才能得到相同的結(jié)果。但是對于具體的物理電路而言，電路結(jié)構(gòu)和布局布線的差異是由電路自身的物理參數(shù)決定的，無法進行克隆復(fù)制，因此物理不可克隆函數(shù)提供了一種可以在相同的電路結(jié)構(gòu)上產(chǎn)生不同的差異的模塊。由于PUF具有基于器件特征的固有隨機性，很多研究人員將PUF應(yīng)用到設(shè)備的認證環(huán)節(jié)[6]和通信環(huán)節(jié)[7]。

可編程邏輯陣列（FPGA, field-programmable gate array）是一種可編程的芯片，能夠根據(jù)用戶的需求通過軟件手段進行更改、配置內(nèi)部連接結(jié)構(gòu)和邏輯單元、完成指定設(shè)計功能的數(shù)字電路。由于可編程邏輯陣列具有開發(fā)簡單方便、實現(xiàn)效率高等優(yōu)點，已廣泛應(yīng)用到電路設(shè)計、嵌入式系統(tǒng)等各個領(lǐng)域。在進行可編程邏輯陣列應(yīng)用開發(fā)的過程中，可以使用芯片提供商提供的開發(fā)軟件進行邏輯電路的設(shè)計和仿真，然后下載到可編程邏輯陣列中。在使用過程中，可以將生成的比特流數(shù)據(jù)下載到相應(yīng)的邏輯電路中，完成對于系統(tǒng)的配置。由于電路結(jié)構(gòu)相同，可以將相同的比特流下載到不同的FPGA邏輯電路中，得到相同的功能。由于物理不可克隆函數(shù)的存在，即使相同的配置文件，也會產(chǎn)生不同的結(jié)果，因此可以對設(shè)備進行識別和身份確認。

FPGA具有配置靈活、設(shè)計方便等特點，非常適合電路設(shè)計。Dabal等[8]利用Xilinx公司的FPGA設(shè)計了基于Logistic混沌系統(tǒng)的隨機序列，作為流密碼發(fā)生器。Wang等[9]利用Simulink工具設(shè)計了基于FPGA的混沌序列信號發(fā)生器，并對相關(guān)性進行分析。但是，由于數(shù)字Logistic混沌系統(tǒng)產(chǎn)生的序列和器件結(jié)構(gòu)無關(guān)，因此容易被復(fù)制、攻擊和探測。基于此，本文設(shè)計了一種基于物理不可克隆函數(shù)的Logistic混沌序列發(fā)生器，利用FPGA硬件結(jié)構(gòu)的細微差異產(chǎn)生基于器件特征的混沌隨機序列，并利用FPGA中的基本單元——查找表（LUT, look-up-table）在不同器件上傳輸時延的細微差異進行設(shè)計，所產(chǎn)生的混沌序列與物理器件相關(guān)，相同的電路在不同的FPGA器件上可以產(chǎn)生完全不同的結(jié)果。該系統(tǒng)可以作為安全設(shè)備的終端，利用在服務(wù)器上存儲的硬件特征完成設(shè)備的驗證或數(shù)據(jù)的加密傳輸。

2 相關(guān)工作

2.1 國內(nèi)外發(fā)展

目前，在通信領(lǐng)域、視頻傳輸、網(wǎng)絡(luò)通信和個人消費電子產(chǎn)品等相關(guān)領(lǐng)域都需要基于FPGA加密技術(shù)的數(shù)字認證環(huán)節(jié)[10]。Wang等[11]提出了一種基于FPGA公鑰與私鑰對的知識產(chǎn)品保護方案。Guajardo等[12]設(shè)計了一種基于PUF的加密認證系統(tǒng)。Tuncer等[13]利用Logistic混沌系統(tǒng)作為PUF的初始隨機向量，然后對Logistic混沌系統(tǒng)的輸出進行判斷，產(chǎn)生“0”和“1”的隨機序列。該系統(tǒng)采用Logistic信號發(fā)生器作為PUF的隨機輸入。由于PUF的狀態(tài)有限，沒有充分利用混沌系統(tǒng)的狀態(tài)隨機性和初值敏感性，而且該系統(tǒng)的PUF模塊在四輸入單輸出的LUT模塊上實現(xiàn)，利用率低，因此只對該系統(tǒng)在單個開發(fā)板上進行了測試，沒有將其應(yīng)用到其他開發(fā)板，以測試PUF的特性。Liu等[14]給出了一種基于碳納米管的物理不可克隆函數(shù)，采用的混沌方程為Lorenz混沌方程，利用碳納米管工藝的不確定性，生成PUF。但是由于碳納米管生成的序列位數(shù)有限，而且采用模擬電路進行設(shè)計，不利于大規(guī)模開發(fā)和使用。

2.2 物理不可克隆函數(shù)

自2002年以來，人們對基于硅電路的PUF電路進行了深入的研究。到目前，研究人員已經(jīng)提出了各種物理不可克隆的方法，例如，基于隨機存儲器的PUF、基于觸發(fā)器的PUF、基于蝴蝶類型的PUF、基于仲裁器的PUF、基于環(huán)形振蕩器的PUF[15]、基于電路毛刺的PUF[16]等。產(chǎn)生PUF的方法，大體上可以分為2種，介紹如下。

一種為采用隨機存儲的方式設(shè)計的PUF電路。由于存儲電路是由一種狀態(tài)可以改變的雙穩(wěn)態(tài)電路組成的，因此存儲電路在通電之前會處于一種隨機狀態(tài)。存儲電路在通電之后，寄存器上的狀態(tài)是一種隨機狀態(tài)，此時存儲電路上的高低電平可以作為PUF使用。但是對于芯片設(shè)計廠商來說，為了避免這種狀態(tài)的出現(xiàn)，在電路通電之后，會進行強制復(fù)位。只有在設(shè)計電路時進行單獨設(shè)計，才能夠使用。

另一種為采用時延的方式設(shè)計的PUF，利用物理器件上門電路的時延和布線的時延差異進行設(shè)計。在實現(xiàn)方式上，主要分為2種，一種是仲裁型PUF，另一種是環(huán)形振蕩器PUF。

1) 仲裁型PUF

采用2路相同的傳輸路徑，由于集成電路制造工藝的細微差異會產(chǎn)生不同的時延，判決器根據(jù)2路傳輸路徑到達時間的差異決定輸出是“0”還是“1”，從而產(chǎn)生基于器件自身特點的隨機信號。仲裁型PUF的控制端控制信號傳輸?shù)穆窂剑到y(tǒng)輸入端輸入同一個脈沖信號，利用控制信號進行路徑選擇，使信號經(jīng)過不同的傳輸路徑，根據(jù)信號到達仲裁器的先后順序進行判決。

在PUF設(shè)計過程中，需要盡量保證傳輸路徑的長度一致，但是由于物理元件的差異，最終會導(dǎo)致同一個脈沖到達仲裁器的時間不盡相同。如圖1所示，仲裁類型PUF利用控制信號（0,1,…）選擇信號傳輸?shù)穆窂剑斎氲氖峭粋€脈沖信號，經(jīng)過不同的路徑到達仲裁器，仲裁器根據(jù)脈沖信號到達的先后順序進行判決，決定輸出是“0”還是“1”。這類PUF需要的多路選擇器級別多、路徑長，否則無法分辨到達的先后順序，即使能夠判決，也容易被外界環(huán)境干擾。

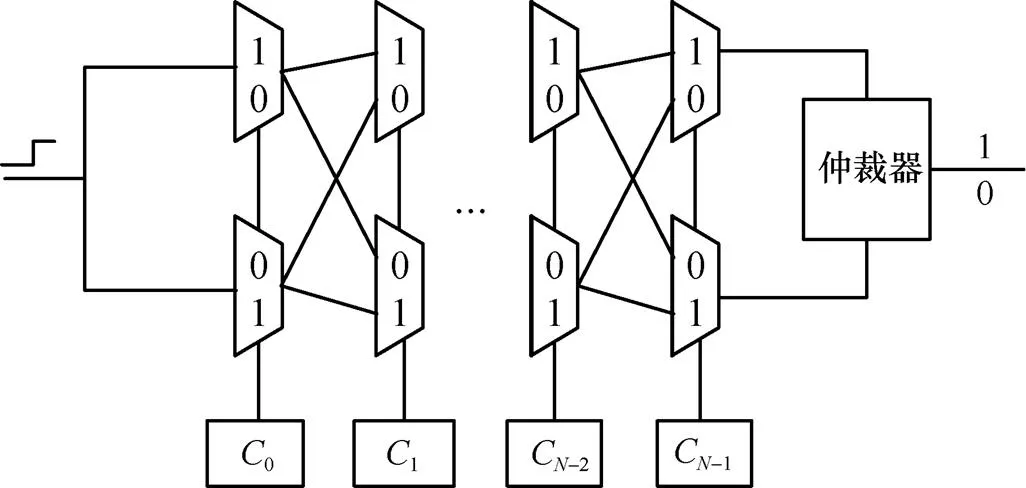
圖1 仲裁型PUF

2)環(huán)形振蕩器PUF

利用反相器級聯(lián)形成振蕩電路，通過計數(shù)器進行計數(shù)。由于物理電路結(jié)構(gòu)的微小差異，經(jīng)過多次計數(shù)，2個計數(shù)器的結(jié)果不盡相同，然后通過比較器，得到最終的結(jié)果。

圖2中與門作為控制端，控制環(huán)形振蕩器PUF的起振和停止。與門和后面的多個反相器相連接，構(gòu)成一個連續(xù)反向的環(huán)。該環(huán)形振蕩器產(chǎn)生的脈沖信號作為計數(shù)器的時鐘，進行計數(shù)。計數(shù)器設(shè)定計數(shù)的截止上限，當其中任意一個計數(shù)器計數(shù)達到上限，則環(huán)形振蕩器停止工作。在進行布局布線過程中，要求保證路徑長度一致。比較器通過比較2個計數(shù)器數(shù)值的大小，輸出“0”或“1”。

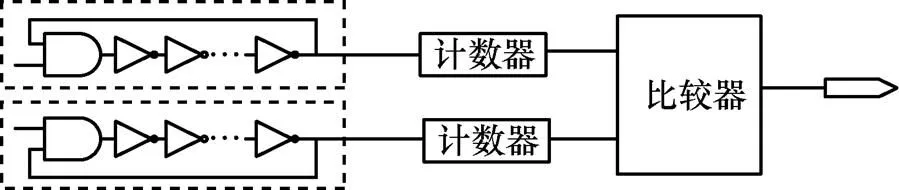
圖2 環(huán)形振蕩器PUF

在環(huán)形振蕩器PUF中，如果反相器的個數(shù)為奇數(shù)，需要使用與門作為控制模塊，控制環(huán)形振蕩器的工作狀態(tài)；如果環(huán)形振蕩器中反相器的個數(shù)為偶數(shù)，則采用與非門作為控制模塊。

環(huán)形振蕩器PUF所需的與非門的個數(shù)少，相對仲裁型PUF來說占用資源少，外界環(huán)境影響小。

2.3 Logistic混沌方程

Logistic方程為混沌系統(tǒng)的經(jīng)典實例，系統(tǒng)結(jié)構(gòu)簡單，便于FPGA設(shè)計、實現(xiàn)和驗證，同時便于推廣到其他混沌系統(tǒng)。

Logistic函數(shù)的數(shù)學(xué)表達式為

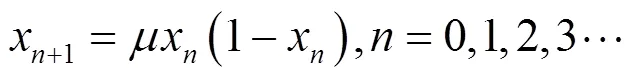
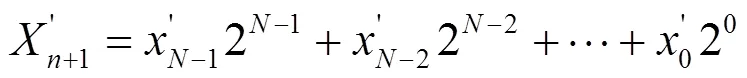
式(2)是Logistic方程的二進制表現(xiàn)形式。其中，為二進制的表現(xiàn)形式，是二進制每一位的值。的位數(shù)越大，Logistic方程的精度越好，同時需要的運算量就越大。

3 系統(tǒng)設(shè)計

基于環(huán)形振蕩器的PUF，利用有限個數(shù)的反相器，構(gòu)建一個反饋鏈。基于仲裁型的PUF，可以利用控制位選擇相應(yīng)的路徑，根據(jù)判決器的結(jié)果產(chǎn)生“0”或“1”。本文提出基于混合型PUF的Logistic序列發(fā)生器，同時利用環(huán)形振蕩器PUF與仲裁型PUF的特點，產(chǎn)生基于物理器件特征的隨機數(shù)。利用Logistic混沌方程對系統(tǒng)初值的敏感性（如圖3所示），初值的細微差異會產(chǎn)生完全不同的變化軌跡。利用Logistic方程的特點，將PUF與Logistic迭代方程相結(jié)合，既利用PUF的硬件唯一性，又利用Logistic函數(shù)的敏感性，產(chǎn)生與硬件相關(guān)的混沌序列，同時在Xilinx公司的7-series FPGA上進行設(shè)計和驗證。

3.1 基本單元模塊

本文采用FPGA進行設(shè)計和開發(fā)。由于FPGA具有大量的可編程資源，為系統(tǒng)的實現(xiàn)提供了相應(yīng)的功能模塊，既解決了定制電路的不足，又克服了原有可編程器件門電路有限的缺點。Xilinx公司的FPGA具有6輸入2輸出的LUT模塊，有利于多輸入多輸出的應(yīng)用模塊設(shè)計。

Xilinx公司的7-series FPGA的基本單元為CLB，每個CLB由2個SLICE組成，每個SLICE由4個5輸入的LUT、3個MUX、一個CARRY和8個FF組成。

如圖4所示，Xilinx公司7-series FPGA的每個LUT有6個輸入端口，當A6設(shè)置為高電平時，可以作為2個5輸入的LUT使用，可以有2個輸出。在設(shè)計過程中，需要對LUT6_2模塊進行配置，將其配置為2輸入2輸出的與門電路和2輸入2輸出的非門電路。

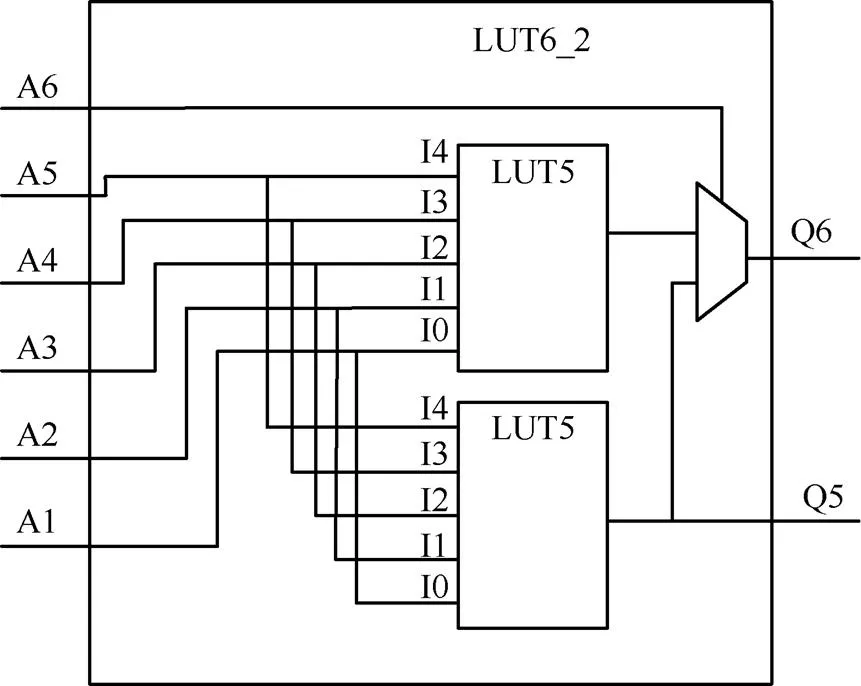
圖4 FPGA的基本單元LUT6_2

對于圖5中的2輸入2輸出非門電路，即圖中虛線內(nèi)部的模塊，可以用一個LUT6_2進行設(shè)計。可以充分利用LUT6_2的2個輸出的特性，將A6設(shè)置為高電平，而A5和A4輸入沒有使用，可以配置高電平或低電平，不能懸空使用。在本設(shè)計中，A4和A5設(shè)置為低電平，這樣就可以使用Q5和Q6這2個輸出，則電路等效如圖5所示。

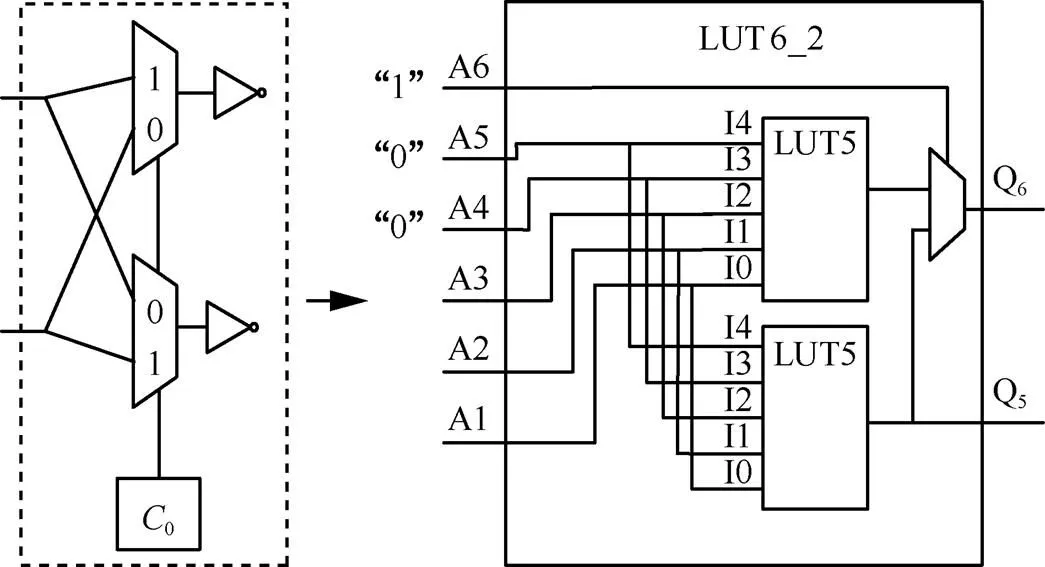
圖5 基于LUT6_2的雙路非門電路

每個模塊有3個輸入，其中，A3作為選擇信號，A2和A1作為數(shù)據(jù)的2個輸入端口，此時，該電路模塊為3輸入2輸出的功能模塊。根據(jù)真值表進行計算，可以得到LUT6_2的配置碼為0x0000c0a0_0000a0c0，此時LUT可實現(xiàn)雙路非門和路徑選擇的功能。

同理，將LUT6_2設(shè)計為2輸入2輸出的與門時，每個模塊有4個輸入，其中，A6為高電平，A5為低電平，A4作為使能信號，A3作為選擇信號，A2和A1作為數(shù)據(jù)的2個輸入端口，則根據(jù)電路的功能設(shè)置相應(yīng)LUT的數(shù)值。根據(jù)真值表進行計算，可以得到LUT6_2的配置碼為0x00000035_ 00000053，此時LUT可以實現(xiàn)雙路與門及路徑選擇的功能，如圖6所示。

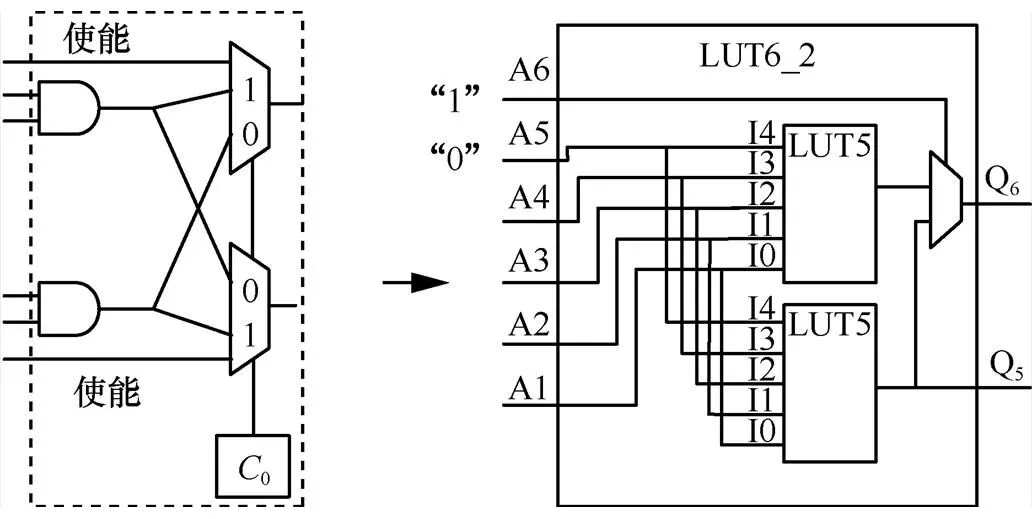
圖6 基于LUT6_2的雙路與門電路

3.2 系統(tǒng)框圖

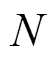
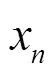
圖8 系統(tǒng)工作流程

系統(tǒng)工作狀態(tài)機如圖9所示，分為5個步驟。

圖9 系統(tǒng)工作狀態(tài)機

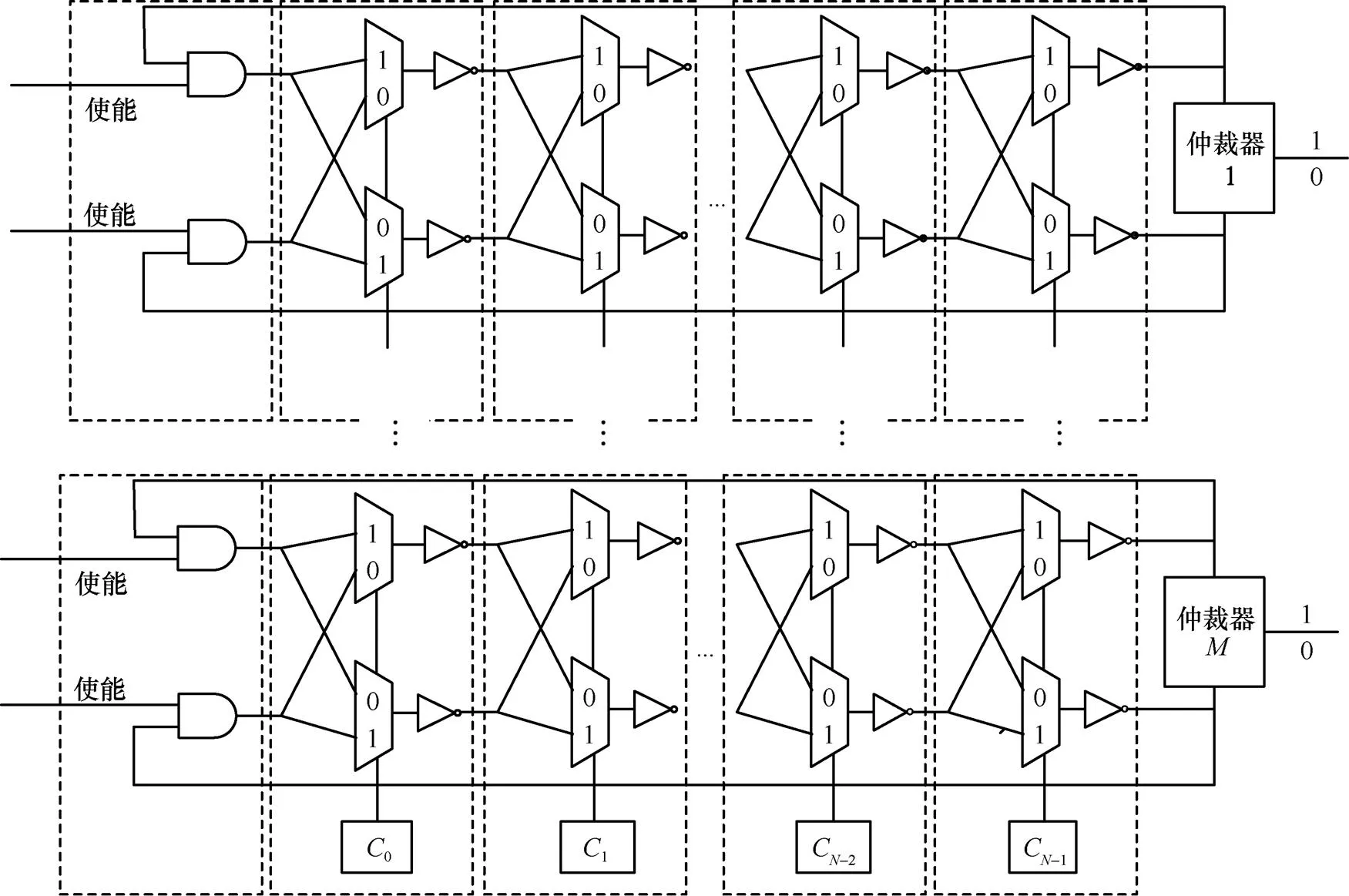
圖7 系統(tǒng)框圖

步驟1 設(shè)置系統(tǒng)的初值，PUF的結(jié)構(gòu)有個控制端，用來選擇PUF的不同路徑。由于PUF的特點，不同的PUF所產(chǎn)生的結(jié)果不完全一樣。

步驟2 利用PUF模塊生成bit，將bit傳遞給Logistic混沌系統(tǒng)。

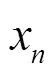
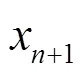
4 系統(tǒng)分析與測試

在本文系統(tǒng)中，由于PUF的存在，使原來混沌系統(tǒng)無法迭代到的點重新成為系統(tǒng)的初值，破壞了離散混沌系統(tǒng)的周期性，為了測試基于PUF的Logistic混沌序列發(fā)生器的特性，采用Xilinx公司的7-series FPGA開發(fā)板進行測試，并對序列發(fā)生器的相關(guān)特性進行了分析和討論。

4.1 實驗環(huán)境

本文在Xilinx公司的7-series FPGA上設(shè)計了基于物理不可克隆函數(shù)的Logistic混沌序列發(fā)生器，設(shè)計軟件采用Xilinx公司的vivado 2017.4版本進行設(shè)計開發(fā)，并利用vivado自帶邏輯分析儀進行數(shù)據(jù)測試和分析。在實驗過程中，對4塊同樣的FPGA開發(fā)板進行測試，通過XDC文件對模塊的具體位置和走線利用約束條件進行限定，同時將PUF布置到FPGA的不同位置進行測試。

本系統(tǒng)利用LUT6_2設(shè)計了32路PUF，通過對32路PUF的計數(shù)器輸出的數(shù)值進行比較，得到32 bit的輸出。

4.2 實驗數(shù)據(jù)

在實驗過程中，同樣的配置代碼在不同的FPGA開發(fā)板上的結(jié)果并不相同。首先，相同的Logistic初始向量作用到PUF上，不同的開發(fā)板得到的結(jié)果如表1所示，結(jié)果呈現(xiàn)出隨機性。

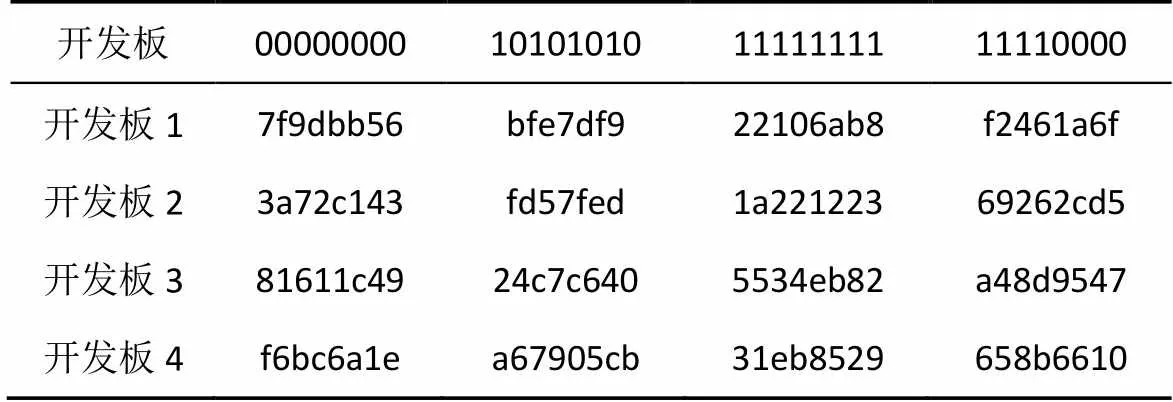
表1 不同開發(fā)板在相同配置下的輸出結(jié)果

系統(tǒng)的硬件開銷如表2所示。由于系統(tǒng)采用LUT6_2的單元電路，每個單元模塊包括6個輸入和2個輸出，因此每個LUT模塊可以實現(xiàn)2路PUF電路，由于LUT模塊具有6個輸入端口，可以選擇其中一個端口作為控制端口，使得硬件的利用率得到提升。Tuncer等[13]使用LUT4_1模塊，每個模塊可以實現(xiàn)一路PUF電路，利用率低。

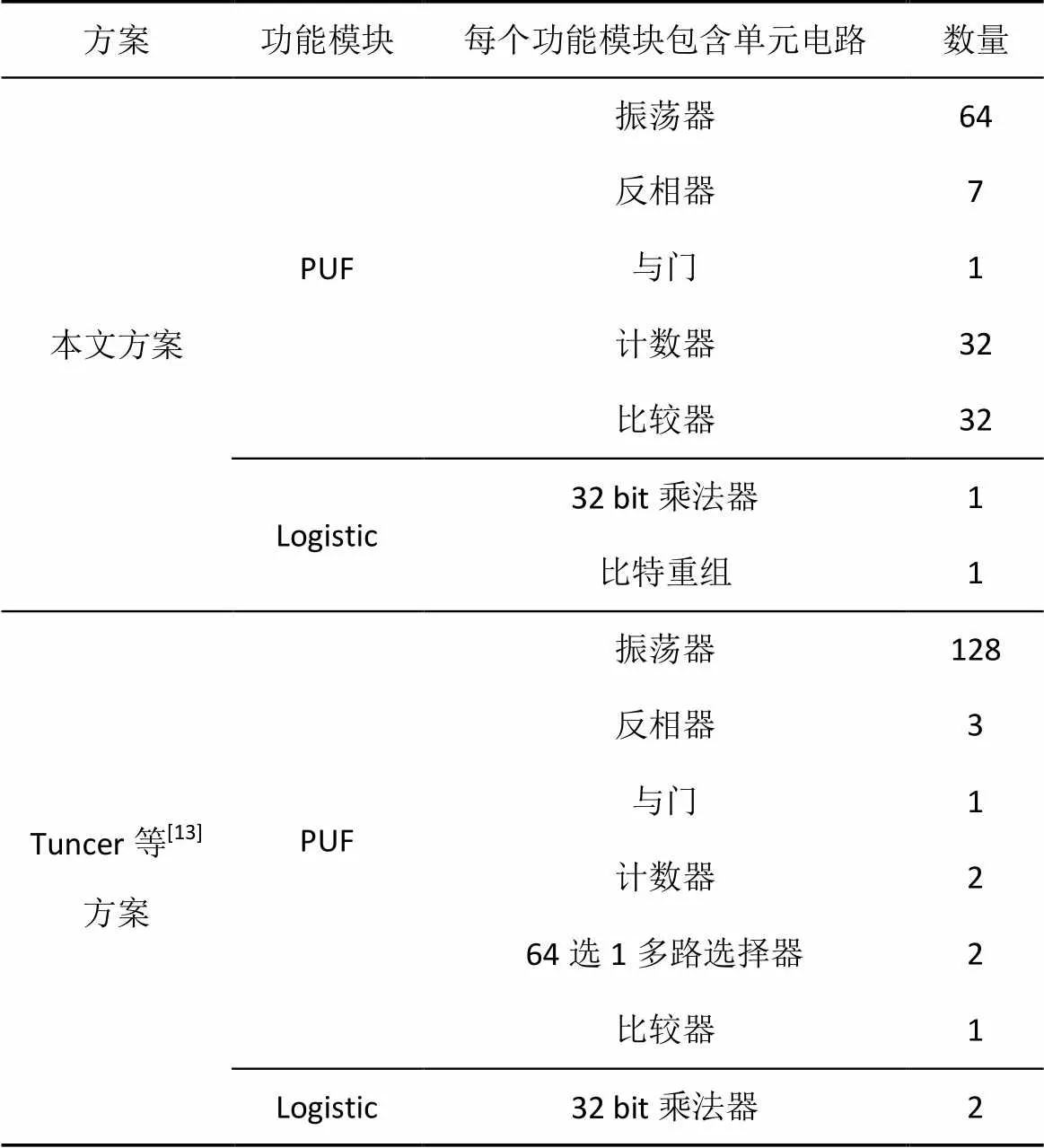
表2 硬件開銷說明

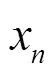
圖10 PUF單元的布局布線

4.3 數(shù)據(jù)分析

4.3.1 相關(guān)性分析

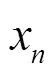
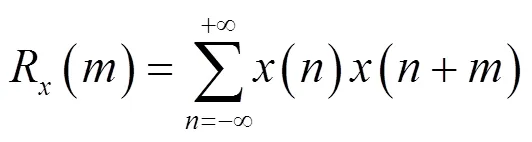
通過對混沌序列發(fā)生器的輸出進行分析和設(shè)計，對于原始的Logistic混沌系統(tǒng)，采用32 bit的精度進行計算，自相關(guān)函數(shù)如圖11所示，對于不同的Logistic初值，系統(tǒng)會出現(xiàn)一些周期現(xiàn)象。

如果采用基于PUF的Logistic混沌系統(tǒng)進行設(shè)計，可以阻止Logistic混沌系統(tǒng)周期現(xiàn)象的出現(xiàn)。同時，由于PUF系統(tǒng)的存在，使Logistic混沌軌道上無法迭代到的點可以成為系統(tǒng)的初值進行計算，改善了系統(tǒng)的周期性，如圖12所示，系統(tǒng)不存在明顯的周期性現(xiàn)象。

4.3.2 隨機性分析

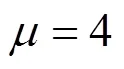
圖12 基于PUF的Logistic序列自相關(guān)函數(shù)

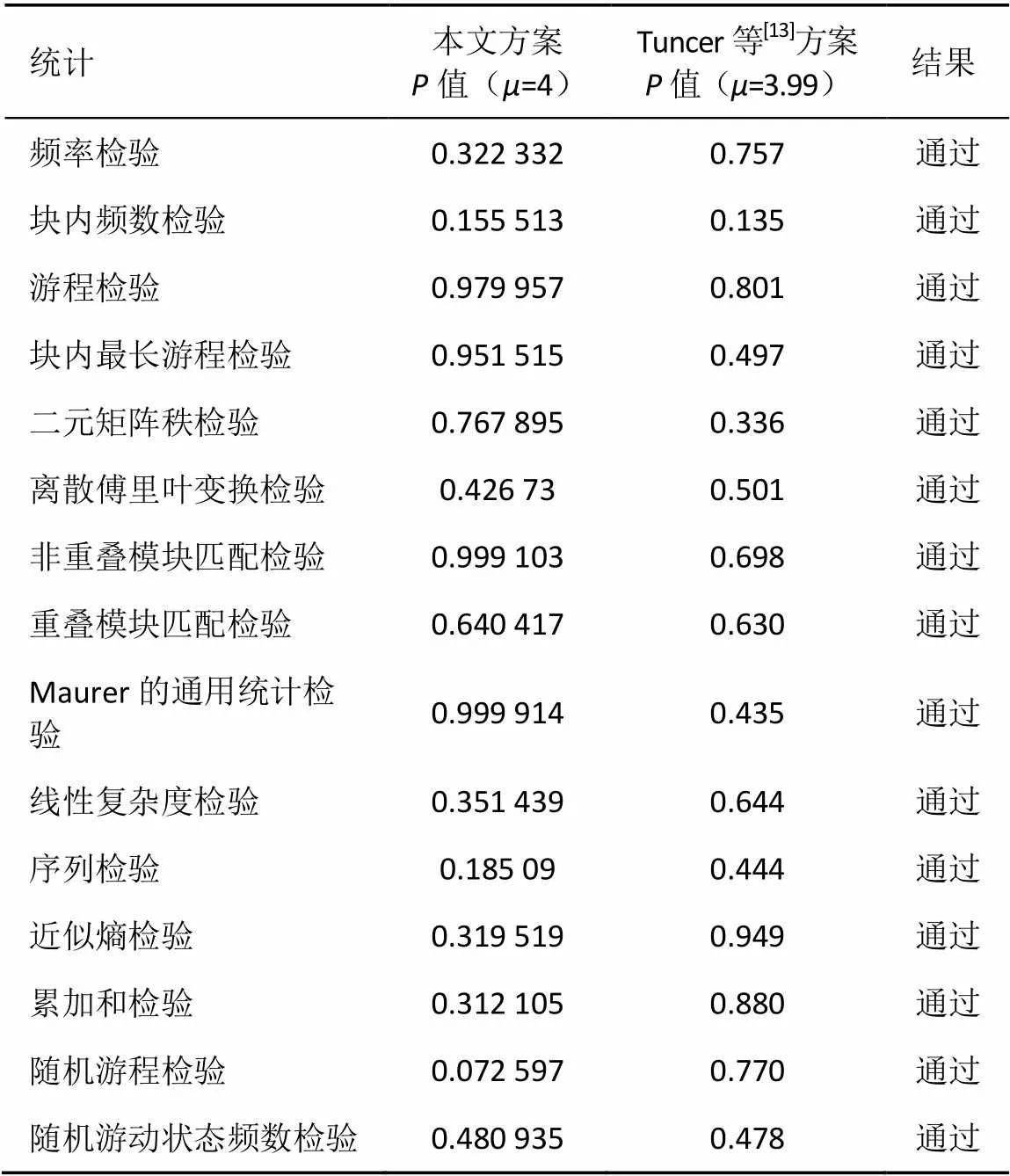
表3 評價指標P值的對比結(jié)果

5 結(jié)束語

本文提出了一種基于物理不可克隆函數(shù)（PUF）的Logistic混沌序列發(fā)生器，利用FPGA器件的LUT以及傳輸路徑在生產(chǎn)過程中的工藝差異進行設(shè)計，所以即使同樣配置碼下載到不同的FPGA開發(fā)板上，產(chǎn)生的結(jié)果也不同。首先利用Xilinx的FPGA中的LUT6_2設(shè)計了2路PUF結(jié)構(gòu)，相對于傳統(tǒng)的FPGA而言，節(jié)省了一半的資源；然后利用PUF產(chǎn)生的隨機數(shù)對Logistic混沌系統(tǒng)進行優(yōu)化，設(shè)計了Logistic混沌序列信號發(fā)生器。該序列發(fā)生器產(chǎn)生的序列與物理器件的特性相關(guān)，利用物理器件的特征參數(shù)作為序列發(fā)生器的原始密鑰，保證了序列發(fā)生器的唯一性。NIST檢驗表明，混沌序列信號發(fā)生器產(chǎn)生的序列滿足隨機性的要求。

[1] SBIAA F, BAGANNE A, ZEGHID M, et al. A new approach for encryption system based on block cipher algorithms and Logistic function[C]//International Multi-Conference on Systems, Signals & Devices. 2015: 1-5.

[2] KANSO A, SMAOUI N. Logistic chaotic maps for binary numbers generations[J]. Chaos Solitons & Fractals, 2009, 40(5): 2557-2568.

[3] 蔡丹, 季曉勇, 史賀, 等. 改進分段 Logistic混沌映射的方法及其性能分析[J]. 南京大學(xué)學(xué)報(自然科學(xué)), 2016, 52(5): 809-815. CAI D, JI X Y, SHI H, et al. Method for improving piecewise Logistic chaotic map and its performance analysis[J]. Journal of Nanjing University, 2016, 52(5): 809-815.

[4] XU L, LI Z, LI J, et al. A novel bit-level image encryption algorithm based on chaotic maps[J]. Optics & Lasers in Engineering, 2016, 78(21): 17-25.

[5] 宣蕾, 閆紀寧. 基于混沌的“一組一密”分組密碼[J]. 通信學(xué)報, 2009, 30(Z2): 105-110.XUN L, YAN J N. The “one group one cipher” cryptograph of block cipher based on chaotic[J]. Journal on Communications, 2009, 30(Z2): 105-110.

[6] 王俊, 劉樹波, 梁才, 等. 基于PUF和IPI的可穿戴設(shè)備雙因子認證協(xié)議[J]. 通信學(xué)報, 2017, 38(6): 127-135. WANG J, LIU S B, LIANG C, et al. Two-factor wearable device authentication protocol based on PUF and IPI[J]. Journal on Communications, 2017, 38(6): 127-135.

[7] 郭淵博, 張紫楠, 楊奎武. 基于PUFS的不經(jīng)意傳輸協(xié)議[J]. 通信學(xué)報, 2013, 34(Z1): 38-43. GUO Y B, ZHANG Z N, YANG K W. Oblivious transfer based on physical unclonable function system[J]. Journal on Communications, 2013, 34(Z1): 38-43.

[8] DABAL P, PELKA R. FPGA implementation of chaotic pseudo-random bit generators[C]//Mixed Design of Integrated Circuits and Systems. 2012: 260-264.

[9] WANG H J, SONG B, LIU Q, et al. FPGA design and applicable analysis of discrete chaotic maps[J]. International Journal of Bifurcation & Chaos, 2014, 24(4): 917-921.

[10] ADAMO O, MOHANTYZ S P, KOIUGIANOS E, et al. VLSI architecture and FPGA prototyping of a digital camera for image security and authentication[C]//Region 5 Conference. 2006: 154-158.

[11] WANG Y, RENFA L I. FPGA based unified architecture for public key and private key cryptosystems[J]. Frontiers of Computer Science, 2013, 7(3): 307-316.

[12] GUAJARDO J, KUMAR S S, SCHRIJEN G J, et al. FPGA intrinsic PUFs and their use for IP protection[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2007: 63-80.

[13] TUNCER T. The implementation of chaos-based PUF designs in field programmable gate array[J]. nonlinear dynamics, 2016, 86(2): 1-12.

[14] LIU L, HUANG H, HU S. Lorenz chaotic system based carbon nanotube physical unclonable functions[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2017, PP(99): 1.

[15] KUMAR S. The buttefly PUF : protecting IP on every FPGA[C]//IEEE International Workshop on Hardware Oriented Security and Trust. 2008.

[16] 龐子涵, 周強, 高文超, 等. 高效能FPGA毛刺PUF設(shè)計與實現(xiàn)[J]. 計算機輔助設(shè)計與圖形學(xué)學(xué)報, 2017, 29(6): 1135-1144. PANG Z H, ZHOU Q, GAO W C, et al. Design and implementation of high efficiency PUF circuit on FPGA[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(6): 1135-1144.

[17] CHENG H, SONG Y, HUANG C, et al. Self-adaptive chaotic Logistic map: an efficient image encryption method[J]. Journal of Internet Technology, 2016, 17(4): 743-752.

Logistic chaotic sequence generator based on physical unclonable function

HUANG Chunguang, CHENG Hai, DING Qun

Electronic Engineering College of Heilongjiang University, Harbin 150080, China

Logistic nonlinear chaotic system has many good characters such as initial value sensitivity and topological mixing in the some parameter condition, which is used to create the random sequence signal generator. Because of the attributions of randomness and uniqueness even under the exact, the same circuit layouts and manufacturing procedures, there is still an instinct unclonable difference in each integrated circuit. Therefore, a new sequence stream generator was proposed based on Logistic chaotic system and physical unclonable function designed by double output look-up-table (LUT). The output of the Logistic sequence generator was associated with a specific physical circuit. This kind of sequence generator could resist an attack such as the replication of the keys of the system. The system was designed and tested on the Xilinx FPGA board. The results show that the same architecture of the circuit and the same config file operated on the different FPGA developing board can generate the total different random chaotic sequence stream and improve the randomness of the stream.

Logistic chaotic system, physical unclonable function, random number generator, stream ciphe

TP301

A

10.11959/j.issn.1000?436x.2019064

2018?05?14；

2018?08?16

丁群，qunding@aliyun.com

國家自然科學(xué)基金資助項目（No. 61471158, No.61571181）

The National Natural Science Foundation of China (No.61471158, No.61571181)

黃春光（1980? ），女，黑龍江哈爾濱人，黑龍江大學(xué)講師，主要研究方向為保密通信、信息安全。

程海（1979? ），男，黑龍江哈爾濱人，黑龍江大學(xué)副教授、碩士生導(dǎo)師，主要研究方向為保密通信、信息安全。

丁群（1957? ），女，黑龍江哈爾濱人，黑龍江大學(xué)教授、博士生導(dǎo)師，主要研究方向為保密通信、信息安全。