非均勻加熱管內單相流動傳熱特性數值模擬

， ，

(中國船舶重工集團有限公司第七○三研究所，哈爾濱 150078)

0 引 言

管路內單相流體的流動與傳熱現象在動力、化工、核能、制冷、石油及航天等現代工業中廣泛存在。例如，火電站和核電站中的各種熱交換器，化學工程和制冷設備中的各式蒸發器和冷凝器，以及宇航工業中的火箭推進系統等等。這些動力系統或設備的運行狀況都與流動和傳熱過程有關，其優化設計、經濟技術指標的提高以及安全性的保障，客觀上要求準確掌握相關的流動和傳熱方面的各種知識[1]。前人也對均勻加熱管內流動與傳熱特性進行了深入研究，發展了一系列的傳熱系數及壓降的關聯式[2-3]，為實際工程應用提供了理論依據。

在某些特殊場合，管路受熱是不均勻的，如電廠中的鍋爐水冷壁、核反應堆的管式換熱器、太陽能發電系統熔鹽吸熱器等，均是一側受熱，而另一側絕熱。楊敏林[4]數值計算了半周加熱熔鹽吸熱管在高溫、高熱流密度條件下的管內流速和溫度分布規律及其換熱特性，為塔式太陽能熱發電熔鹽吸熱器的設計和運行提供重要依據。胡志宏[5]采用半周鍍銀方法，試驗研究了超臨界及近臨界區垂直及傾斜圓管內傳熱特性及臨界熱負荷特性。Lekakh[6]研究了半周加熱對管內壓降的影響，認為管外非均勻加熱對管內壓降影響不大。Dedov[7]研究了半周加熱管內單相流體換熱特性，認為非均勻加熱管內的平均換熱系數依然可以采用Dittus-Boelter公式。另外Boscary[8]、Olekhnovitch[9]、Ami[10]幾位學者對低壓、大熱流密度下半周加熱管內的臨界熱負荷特性開展了研究，給出了相應的臨界熱負荷預測關聯式。然而，對于中高壓情況下流體流速、壁厚、溫度對半周加熱管內的熱流量分配及單相換熱特性和摩擦壓降特性的影響規律目前還沒有文獻報道。

由于半周加熱的實現方式比較困難，而且通過實驗的方法很難確定流體在管內的具體流動情況，加上實驗的方法在經濟性和安全性等方面存在一些問題，所以數值模擬作為一種實驗研究的替代方法獲得了廣泛的應用。文中利用計算流體力學的方法，對不同熱流密度、不同管內工質流速、不同壁厚時壁溫分布及加熱側與絕熱側的熱流量比值進行了計算，分析了熱負荷非均勻分布對管內換熱系數及壓降的影響，為圓管換熱器設計和運行提供理論依據。

1 數理模型及數值方法

1.1 控制方程

采用Fluent軟件進行數值模擬時，對管內流動做如下假設：

(1)管壁加熱側熱流密度恒定且均勻；

(2)流動為穩態流動；

(3)管內為強制對流。

流場的控制方程為：

(1)連續方程：

(2)動量方程：

(3)能量方程：

1.2 物理模型

為模擬半周加熱對壁面及管內流體溫度分布的影響，我們建立了如下傳熱模型，如圖1所示。模型半周接受恒定且均勻的熱流密度，另外半周處于絕熱狀態。加熱側熱流密度范圍為600～2 000 kW/m2。過冷水由管道入口流入，加熱到接近飽和溫度時流出管道，其入口壓力為10 MPa，入口溫度為373 K，入口流速范圍為0.5～3 m/s。水在受熱管道中的物性隨著溫度的升高不斷變化，其密度(kg/m3)、定壓比熱(J/kg/K)、運動粘度(kg/m/s)及導熱系數(W/m/K)隨溫度的變化規律為：

管道結構參數包括內徑8 mm，外徑12～14 mm，壁厚2～3 mm。受熱管材料為316不銹鋼，其密度為7 930 kg/m3，定壓比熱為460 J/kg/K，導熱系數(W/m/K)隨壁面溫度不斷發生變化：

λ=0.014 886T+14.408

圖1 傳熱模型

1.3 數值方法

管內工質的流動是一個處于紊流狀態的三維穩態流動，其換熱過程包括熱傳導及熱對流兩種形式。因此，數值模擬的計算域為壁厚和流體流過的區域，控制方程為三維流動的連續方程及N-S動量及能量方程，湍流模型k-ε采用標準湍流模型，壓力-速度耦合采用Simple算法，對流插值采用QUICK格式。

模型網格采用四面體網格，設置合適的步長，節點數共279 720個。入口為速度入口，出口為OUTFLOW，加熱側為熱流邊界，絕熱側熱流密度為0，內壁面為耦合邊界。計算在整個區域進行，迭代次數設為1 000次，經過約400次的迭代計算收斂。

2 結果分析與討論

2.1 半周加熱管道不同位置處的壁溫分布情況

對壁厚為3 mm，熱流密度為1 000 kW/m2，速度為3 m/s時半周加熱管道入口、中間及出口處的溫度分布情況進行了計算。

由圖2可以看出，從管道入口到出口，流體溫度逐漸升高，絕熱側壁面溫度也隨之升高，兩側壁溫不均勻程度降低。這是由于隨著流體溫度升高，對流換熱溫差變小，加熱側通過對流換熱作用進入流體的熱量逐漸減少，而通過導熱作用傳導到絕熱側的熱量越來越多，因此兩側不均勻程度逐漸降低。

2.2 熱流量比值的影響規律

對壁厚為3 mm，熱流密度為1 000、2 000 kW/m2，速度為1、2、3 m/s時管道出口處的溫度分布情況及兩側平均熱流量比值進行了計算。

由圖3可以看出，熱流密度一定時，流速越高不均勻度越高。這是因為管內流速越高，管內對流換熱效果越強，加熱側的熱量主要通過對流換熱進入管內流體，向絕熱側導熱量則相對減小，因此流速越高，兩側熱流量比值越高。當熱流密度增加一倍時，隨著流速的變化兩側熱流量比值變化趨勢相同。速度相同時，兩側熱流量比值隨熱流密度的升高稍有增加，這是因為熱流密度越高，加熱側壁溫越高，壁面導熱系數隨之稍有增大，因此熱量從加熱側進入流體的比例增大。

對壁厚為2 mm，熱流密度為1 000 kW/m2、2 000 kW/m2，速度為1、2、3 m/s時管道出口處的溫度分布情況及兩側平均熱流量比值進行了計算。

圖2 半周加熱管道不同位置處的壁溫分布情況

圖3 熱量密度及速度對壁面溫度分布及熱流量比值的影響(左：壁厚3 mm,右：壁厚2 mm)

與壁厚為3 mm時相同，熱流量比值隨管內工質流速增加而增加，而熱流密度對熱流量比值的影響則不大。

將上述幾種工況下兩側熱流量比值整理列入表1。由表1可以看出，壁厚為2 mm比壁厚為3 mm時不均勻程度增強。這是由于壁厚值越小，加熱側由外壁面進入流體的總熱阻越小，熱量主要通過加熱側進入工質，通過導熱進入絕熱側的熱量減小，兩側熱流量比值增加。從表1還可以看出，流速越大，壁厚對熱流量比值的影響越明顯。這是因為主要熱阻在于壁面導熱，流速越大，管內對流換熱熱阻越小，導熱熱阻對整個換熱的影響越顯著。因此流速越大，改變壁面熱阻對壁面兩側熱流量比值的影響越明顯。

下面將以符號ψ表示平均熱流量比值。取下面參數范圍內兩側壁面熱流量比值的平均值，以方便對傳熱系數進行修正：壁厚為2 mm時，ψ=5.2，壁厚為3 mm時，ψ=4。

表1單相液體區不同壁厚加熱側與絕熱側熱流量比值

2.3 均勻加熱管內換熱特性及摩擦壓降特性

對管徑φ14*3 mm的均勻加熱管內的換熱系數與壓降進行數值模擬，入口流速范圍為0.5～2.5 m/s，熱流密度為600～2 000 kW/m2，具體參數設置如表2所示。數值模擬結果與經典的傳熱系數公式和摩擦壓降系數公式進行對比，對比結果如圖4-5所示。

Dittus-Boelter傳熱系數計算公式：

摩擦壓降計算公式：

表2數值模擬流體參數表

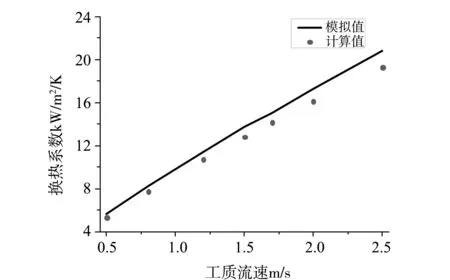
圖4 均勻加熱管內換熱特性

圖5 均勻加熱管內摩擦壓降特性

由圖4-5可以看出，數值模擬結果與經驗關聯式預測結果基本一致，摩擦壓降和換熱系數模擬值與計算值最大誤差分別為2.8%和7.38%，說明所采用的數值方法是正確的。

2.4 非均勻加熱管內換熱特性及摩擦壓降特性

為與均勻加熱管內的換熱特性和摩擦阻力特性進行對比，采用相同的圓管尺寸φ14*3 mm，相同的入口流速0.5～2.5 m/s，加熱側熱流密度同樣為600～2 000 kW/m2，絕熱側熱流密度為0。具體的參數設置如表2所示。將非均勻加熱管內平均換熱系數和摩擦壓降與均勻加熱時的模擬值進行對比。對比結果如圖6-7所示。非均勻加熱管內平均換熱系數和摩擦壓降與均勻加熱時相比最大偏差分別為7.68%和4.8%，說明在所計算的參數范圍內，管外熱負荷非均勻分布對管內單相流的平均換熱系數和摩擦壓降影響不大，可以采用均勻加熱管內的相應計算關聯式進行預測。這與Lekakh[6]和Dedov[7]的研究結論一致。

圖7 非均勻加熱管內摩擦壓降特性

圖6 非均勻加熱管內換熱特性

對加熱側和絕熱側的換熱系數進行了對比計算，對比結果如圖8所示。由圖8可以看出加熱側和絕熱側換熱系數差別較大，絕熱側換熱系數比加熱側換熱系數大，而且工質流速越大，管內換熱越好，兩者差別越大。

圖8 加熱側與絕熱側換熱系數對比

3 結束語

針對螺旋管半周加熱的特點，在課題研究的參數范圍下，采用FLUENT對半周加熱在不同熱流密度、不同管內工質流速不同壁厚的壁溫分布及加熱側與絕熱側的熱流量比值進行了計算。結果表明：熱流密度一定時，管內工質流速越高，兩側熱流量比值越大，不均勻程度越強；管內工質流速相同時，熱流密度對不均度的影響不是很大。壁厚越小，兩側不均勻度越大。

分析了非均勻加熱對管內換熱特性和摩擦阻力特性的影響，對比結果表明管外熱負荷非均勻分布對管內單相流的平均換熱系數和摩擦壓降影響不大，可以采用均勻加熱管內的相應計算關聯式進行預測。加熱側和絕熱側換熱系數差別較大，絕熱側換熱系數比加熱側換熱系數大，而且工質流速越大，管內換熱越好，兩者差別越大。