十進(jìn)制整數(shù)編碼的DE算法模式集定理研究

王凱光,高岳林

(北方民族大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,寧夏 銀川750021)

1.引言和預(yù)備知識

差分進(jìn)化算法(Differential Eveolution,簡稱DE[1?3])是由Storn和Price于1995年提出的為解決切比雪夫不等式(Chebyshev Inequality)的一種采用浮點(diǎn)矢量編碼的在連續(xù)空間進(jìn)行搜索的全局優(yōu)化算法[4?6],是通過差分方式進(jìn)行迭代搜索的全局性進(jìn)化算法,具有簡單、易實(shí)現(xiàn)、收斂性好、魯棒性強(qiáng)等優(yōu)點(diǎn)[7?13],但就算法尋優(yōu)的本質(zhì)上說,其大小如何影響種群多樣性的分布,進(jìn)而影響算法的收斂性質(zhì)[11,13],在理論機(jī)制上面尚未得到說明.鑒于此,本文將在二進(jìn)制模式定理[14?15]研究基礎(chǔ)上,應(yīng)用十進(jìn)制編碼對DE算法的動力學(xué)機(jī)制進(jìn)行初步研究,探索種群規(guī)模(NP)、收縮因子(F)、交叉概率(CR) 等控制參數(shù)對種群尋優(yōu)的動力學(xué)機(jī)制,并提出相應(yīng)的編碼規(guī)則以及基本概念,給出能夠很好解釋DE算法各類參數(shù)對種群尋優(yōu)能力影響的十進(jìn)制模式集定理.

ⅠDE算法原理

一般地,極小化優(yōu)化問題如下表示:

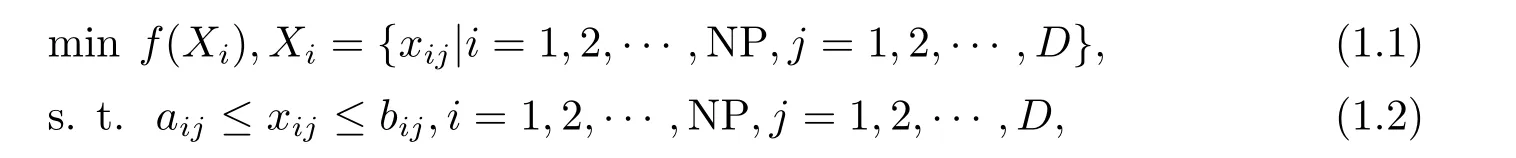
其中,D為決策變量的維數(shù),NP為種群規(guī)模,f(Xi)為適應(yīng)度函數(shù),Xi(i=1,2,··· ,NP) 為D維參量矢量,xij(i= 1,2,··· ,NP;j= 1,2,··· ,D)為第i個個體的第j個分量,aij,bij分別為尋優(yōu)范圍的下界和上界,差分進(jìn)化算法(Differential Eveolution,DE)基本操作原理如下描述[1,4,7].

(i)初始化種群

設(shè)置DE算法的種群為X(t),則個體可表示為:

其中t為進(jìn)化代數(shù),NP為種群規(guī)模.

初始化種群:確定所求優(yōu)化問題的維數(shù)D,最大進(jìn)化代數(shù)T,種群規(guī)模NP,設(shè)置生成初值尋優(yōu)向量如下所示:

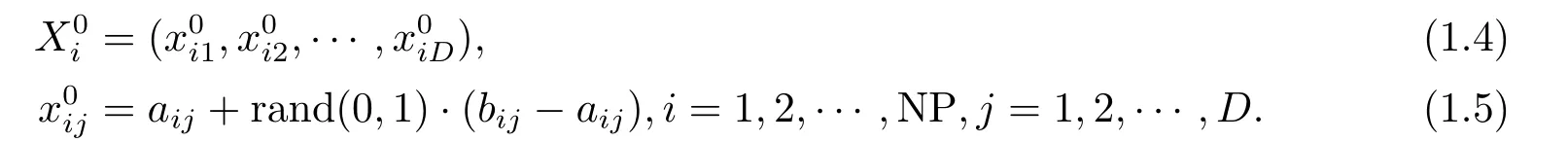
(ii)變異操作

DE算法的個體變異成分是父代個體的差分矢量,每次差分變異個體均來源于第t代父代個體種群中的兩個個體(Xti1,Xti2),其……