馬爾科夫與ARIMA組合模型對地區降雨量的預測研究

徐夢茹 王學明

1(寧夏大學信息工程學院 寧夏 銀川 750001)2(寧夏大學網絡信息管理中心 寧夏 銀川 750001)

0 引 言

年降雨量與地區農作物收成、交通出行等方面息息相關。降雨量的多少將直接影響地區經濟發展，尤其是農業方面的發展，降雨量太多或太少都會造成農作物的歉收；降雨量的多少也會影響流域水資源的豐富程度。若能夠將年降雨量準確預測出來，這將對防洪抗洪、農業生產工作起到非常大的積極作用。但因為地理位置的差異，各個地方對于降雨量的預測需要因地而異。本文根據某地區從1949年到2017年的年降雨量歷史數據對2018年的年降雨量數值作出預測，通過此次實驗為準確預報年降雨量提供合理的依據。降雨量預測流程如圖1所示。

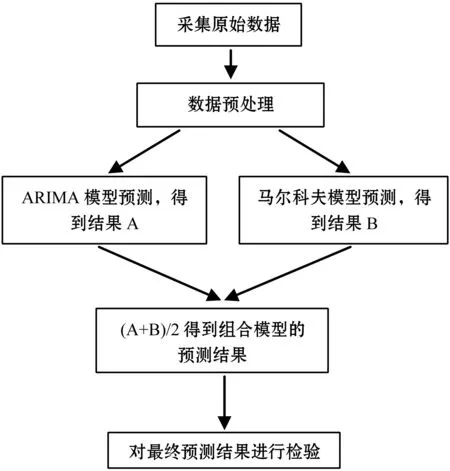
圖1 降雨量預測流程

1 馬爾科夫模型

一般要預測事物發展的趨勢，必須要知道此事物歷史情況與當前情況，并加以綜合考慮，同時有相當一部分的預測方法需要知道預測事物的歷史及當下數據，才能進行建模，并應用于實際生活中。但馬爾科夫模型則認為只要知道當前的狀態，便可以預測未來的情況，不需要知道事物發展的歷史狀態。這種性質稱為馬爾科夫性[1-2]。馬爾科夫模型是根據系統狀態之間的轉移概率來預測系統的未來發展。

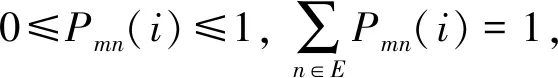
定義2將轉移頻數矩陣的第j列之和除以所有轉移頻數之和，所得值為邊際概率，記為P·j，即有：

(1)

當n充分大時，統計量服從自由度為(m-1)2的X2分布。其公式如下：

(2)

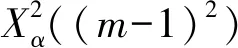
定義3數據序列是相依的隨機變量，采用自相關系數作為相依關系強弱的度量，第s步的自相關系數為：

(3)

(4)

式中：ωs為第s步的馬爾科夫權重;l為最大轉移步數。

2 ARIMA模型

ARIMA模型的基本思想是將預測對象隨時間推移而形成的數據序列視為一個隨機序列，用一定的數學模型來近似描述這個序列。它的具體形式可以表達成ARIMA(p,d,q)，其中：p表示自回歸過程的階數；d表示查分階數；q表示移動平均過程的階數[3-4]。ARIMA模型建模過程及具體步驟如圖2所示。

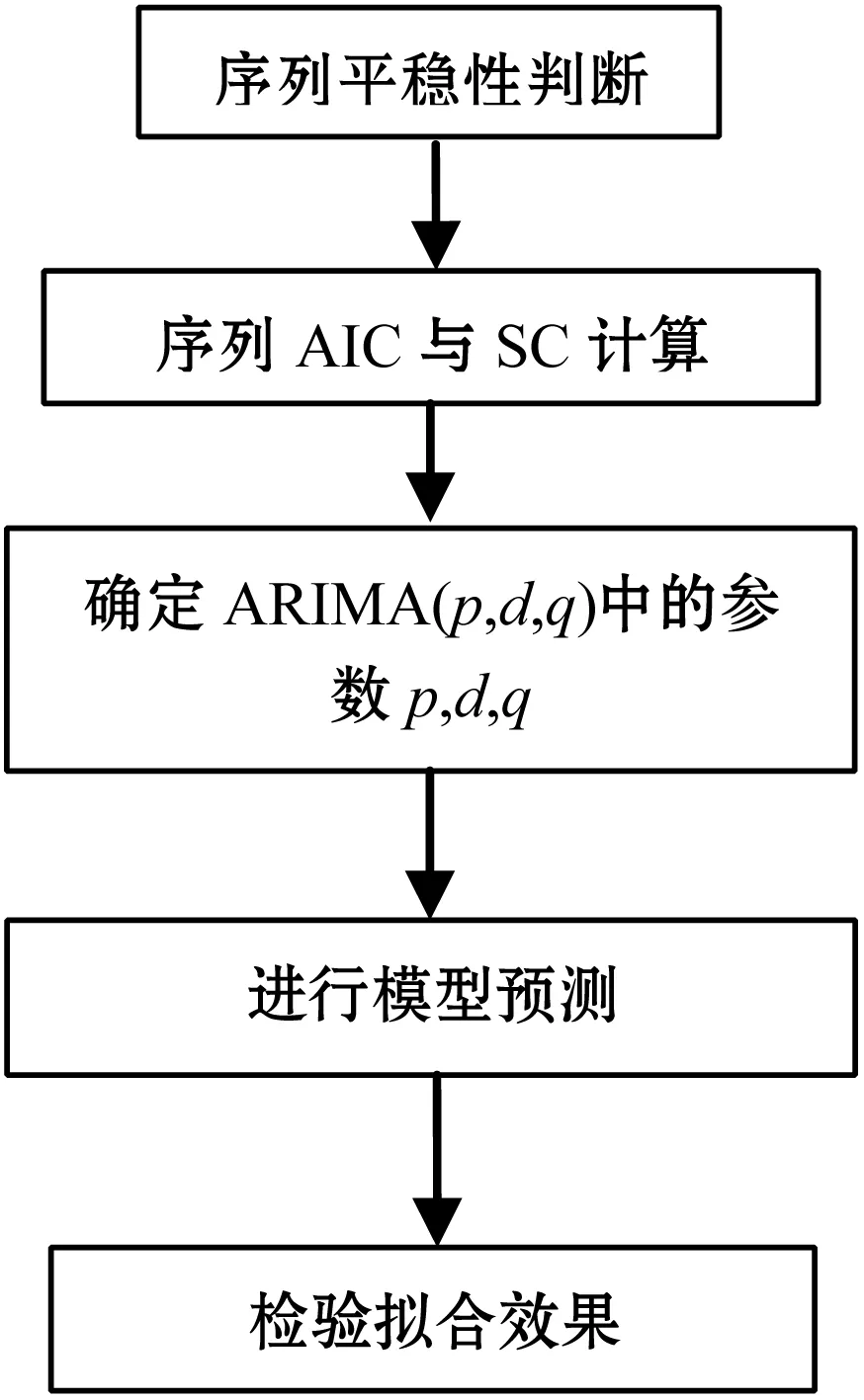
圖2 ARIMA模型預測流程

3 實驗過程及結果

實驗選取的原始數據為某地區1949年-2017年的年降雨量數據。其中，將1949年-2014年數據作為模型訓練集，2015年-2017年數據作為模型測試集，所有預測過程均用MATLAB與R語言完成。

3.1 ARIMA模型預測

(1) 序列平穩性判斷。根據降雨量數據做出時序圖，如圖3所示。

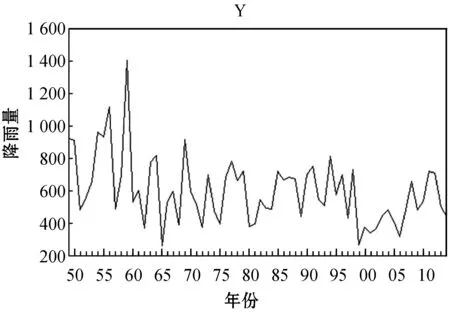
圖3 序列時序圖

根據時序圖可知原數據接近平穩，之后用ADF單位根檢驗法來進行檢驗，通過計算得出Dickey-Fuller=-6.662 674，概率P=0.000 0<0.05，說明序列平穩，不用進行差分平穩化數據，故ARIMA(p,d,q)中d=0。

(2) 模型識別。根據數據得出自相關圖與偏自相關圖，如圖4、圖5所示。

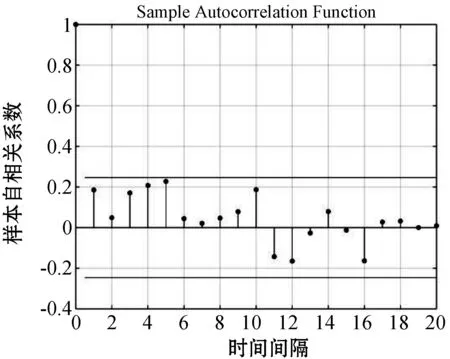
圖4 自相關圖

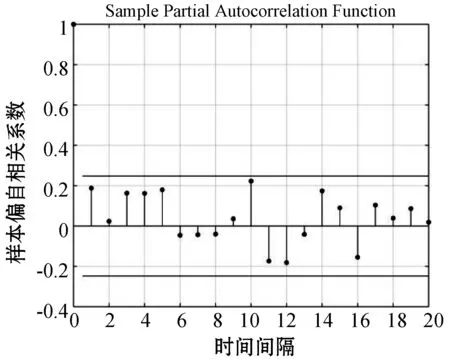
圖5 偏自相關圖

選取部分(p,q)來進行AIC驗證，得到各模型檢驗結果，如表1所示。

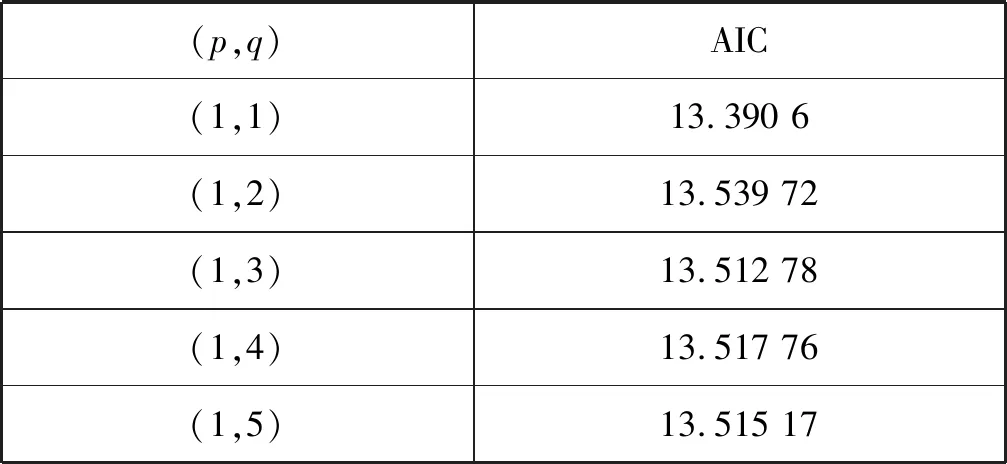
表1 模型檢驗結果

從表1中可知,當(p,q)=(1,1)時AIC 的值最小，理應選擇p=1、q=1，但經過后期誤差分析可知，當p=1、q=5時誤差最小，即預測最準確，所以本實驗中的ARIMA模型選用ARIMA(1,0,5)[5]。

(3) 模型預測。經過預測，得到2015年的降雨量預測值為565.894 8 mm，2016年的降雨量預測值為614.572 6 mm，2017年降雨量預測值為611.973 6 mm，平均相對誤差為3.94%，預測結果較好。并將其應用于2018年降雨量預測，得到預測值為579.165 1 mm。

3.2 馬爾科夫模型預測

(1) 馬氏性檢驗。根據規定，一般情況下，當年降雨量t小于平均降雨量的-25%為枯水年，小于-10%偏枯年，-10%～10%為平水年，大于10%為偏豐年，大于25%為豐水年[6]。由此可以將降雨量劃分為5個等級，如表2所示。

表2 降雨量等級狀態劃分

由此得到：

各步轉移概率為：

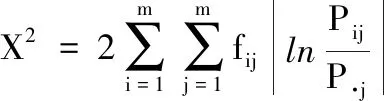
表3 統計量計算表

(2) 預測過程:

① 計算各階自相關系數及權重。由式(3)求得序列各階自相關系數r=(0.186,0.049,0.171,0.208,0.228)，再由式(4)得權重向量為ω=(0.206 2,0.054 3,0.189 6,0.230 6,0.252 8)。

② 根據1949年-2014年的歷史降雨量數據分別預測2015年-2017年降雨量數據。以2015年為例，如表4所示。

表4 2015年降水量預測狀態

由表4可知，將同一概率加權后的最大值為0.290 7，即2015年的預測狀態為1，同理可得2016年、2017年預測狀態分別為3和3，同時求得2015年到2017年的預測降雨量分別為499.33 mm、599.1 mm、599.1 mm。實際上2015年到2017年的降水狀態都為3，得出平均相對誤差為10.17%。

最后根據實際2013年到2017年降水量數據，得到2018年預測的狀態為2，降水量預測為519.26 mm。

3.3 兩種模型組合預測

通常，ARIMA模型較為簡單，只需要內生變量而不需要借助其他外生變量，但是其本質上只能用來預測線性關系，不能預測非線性關系[7]。馬爾可夫模型不適合用于系統中長期數據的預測，理論上只能用于預測短期內的數據[8]。基于對以上兩種模型的分析，本文將ARIMA模型得到的預測結果與馬爾科夫模型的預測結果進行求平均值的操作，見表5。

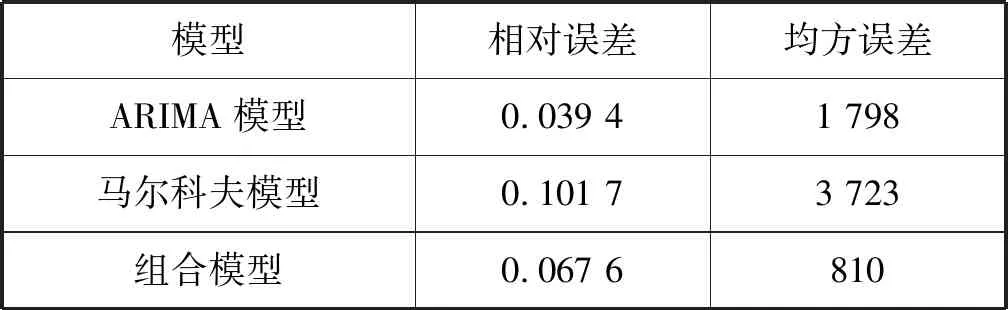
表5 預測模型誤差對比

在相對誤差相差不大的情況下，組合模型的均方誤差相較ARIMA模型和馬爾科夫模型的均方誤差明顯下降，說明組合模型預測的穩定性較高，此組合模型有較高的應用價值。

4 結 語

本文通過將兩種模型組合對地區降雨量進行預測，所達到的預測結果較好。基于目前降雨量預測模型，本文所提出的組合模型還有一些地方需要進一步改進，以提高預測準確度和穩定性。預測準確度的提高將有利于相關部門制定相關的方案措施來應對不同的降雨量帶來的后果，做到防患于未然。