基于OBDD訪問(wèn)結(jié)構(gòu)的無(wú)配對(duì)CP-ABE方案

丁晟，曹進(jìn)，李暉

（西安電子科技大學(xué)網(wǎng)絡(luò)與信息安全學(xué)院，陜西 西安 710071）

1 引言

物聯(lián)網(wǎng)作為傳統(tǒng)互聯(lián)網(wǎng)的延伸，旨在將現(xiàn)存的互聯(lián)網(wǎng)與人們生活中的各種智能設(shè)備緊密結(jié)合，徹底打破數(shù)據(jù)孤島，讓數(shù)據(jù)流動(dòng)起來(lái)。通過(guò)將數(shù)十億的智能設(shè)備互聯(lián)，物聯(lián)網(wǎng)給予了智能電網(wǎng)、智慧城市、智能家居、智慧醫(yī)療等新模式更多的可能。然而，隨著物聯(lián)網(wǎng)設(shè)備之間的關(guān)系越來(lái)越緊密，如何保證數(shù)據(jù)在物聯(lián)網(wǎng)中安全高效的共享成為一個(gè)相當(dāng)棘手的問(wèn)題。當(dāng)物聯(lián)網(wǎng)智能設(shè)備之間共享數(shù)據(jù)時(shí)，潛在的安全問(wèn)題如數(shù)據(jù)泄露、數(shù)據(jù)完整性被破壞或未授權(quán)訪問(wèn)等都將嚴(yán)重影響數(shù)據(jù)在共享過(guò)程中的安全。

隨著物聯(lián)網(wǎng)設(shè)備數(shù)量的急劇增長(zhǎng)，數(shù)據(jù)量規(guī)模也日趨龐大，單純依靠設(shè)備自身存儲(chǔ)和處理數(shù)據(jù)極易使其淹沒(méi)在海量的數(shù)據(jù)之下。云計(jì)算作為互聯(lián)網(wǎng)技術(shù)另一重要革新，其豐富的存儲(chǔ)和計(jì)算資源可幫助物聯(lián)網(wǎng)設(shè)備代理存儲(chǔ)和處理數(shù)據(jù)。物聯(lián)網(wǎng)設(shè)備可將本地存儲(chǔ)的數(shù)據(jù)上傳至云端，并可隨時(shí)從云端下載數(shù)據(jù)，以節(jié)省本地存儲(chǔ)資源。對(duì)于那些難以處理的數(shù)據(jù)，由于物聯(lián)網(wǎng)設(shè)備自身計(jì)算資源有限，可以將數(shù)據(jù)提交給云端，利用云計(jì)算豐富的計(jì)算資源對(duì)數(shù)據(jù)進(jìn)行必要的處理后，直接使用云計(jì)算返回的結(jié)果來(lái)進(jìn)行下一步?jīng)Q策。

由于數(shù)據(jù)存儲(chǔ)在云端，脫離了數(shù)據(jù)所有者的直接管控，其安全性將受到極大挑戰(zhàn)。針對(duì)這一問(wèn)題，普遍的解決方案是將數(shù)據(jù)加密，以密文形式存儲(chǔ)在云端。基于屬性的加密能同時(shí)實(shí)施數(shù)據(jù)加密和訪問(wèn)控制，有效保證了數(shù)據(jù)在共享過(guò)程中的安全。然而，直接將基于屬性的加密應(yīng)用到物聯(lián)網(wǎng)設(shè)備上還存在一些問(wèn)題，如其一直被詬病的效率問(wèn)題。傳統(tǒng)的基于屬性加密的方案構(gòu)造中都涉及雙線性配對(duì)這一運(yùn)算，經(jīng)實(shí)驗(yàn)測(cè)試，一次雙線性配對(duì)的計(jì)算開(kāi)銷大約是同一橢圓曲線下一次標(biāo)量乘法運(yùn)算的2～3倍[1]。因此，盡可能減少算法中雙線性配對(duì)的計(jì)算次數(shù)，或者巧妙運(yùn)用其他運(yùn)算實(shí)現(xiàn)同樣的算法功能，可在一定程度上提高基于屬性加密的算法效率。

訪問(wèn)結(jié)構(gòu)的設(shè)計(jì)也是基于屬性加密中相當(dāng)重要的一環(huán)。訪問(wèn)結(jié)構(gòu)具有多種表現(xiàn)形式，例如線性秘密分享方案（LSSS,linear secret sharing scheme）[2]、與門[3]、門限[4]等。訪問(wèn)結(jié)構(gòu)的優(yōu)化可以提升密文策略屬性基加密（CP-ABE,ciphertext-policy attribute-based encryption）系統(tǒng)的運(yùn)行效率，可以提高訪問(wèn)策略的可表達(dá)能力，還能通過(guò)減少策略中冗余的屬性來(lái)縮小密文長(zhǎng)度。

本文基于有序二元決策圖（OBDD,ordered binary decision diagram）訪問(wèn)結(jié)構(gòu)，為物聯(lián)網(wǎng)系統(tǒng)提出了一種新的無(wú)配對(duì)基于屬性的加密方案，主要貢獻(xiàn)如下。

1)為物聯(lián)網(wǎng)系統(tǒng)提出了一種新的無(wú)配對(duì)基于屬性的加密方案。該方案對(duì)傳統(tǒng)CP-ABE進(jìn)行了相關(guān)改進(jìn)，利用橢圓曲線上較為輕量級(jí)的標(biāo)量乘法代替復(fù)雜的雙線性配對(duì)運(yùn)算，有效降低了方案的計(jì)算開(kāi)銷。

2)基于OBDD技術(shù)優(yōu)化了訪問(wèn)策略的數(shù)據(jù)結(jié)構(gòu)，不僅支持任意關(guān)于屬性的布爾表達(dá)式，還同時(shí)支持訪問(wèn)策略中屬性的正負(fù)值。

2 相關(guān)研究

在過(guò)去的十年中，雙線性配對(duì)的出現(xiàn)解決了許多之前在密碼學(xué)領(lǐng)域無(wú)法解決的問(wèn)題[5-7]。基于雙線性配對(duì)，ABE被提出用于實(shí)現(xiàn)數(shù)據(jù)加密和訪問(wèn)控制的結(jié)合。Bethencourt等[4]提出了CP-ABE的具體構(gòu)造，在他們的方案設(shè)計(jì)中，加密算法基于數(shù)據(jù)擁有者建立的訪問(wèn)樹(shù)來(lái)加密消息。每個(gè)用戶擁有一組代表其身份的屬性以及每個(gè)屬性對(duì)應(yīng)的屬性密鑰。解密算法利用拉格朗日插值法來(lái)解密密文。Waters[2]基于LSSS訪問(wèn)結(jié)構(gòu)提出了一個(gè)較為靈活的CP-ABE構(gòu)造，并基于該構(gòu)造提出了新的方案，改善了原有方案的不足。

2007 年，Cheung 等[3]提出了一種支持與門訪問(wèn)結(jié)構(gòu)的CP-ABE 方案，該方案同時(shí)支持正負(fù)2種屬性。Zhou等[8]提出了一種密文長(zhǎng)度恒定的CP-ABE方案，密文長(zhǎng)度不隨系統(tǒng)中屬性數(shù)量的變化而變化。該方案性能良好，但不支持非單調(diào)或析取范式的訪問(wèn)結(jié)構(gòu)。Wang等[9]解決了CP-ABE 方案中的密鑰托管問(wèn)題，同時(shí)提高了屬性的可表達(dá)性。Guo等[10]提出了一種密鑰長(zhǎng)度恒定的CP-ABE方案，該方案中解密密鑰的數(shù)量獨(dú)立于屬性的數(shù)量。Li等[11]基于OBDD訪問(wèn)結(jié)構(gòu)提出了一種新型的CP-ABE方案，該方案充分利用了OBDD訪問(wèn)結(jié)構(gòu)豐富的表達(dá)性和計(jì)算上的高效性，但方案仍涉及雙線性對(duì)的運(yùn)算。盡管CP-ABE方案能有效保證云中數(shù)據(jù)的安全，并實(shí)施細(xì)粒度的訪問(wèn)控制，但方案中涉及大量雙線性配對(duì)運(yùn)算和模冪運(yùn)算，計(jì)算開(kāi)銷過(guò)大這一問(wèn)題嚴(yán)重限制了將其應(yīng)用于物聯(lián)網(wǎng)中的資源受限型的設(shè)備。

眾所周知，基于配對(duì)的密碼學(xué)協(xié)議的計(jì)算效率取決于配對(duì)運(yùn)算的計(jì)算速度。針對(duì)這一問(wèn)題，學(xué)者們進(jìn)行了大量的研究[12-16]。為了優(yōu)化橢圓曲線密碼（ECC,elliptic curve cryptography）協(xié)議，F(xiàn)reeman等[17]分類列舉了一些對(duì)于配對(duì)運(yùn)算友好的橢圓曲線，并介紹了它們的具體構(gòu)造以及相關(guān)的一些優(yōu)化技術(shù)。Scott[18]分析了如何選擇配對(duì)類型及橢圓曲線以提高ABE方案的計(jì)算效率。Rivain[19]詳細(xì)討論了如何在ECC方案中更快地計(jì)算標(biāo)量乘法。

一種降低用戶計(jì)算開(kāi)銷的方法是將復(fù)雜的運(yùn)算外包給其他具有更強(qiáng)計(jì)算能力的實(shí)體。Chevallier-Mames等[20]在單不可信服務(wù)器模型下提出了一種將復(fù)雜的雙線性配對(duì)計(jì)算外包的方案，但與Chen等[21]所提方案相比，計(jì)算開(kāi)銷仍較高。Chen等在雙不可信服務(wù)器?單惡意實(shí)體模型下提出了一種新的計(jì)算外包算法，該算法計(jì)算效率更高，但其安全模型在實(shí)際應(yīng)用中是不現(xiàn)實(shí)的。

一種較為直接的方法是將部分解密工作外包給云端。2011年，Green等[22]提出了一種解密外包的ABE 方案，屬性私鑰由兩部分組成：El Gamal密鑰和轉(zhuǎn)換密鑰。代理方可以利用轉(zhuǎn)換密鑰對(duì)密文進(jìn)行部分解密，部分解密的結(jié)果為簡(jiǎn)單的El Gamal密文，用戶只需再利用El Gamal 密鑰進(jìn)行簡(jiǎn)單運(yùn)算即可完成解密。Li等[23]對(duì)這種方式進(jìn)行了改進(jìn)，使其同時(shí)支持對(duì)密鑰分發(fā)和解密的外包。然而，這種計(jì)算外包方式只是將計(jì)算開(kāi)銷轉(zhuǎn)移到了代理方或云服務(wù)器，對(duì)于整個(gè)系統(tǒng)來(lái)說(shuō)，計(jì)算開(kāi)銷并沒(méi)有得到有效降低。

為了從根本上優(yōu)化ABE算法，本文利用其他更高效的算術(shù)運(yùn)算代替復(fù)雜的雙線性對(duì)運(yùn)算。Odelu等[24]基于橢圓曲線密碼學(xué)提出了一種密鑰長(zhǎng)度恒定的CP-ABE方案，但該方案只支持與門訪問(wèn)結(jié)構(gòu)，限制了方案的靈活性。隨后，他們基于RSA提出了一種新的密鑰長(zhǎng)度和密文長(zhǎng)度均恒定的CP-ABE方案[25]。雖然該方案加密和解密的時(shí)間復(fù)雜度均為O(1)，但仍只支持與門訪問(wèn)結(jié)構(gòu)。

3 基礎(chǔ)知識(shí)

3.1 有序二元決策圖

二元決策圖（BDD）是一個(gè)有根、有向的非循環(huán)圖，可用于高效的表示布爾函數(shù)。所有的布爾函數(shù)都可以轉(zhuǎn)換為變量之間基本邏輯運(yùn)算，例如AND、OR、NOT等的組合。

BDD由2種節(jié)點(diǎn)構(gòu)成：決策節(jié)點(diǎn)和終端節(jié)點(diǎn)。每個(gè)決策節(jié)點(diǎn)會(huì)被標(biāo)記為某一布爾變量，同時(shí)決策節(jié)點(diǎn)擁有2個(gè)子節(jié)點(diǎn)。當(dāng)布爾變量獲得賦值為1時(shí)，它的子節(jié)點(diǎn)被稱為高節(jié)點(diǎn)；當(dāng)獲得賦值為0時(shí)，它的子節(jié)點(diǎn)被稱為低節(jié)點(diǎn)。如果二元決策圖中所有路徑上的不同變量從根節(jié)點(diǎn)開(kāi)始都以同樣的次序出現(xiàn)，那么這種二元決策圖被稱為有序二元決策圖（OBDD）。

舉例來(lái)說(shuō)，圖1是用OBDD表示布爾函數(shù)f(x0,x1,x2,x3)=x0+x1x2+x1x3+x2x3。決策節(jié)點(diǎn)用圓圈表示，終端節(jié)點(diǎn)用方塊表示。實(shí)線表示通向高節(jié)點(diǎn)的邊，虛線表示通向低節(jié)點(diǎn)的邊。布爾函數(shù)f(x0,x1,x2,x3)=x0+x1x2+x1x3+x2x3的值是通過(guò)從根節(jié)點(diǎn)開(kāi)始沿著決策圖中的某一路徑向下，依次為每個(gè)決策節(jié)點(diǎn)中的變量賦值來(lái)得到的。函數(shù)f(x0=1,x1=1,x2=0,x3=0)的值可以從x0開(kāi)始，沿實(shí)線向下移動(dòng)到x1，再沿著實(shí)線移動(dòng)到x2，最后連續(xù)沿著2條虛線移動(dòng)到終端節(jié)點(diǎn)1。

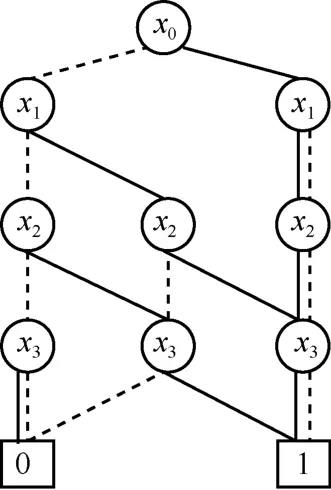
圖1 布爾函數(shù)f(x0,x1,x2,x3)=x0+x1x2+x1x3+x2x3的OBDD表示

3.1.1 生成OBDD訪問(wèn)結(jié)構(gòu)

本節(jié)詳細(xì)介紹如何將一個(gè)布爾表達(dá)式轉(zhuǎn)換成對(duì)應(yīng)的OBDD訪問(wèn)結(jié)構(gòu)。

假設(shè)系統(tǒng)中定義了n種屬性i，編號(hào)依次為i0,i1,…,in-1。訪問(wèn)策略包含系統(tǒng)中定義的所有屬性。屬性i的屬性值為正，代表該訪問(wèn)策略要求滿足策略的屬性集里需含有屬性i；屬性i的屬性值為負(fù)，代表滿足策略的屬性集里不需要含有屬性i。基于布爾表達(dá)式的訪問(wèn)策略可表示為f(i0,i1,…,in-1)。

將OBDD中的所有節(jié)點(diǎn)進(jìn)行編號(hào)，獲得最終訪問(wèn)結(jié)構(gòu)的表達(dá)式為

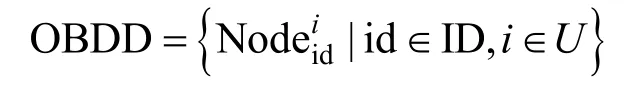
其中，ID是決策節(jié)點(diǎn)序號(hào)的集合；U是訪問(wèn)結(jié)構(gòu)里出現(xiàn)的屬性的集合；是一個(gè)元組(id,i,high,low)，id是當(dāng)前節(jié)點(diǎn)的序號(hào)，i是當(dāng)前節(jié)點(diǎn)內(nèi)屬性的序號(hào)，high代表1分支節(jié)點(diǎn)，low代表0分支節(jié)點(diǎn)，如圖2所示。

3.1.2 判斷是否滿足訪問(wèn)結(jié)構(gòu)

假設(shè)U是一個(gè)屬性集，判斷該屬性集是否滿足訪問(wèn)結(jié)構(gòu)OBDD可按如下方式進(jìn)行。

從根節(jié)點(diǎn)開(kāi)始，對(duì)于具有屬性i的決策節(jié)點(diǎn)，如果該屬性i屬于集合U，則代表該屬性的屬性值為1，判斷過(guò)程將沿1分支節(jié)點(diǎn)向下；否則，判斷將沿0分支節(jié)點(diǎn)向下。以上過(guò)程將重復(fù)執(zhí)行直到抵達(dá)終端節(jié)點(diǎn)。如果終端節(jié)點(diǎn)為1，則表示屬性集U滿足該訪問(wèn)策略O(shè)BDD；如果終端節(jié)點(diǎn)為0，則表示屬性集U不滿足該訪問(wèn)策略O(shè)BDD。

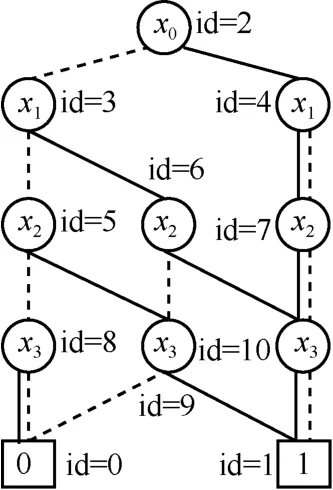
圖2 生成OBDD訪問(wèn)結(jié)構(gòu)

3.2 CP-ABE框架

一個(gè)CP-ABE系統(tǒng)通常由5種算法組成，分別為系統(tǒng)初始化、授權(quán)機(jī)構(gòu)設(shè)置、密鑰生成、加密和解密，定義如下。

系統(tǒng)初始化 (k)→PP

系統(tǒng)設(shè)置算法將安全參數(shù)k作為輸入，然后輸出系統(tǒng)所需的全部公共參數(shù)PP。

授權(quán)機(jī)構(gòu)設(shè)置 (PP)→PK,SK

基于第一步生成的公共參數(shù)PP，屬性授權(quán)機(jī)構(gòu)為自己和系統(tǒng)中的每一個(gè)屬性生成公鑰PK和私鑰SK。

密鑰生成(PP,i,GID,SK)→SKi,GID

密鑰生成算法將公共參數(shù)、屬性i、身份GID以及屬性授權(quán)機(jī)構(gòu)的SK作為輸入，輸出屬性私鑰SKi,GID，并將其發(fā)送給對(duì)應(yīng)的用戶。

加密 (PP,M,(A,ρ),{PKi })→CT

給定一消息M，訪問(wèn)矩陣(A,ρ)和訪問(wèn)策略中所有屬性的公鑰，加密算法輸出密文CT。

解密(PP,CT,{SKi,GID})→M

如果某個(gè)用戶擁有的一組屬性滿足密文的訪問(wèn)策略，解密算法可以成功恢復(fù)消息M，否則解密失敗。

3.3 安全模型

本節(jié)給出無(wú)配對(duì)運(yùn)算的CP-ABE方案的安全模型。該模型由以下描述的挑戰(zhàn)者和敵手之間的游戲定義。

初始化

敵手首先選擇一個(gè)挑戰(zhàn)訪問(wèn)結(jié)構(gòu)A，然后將其發(fā)送給挑戰(zhàn)者。

設(shè)置

挑戰(zhàn)者運(yùn)行設(shè)置算法，為系統(tǒng)生成必要的全局參數(shù)，為每個(gè)屬性生成公私鑰對(duì)。然后挑戰(zhàn)者將系統(tǒng)全局參數(shù)和屬性公鑰發(fā)送給敵手。

階段1

攻擊者可以自適應(yīng)地查詢?nèi)魏螌傩运借€，唯一的限制是相查詢的屬性集不能滿足挑戰(zhàn)訪問(wèn)結(jié)構(gòu)A。

挑戰(zhàn)階段

敵手選擇2條等長(zhǎng)的消息M0和M1，并將它們發(fā)送給挑戰(zhàn)者。然后挑戰(zhàn)者擲一枚隨機(jī)硬幣β∈{0,1}，并在訪問(wèn)結(jié)構(gòu)A下對(duì)消息Mβ加密，然后發(fā)送給敵手。

階段2

敵手可以繼續(xù)查詢屬性私鑰，唯一的限制條件與階段1相同。

猜測(cè)

敵手對(duì)β輸出猜測(cè)結(jié)果β′。敵手在這場(chǎng)游戲中的優(yōu)勢(shì)被定義為

定義1如果任何多項(xiàng)式時(shí)間敵手贏得這個(gè)安全游戲的優(yōu)勢(shì)是可以被忽略的，則所提方案被認(rèn)為是選擇性CPA安全的。

3.4 DDH假設(shè)

橢圓曲線上的判定性Diffie-Hellman（DDH,decisional Diffie-Hellman）假設(shè)的定義描述如下。

挑戰(zhàn)者選擇一個(gè)素?cái)?shù)階r的循環(huán)群P。令G是循環(huán)群P的一個(gè)生成元，a和b是從Zr中隨機(jī)選擇的。如果挑戰(zhàn)者給攻擊者一個(gè)元組(G,aG,bG)，那么攻擊者在多項(xiàng)式時(shí)間內(nèi)區(qū)分元素abG∈P和隨機(jī)元素R∈P是困難的。算法β解決P中DDH假設(shè)的優(yōu)勢(shì)定義為ε，當(dāng)

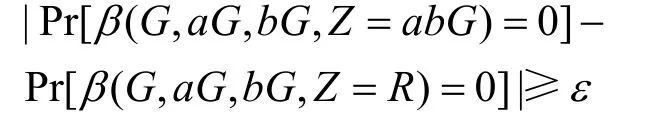
定義2如果多項(xiàng)式時(shí)間算法解決DDH困難問(wèn)題的優(yōu)勢(shì)是可忽略的，那么DDH假設(shè)是成立的。

4 方案構(gòu)造

本節(jié)將給出為物聯(lián)網(wǎng)中高效安全數(shù)據(jù)共享所設(shè)計(jì)的基于OBDD訪問(wèn)結(jié)構(gòu)的無(wú)配對(duì)CP-ABE的具體構(gòu)造。由于雙線性配對(duì)一直被認(rèn)為是基于屬性加密方案設(shè)計(jì)中計(jì)算開(kāi)銷最大的運(yùn)算，因此本文選擇用橢圓曲線上相對(duì)輕量級(jí)的標(biāo)量乘法來(lái)代替復(fù)雜的雙線性配對(duì)運(yùn)算，以提高方案在加密和解密階段的計(jì)算效率。此外，采用基于OBDD的訪問(wèn)結(jié)構(gòu)來(lái)提高訪問(wèn)策略的表達(dá)能力，該類型訪問(wèn)結(jié)構(gòu)既同時(shí)支持屬性的正負(fù)值，也支持任何布爾運(yùn)算。所提方案由以下5種算法組成。

1)系統(tǒng)初始化

令GF(p)為一階為p的有限域。E是定義在GF(p)上的一條橢圓曲線。G是橢圓曲線E上一階為r的元素。G生成了一個(gè)E的循環(huán)子群，其中橢圓曲線離散對(duì)數(shù)問(wèn)題是困難的。

2)授權(quán)機(jī)構(gòu)設(shè)置

3)密鑰生成

假設(shè)用戶擁有一屬性集U。對(duì)于系統(tǒng)中定義的每一個(gè)屬性i，如果i∈U，那么對(duì)于該用戶來(lái)說(shuō)該屬性取正值，對(duì)應(yīng)的屬性私鑰為ki；否則，該屬性取負(fù)值，對(duì)應(yīng)的屬性私鑰為。若為擁有屬性集U的用戶生成密鑰，屬性授權(quán)機(jī)構(gòu)可計(jì)算其中，表示ki或

4)加密

首先，將明文消息映射到橢圓曲線E上的一點(diǎn)M。數(shù)據(jù)擁有者設(shè)置的訪問(wèn)結(jié)構(gòu)為

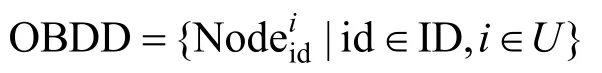
令有效路徑(root→1)的數(shù)量為V，其中每條有效路徑為{Pj,j∈[0,v-1]}。數(shù)據(jù)所有者隨機(jī)選擇s∈Zr，并計(jì)算

整個(gè)密文為{OBDD,C,,j∈[0,V-1]}。

5)解密

若要解密密文CT，數(shù)據(jù)使用者擁有的屬性集必須滿足數(shù)據(jù)擁有者制定的訪問(wèn)策略。具體的解密步驟可以通過(guò)以下遞歸算法實(shí)現(xiàn)。

步驟1尋找編號(hào)為2的節(jié)點(diǎn)，即根節(jié)點(diǎn)，并將其定義為當(dāng)前節(jié)點(diǎn)。

步驟2提取當(dāng)前節(jié)點(diǎn)中包含的信息對(duì)于屬性i：如果，則算法轉(zhuǎn)到步驟3繼續(xù)執(zhí)行；如果表示NOTi），則算法轉(zhuǎn)到步驟4繼續(xù)執(zhí)行。

步驟3搜索當(dāng)前節(jié)點(diǎn)的1分支節(jié)點(diǎn)。

①如果1分支節(jié)點(diǎn)是終端節(jié)點(diǎn)0，則終止遞歸算法并返回解密失敗。

② 如果1分支節(jié)點(diǎn)是終端節(jié)點(diǎn)1，則算法轉(zhuǎn)到步驟5繼續(xù)執(zhí)行。

③如果1分支節(jié)點(diǎn)是非終端節(jié)點(diǎn)，則將其定義為當(dāng)前節(jié)點(diǎn)，算法轉(zhuǎn)到步驟2繼續(xù)執(zhí)行。

步驟4搜索當(dāng)前節(jié)點(diǎn)的0分支節(jié)點(diǎn)。

①如果0分支節(jié)點(diǎn)是終端節(jié)點(diǎn)0，則終止遞歸算法并返回解密失敗。

② 如果0分支節(jié)點(diǎn)是終端節(jié)點(diǎn)1，則算法轉(zhuǎn)到步驟5繼續(xù)執(zhí)行。

③如果0分支節(jié)點(diǎn)是非終端節(jié)點(diǎn)，則將其定義為當(dāng)前節(jié)點(diǎn)，算法轉(zhuǎn)到步驟2繼續(xù)執(zhí)行。

步驟5如若數(shù)據(jù)使用者擁有的屬性集滿足某一條有效路徑Pj，那么為了恢復(fù)出明文M可以計(jì)算

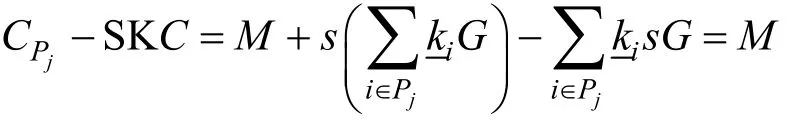
最后，數(shù)據(jù)使用者可以將M映射回明文消息。

5 安全性分析

5.1 安全證明

本節(jié)將證明所提方案在DDH假設(shè)下是選擇性CPA安全的。

定義3如果存在一個(gè)多項(xiàng)式時(shí)間的敵手A可以一個(gè)不可忽略的優(yōu)勢(shì)ε>0來(lái)破解提出的方案，那么存在一個(gè)多項(xiàng)式時(shí)間算法B可以的優(yōu)勢(shì)來(lái)區(qū)分DDH元組和隨機(jī)元組。

令G為E的一個(gè)階為r的生成元，β是集合{0,1}中的隨機(jī)元素，R是E中一隨機(jī)元素。DDH挑戰(zhàn)者C首先隨機(jī)選擇a,b∈Zr。如果β=0，則令Z=abG；否則令Z=R。挑戰(zhàn)者C將元組(G,aG,bG,Z)提交給模擬器B。然后B在下面的游戲中代替C扮演挑戰(zhàn)者的角色。

系統(tǒng)初始化

A首先向B提交一個(gè)挑戰(zhàn)訪問(wèn)結(jié)構(gòu)

設(shè)置

為了給敵手A生成系統(tǒng)中的每個(gè)屬性i的屬性公鑰，B隨機(jī)選擇。令ikaG為正屬性i的公鑰，為負(fù)屬性i的公鑰。因?yàn)槭请S機(jī)選擇的，所以公共參數(shù)實(shí)際上也是隨機(jī)的。

階段1

A自適應(yīng)地將屬性集提交給B以求獲得相應(yīng)的屬性私鑰。唯一限制條件是敵手無(wú)法查詢?nèi)魏慰捎糜诔晒饷苊芪牡膶傩运借€。換句話說(shuō)，屬性集U不能是A的任何有效路徑。

挑戰(zhàn)

A在隨機(jī)選擇2條等長(zhǎng)消息M0,M1∈E，并將它們提交給B。然后B擲一枚隨機(jī)硬幣β∈{0,1}，并根據(jù)訪問(wèn)結(jié)構(gòu)A加密Mβ。令C=bG,B將挑戰(zhàn)密文返回給敵手A。

階段2

與階段1相同。敵手A可以提交其他屬性私鑰查詢，只要不違反與階段1相同的限制條件。

猜測(cè)

A輸出對(duì)β的猜測(cè)β′。如果β′=β，B輸出0表示Z=abG；否則，B輸出1表示Z=R。

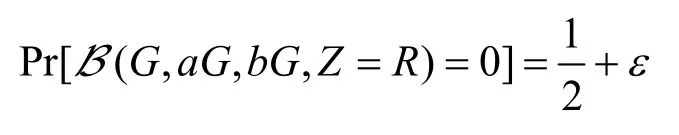
如果Z=R，則對(duì)敵手A而言是完全隨機(jī)的。從而有

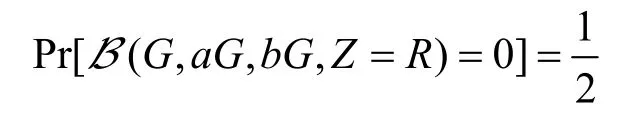
因此，B破解DDH問(wèn)題的優(yōu)勢(shì)為

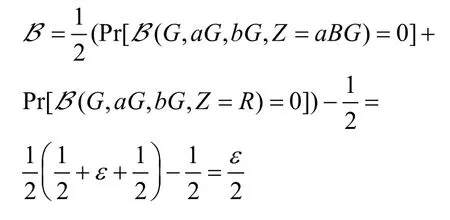
5.2 共謀攻擊

對(duì)于CP-ABE來(lái)說(shuō)，共謀攻擊是方案設(shè)計(jì)時(shí)需要考慮的最重要的安全問(wèn)題之一。由于ABE旨在授予屬性集滿足訪問(wèn)結(jié)構(gòu)的用戶訪問(wèn)權(quán)限，因此不具備訪問(wèn)資格的用戶不應(yīng)能夠恢復(fù)出明文，即使他們彼此串通。換句話說(shuō)，他們不能通過(guò)組合或計(jì)算他們自己的屬性私鑰來(lái)獲得可用于成功解密密文的密鑰。在本文的方案中，每個(gè)用戶的密鑰是其屬性集中每個(gè)屬性值對(duì)應(yīng)的的總和。假設(shè)有n個(gè)屬性，編號(hào)依次為{0,1,2,…,n-1}，每個(gè)屬性對(duì)應(yīng)的密鑰為（當(dāng)屬性值為正時(shí)，屬性私鑰為；否則，）。總共有2n個(gè)可能的密鑰，分別為

實(shí)際上，這2n個(gè)屬性私鑰形成了一個(gè)擁有2n個(gè)變量的線性方程組，分別為

該線性方程組的系數(shù)矩陣為

很明顯，系數(shù)矩陣的秩小于變量的數(shù)量。因此，這種線性方程組具有無(wú)限多個(gè)解。換句話說(shuō)，對(duì)于那些不合格的數(shù)據(jù)用戶，他們無(wú)法通過(guò)使用自己的密鑰計(jì)算獲得有關(guān)的確切值的任何有價(jià)值的信息。因此，本文方案可以有效抵抗共謀攻擊。

6 性能分析

本節(jié)將所提方案與其他方案在性能表現(xiàn)方面進(jìn)行了對(duì)比，包括加解密計(jì)算開(kāi)銷、密鑰生成計(jì)算開(kāi)銷、密文長(zhǎng)度和密鑰長(zhǎng)度。在分析計(jì)算開(kāi)銷時(shí)，著重統(tǒng)計(jì)了方案中涉及的一些主要的運(yùn)算，如群元素的冪運(yùn)算、雙線性對(duì)運(yùn)算、標(biāo)量乘法。為了便于理解，將分析中用到的符號(hào)在表1進(jìn)行簡(jiǎn)要說(shuō)明。

表1 符號(hào)示例

為了證明雙線性配對(duì)運(yùn)算比標(biāo)量乘法計(jì)算開(kāi)銷大，表2中對(duì)比了在本文的實(shí)驗(yàn)環(huán)境中2種運(yùn)算的計(jì)算開(kāi)銷。實(shí)驗(yàn)環(huán)境為一臺(tái)搭載Intel的Pentium G620 CPU，2.60 GHz和2 GB RAM機(jī)器，該機(jī)器運(yùn)行Ubuntu Linux 16.04LTS 系統(tǒng)。方案基于PBC庫(kù)（版本0.5.14），選擇了512 bit有限域上的一條超奇異曲線上160 bit的橢圓曲線群，來(lái)實(shí)現(xiàn)80 bit的安全性。實(shí)驗(yàn)結(jié)果是30輪實(shí)驗(yàn)的平均值。從表2可見(jiàn)，一次雙線性配對(duì)運(yùn)算的計(jì)算開(kāi)銷大約是一次標(biāo)量乘法的2～3倍。

表2 各種運(yùn)算計(jì)算開(kāi)銷對(duì)比

從表3中可以清楚地看到，所提方案在多個(gè)方面均優(yōu)于其他方案。密鑰生成和解密的時(shí)間復(fù)雜度均為O(1)，且由于所提方案的密鑰生成階段僅涉及模加運(yùn)算，因此其密鑰生成階段的計(jì)算開(kāi)銷幾乎可以忽略不計(jì)，而較文獻(xiàn)[3]方案和文獻(xiàn)[4]方案更為高效的文獻(xiàn)[11]方案仍需要進(jìn)行2次群元素的冪乘運(yùn)算。解密過(guò)程僅需要一次標(biāo)量乘法，雖然在時(shí)間復(fù)雜度上與文獻(xiàn)[11]方案一樣均為O(1)，但文獻(xiàn)[11]方案仍需要進(jìn)行雙線性配對(duì)運(yùn)算。此外，所提方案中屬性授權(quán)機(jī)構(gòu)為用戶分發(fā)的密鑰長(zhǎng)度是固定的，而非正比于屬性的數(shù)量，且較文獻(xiàn)[11]方案來(lái)說(shuō)，密鑰長(zhǎng)度僅為文獻(xiàn)[11]方案的一半。加密過(guò)程的計(jì)算開(kāi)銷以及密文長(zhǎng)度均正比于OBDD訪問(wèn)結(jié)構(gòu)中有效路徑的個(gè)數(shù)，而非訪問(wèn)結(jié)構(gòu)中屬性的個(gè)數(shù)，這顯然有效降低了方案的計(jì)算和存儲(chǔ)開(kāi)銷，尤其是當(dāng)V較小時(shí)。

表3 性能對(duì)比

7 結(jié)束語(yǔ)

為了保證物聯(lián)網(wǎng)數(shù)據(jù)安全高效的共享，本文應(yīng)用CP-ABE技術(shù)來(lái)對(duì)數(shù)據(jù)進(jìn)行安全的加密，同時(shí)實(shí)施細(xì)粒度的訪問(wèn)控制。基于OBDD 的訪問(wèn)結(jié)構(gòu)提出了一種新型的無(wú)配對(duì)CP-ABE方案。利用橢圓曲線密碼技術(shù)，將原本CP-ABE方案構(gòu)造中復(fù)雜的雙線性配對(duì)運(yùn)算替換為輕量級(jí)的標(biāo)量乘法，從而降低了方案的計(jì)算開(kāi)銷。同時(shí)方案采用OBDD訪問(wèn)結(jié)構(gòu)，該類型訪問(wèn)結(jié)構(gòu)不僅能表示任何關(guān)于屬性的布爾表達(dá)式，還同時(shí)支持訪問(wèn)策略中屬性的正負(fù)值。安全性和性能分析結(jié)果表明，所提方案在DDH假設(shè)下滿足選擇性選擇明文安全，且方案的計(jì)算效率能滿足物聯(lián)網(wǎng)的實(shí)際應(yīng)用需求。