三元非結構肥效模型提高水稻施肥推薦的可靠性

李 娟，章明清*，章贊德，許文江，姚寶全

（1 福建省農業科學院土壤肥料研究所，福州 350013；2 福建省大田縣農田建設與土壤肥料技術推廣站，福建 366100；3 福建省亞熱帶植物研究所，福建廈門 361000；4 福建省農田建設與土壤肥料技術推廣總站，福州 350003）

當前，通過構建氮磷鉀三元肥效模型確定最佳施肥量，是實現水稻計量施肥的重要技術途徑之一[1-2]，其中，二次多項式函數是研究和應用最多的肥效模型種類[3-7]。但是，眾多研究表明，一元和二元二次多項式肥效模型典型式的比例分別僅占60%左右和40.2%[8-9]，三元二次多項式肥效模型的典型式比例則更低至23.6%[10]。由于構建肥效模型時出現了大量非典型式，嚴重削弱了該法的計量精確性和實用價值。盡管國內外學者對此進行了深入研究，提出了許多有意義的改進措施[3]，但該問題至今仍然困擾著計量施肥研究和應用。縱觀這些研究和改進措施中，對二次多項式等函數形式的肥效模型本身是否存在模型設定偏誤及提出改進建議還鮮見研究報道。

研究表明，當前廣泛應用的一元、二元、三元二次多項式肥效模型及其它類似的多項式肥效模型存在明顯的設定偏誤[3]。為此，章明清等[11]提出了一元非結構肥效模型，較好地克服了模型設定缺陷。與一元二次多項式肥效模型相比，新模型在擬合水稻氮磷鉀單因素田間肥效試驗結果時，具有較高的擬合精度、較寬的適用范圍和推薦施肥量較低等優點。為此，在一元非結構肥效模型基礎上，本研究利用氮磷鉀三因素田間肥效試驗結果，探討三元非結構肥效模型的構建方法及其對田間肥效試驗資料的擬合效果，旨在擴大三元肥效模型的適用性，為計量施肥研究和應用提供一種新的模型方法。

1 材料與方法

1.1 水稻氮磷鉀田間肥效試驗設計

近10年來，筆者參加福建省莆田市仙游縣和漳州市平和縣的水稻測土配方施肥工作。兩個項目縣均地處南亞熱帶海洋性季風氣候帶，氣候條件尤其適合水稻生長發育。 稻田土壤類型主要有黃泥田、灰泥田及灰沙田等土屬。為探討三元非結構肥效模型的建模方法，本研究針對這兩個項目縣選擇13個代表性水稻氮磷鉀田間肥效試驗結果作為研究案例。試驗采用“3414”設計方案，即：1) N0P0K0；2)N0P2K2；3) N1P2K2；4) N2P0K2；5) N2P1K2；6)N2P2K2；7) N2P3K2；8) N2P2K0；9) N2P2K1；10)N2P2K3；11) N3P2K2；12) N1P1K2；13) N1P2K1；14)N2P1K1。其中，“2”水平為試驗前當地氮磷鉀推薦施肥量，“0”水平表示不施肥，“1”水平和“3”水平的施肥量分別為“2”水平的50%和150%。供試水稻品種采用當地大面積種植的良種，試驗設計方案和田間管理措施與文獻[12]相同。供試土壤主要理化性狀采用常規方法[13]測定。基礎土壤的主要理化性狀和處理 6) 的施肥量以及各處理的試驗產量結果，分別見表1和表2。

為客觀地評價三元非結構肥效模型的科學性和實用性，截止2017年底，作者收集到近10年來福建早稻、晚稻和中稻的氮磷鉀“3414”設計試驗資料668個 (不包括表1和表2的相關試驗點)。這些試驗資料主要來自福建省水稻主產區完成的肥效試驗結果 (表3)。田間試驗設計方案與文獻[12]相同或相似，不再贅述。

表1 早稻代表性試驗點供試土壤理化性狀及其處理氮磷鉀施肥量Table 1 Physical and chemical properties of soils on the representative sites and fertilization rate

1.2 三元非結構肥效模型的構建

針對二次多項式肥效模型存在的模型設定偏誤和多重共線性等問題[3,14]，章明清等[11]根據水稻氮磷鉀單因素肥效試驗結果，提出了一元非結構肥效模型：

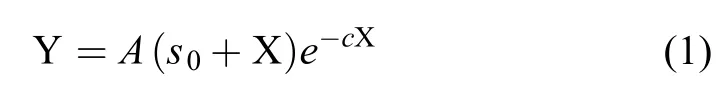
式中：Y表示稻谷產量，X表示施肥量，s0為土壤供肥當量，計量單位均為kg/hm2。c為施肥增產效應系數；A表示施肥量X = 0時土壤肥力與稻谷產量之間的轉換系數，綜合反映了試驗地的土壤生產力。在(1) 式模型中，當施肥量和土壤供肥當量都等于零時，作物產量必等于零。因此，根據植物營養元素功能不可相互替代的原理，三元非結構肥效模型可由如下最簡化的數學形式來描述：

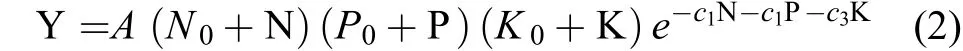
式中：A=AN×AP×AK。數學理論分析表明，(2) 式在一定施肥量范圍內模型存在一個稻谷產量峰值，該峰值對應的施肥量即為最高產量施肥量。因此，根據微積分原理，令 (2) 式的水稻產量Y分別對N、P、K施肥量的導數等于零，得到最高產量施肥量計算式：

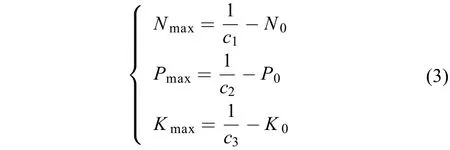
令 (2) 式的水稻產量Y分別對N、P、K施肥量的導數等于稻谷和肥料價格倒數比，得到經濟產量施肥量計算式：

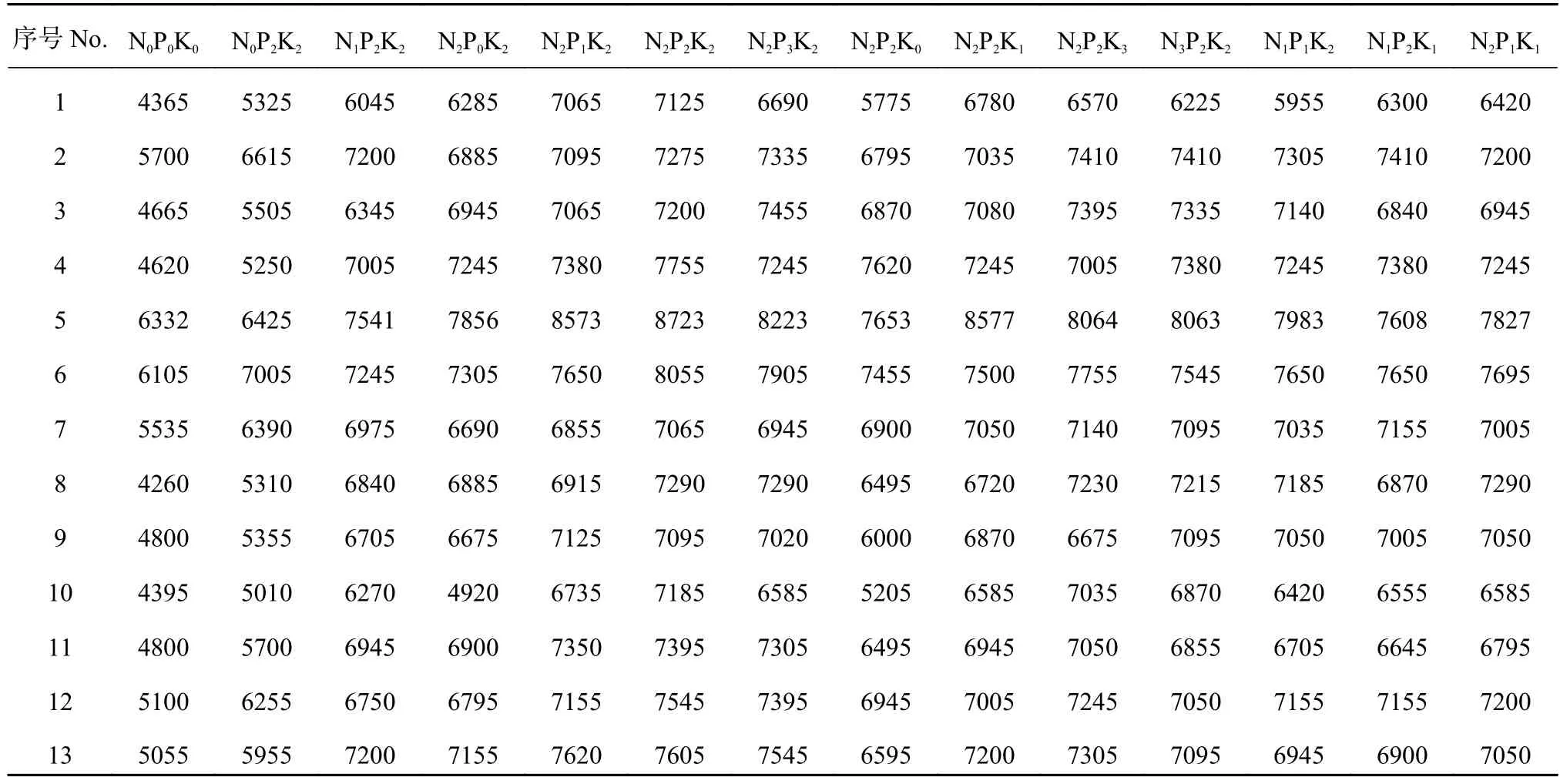
表2 早稻代表性試驗點14個施肥處理的稻谷產量 (kg/hm2)Table 2 Yields of early rice in the 14 treatments in the representative experimental sites

表3 福建省各地區水稻氮磷鉀田間肥效試驗數(n)Table 3 Number of NPK fertilization experiments with “3414” design collected from cities in Fujian Province

1.3 三元非結構肥效模型的參數估計與統計檢驗

(2) 式模型是非線性模型，而且不能直接進行線性化處理，模型參數估計需采用非線性最小二乘法[15]。假設非線性肥效模型為Y =f(X,a)，為求得參數a的估計值，可求解最小二乘問題：

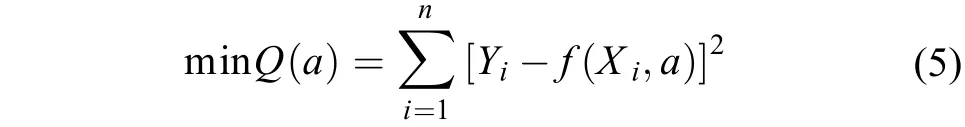
(2) 式模型的回歸顯著性檢驗與三元二次多項式肥效模型相似，但其回歸自由度為6。本研究在計算機上的具體實現則使用MATLAB軟件的nlinfit功能函數進行非線性肥效模型參數估計和統計檢驗，對三元二次多項式肥效模型回歸分析則使用regress功能函數。文中圖形采用MATLAB語言編程繪制，具體計算的數學原理和有關功能函數的使用方法可參閱相關專著[15-16]。

2 結果與分析

2.1 三元二次多項式肥效模型 (TPFM) 的擬合效果

常用的三元二次多項式肥效模型可用如下數學形式來表達：

式中：Y表示模型擬合產量；N、P、K分別表示N、P2O5、K2O施肥量 (kg/hm2)；b0至b9表示模型的肥效系數。根據表1中各試驗點的氮磷鉀施肥量及表2對應試驗點各處理的稻谷產量，采用普通最小二乘法對 (6) 式進行回歸建模 (表4)。結果表明，除1號和2號試驗點外，其它各試驗點建立的肥效模型均達到統計顯著水平。

進一步對表4的三元二次多項式肥效模型進行典型性判別[10]，表明3號和4號試驗點構建的肥效模型，雖然模型系數的代數符號滿足要求，但模型不存在全局極大值，屬于無最高產量點的非典型式；5號試驗點構建的肥效模型，雖然模型系數的代數符號合理且模型存在最高產量點，但屬于推薦施肥量外推的非典型式。6號至13號試驗點建立的三元二次多項式肥效模型滿足作物施肥效應的一般規律，均屬于典型式。

2.2 三元非結構肥效模型 (TNFM) 的擬合效果

對表1和表2的同一批試驗數據，采用 (2) 式進行非線性回歸建模 (表5)。統計檢驗顯示，1號和2號試驗點的顯著水平概率值P由 (6) 式模型未達顯著水平的0.058和0.087提高到顯著水平的0.017和0.010，回歸模型通過了顯著性檢驗；(6) 式模型能通過顯著性檢驗的其它11個試驗點，(2) 模型擬合結果同樣能通過顯著性檢驗，而且，除了10號試驗點外，其它12個試驗點的顯著性概率值P均明顯小于表4的 (6) 式模型相應指標。

表5的三元非結構肥效模型典型性判別[10]結果表明，由 (6) 式模型回歸建模未能通過顯著性檢驗的1號和2號試驗點以及歸屬于非典型式的第3、4、5號試驗點，均轉化成了典型三元肥效模型，模型系數的代數符號、模型最高產量點和推薦施肥量等方面均滿足了作物施肥效應的一般規律；(6) 式模型能得到典型式的6號至13號試驗點，(2) 式模型的建模結果同樣能得到典型式。

因此，統計顯著性檢驗指標F值、擬合優度R2和顯著水平概率值P以及典型式出現比例等方面都表明，(2) 式模型比 (6) 式模型具有更高的擬合精度和更寬的適用范圍。

2.3 三元非結構肥效模型的推薦施肥量

根據表5中各試驗點的三元非結構肥效模型的參數估計結果以及 (3) 式和 (4) 式，計算各試驗點的氮、磷、鉀最高施肥量，并以N 4.3元/kg、P2O55.0元/kg、K2O 5.0元/kg和稻谷2.0元/kg的平均市場價格計算經濟施肥量。結果表明，1號至5號試驗點的推薦施肥量均落在試驗設計的施肥量范圍內，相應的模型預測產量也都落在試驗各處理的產量范圍之內，無異常情況出現。

在根系養分吸收機理模型研究中，為評價機理模型養分吸收量預測值的可靠性，一般都采用在預測值與實測值之間進行一元線性回歸分析[17]。本文采用相同方法考察（2）式模型在推薦施肥量上的可靠性，即：針對6號至13號試驗點的（6）式模型參數估計結果，采用邊際產量導數法計算相應試驗點的氮、磷、鉀的最高施肥量和經濟施肥量，并與（2）式模型對應推薦施肥量繪制成圖1。結果顯示，兩種肥效模型的氮、磷、鉀的最高施肥之間以及經濟施肥量之間都存在顯著水平的線性正相關，說明在三元典型肥效模型前提下，新模型的推薦施肥量對二次多項式模式推薦施肥量具有繼承性和可靠性。同時，線性回歸模型的一次項系數分別為0.876和0.940，表明當三元二次多項式肥效模型推薦施肥量每增加1kg時，三元非結構肥效模型的最高施肥量和經濟施肥量平均只增加了0.876kg和0.940kg，新模型較好地克服了二次多項式肥效模型推薦施肥量偏高的不足[2,18]。

圖1 三元非結構肥效模型和三元二次多項式肥效模型推薦施肥量的相關性Fig. 1 Agreement of the recommended fertilizer rate between ternary non-structural and ternary quadratic polynomial fertilizer response models (TNFM and TPFM)

2.4 三元非結構肥效模型擬合效果評價

分別采用 (2) 式和 (6) 式對收集的 668個“3414”田間試驗建三元肥效模型 (表6)。統計結果表明，目前常用的三元二次多項式肥效模型的典型式平均比例僅為19.5%，而三元非結構肥效模型的平均比例提高到39.1%，是前者的2.0倍，顯著提升了建模成功率。

進一步分析還表明，受多重共線性危害的影響[3,19]，二次多項式肥效模型一次項或二次項的系數代數符號不合理的非典型式平均比例達到32.3%，而消除了多重共線性危害的三元非結構肥效模型的N0、P0、K0或c1、c2、c3等系數符號不合理的模型比例則平均為6.9%，大幅度降低了此類非典型式出現的機率。二次多項式肥效模型的一次項和二次項系數代數符號合理但模型無最高產量點的非典型式平均比例為14.4%；由于非結構肥效模型所具有的數學結構特點，模型系數代數符號合理則必有最高產量點。二次多項式模型系數代數符號合理且存在最高產量點但推薦施肥量外推的非典型式平均比例為4.0%，但非結構肥效模型的此類非典型式比例提高到30.7%，顯示兩種肥效模型在無最高產量點和推薦施肥量外推的非典型式類型出現比例方面有明顯的差別。

3 討論

3.1 三元二次多項式肥效模型的設定偏誤

在肥料效應函數中，單位養分增產量與施肥量的函數關系的不同假設，就會得到數學形式各異和適用性不同的肥效模型[20]。假設增施單位量肥料的增產量和該養分最高產量施肥量與現有施肥量之差成正比，由此推導可得到一元二次多項式肥效模型。該模型被國內外的大量肥效試驗尤其是氮肥試驗結果所證實[20-23]。Cerrato等[24]、楊靖一等[25]和陳新平等[18]對蔬菜、冬小麥和夏玉米的多項式、線性或二次函數+平臺等氮肥效應模型進行了比較研究，表明二次型模型具有較強的通用性。毛達如等[26]對2次、1.5次、0.75次和0.5次的氮磷二元多項式肥效模型比較也顯示，在灌溉地上二次多項式能較好地反映冬小麥的肥效規律。可惜的是，668個水稻氮磷鉀田間肥效試驗表明，三元二次多項式肥效模型典型式的平均比例僅為19.5% (表6)，過低的建模成功率令人不得不懷疑二次多項式肥效模型設定本身的合理性。

對二次多項式的分析表明，該類模型是假設單位養分增產量與施肥量之間的函數關系為線性關系，結果導致最高施肥量之前和最高施肥量之后的施肥效應是對稱關系[3]。這種模型設定忽略了高產耐肥新品種在過量施肥時因作物耐肥特性，使產量降低幅度得到較大程度緩解的當前生產實際。同時也忽略了土壤對養分的緩沖能力從而減輕了過量施肥對作物產量負效應的作用。此外，二次多項式模型的回歸變量間存在強烈的多重共線性[3,14]，制約了普通最小二乘法回歸建模的有效性和統計檢驗的可靠性。上述兩個缺陷是導致當前常用的三元二次多項式肥效模型的典型式比例明顯偏低的重要原因。

針對多項式統計模型的多重共線性問題，數理統計學家已經提出了諸如嶺回歸、主成分回歸、偏最小二乘回歸等有偏估計方法[19,27]，來消除或削弱這種多重共線性的危害。例如，采用主成分回歸技術對福建171個早稻氮磷鉀“3414”試驗結果建立三元二次多項式肥效模型，其典型式的比例從普通最小二乘法的27.5%提高到43.3%[28]。但是，有偏估計只能消除或緩解多重共線性危害，不能有效地解決肥效模型設定的偏誤問題。

表6 三元二次多項式肥效模型和三元非結構肥效模型擬合效果比較Table 6 Fitting effect of ternary non-structural fertilizer response model compared with that of ternary quadratic polynomial fertilizer response model

3.2 三元非典型式的類型和分類方法

在肥效模型研究中，常用的邊際產量導數法計算推薦施肥量的方法僅適用于典型肥效模型，對非典型肥效模型的計算結果則會產生誤導。因此，三元肥效模型典型性判別在推薦施肥中具有重要作用。總結福建省668個水稻氮磷鉀田間肥效試驗結果以及先前的相關田間肥效試驗資料[10]，三元二次多項式肥效模型的非典型式有三種類型。在通過統計顯著性檢驗前提下，從直觀上看，如果肥效模型的一次項系數至少有一個為負數或二次項系數至少有一個為正數 (不考慮交互項系數符號)，因其不滿足作物施肥效應的一般規律，此類肥效模型就屬于模型系數不合理的非典型式，平均占到試驗點總數的32.3% (表6)；第二種類型是模型一次項或二次項系數符號合理，但肥效模型不存在全局最高產量點，此類模型屬于無最高產量點的非典型式，其平均比例占試驗點總數的14.4% (表6)；第三種類型是模型一次項或二次項系數符號合理，而且肥效模型存在最高產量點，但推薦施肥量屬于遠外推結果，此類模型屬于推薦施肥量外推的非典型式，其比例平均占試驗點總數的4.0% (表6)。

與之對應，在表6的建模結果中，三元非結構肥效模型也會存在不同類型的非典型式。在通過統計顯著性檢驗前提下，當模型參數N0、P0、K0、c1、c2、c3中有任何一個或一個以上的參數為負數時，因其違背了施肥效應的一般規律，該類肥效模型就屬于參數符號不合理的非典型式，平均占試驗點總數的6.9%，大幅度低于三元二次多項式肥效模型相同類型的比例。當模型參數N0、P0、K0、c1、c2、c3均為正數時，非結構肥效模型因數學結構特點必有最高產量點，因而不存在無最高產量點的非典型式類型。然而，模型參數代數符號合理但推薦施肥量屬于遠外推的非典型式類型平均達到試驗點總數的30.7%，遠高于三元二次多項式肥效模型相同類型的比例。可以想像，相信為降低遠外推模型比例，非結構肥效模型對試驗施肥量設計具有更高的要求。幸運的是，這一要求在試驗設計中容易做到。

模型擬合過程還表明，“3414”試驗采用多點分散不設重復的試驗方法，無論是多項式肥效模型還是非結構肥效模型，都有相當大比例的試驗點未能通過顯著性檢驗，其中，二次多項式肥效模型的平均比例達到30.1%，非結構肥效模型則為23.4%。另外，未能通過統計顯著性檢驗或者得到典型肥效模型的相關試驗點經常會相對集中出現，說明建模成功與否還和田間試驗質量密切相關。

3.3 三元非結構肥效模型的適用性

研究表明，一元二次多項式肥效模型是一元非結構肥效模型的簡化式和特例[11]。針對三元非結構肥效模型的指數項，根據高等數學的泰勒展開式，即：其中，由于三元非結構肥效模型的參數c1、c2、c3均在10-3量級，若只取展開式的前兩項，則 (2) 式模型可以轉化為Y =A(N0+BN-c1N2) (P0+CP -c2P2) (K0+DK -c3K2) , 其中，B=1 -N0c1，C= 1 -P0c2，D= 1 -K0c3。對該式進行代數式展開，并忽略c1、c2、c3的兩兩乘積項以及c1c2c3的乘積項和NPK三因子交互項，則 (2) 式可以進一步轉化為Y =A(N0P0K0+BP0K0N +CN0K0P +DN0P0K -c1P0K0N2-c2N0K0P2-c3N0P0K2+BCK0NP +BDP0NK +CDN0PK)，結果顯示與 (6) 式具有相同的數學形式。由此可見，三元二次多項式肥效模型是三元非結構肥效模型的簡化式和特例。當某些試驗結果確實使上述忽略項對作物產量影響足夠小時，(2) 式和 (6) 式模型都能得到很好的擬合效果；反之，三元二次多項式模型可能會因過分簡化導致擬合效果較差，而三元非結構肥效模型因未進行這種簡化則可能較好地擬合相關試驗結果。

三元非結構肥效模型假設單位養分增產量與施肥量之間的函數關系為非線性關系，較好地克服了二次多項式肥效模型的設定偏誤；模型本身不能直接進行線性化轉換，較好地克服了多重共線性問題。在668個水稻氮磷鉀田間肥效試驗資料 (表6)中，三元非結構肥效模型的典型式平均比例達到39.1%，是三元二次多項式肥效模型典型式比例的2.0倍。圖1分析表明，新模型推薦的最高施肥量和經濟施肥量與三元二次多項式肥效模型的相應推薦施肥量具有顯著水平的線性正相關，同時較好地克服了推薦施肥量偏高的問題。因此，新模型具有較寬的適用范圍。

4 結論

三元非結構肥效模型較好地克服了三元二次多項式肥效模型的設定偏誤和多重共線性危害，在水稻氮磷鉀施肥效應建模中，具有更高的擬合精度和更寬的適用范圍。