相位差譜法合成人工地震動及其驗證
高 陸 軍
(中鐵五局集團路橋工程有限責任公司,貴州 貴陽 550001)
0 引言
實際地震動是一種強度和頻率均具有非平穩特性的隨機過程[1,2]。目前常用強度包絡函數來刻畫強度非平穩,而對于頻率非平穩,有學者提出用相位差譜的概念來描述[3,4]。地震動相位差譜與地震動時程強度及頻率含量非平穩之間有著重要關系,在地震動空間相關性研究中也有重要應用。
本文考慮地震動空間效應和三維性,基于相位差譜法生成非平穩地震動,并通過頻域擬合目標反應譜法對新合成地震動進行幅值精度迭代調整。最后以人工合成的地震動反應譜為目標反應譜,從PEER中選取實際地震動。將該地震動施加到某三跨高墩鋼構橋上,對本文提出的人工地震動合成方法進行驗證。
1 理論分析
1.1 三角級數法合成地震動
三角級數法是人工合成地震動的常用方法,它具有原理簡單、計算速度快編程簡單等特點。但該方法得到的地震動反應譜和抗震計算的目標反應譜之間存在較大的誤差,精度相對而言不高,不能滿足抗震設計要求。
1.2 強度非平穩
為表征地震波強度非平穩,通過三角級數法合成地震波時,用平穩過程與地震動強度包絡曲線的乘積來刻畫強度非平穩。
三角級數法合成地震動雖然快捷方便,但合成的地震動與實際地震動相比,不具有頻率非平穩特性。特別是對于細長型結構如橋梁等,三角級數法不能考慮地震動的行波效應。
2 基于相位差譜的地震動人工合成
2.1 相位差概念
Ohsaki[12]用相位差譜的概念來體現真實地震動相位角之間的相關特性,相位差是指相鄰頻率對應相位之差,其計算式為:
(1)
其中,k=0.1,…,N/2-1,Δφ(ωk)為相位差;φk和φk+1為相鄰兩個頻率對應的相位角;N為傅里葉變換階數;相位差的定義域為[0,2π]。
假設頻率為0處的相位也為0,則Δφ(0)=0,而其他頻率部分的相位角根據相位差定義計算:
φk=Δφ(ωk)+φk-1
(2)
根據式(2)將區段相位差譜合成相位譜,代入公式中,替換隨機相位角,即合成基于相位差譜的人工地震動。但此時的人工地震動精度不夠,需要進一步迭代修正。
2.2 相位角的統計特性
式(1)為相位差的定義式,不方便用統計的概念來計算相位差概率分布密度函數。根據蒙特卡洛方法,對數正態分布的隨機統計參數可以由正態分布的統計參數得到:
(3)
(4)
其中,μ和σ分別為正態分布序列ck的均值和均方差。再通過相位差和正態序列ck的轉換關系Δφ(ck)=eck,即可生成具有對數分布的隨機相位差譜。
2.3 精度迭代修正
為進一步提高準確率,對合成地震在頻域內進行迭代調整,基本步驟如下:
1)根據時頻關系,并引入單位脈沖反應函數得到人工地震動的反應譜R(ω,c):
(5)
其中,Sa(ω,ζ)為人工反應譜;ω和ζ分別為結構圓頻率和阻尼比;h(·)為單位脈沖反應函數。
2)將人工合成的各頻率分量時程對應的反應譜與目標反應譜之商作為精度控制指標,當該商不在較好精度范圍內時,對其幅值修正并再次合成地震動反應譜,再次做商進行精度修正。按照上述方法多次調整幅值,直到控制指標在滿意精度范圍內為止,即擬合精度迭代計算。
(6)
幅值迭代修正表達式如下:
(7)
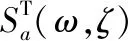
3 準確性驗證
3.1 地震波的選取
為驗證本文合成地震動的準確性,將三角級數法和基于相位差譜法與實際地震動對結構響應進行對比分析。將本文前兩者人工合成的地震動轉化為反應譜,并以該反應譜為目標反應譜,從PEER中選取十條真實地震動。真實地震動與兩條反應譜相互關系見圖1。
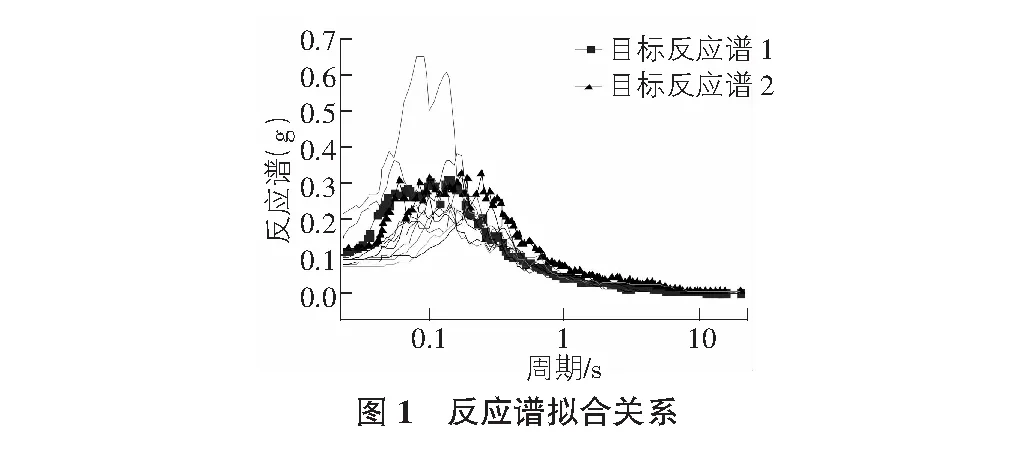
選取擬合度較好的真實地震動作為分析對象,其加速度時程與反應譜如圖2,圖3所示。
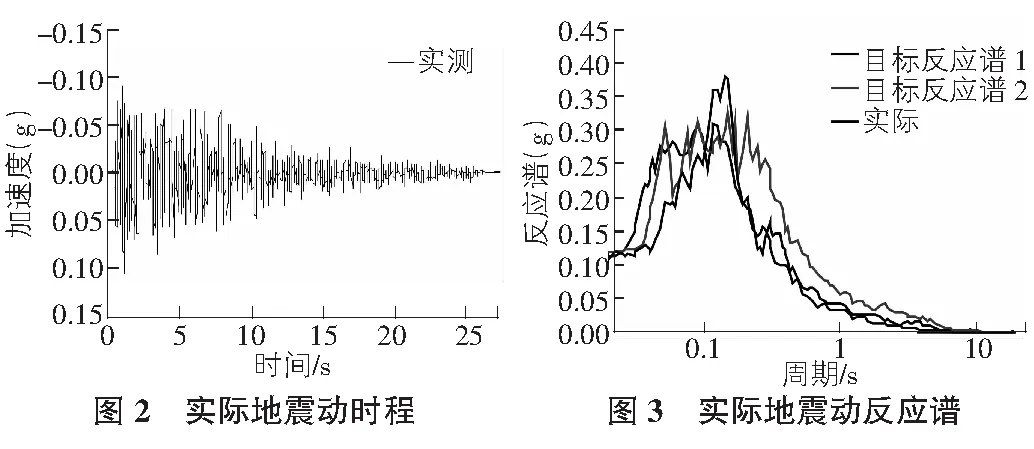
其中,目標反應譜1為相位差譜法合成的地震動反應譜,目標反應譜2是三角級數法合成的地震動反應譜。
3.2 計算模型簡介
以某三跨高墩剛構橋為分析載體,其跨徑組成為85 m+118 m+85 m,墩高度分別為71 m和63 m。將本文中上述人工合成的兩種地震動作為激勵輸入到全橋中,并與施加的真實地震動進行響應對比。剛構橋梁示意圖如圖4所示。
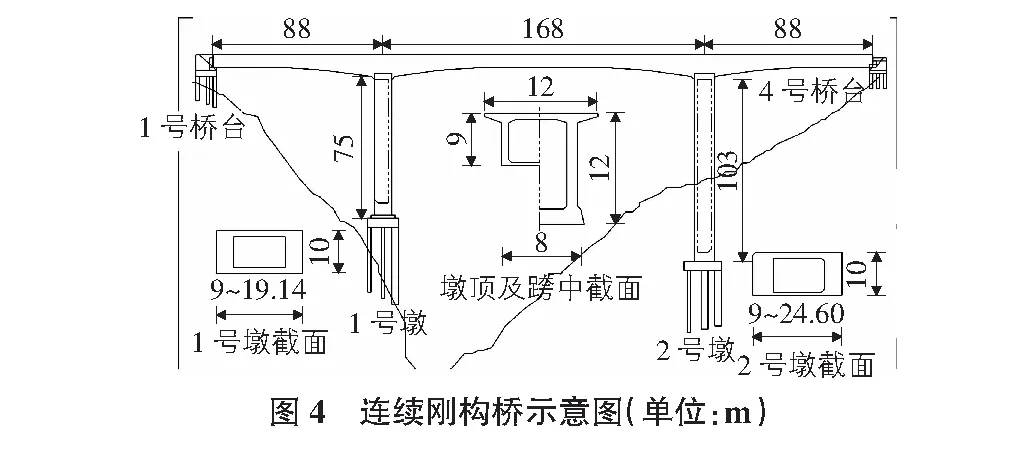
采用一致激勵法,分別計算該剛構橋在上述兩者人工地震動和真實地震動的結構響應,以此來驗證本文方法的準確性。
3.3 響應結果對比驗證
借用通用軟件ANSYS,建立剛構橋有限元模型,并將合成的地震動和真實地震動作用于該模型中進行動力響應分析。將結構響應峰值作為分析對象,主梁和1號墩的縱向位移如圖5,圖6所示,橋墩縱向剪力如圖7,圖8所示,橋墩縱向彎矩如圖9,圖10所示。

分析對比本文兩種人工合成地震動和真實地震動結構動力響應,據圖5~圖8,可獲得如下規律:1)對該橋進行時程分析后,三種地震波產生的縱向位移、墩底剪力和墩底彎矩變化規律基本上一致;2)從圖5,圖6知,人工合成地震動產生的縱向位移響應略比真實地震動的縱向位移大,但總體規律保持一致;3)三種方法所提供的地震動對結構主梁及墩剪力彎矩響應值基本上保持一致,而墩底處基于三角級數合成的地震動要大一些。
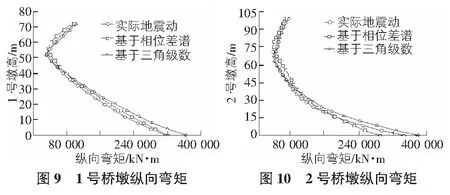
通過時程分析,基于三角級數法、基于相位差譜合成和實測地震動的反應譜大致相似,其縱向的位移、剪力和彎矩分布規律和數值基本一致,故本文合成的地震動具有實際地震動的相應特性,可以用于橋梁結構的地震響應分析。
4 結語
本文基于相位差譜合成人工地震動,得出了以下結論:
1)相位差譜法合成地震動克服了三角級數法缺點,更好地表征地震動強度非平穩和頻率非平穩性,更加符合真實地震動,為抗震研究提供了基礎;
2)通過蒙特卡洛方法,將具有對數正態分布的相位差譜轉化為正態分布的統計參數特性。用目標反應譜對合成的反應譜進行迭代擬合精度修正;
3)基于三角級數法和實測地震波兩種方法對基于相位差譜法合成的地震波進行驗證,通過剛構橋的動力分析證明其準確性。

