采用混合算法優化車輛被動懸架參數及仿真

王秀梅,張慶濤,王 雨

(1.常州機電職業技術學院 車輛工程學院,江蘇 常州 213164; 2.煙臺工程職業技術學院 教務處,山東 煙臺 264006; 3.同濟大學 汽車學院,上海 201804)

自20世紀80年代以來,汽車在中國市場得到了迅速發展.在人們日常生活中,汽車已成為不可缺少的重要交通工具.當前,中國的汽車市場競爭越來越激烈,人們對汽車行駛的安全性和平穩性要求也越來越高.汽車行駛的穩定性和舒適度會受到懸架系統的影響[1].車輛懸架包括主動懸架、半主動懸架及被動懸架3個部分[2].被動懸架因剛度和阻尼系數很難調節,對于不平整路面,車輛受路面激勵導致振動現象較為嚴重.因此,研究被動懸架參數優化方法,設計優良的懸架系統參數,對于促進汽車行駛的穩定性具有重要意義.

當前,國內外學者對懸架系統進行了深入研究.例如:文獻[3-4]采用改進粒子群算法優化車輛懸架參數,創建車輛被動懸架模型,推導出車輛垂直方向運動方程式,構造優化目標函數,采用改進粒子群算法進行優化,通過Matlab軟件進行仿真,提高了駕駛員乘坐的舒適性.文獻[5-6]采用遺傳算法優化車輛懸架系統參數,創建了彈性支撐耦合振動模型,設置車輛多目標函數,采用遺傳算法對目標函數進行優化,提高了車輛行駛的平順性.文獻[7-8]采用觀察算法研究了車輛振動模型,根據濾波噪聲建立路面激勵模型,創建空氣懸架非線性振動模型,通過仿真驗證車輛振動幅度,改善了車輛行駛的穩定性.但是,以往研究車輛懸架模型在受到復雜路面激勵時,容易造成車輛振動幅度較大.對此,本文建立車輛振動數學模型,由牛頓第二定律推導了車輛垂直方向振動約束微分方程式.構造優化目標函數,采用混合算法對4自由度1/4車輛振動模型進行優化.將優化結果進行動力學仿真,并且與優化前的仿真結果進行對比分析,為提高車輛行駛的穩定性和舒適性提供理論基礎.

1 車輛振動數學模型

結合彈簧阻尼質量系統,本文建立了包含駕駛座椅及駕駛員局部身體輪廓的1/4車輛振動模型,簡化后如圖1所示.

在圖1中:zh和mh分別表示駕駛員垂直位移和駕駛員質量;kb和cb分別表示駕駛員身體剛度和阻尼系數;zc和mc分別表示駕駛員座椅垂直位移和質量;kc和cc分別表示駕駛員座椅剛度和阻尼系數;zs和ms分別表示簧上質量組件垂直位移和質量;ks和cs分別表示懸掛彈簧剛度和阻尼系數;zu和mu分別表示簧下質量組件垂直位移和質量;kt表示輪胎剛度;zr表示道路激勵垂直位移;A表示路面不平整高度;l表示路面不平整寬度.

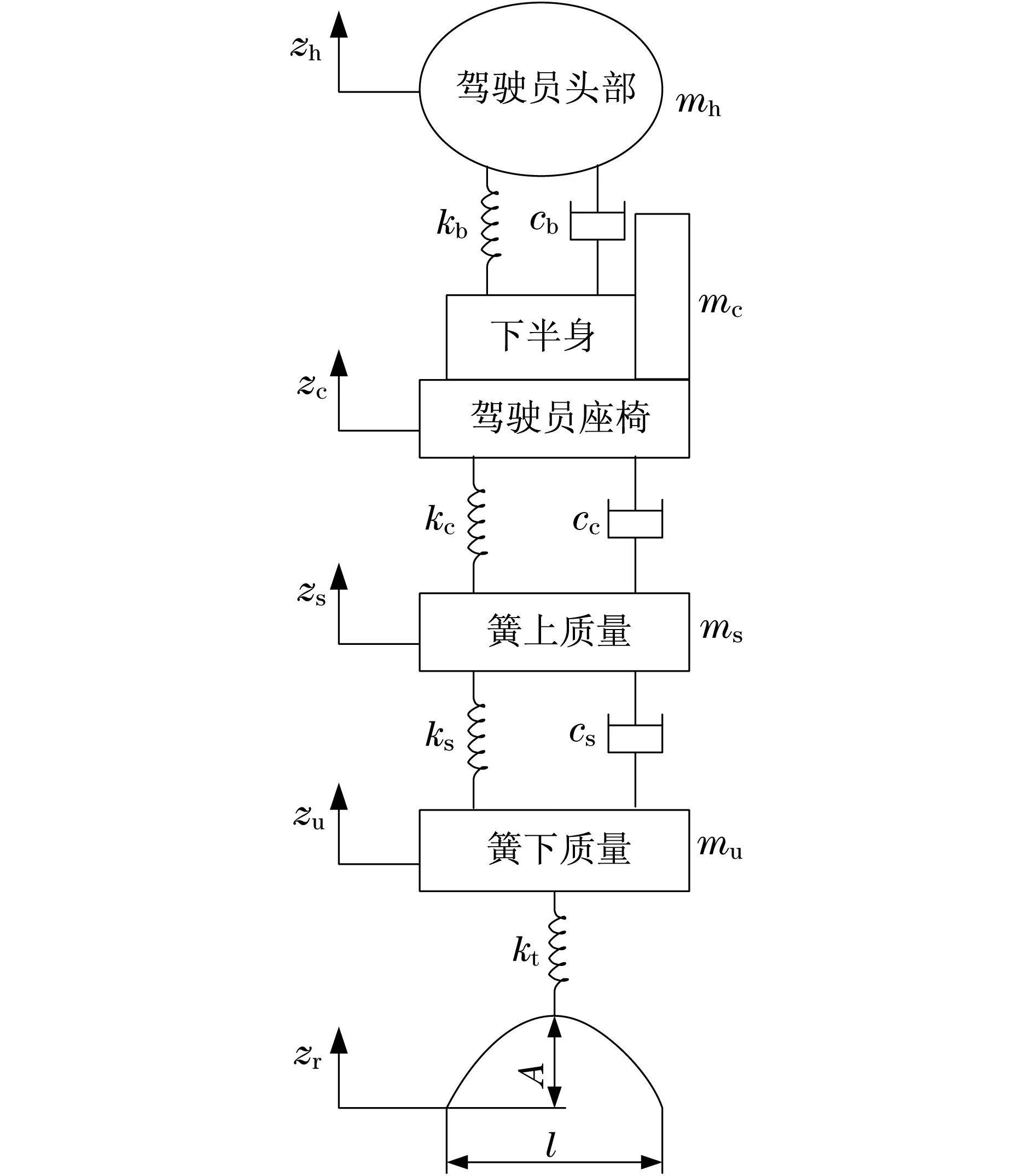
圖1 車輛振動1/4模型Fig.1 Quarter model of vehicle vibration

2 車輛振動運動方程

假設車輛在行駛過程中遇到地面凸起物,物體形狀如圖2所示.

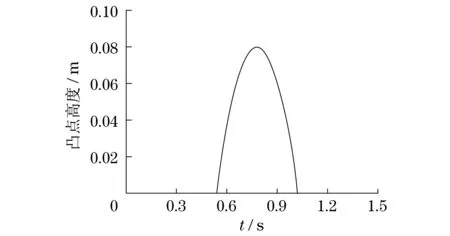
圖2 道路不平整斷面圖Fig.2 Road irregularity section map

汽車行駛受到地面不平整凸起物激勵后的垂直方向的位移運動方程式[9]如下:

(1)

式中:v為車輛行駛速度(m/s);d為車輛前輪軸與后輪軸間的距離(m);t為車輛通過路面凹凸不平整的前輪與后輪時間差(s).

結合圖1的受力分析,根據牛頓第二運動定律可分別推導出簧上質量、簧下質量座椅及駕駛員頭部關系式為

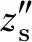
3 車輛被動懸架參數優化

3.1 優化目標函數

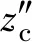
(8)

設計變量參數的取值范圍[10]:60 kg≤mc≤80 kg,228 kg≤ms≤352 kg,16 kg≤mu≤32 kg,15 000 N/m≤kc≤22 000 N/m,19 000 N/m≤ks≤25 000 N/m,120 000 N/m≤kt≤160 000 N/m,1 400 Ns/m≤cc≤1 700 Ns/m,900 Ns/m≤cs≤1 100 Ns/m.

3.2 混合算法

3.2.1粒子群優化算法

粒子群優化算法(Particle Swarm Optimization,PSO)是新發展起來的一種尋優算法.從初始種群隨機解出發,通過迭代搜索全局的最優解[11].PSO搜索全局最優值,不斷地對比群體極值G和個體極值Pi,從而決定是否迭代粒子的速度和位置.粒子速度和位置搜索迭代方程式[11]為

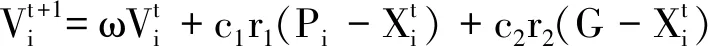
(9)

(10)

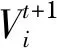
為了更好平衡局部、全局尋優能力,慣性權重系數ω采取線性遞減方式進行修改,即

(11)

式中:t為當前迭代次數;T為最大迭代次數;ω0為初始權重;ω1為最終權重.

3.2.2遺傳算法

由于PSO隨著迭代次數增加容易陷入局部最優解,因此,采用遺傳算法耦合粒子群優化算法,對粒子的局部最優值進行交叉和變異,從而搜索出全局最優解.具體操作如下:

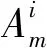
(12)

式中:r為[0,1]的隨機因子.

變異為了維持種群產生多樣性,種群個體實行變異操作,產生更加優秀個體,變異操作方程[13]為

式中:Amin,Amax分別為粒子的下界和上界;a為可調參數.

4 仿真及分析

采用混合算法對被動懸架參數進行優化:種群大小為100,最大迭代次數為300,慣性權重系數設置為ω0=0.85,ω1=0.45,速度更新因子為c1=c2=2,隨機慘數為r1=r2=0.5,交叉概率為0.02,變異概率為0.7.被動懸架參數優化結果如表1所示.

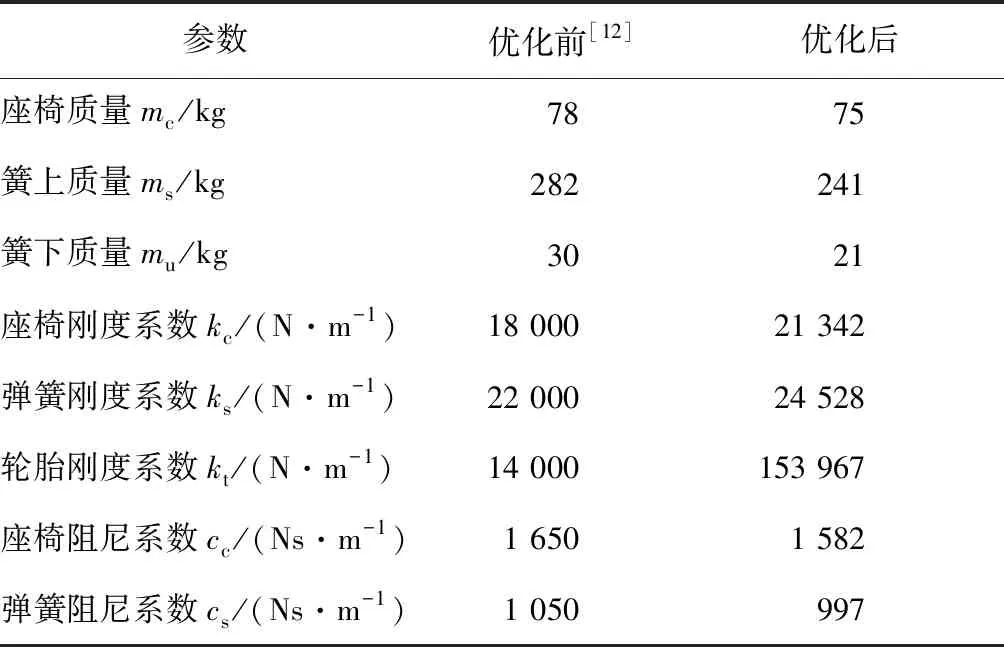
表1 被動懸架優化后參數Tab.1 Optimized parameters of passive suspension

假設車輛行駛的速度v=60 km/h,地面不平整物體高度A=0.08 m,寬度l=0.5 m,駕駛員質量為mh=60 kg,其他參數如表1所示.采用Matlab軟件對車輛振動進行仿真驗證,并與優化前的仿真結果進行對比.其中,路面激勵作為仿真模型的輸入量,如圖1所示.簧上質量組件垂直方向的位移仿真結果如圖3所示,簧上質量組件垂直方向的加速度仿真結果如圖4所示,駕駛員座椅垂直方向的加速度仿真結果如圖5所示.

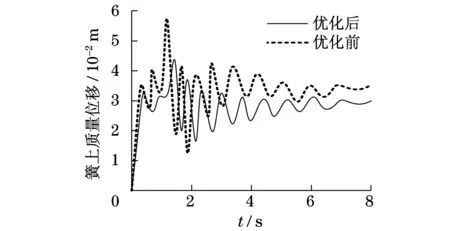
圖3 簧上質量位移仿真結果Fig.3 Simulation results of mass displacementon spring

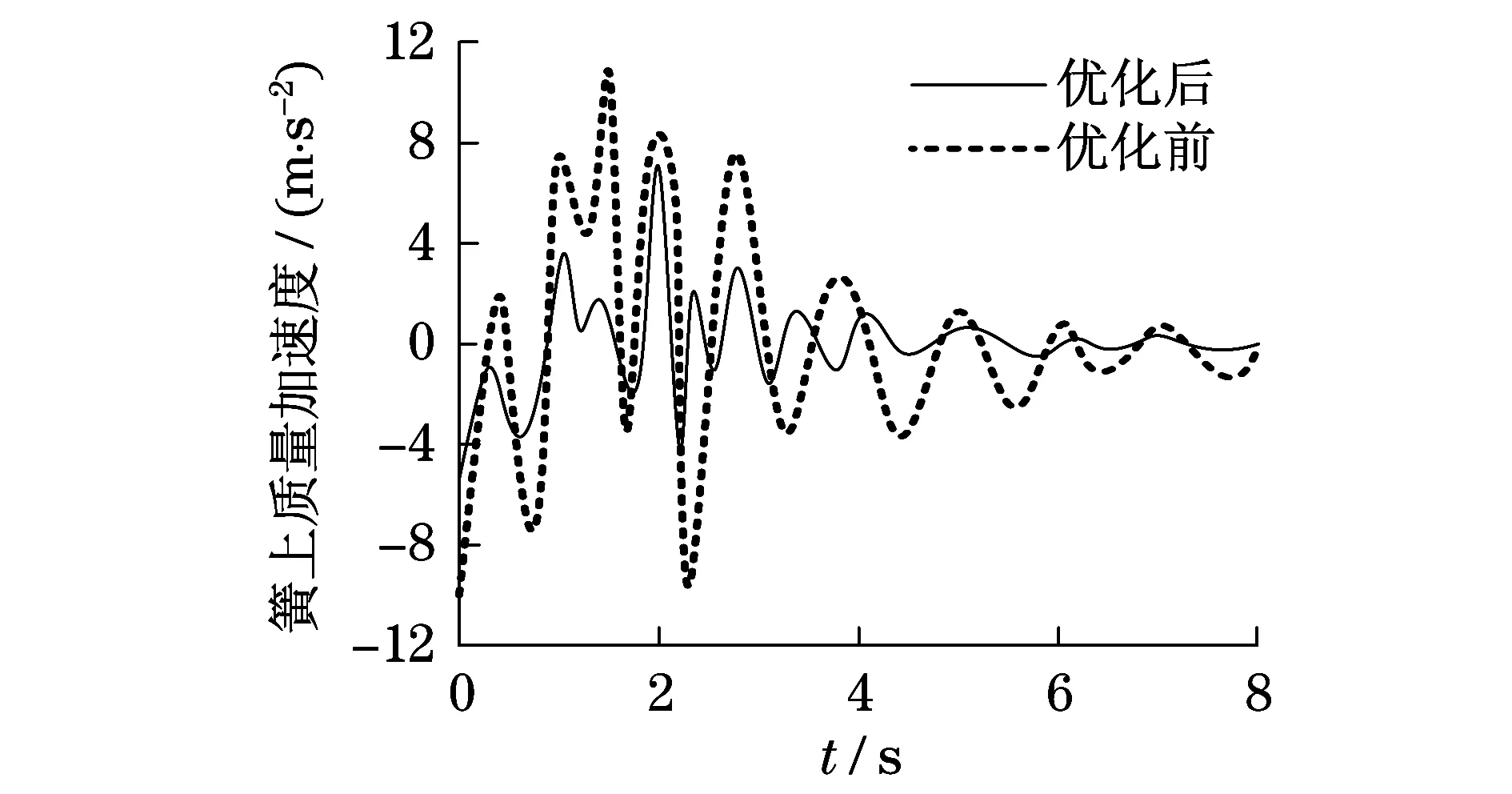
圖4 簧上質量加速度仿真結果Fig.4 Simulation results of mass accelerationon spring

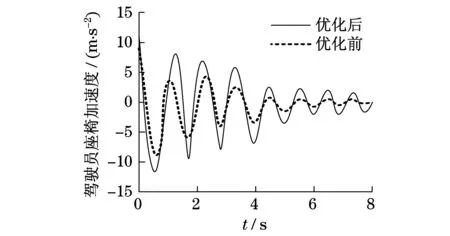
圖5 駕駛員座椅加速度仿真結果Fig.5 Simulation results of driver seat acceleration

根據圖3～圖5可以看出:1/4車輛振動模型簧上質量組件垂直方向位移、加速度及駕駛員座椅垂直方向的加速度變化曲線,以最大值和曲線的上下波動程度作為評價指標.

由圖3可知:采取混合算法對1/4車輛振動模型的目標函數進行優化后,簧上質量組件垂直方向的位移最大值為4.35 cm,位移曲線上下波動幅度較小;而優化前簧上質量組件垂直方向的位移最大值為5.75 cm,位移曲線上下波動幅度較大.

由圖4可知:采取混合算法對1/4車輛振動模型的目標函數進行優化后,簧上質量組件垂直方向的加速度最大值為7.12 m/s2,加速度曲線上下波動幅度較小;而優化前簧上質量組件垂直方向的加速度最大值為10.98 m/s2,加速度曲線上下波動幅度較大.

由圖5可知:采取混合算法對1/4車輛振動模型的目標函數進行優化后,座椅垂直方向的加速度最大值為8.95 m/s2,加速度曲線上下波動幅度較小;而優化前座椅垂直方向的加速度最大值為11.95 m/s2,加速度曲線上下波動幅度較大.

因此,與優化前相比較,本文采用混合算法優化后的簧上質量組件垂直方向的位移、加速度及座椅垂直方向的加速度峰值分別降低了24.3%,35.2%和25.1%.同時,本文優化后的簧上質量組件垂直方向的位移、加速度和座椅垂直方向的加速度曲線上下波動幅度較小,車輛行駛經過地面不平整物體時,車輛抖動程度較小,運動比較平穩.

5 結語

本文研究了車輛振動1/4模型,推導了車輛垂直方向的座椅運動方程式.采取混合算法對模型參數的目標函數進行優化.給出了車輛振動模型變量參數的約束范圍.采用Matlab對座椅垂直方向的位移和加速度進行仿真.同時,與優化前的仿真結果進行比較.仿真結果顯示:優化后的車輛行駛經過不平整地面時,座椅垂直方向所產生的位移和加速度峰值降低,上下波動幅度減弱.車輛行駛經過障礙物時,振動程度得到了改善,提高了駕駛員乘坐的舒適度.