捆綁火箭POGO振動動力學模型的研究

周星光，孫 冰，翟師慧，湯 杰

(1. 上海航天精密機械研究所，上海 201600； 2. 北京航空航天大學 宇航學院，北京 100083)

0 引言

POGO振動是指液體火箭結構系統與推進系統相互耦合而產生的縱向不穩定振動，在低頻振動中占有不可忽視的地位[1]。POGO振動不僅損害航天器自身的功能及設施，還會嚴重威脅宇航員的生命健康[2-3]。因此，POGO振動的抑制對于液體火箭的設計非常重要。

如今對POGO振動的研究眾多，但研究模型大多數是單組元模型或者是沒有考慮耦合的雙組元模型[4-11]，對液體捆綁火箭的POGO振動分析較少。文獻[12]中給出了單組元模型中蓄壓器的最佳設置位置，但未分析捆綁火箭模型。文獻[13]中給出了火箭飛行過程中各部件產生的作用力，但未分析這些作用力對POGO振動的影響程度。

POGO 振動穩定性方法有許多種，但其實質都是一樣的，即特征方程根的實部為負時，系統是穩定的；否則是不穩定的。系統阻尼比為特征方程根的實部與系統特征頻率的比值，則液體捆綁火箭 POGO振動仿真模型的穩定性條件變為：如果系統阻尼比為正，則系統是穩定的；如果為負，則系統失穩。本文搭建了液體捆綁火箭動力學仿真模型，分析了蓄壓器的位置對捆綁火箭POGO振動抑制效果的影響，以及各個部件處產生的作用力對捆綁火箭POGO振動的影響。

1 設計思路

通過Rubin[13]模型，考慮了助推段與芯級之間的耦合關系，搭建了雙組元液體捆綁火箭動力學仿真模型。在捆綁火箭中，蓄壓器可抑制POGO振動，但其安裝方式共有15種。通過調整蓄壓器的位置，分析火箭飛行過程中泵、貯箱、直管、推力室處產生的作用力對POGO振動的影響程度，來簡化液體捆綁火箭POGO振動動力學模型。

2 液體捆綁火箭動力學模型的建立

參考文獻[13]中貯箱、波紋管、直管、蓄壓器、泵、推力室等部件的動力學方程，以及貯箱、直管、泵、推力室產生的作用力動力學方程，基于AMESim建模軟件的二次開發平臺AMESet，構建液體捆綁火箭推進系統的貯箱、波紋管、直管、蓄壓器、泵、推力室等部件模塊。

捆綁火箭的POGO耦合系統由氧路的耦合系統和燃料路的耦合系統組成，以氧路的耦合系統為例，如圖 1 所示。

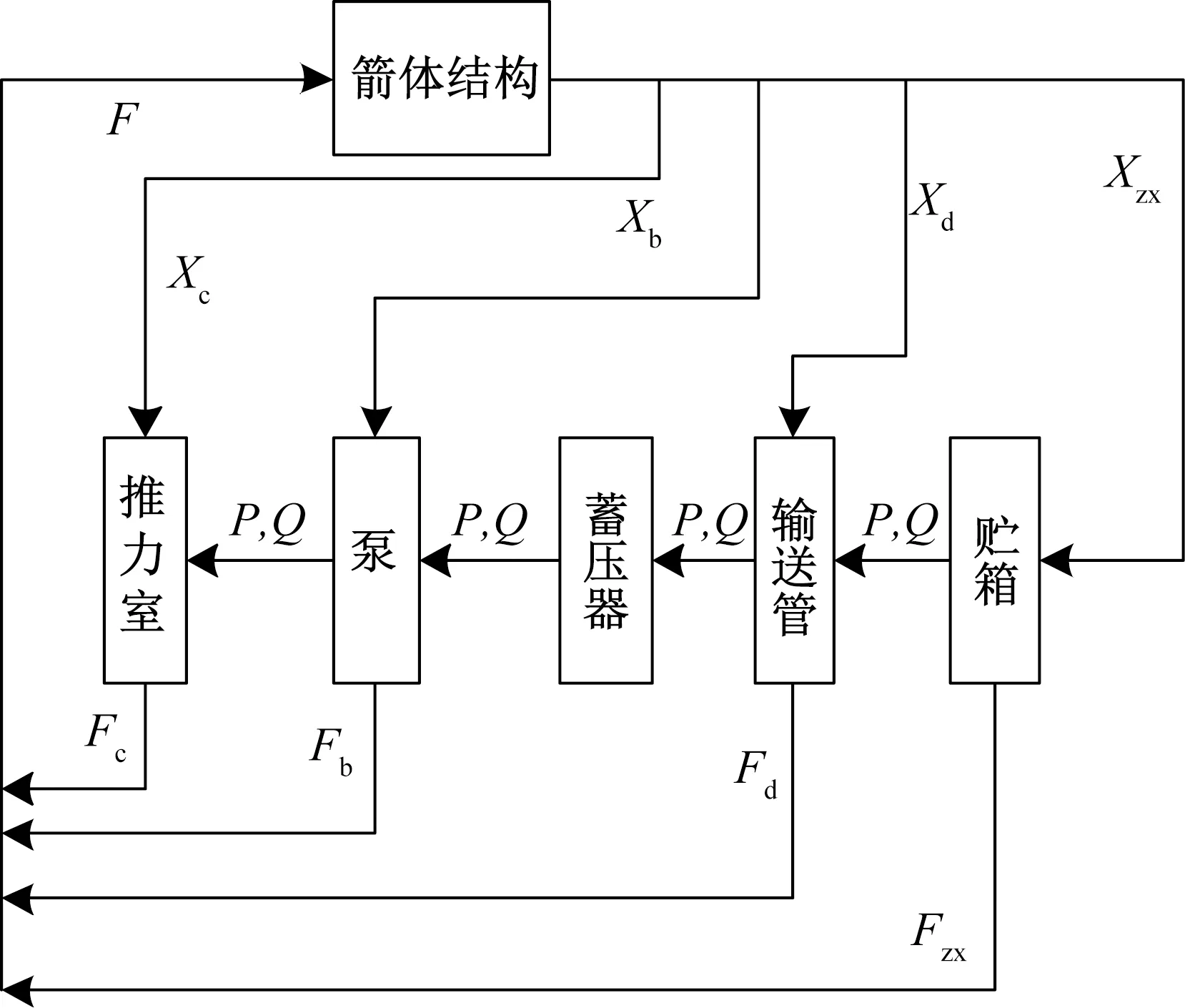
圖1 氧路耦合系統Fig.1 Oxygen circuit coupling system

圖1中各部件之間通過脈動壓力(P)和脈動流量(Q)相互聯系。圖中：vc，vb，vd和vzx分別表示箭體結構在推力室、泵、直管、貯箱處反饋回來的縱向振動速度；Fc，Fb，Fd和Fzx分別表示推力室、泵、直管、貯箱處產生的作用力。

在貯箱處產生的作用力

(1)

式中：Qzx為貯箱處的脈動流量；β為單位面積上的脈動壓力；ρ為推進劑的密度；Pzx為貯箱處的脈動壓力；Azx為貯箱的橫截面積；Nzx為貯箱處的模態參數。

在直管處產生的作用力

(2)

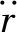
在泵處產生的作用力

Fb=PbiAbiNbi-PboAboNbo+

(3)

式中：Pbi，Pbo為泵入口和出口處的脈動壓力；Abi，Abo為泵入口和出口處的橫截面積；Nbi，Nbo為泵入口和出口處的模態參數；Ws為穩態流量；Qbo為泵出口處的脈動流量。

在推力室處產生的作用力

Fc=-AtCfPcNc

(4)

式中：At為推力室的喉部面積；Cf為推力系數；Pc為推力室內的壓力；Nc為推力室的模態參數。

在廣義坐標系下描述箭體結構縱向振動的方程為

(5)

式中：Mi，Ci，Ki，φi分別為第i階模態質量、阻尼、剛度和振型列陣；Fi為第i階廣義力。根據式(5)，在AMESet中完成液體捆綁火箭結構系統模塊的構建。芯級和助推器參數見表1，捆綁火箭的縱向模態參數見表2。

在此基礎上，引入貯箱、直管、泵和推力室的縱向振動速度和加速度信號反饋，參考文獻[12]中的蓄壓器在單組元模型中的最佳位置，在AMESim中搭建了液體捆綁火箭動力學仿真模型，如圖2所示。

表1 芯級和助推器參數

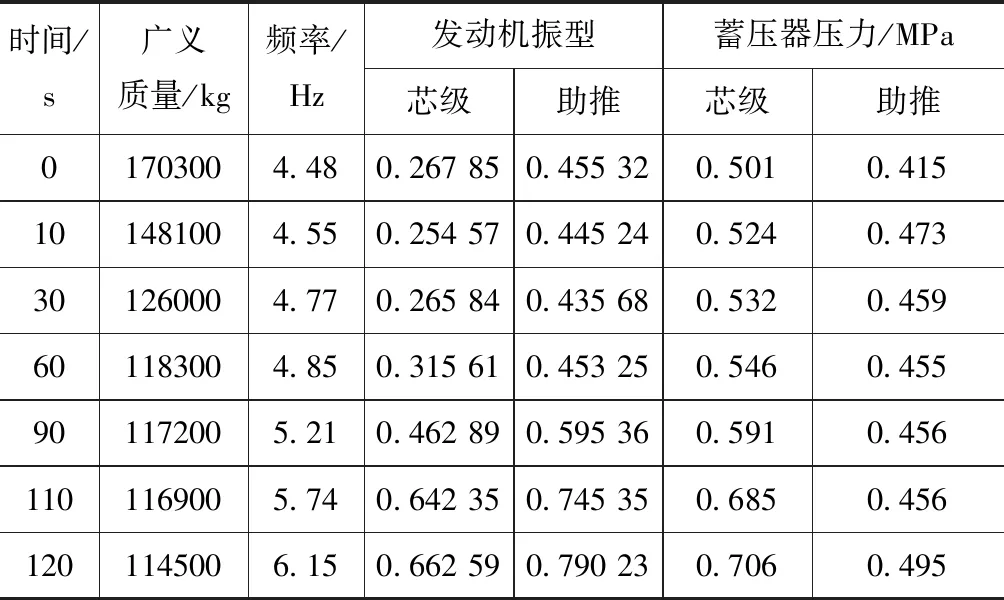
表2 捆綁火箭的縱向模態參數

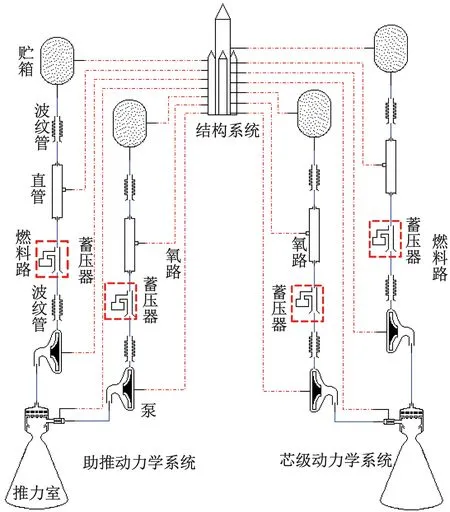
圖2 液體捆綁火箭動力學模型Fig.2 Dynamic model of liquid bundled rocket

圖2中的模型主要由助推動力學系統、芯級動力學系統和結構系統3大部分組成，其中助推動力系統共有4個。助推動力學系統和芯級動力學系統分別由燃料路和氧路構成，由上至下分別為貯箱、波紋管、直管、蓄壓器、波紋管、泵和推力室。結構系統與各個部件之間相連的虛線表示箭體結構反饋回來的縱向振動速度和縱向振動加速度信號，各個部件之間的實線表示脈動壓力和脈動流量。

為驗證模型的正確性，利用建立好的各部件模塊，搭建了文獻[14]中的單路耦合模型，如圖3所示。

圖3 單組元模型Fig.3 Single component model

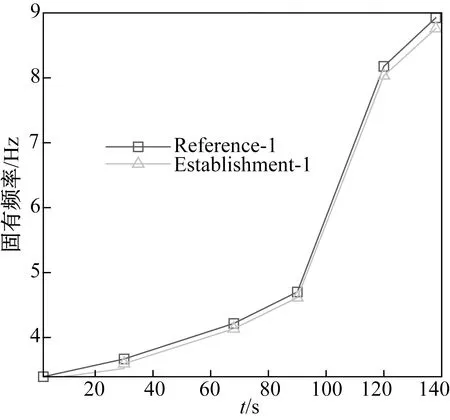
圖4 固有頻率Fig.4 Natural frequency

圖5 系統阻尼比Fig.5 System damping ratio

將文獻[14]中的數據代入，比較固有頻率f和系統阻尼比ξ，如圖4，5所示，Reference-1和Reference-2為文獻[14]中的固有頻率曲線和系統阻尼比曲線，Establishment-1和Establishment-2為圖3模型仿真得到的固有頻率曲線和系統阻尼比曲線。定量計算結果表明，固有頻率與系統阻尼比的偏差在2%以內，可見所建立的各部件模塊是正確的。這也說明用各部件模塊搭建捆綁火箭模型可行。

3 仿真試驗及結果分析

3.1 蓄壓器的位置對POGO振動的影響

液體火箭 POGO 振動系統穩定性條件為：任意時刻，若系統阻尼比為正，則POGO振動系統是穩定的；若系統阻尼比為負，則POGO振動系統是不穩定的。通過分析系統阻尼比提升量隨時間的變化，得到對POGO振動抑制效果最好的蓄壓器位置。

圖2中給出可能設置蓄壓器的4個位置，分別為助推段氧路(zo)、助推段燃料路(zf)、芯級氧路(xo)、芯級燃料路(xf)，故蓄壓器的設置共有16種，如表3所示。

表3中的“■”表示在該位置上設置蓄壓器。為確定蓄壓器的位置，針對這16種設置，在頻域進行仿真，以不設置蓄壓器的模型(表3中的種類1)得到的系統阻尼比為標準，得到其他設置種類的系統阻尼比提升量(Δξ)隨時間的變化曲線，如圖6所示。

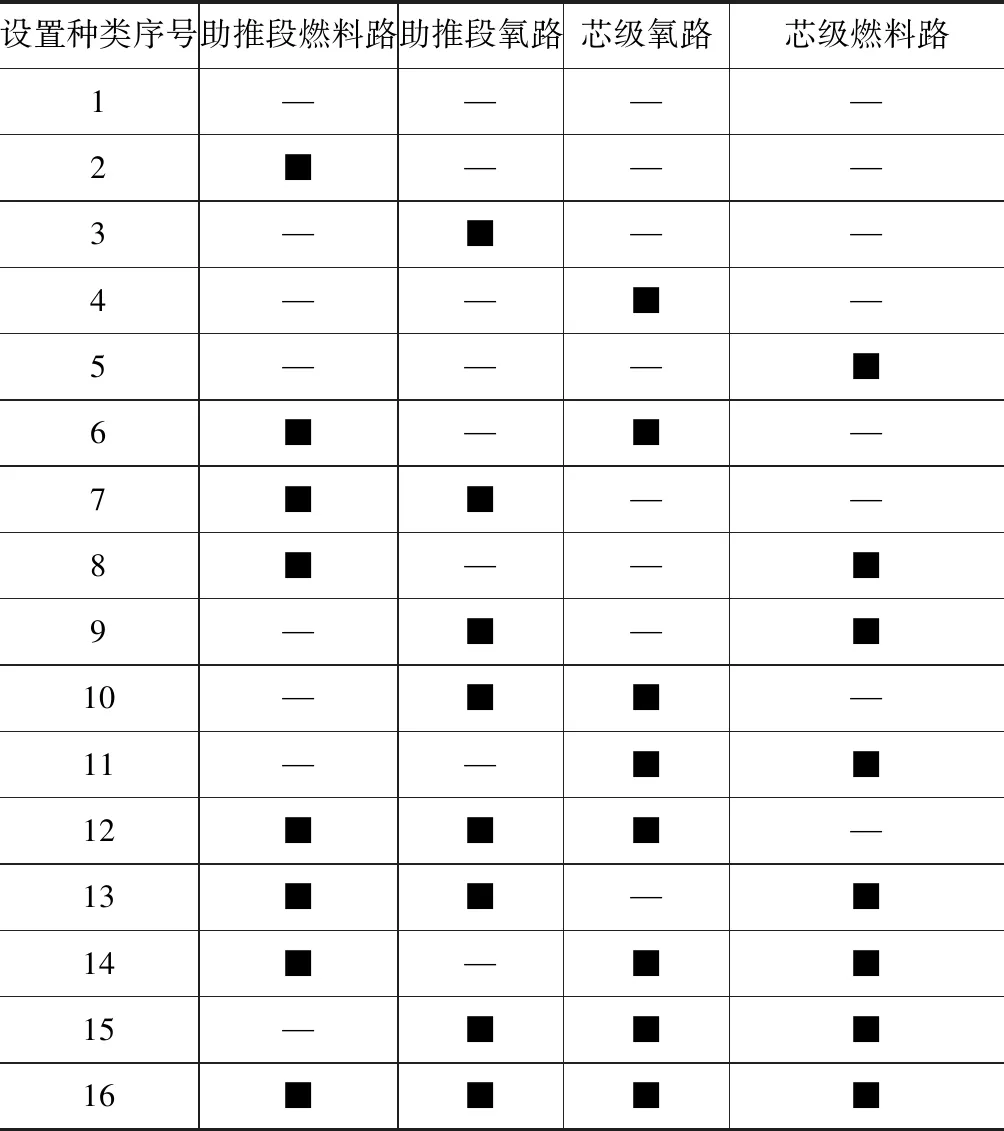
表3 蓄壓器的安裝

圖6 系統阻尼比變化量Fig.6 System damping ratio variation

圖6中的曲線2～16分別表示表3中序號為2～16的15種蓄壓器的設置情況。

由圖6(a)可知：曲線2和5系統阻尼比的變化量幾乎為0，說明蓄壓器只設置在助推段燃料路或芯級燃料路，對POGO振動的抑制效果很差。在曲線2中，雖然在120 s時，系統阻尼比降低，但對比曲線3和曲線4可知：圖6(a)中曲線2對系統阻尼比的提升量最高。對比曲線2與3和曲線4與5可知：在助推段和芯級中，蓄壓器設置在氧路對POGO振動抑制效果比設置在燃料路時要好。

由圖6(b)可知：曲線6，8，9，11的系統阻尼比提升量很小，說明蓄壓器在這幾種設置下，對POGO振動的抑制效果較差。曲線7和10的系統阻尼比增加量很明顯，曲線10的系統阻尼比增加量最大。對比曲線9與10和曲線6與10可知：在助推段和芯級中，蓄壓器設置在氧路對POGO振動抑制效果比設置在燃料路時要好。

由曲線3和曲線10可知：曲線10系統阻尼比提升量更大，故蓄壓器設置在芯級氧路和助推段氧路時對POGO振動的抑制效果較好。

對比曲線3與7和曲線3與10可知：增加一個蓄壓器，系統阻尼比的提升量明顯增加。繼續增加蓄壓器的數量，由圖6(c)可知：系統阻尼比的提升量很明顯。將曲線16分別與曲線12和15作對比，可發現蓄壓器在4個位置上都設置時，系統阻尼比的增加量比在3個位置上設置時要小。這是因為在整個系統中，每增加一個部件，就會使系統阻尼比變得更低，也就會使POGO振動更容易發生。雖然蓄壓器可抑制POGO振動效果，但蓄壓器過多會降低POGO振動的抑制效果。圖6(c)中曲線13和14是因在芯級和助推段的氧路上都沒有設置蓄壓器，故系統阻尼比的提升量較小，這也說明在助推段和芯級中，蓄壓器設置在氧路對POGO振動抑制效果比設置在燃料路時要好。

曲線10和曲線15很相近，系統阻尼比的提升量都很大，但曲線10只設置了2個蓄壓器，系統的可靠性更高且運載火箭的質量更輕。由此可知：蓄壓器設置在芯級氧路和助推段氧路對POGO振動的抑制效果最好。

3.2 作用力對POGO振動的影響

以蓄壓器設置在助推段氧路和芯級氧路作為仿真模型，分析了貯箱、直管、泵、推力室處產生的作用力對系統阻尼比的影響。以考慮全部作用力得到的系統阻尼比為標準，分析了不考慮這幾個外力時系統阻尼比的相對變化量(dξ)，如圖7所示。

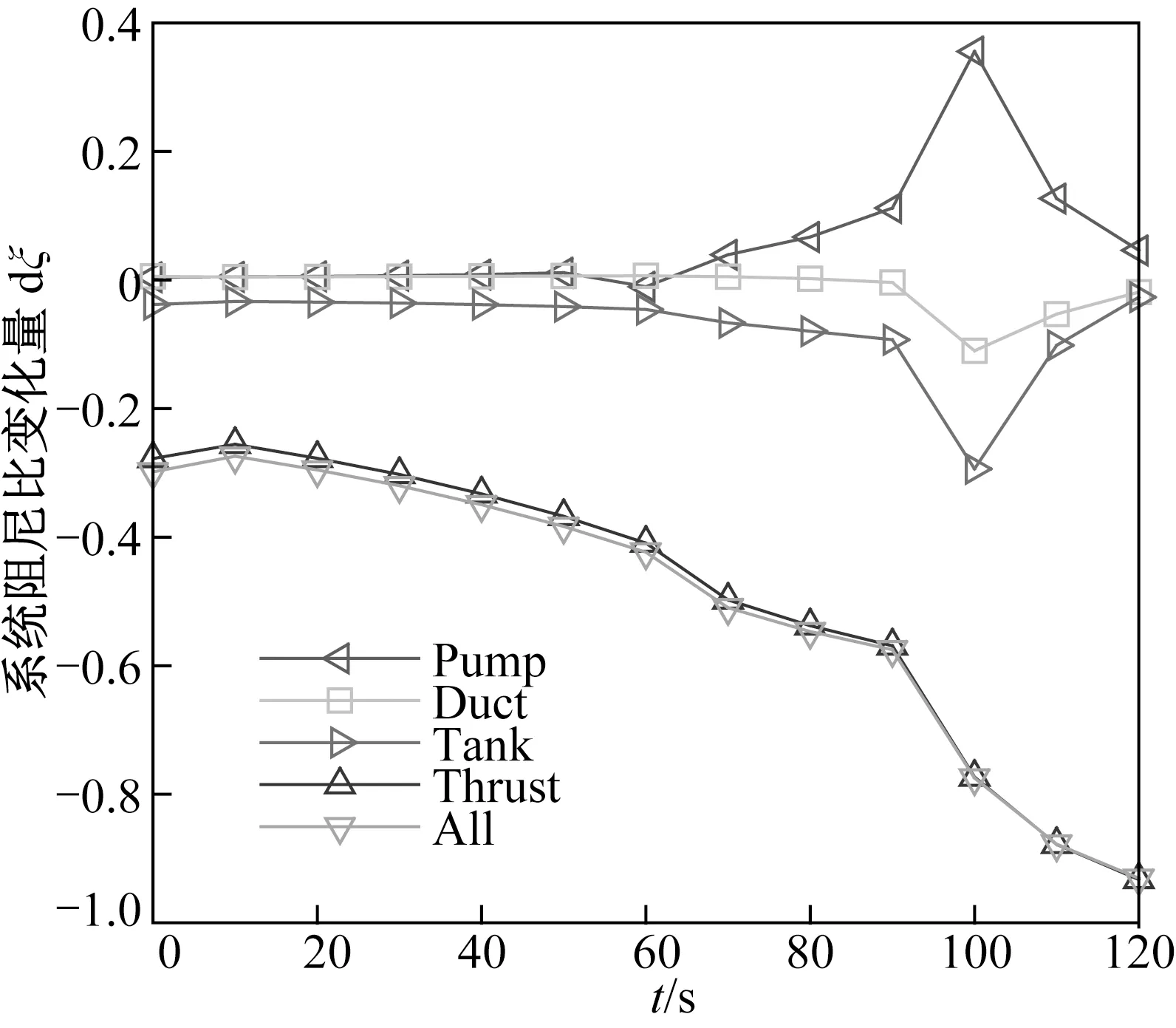
圖7 作用力對系統阻尼比的影響Fig.7 Effect of force on system damping ratio

圖7中的Pump，Duct，Tank，Thrust，All分別表示不考慮泵處作用力、直管處作用力、貯箱處作用力、推力室處作用力和所有作用力的系統阻尼比相對變化量曲線。

由圖7可知：Pump，Duct和Tank這3條曲線雖然在100 s時，系統阻尼比產生了相對較大的波動，但是整體來看系統阻尼比的波動很小。由此可知：泵、直管和貯箱處的作用力對系統阻尼比的影響很小，也就是對POGO振動的影響很小。

對比分析Thrust與All這2條曲線可知：這2條曲線幾乎重疊在一起，說明不考慮推力室處產生的作用力時，其他作用力對系統阻尼比幾乎沒有影響。推力室處產生的作用力對系統阻尼比的影響與所有的作用力對系統阻尼比的影響幾乎相當，即推力室處產生的作用力對系統阻尼比的影響在所有的作用力中占據主導地位，對POGO振動的影響很大，貯箱、直管、泵、處產生的作用力對POGO振動幾乎沒有影響。

由此，可通過只考慮推進劑在推力室處產生的作用力，不考慮其他部件處產生的作用力來簡化液體捆綁火箭動力學模型。為進一步驗證這一結論，在頻域仿真中只考慮推力室處作用力的模型，將得到的系統阻尼比與考慮所有作用力得到的系統阻尼比作比較，結果如圖8所示。

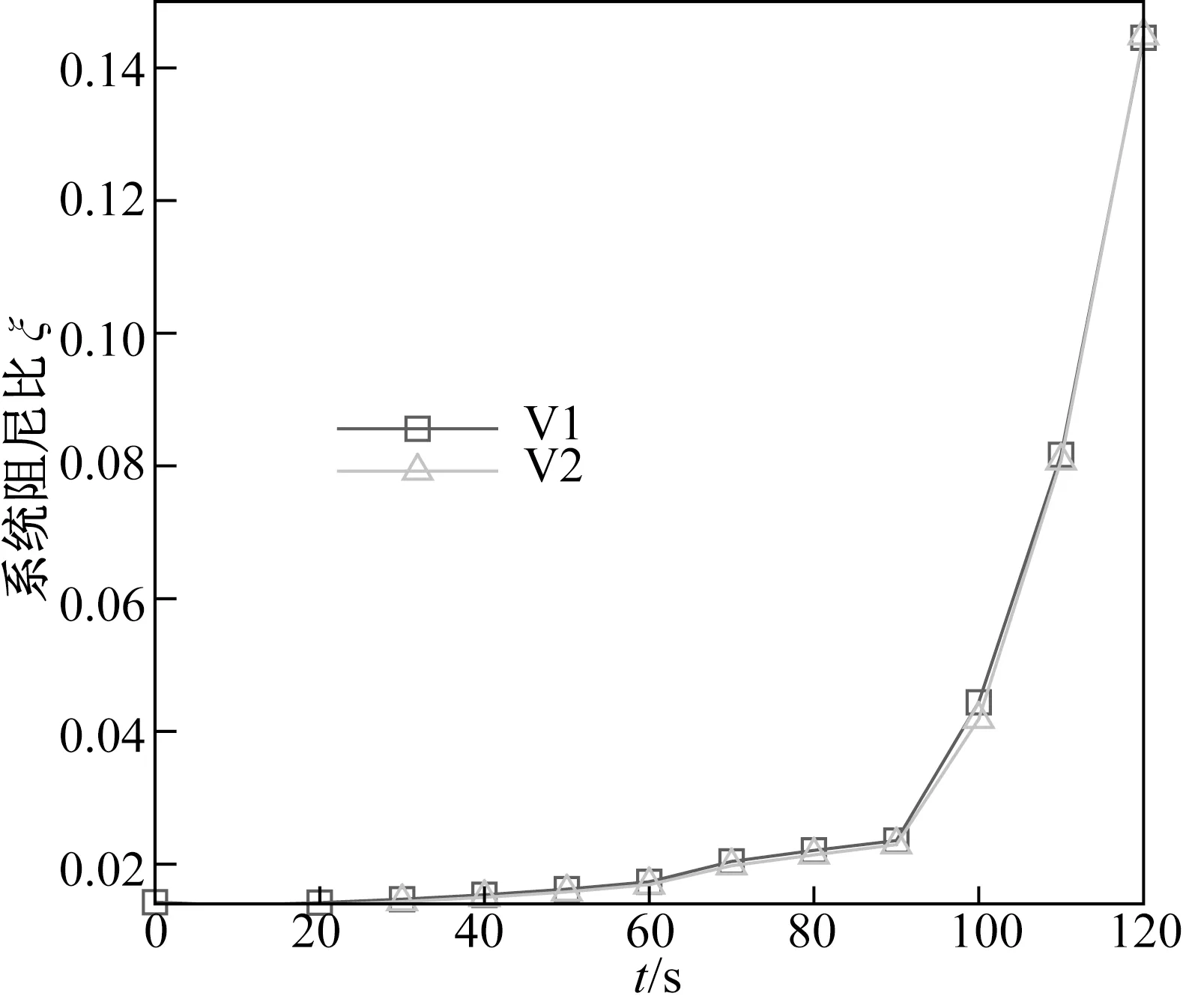
圖8 系統阻尼比對比結果Fig.8 Contrast result of system damping ratio

圖中：V1為考慮了所有外力的系統阻尼比隨時間的變化曲線；V2為只考慮推力室處的外力的系統阻尼比隨時間的變化曲線。兩者之間，系統阻尼比的最大偏差為5.7%。由圖8可知：這2條曲線幾乎重合，故簡化模型可較好地模擬推進系統的特性。這也證明了在推力室處產生的作用力對系統阻尼比的影響在所有的作用力中占據主導地位，對POGO振動的影響最大，貯箱、直管、泵產生的作用力對POGO振動幾乎沒有影響。

4 結束語

搭建并分析雙組元液體捆綁火箭動力學仿真模型，可得以下結論：

1) 在助推段和芯級中，蓄壓器設置在氧路對POGO振動的抑制效果比安裝在燃料路時要好；

2) 蓄壓器設置在芯級氧路和助推段氧路對POGO振動的抑制效果最好；

3) 推力室處產生的作用力對POGO振動的影響在所有的作用力中占據主導地位；

4) 可通過只考慮在推力室處產生的作用力，不考慮其他部件處產生的作用力,簡化液體捆綁火箭動力學模型。

后續研究將集中于POGO振動系統的時域仿真，進一步提高POGO振動系統的穩定性。