一種基于高階Markov使用模型的測試用例自動生成方法

趙衛東 李有俊 張麗

關鍵詞： 高階馬爾可夫使用模型; 快速輪盤賭; 二分查找; 相對熵; 軟件測試; 測試用例自動生成

中圖分類號： TN911.23?34 ? ? ? ? ? ? ? ? ? ? 文獻標識碼： A ? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2019）06?0026?04

Abstract： In order to solve the problem that the test case generation based on the pure Markov usage model is unstable and the test adequacy judgment is inaccurate， an improved high?order Markov test model is proposed on the basis of analyzing the existing test case automatic generation methods. According to this model， an improved test case generation method based on the binary search of the fast roulette， and a test adequacy judgment method based on the relative entropy are put forward. The practical results show that in comparison with the original methods， the improved method can effectively improve the generation stability of test cases and the judgment accuracy of test adequacy， which is suitable for large?scale software testing， and improves the efficiency of large?scale software automatic testing.

Keywords： high?order Markov usage model; fast roulette; binary search; relative entropy; software testing; test case automatic generation

0 ?引 ?言

馬爾可夫（Markov）鏈是根據馬爾可夫性得到的一種隨機過程模型。馬爾可夫性主要體現在其無后效性，即后發生的狀態只跟當前狀態有關，與過去狀態的發生無關。用MarKov鏈描述軟件的真實運行過程即為Markov使用模型。由于Markov使用模型能夠有效地描述軟件的真實運行過程，近年來，基于Markov使用模型的軟件測試技術是軟件測試領域研究的熱點之一。

Tetsuro Katayama等人將基于Markov模型的軟件測試研究擴展到分布式系統上，就如何減少系統延遲進行了深入討論[1]。文獻[2]針對模型建立了一個可視化的測試系統。M.Senne等人則構建了一個基于Markov鏈的軟件分析系統，即EMMA系統。在國內，夏威[3]曾研究過基于Markov模型的可靠性測試用例生成技術;劉洋等研究過基于層次結構Markov鏈的軟件可靠性建模方法，提出了一種基于層次結構的使用模型的構建方法[4];雷航也提出過嚴格Markov模型的軟件可靠性測試方法[5];陳麗敏曾提出改進的二階Markov測試模型[6]。上述測試方法，要么是依賴經驗值來生成測試用例，要么只考慮前一狀態對當前狀態的影響，生成的測試用例存在一定的不穩定性，即生成的測試用例有時不能覆蓋所有的運行狀態。且在生成測試用例時大都依賴大數定律，容易出現“測試用例爆炸”的情況。因此有必要研究并提出一種改進的方法來解決已有測試用例生成不穩定和測試用例數目爆炸的問題。

1 ?基于單純Markov鏈的測試用例生成方法

單純Markov測試方法是基于UML設計模型（用例圖、場景圖以及序列圖）的。由UML模型生成Markov使用模型，然后對Markov使用模型執行單純馬爾可夫測試方法，生成測試用例和Markov測試模型，通過計算使用模型和測試模型的歐氏距離，判斷是否達到一定的測試充分性，直到滿足一定的測試充分性才停止測試[6]。其具體流程如圖1所示。

2 ?改進的馬爾可夫測試方法

本文采用高階馬爾可夫模型對原有模型進行改進，借鑒趙愛華、吳彩華、徐錫山，Razib Hayat Khan等人由UML圖（用例圖、場景圖以及序列圖）生成Markov模型的方法[7?9]，生成Markov使用模型，提出基于高階Markov測試模型的二分查找的快速輪盤賭選擇算法，并應用相對熵代替歐幾里得距離來作為充分性判定條件，從根本上來提高測試用例生成的穩定性和測試結果判定的充分性。同時解決了復雜軟件在進行測試時的測試用例爆炸現象，使其更適合大規模軟件的測試。

2.1 ?高階馬爾可夫使用模型的引入

由于當前狀態很有可能受前面狀態的影響，所以引入馬爾可夫的階。[n]階表示當前狀態受其前n個可達狀態的影響。為解決單純馬爾可夫測試方法的缺陷，在由Markov使用模型生成Markov測試模型時，引入一個中間鏈，考慮n階狀態轉移對當前狀態的影響，重新計算狀態的轉移概率[P（x）]。設[L={L0，L1，L2，…，Ln}]是有限狀態取值集合[E={1，2，…，m}]的一個隨機序列，任意的時間t下，若：

2.4 ?算 ?例

本文以Prowell SJ[11]公開發表在Addison ?Wesley上的衛星嵌入式控制軟件系統（SCS）為例，應用改進的測試用例生成方法和測試充分性判定方法，對衛星嵌入式控制軟件進行測試用例生成試驗，能夠得到測試用例qBA，qBCDEFGHJKL，qBCDEFGHJFGHJKL，qBCDEFGHJFGIJKL和qBCGA數量為3，6，9，3，2時，與之前的測試用例生成的結果相比較，其生成的測試用例數目減少11.54%，且能夠覆蓋所有的測試情況，提高了測試用例的穩定性。

3 ?實驗驗證

本文采用Java語言，應用MyEclipse編程實現上述算法，并以衛星嵌入式控制軟件[11]為例進行測試用例的自動化生成，并對熵值和歐氏距離的偏差值、生成的測試用例數目、覆蓋情況進行統計。

3.1 ?測試用例生成數據比較

根據Markov使用模型，設置閾值，進行試驗，對停止準則及測試用例生成個數，和生成時間進行統計，本次試驗采用進行10次試驗求平均值的方法計算求得。其測試結果如表1所示。

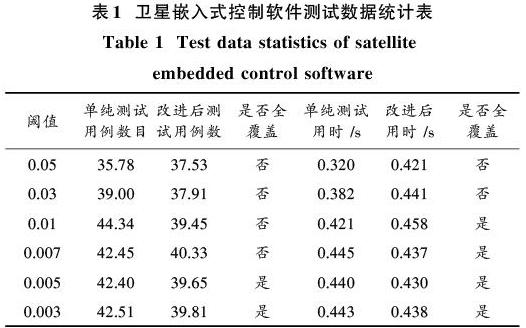
可以看到，由于隨機生成的原因，當采用單純馬爾可夫測試方法時，閾值越小需要生成的測試用例數目越多，最后趨于穩定。從實驗數據可以看出當閾值取值為0.005時，不論從測試時間還是測試用例的數目，都是比較合理的取值。除此之外，從測試結果還可以看到，單純馬爾可夫測試方法可能存在測試覆蓋不全的問題，測試不穩定。改進后的高階馬爾可夫測試方法閾值越小時與單純馬爾可夫方法相比，用時上基本一樣，但是生成的測試用例的數目卻大大減少，特別是針對較大型的軟件，測試用例減少較明顯，且都能夠覆蓋所有路徑，測試更穩定。

3.2 ?充分性判定準則比較

考慮到歐氏距離與熵值都是計算模型的偏差來對模型的充分性進行評判的，且歐氏距離的區分度不如熵值的計算準確。針對上述Markov測試模型，采用反證法，設置閾值為0.005，并統計在得到不同測試用例數目時的相對熵和歐氏距離的偏差。由于，相對熵的計算在計算每個狀態時都乘上了一個平穩分布值，為了保持歐氏距離跟熵值在同一數量級上進行比較，對歐氏距離進行適當的縮放。

從圖2的結果可以看出，相對熵能更加精確地表示兩個模型的偏差。當測試用例的數目逐漸增多時，歐氏距離與熵值的計算結果都快速下降，最后都到達一個相對穩定的值，但相對熵值略大于歐氏距離。所以，當反過來將相對熵作為判斷條件時，可以更加充分地進行判斷是否到達停止條件。

4 ?結 ?語

本文算法有效地提高了測試用例生成的穩定性和測試充分性判定的準確性，解決了大規模軟件測試用例爆炸的情況。但還沒有真正地達到解放手工的要求，以后將致力于應用改進的算法開發一款測試用例自動生成工具，使其能夠自動地生成測試用例并對軟件進行測試，真正實現測試自動化。

參考文獻

[1] KATAYAMA T， ZHAO Z， KITA Y， et al. Proposal of a method to build Markov chain usage model from UML diagrams for communication delay testing in distributed systems [J]. Journal of robotics networking & artificial life， 2014， 1（2）： 120?124.

[2] MCGREGOR S， BUCKINGHAM H， DIETTERICH T G， et al. Facilitating testing and debugging of Markov decision processes with interactive visualization [C]// Proceedings of Symposium on Visual Languages and Human?Centric Computing. Atlanta： IEEE， 2015： 53?61.

[3] 夏威.基于Markov模型的可靠性測試用例生成技術研究[D].杭州：杭州電子科技大學，2016.

XIA Wei. Research on reliability test case generation based on Markov model [D]. Hangzhou： Hangzhou Dianzi University， 2016.

[4] 劉洋，于磊，徐煒珊，等.基于層次結構Markov鏈的軟件可靠性建模方法[J].信息工程大學學報，2015，16（4）：477?482.

LIU Yang， YU Lei， XU Weishan， et al. Software reliability modeling based on hierarchical structure of Markov chain [J]. Journal of Information Engineering University， 2015， 16（4）： 477?482.

[5] 雷航，馬成功.Markov模型的軟件可靠性測試充分性問題的研究[J].電子科技大學學報，2010，39（1）：101?105.

LEI Hang， MA Chenggong. Testing adequacy of software reliability in Markov model [J]. Journal of University of Electronic Science and Technology of China， 2010， 39（1）： 101?105.

[6] 陳麗敏.基于馬爾可夫鏈模型的軟件可靠性測試方法研究[D].成都：電子科技大學，2010.

CHEN Limin. Research on software reliability testing method based on Markov chain model [D]. Chengdu： University of Electronic Science and Technology of China， 2010.

[7] 吳彩華，劉俊濤，彭世蕤，等.基于UML的軟件Markov鏈使用模型的構建[J].計算機研究與發展，2012，49（8）：1811?1819.

WU Caihua， LIU Juntao， PENG Shirui， et al. Deriving Markov chain usage model from UML model [J]. Journal of computer research and development， 2012， 49（8）： 1811?1819.

[8] 趙愛華.基于UML模型的軟件使用模型生成技術研究與實現[D].北京：北京交通大學，2017.

ZHAO Aihua. Research and implementation of software usage model generation technology based on UML model [D]. Beijing： Beijing Jiaotong University， 2017.

[9] KHAN R H， HEEGAARD P E. Translation from UML to Markov model： a performance modeling framework [M]. Dordrecht： Springer， 2010.

[10] 李俊海.高階Markov鏈轉移概率規律一種新表示法[J].應用數學，2015，28（1）：158?164.

LI Junhai. A representation for transition probability of high?order Markov chain [J]. Mathematica applicata， 2015， 28（1）： 158?164.

[11] PROWELL S J， TRAMMELL C J， LINGER R C， et al. Cleanroom software engineering： technology and process [M]. New York： McGraw Hill， 1998.

[12] PROWELL S J. TML： a description language for Markov chain usage models [J]. Information and software technology， 2000， 42（12）： 835?844.