皮下脂肪組織本構模型及其生物力學性能研究進展

崔世海，段海彤，李海巖，賀麗娟，呂文樂，阮世捷

（天津科技大學 機械工程學院，天津 300222）

在汽車安全領域，汽車碰撞安全法規中采用的乘員碰撞損傷準則及乘員保護裝置主要是基于50百分位假人模型制定的，由于肥胖乘員體型的不同，現有基于標準體型的乘員損傷準則和保護裝置是否適合肥胖乘員是值得探討的問題。目前尚未開發出肥胖系列假人，相關尸體試驗也十分匱乏，而有限元模型在研究肥胖乘員損傷機理方面有著獨到的優勢，有限元模型不僅可以顯示碰撞過程中的力學響應情況，而且更易于控制變量，可將混淆的影響因素獨立開來，便于探究肥胖乘員的損傷機理。對于肥胖人體有限元模型而言，其增加的大量皮下脂肪組織是影響其力學響應及損傷機理的重要因素，因此皮下脂肪材料本構模型的選擇及參數的確定是決定其有限元模型生物仿真度的關鍵因素。

脂肪組織占人體總質量的5%～60%，代表新陳代謝相關組織中最具可塑性的組織[1-2]。皮下脂肪組織是一種位于真皮與腱膜和肌肉筋膜之間的結締組織，與真皮結合牢固，其在吸收與分配機械載荷中起著重要的作用，可以吸收沖擊和防止局部應力集中。關于脂肪組織力學性能的研究一直相對較少，且其中大量研究集中于乳腺脂肪組織[3-5]和腳后跟脂肪組織[6-9]，SAMANI 等[10-12]使用不同的本構模型對乳腺脂肪組織進行研究，發現正常乳腺脂肪組織的平均彈性模量在3.25 ～3.6 kPa 之間。MILLER-YOUNG 等[13]使用二階Mooney-Rivlin 本構模型確定了腳后跟脂肪墊的初始剪切模量約為0.02 kPa。ERDEMIR 等[14]采用一階Ogden 模型對腳后跟脂肪墊進行研究，提出初始剪切模量為56 kPa。WEARING 等[15]的體內試驗研究指出，腳后跟脂肪的割線模量為580±145 kPa。有關皮下脂肪組織的研究一直比較匱乏，且主要以壓縮試驗為主，拉伸及剪切試驗[36]相對較少，這是由于脂肪組織十分柔軟，在進行拉伸、剪切試驗時不易固定，而無約束壓縮試驗條件簡單，成功率高。國內一直缺少對皮下脂肪組織力學性能的研究，在不同的有關脂肪組織力學性能研究的文獻中，給出的材料參數具有較大的差異。這些差異可能由樣本、試驗條件以及計算方法的不同而引起。在有限元分析方面，很少有針對脂肪組織力學性能研究的仿真試驗，且在人體有限元模型中采用的脂肪組織材料參數及本構模型均具有較大差異。基于以上問題，本文對皮下脂肪組織的本構模型及其力學性能研究進展進行了綜述。

1 脂肪組織力學試驗

1.1 壓痕試驗

ZHENG 等[16]對8 名志愿者4 個部位的肢體軟組織以3 種身體姿勢進行測試，采用手動壓痕儀評估了下肢軟組織的準線性粘彈性特性。從壓痕試驗中提取數據，對準線性粘彈性本構模型進行擬合。給出初始模量范圍為0.22 ～58.4 kPa，非線性因子范圍為21.7 ～547 kPa，時間常數范圍為0.05 ～8.93 s，材料常數范圍為0.029 ～0.277。研究顯示，不同受試志愿者、不同部位以及不同姿勢等會導致脂肪材料參數發生很大的變化，這可能是由于志愿者間存在個體差異，不同部位脂肪組織分布不同，以及不同姿勢會使肌肉收縮程度不同。

GEFEN 等[20]從20 只5 ～6 個月大的綿羊身上采集了20 組直徑60 mm、厚45 mm 的脂肪樣本，對綿羊的白脂肪組織進行了壓痕試驗，得到了綿羊臀部脂肪組織的彈性模量值。相比其它研究而言，該研究中壓痕試驗的樣本尺寸更大，加載速度更高，但研究中只給出了壓縮至4 mm 時的接觸力，未給出0 ～4 mm 之間的接觸力值。

SIMS 等[26]基于豬皮下脂肪樣本的離體壓痕試驗，通過使用核磁共振成像（MRI）和反向有限元法獲得了脂肪組織的超彈性和粘彈性參數，認為在低、中應變下Neo-Hookean 模型足以模擬壓縮載荷下皮下脂肪的力學響應，并求得了代表彈性變形的初始剪切模量μ為0.53±0.31 kPa，代表粘彈性響應的單項Prony 級數的常數α為0.39±0.03，τ為700±255 s。同時在壓痕試驗中觀測到皮下脂肪組織樣本在卸載后具有不可恢復的變形，認為脂肪組織具有彈塑性，這與PATEL 等[17]的研究結論相一致，與GEERLIGS 等[17]的研究結果相反。該研究中未注明試驗樣本的具體尺寸，Neo- Hookean 單參數模型最簡單，但只適用于模擬低、中等應變情況下的彈性變形，在大應變下該模型缺乏非線性度[30]。

1.2 拉伸與壓縮試驗

WU 等[18]提出了一種新的軟組織研究方法，在測試中不需要將皮膚與皮下脂肪組織分離，從而提高了可靠性并減少了測量誤差。該研究采用8 個不同皮膚與皮下脂肪厚度比的豬前爪軟組織進行無約束壓縮測試，將獲取的豬皮下脂肪組織力學響應結果與MILLER-YOUNG 等[11]公布的數據相比較，結果發現在大應變下，豬皮下脂肪組織的應力大約是人類腳后跟脂肪墊的5 倍，反映了豬前爪脂肪組織與人類腳后跟脂肪墊組織力學性能的差異。該研究首次量化對比了豬前爪脂肪組織與人腳后跟脂肪墊力學性能上的具體差異，為采用豬皮下脂肪代替人體皮下脂肪研究人體脂肪組織力學性能及材料參數帶來的差異提供了一定的參考。

COMLEY 等[21-23]基于豬的皮下脂肪組織進行大范圍應變率（10-4～5 000 s-1）的力學性能試驗。低應變率試驗樣本直徑為10 mm，厚度為8 mm，中、高應變率試驗樣本直徑為10 mm，厚度為3 mm。采用霍普金森壓桿（SHPB）裝置進行脂肪組織的高應變率（1 000 ～5 700 s-1）單軸壓縮試驗。根據準靜態條件下應變為25%的拉伸壓縮循環加載試驗結果，提出脂肪組織在拉伸壓縮時具有對稱的力學響應。該研究發現在準靜態到高應變率的應變率范圍內，應力的大小隨應變率增加而增加，但應力-應變曲線的形狀是不變的，僅其彈性模量的縮放因子有所不同。同時，當應變率低于10 s-1時，脂肪組織對應變率響應不靈敏，彈性模量值約1 kPa。通過對比Ogden 本構模型曲線與3 組典型的脂肪組織應力-應變曲線，指出Ogden 應變能密度模型可以充分描述各個應變率試驗中的數據。根據脂肪組織表現出的不可壓縮性與非線性行為，該研究認為在任何給定的應變率下，單項Ogden 本構模型都能夠體現脂肪組織的應力-應變關系。基于試驗數據擬合得到Ogden系數范圍為20～23，給出0～5 700 s-1內脂肪組織的剪切模量。此外，該研究還提出脂肪組織密度為920 kg/m3，體積模量為0.5 GPa，這與SARAF 等[24]在動態載荷下所測量的人體胃、心臟、肝、肺等軟組織體積模量結果相一致。

隨后，COMLEY 等[25]對脂肪組織微觀結構進行了研究，建立了一個脂肪組織彈性模量的微觀力學模型。利用電子掃描顯微鏡對脂肪組織細胞微觀結構進行觀察，測得脂肪細胞密度與膠原小葉間隔相對密度分別為0.1 與3×10-4。指出脂肪組織的模量由脂肪細胞周圍的膠原網格決定，在37 ℃下可將其理想化為不可壓縮的無粘性流體。提出低應變率下脂肪組織的彈性模量約為1 kPa。通過試驗并參考相關研究，認為增強基底膜在宏觀模量中占主導地位，整體有效模量由增強基底膜和隔膜纖維的模量累加，進而建立了一個脂肪組織彈性模量的微觀力學模型，用以確定微觀結構與宏觀模量之間的關系。該研究基于微觀結構，從生物解剖學角度闡述了脂肪組織表現出的幾乎不可壓縮性，并構建了微觀力學模型。

ALKHOULI 等[29]研究并比較了具有不同生理功能的人體皮下脂肪組織與網膜組織的力學性能。脂肪樣本來自于44 名接受手術的患者，長8 ～17 mm，寬3 ～6.5 mm，厚度1.5 ～3.5 mm，測得拉伸與應力松弛試驗數據，并提出當應變高于30%時脂肪組織出現撕裂的風險很高。在人體脂肪組織的拉伸試驗中觀測到的非線性應力-應變行為與COMLEY 等[19,21,28]及GEFEN 等[18]的研究結果類似。該研究基于人體皮下脂肪，對脂肪組織損傷容限的確定具有極大參考價值。

CALVO-GALLEGO 等[33]采用單軸壓縮應力松弛試驗，研究了人體腹部脂肪組織的粘彈性力學性能。使用準線性粘彈性模型和內部變量粘彈性模型來擬合試驗數據，每一個粘彈性模型都分別用4 種不同的超彈性應變能密度函數表征彈性響應，5 項多項式函數、一階Ogden 函數、各向同性Gasser-Ogden-Holzapfel 函數以及Neo-Hookean 與指數函數的組合，提出內部變量粘彈性模型與Ogden 函數是擬合試驗數據的最佳組合。在模擬脂肪組織的本構模型中，CHAGNON 等[35]的研究指出Neo-Hookean 模型適用于小應變。

1.3 剪切試驗

PATEL 等[17]基于流變剪切試驗與恢復試驗，對人體腹部脂肪組織力學性能進行了研究，該研究樣本來自女性腹部真皮組織下方2 ～4 mm。通過流變試驗測量脂肪組織的粘度、彈性模量和粘性模量，發現脂肪組織隨剪切速率增大粘度不斷降低，呈現剪切稀化特性。利用壓痕儀在不同應變率下測量脂肪組織變形的可恢復性能，發現即使在脂肪組織發生最小的變形卸載后，其變形也不能恢復。此外，在加載力不斷增大時脂肪組織會發生失效損壞。

GEERLIGS 等[19]測量和描述了皮下脂肪組織小應變情況下的線性粘彈性行為。利用豬背部中層皮下脂肪組織進行剪切試驗，樣本直徑為8 mm，厚度為1.5 ～2 mm。研究發現在線性粘彈性狀態下，0.1%應變內，儲能模量與耗能模量對頻率及溫度具有依賴性行為，且在37℃時10 rad/s 加載下脂肪組織剪切模量為7.5 kPa，并引入冪函數模型來描述恒溫下的脂肪組織頻率相關行為與應力松弛行為。該研究還分析了脂肪樣本快速冷凍保存方法的效果，指出組織學檢查顯示冷凍后可能出現組織損傷，但機械性質沒有改變。而后GEERLIGS 等[27]基于剪切試驗，研究了白脂肪的觸變性和抗觸變性，并提出如果樣本卸載后給予足夠的恢復時間，其能夠完全恢復形變。

SOMMER 等[34]首次通過雙軸拉伸和三軸剪切試驗對人體腹部脂肪組織進行力學性能研究，并采用超彈性模型表征準靜態下脂肪組織的多軸力學行為。提出在準靜態和動態多軸加載下的人體腹部脂肪組織表現為非線性、各向異性的粘彈性軟生物材料，認為在組織學研究中觀察到的膠原隔膜導致了組織的各向異性。

2 脂肪組織本構模型

2.1 線性粘彈性材料本構

該材料模型由一個彈性元件與Maxwell 模型并聯而成，常用于模擬人體軟組織，包括肌肉、脂肪、心臟、肺等。線性粘彈性材料本構模型中，假定偏應力張量具有線性粘彈性特性。

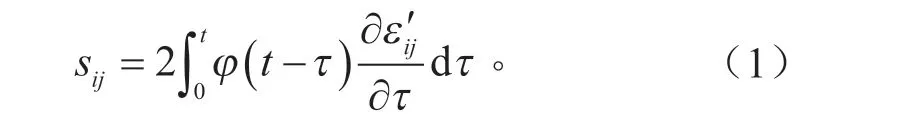
式中：sij為應力偏量速率；為應變率偏量。由體積彈性模量與剪切松弛模量定義力學特性，其中剪切松弛行為由式（2）表示：

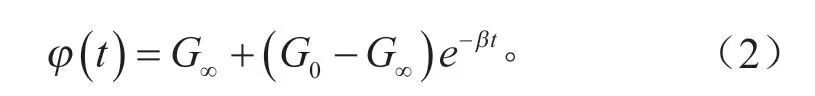
式中：G0為短效剪切模量；G∞為長效剪切模量；β為衰減常數。用遞歸公式從tn時刻計算tn+1時刻的遺傳積分新值。體積彈性行為假定為：

式中：p為壓力，逐步積分累加。

2.2 Mooney-Rivlin 超彈性材料本構

該材料模型最初是為了模擬橡膠材料的大變形而開發的，后經變形已經成功用于生物力學研究，用來模擬各種軟組織，包括腦組織、血管組織和腳后跟脂肪墊等，還可用來表征具有不可壓縮、大變形的材料。Mooney-Rivlin 材料模型基于應變能密度函數，其方程式為：

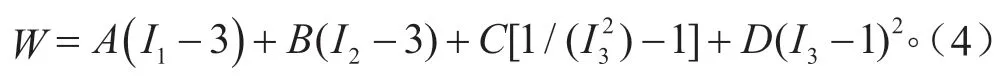
式中：C、D可由A、B、ν表示：

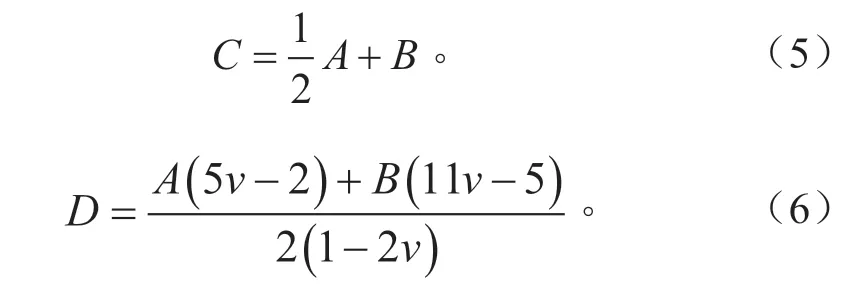
式中：W為應變能；A、B為Mooney-Rivlin 材料常數；I1、I2、I3分別為右柯西-格林應變張量；ν為泊松比，該方程假定組織是各向同性和不可壓縮的，即I3=1。通過應變能函數相對于柯西-格林應變張量的偏導數得到第二皮奧拉-克希霍夫應力：

式中：Sij為第二皮奧拉-克希霍夫應力；Eij為柯西-格林應變張量。

2.3 Ogden 超彈性材料本構

Ogden 材料本構模型是接近不可壓縮的超彈性模型，許多研究表明，該材料本構模型在模擬脂肪組織力學性能上表現良好，其應變能密度函數為：

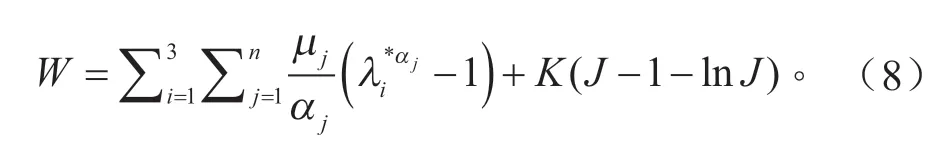
式中：μ為剪切模量；α為Ogden 系數；K為體積模量；J為相對體積。

該模型中粘彈性響應表達形式為：

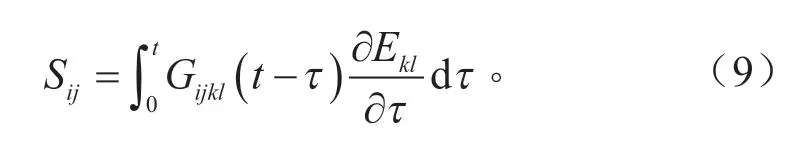
式中：Gijkl為松弛函數。將該粘彈性應力加到由應變能密度函數得到的應力中，考慮脂肪組織的應變率依賴性，引入Prony 級數中的6 個項表示松弛函數，實際上是由阻尼器和彈簧串聯組成的Maxwell模型，其方程為：

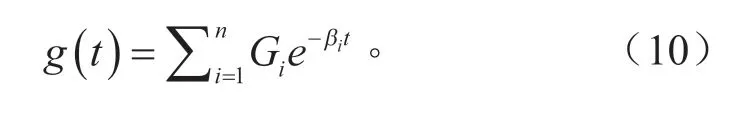
式中：Gi為剪切模量；βi為衰減常數。

2.4 軟組織材料本構

該材料本構是一種代表生物軟組織的橫向各向同性超彈性模型，如韌帶、肌腱和筋膜等。在該模型的粘彈性選項下，會引入一個6 項的Prony 級數作為松弛函數。在這種情況下，超彈性應變能代表彈性響應。整體應變能W是“解耦的”，包括兩個各向同性偏矩陣項：

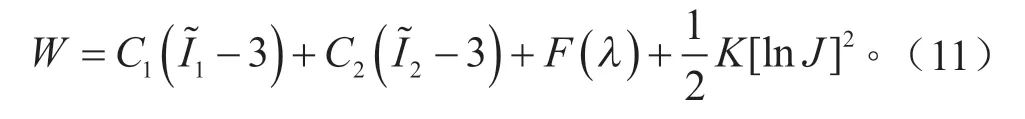
式中：I(1~與I2~為右柯西變形張量的偏量；λ為沿當前纖維方向的拉伸比；J為體積比；C1、C2為Mooney-Rivlin 系數；K為有效體積模量。

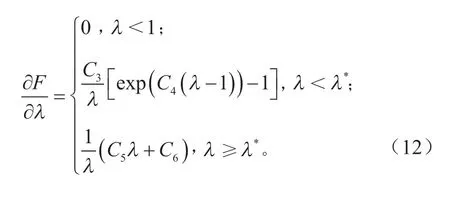
式中：Ci為材料常數。將C3、C4設置為0，并使λ*足夠大，使其表現為各向同性且對稱。粘彈性特征由卷積積分表示時間依賴的第二皮奧拉-克希霍夫應力：

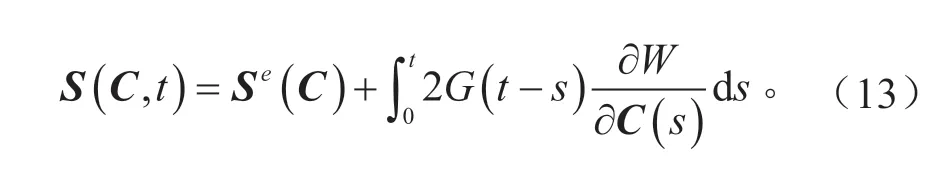
式中：Se為由應變能求導出的第二皮奧拉-克希霍夫應力的彈性部分；G(t-s)為由Prony 級數表示的松弛函數，將Prony 級數引入式（13）得到：

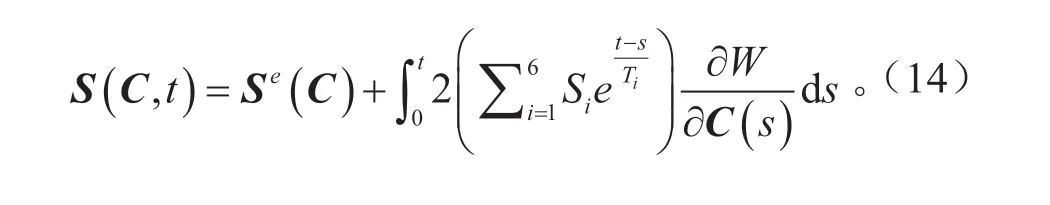
2.5 材料本構模型在有限元分析中的應用研究

表1 脂肪組織力學性能試驗匯總

已有學者對模擬脂肪組織的不同材料本構進行了研究，ENGELBREKTSSON[28]在LS-DYNA 軟件中尋找潛在的可能符合白脂肪組織力學性能的材料本構模型，采用COMLEY 等[21]的研究中的脂肪組織在不同應變率范圍的應力-應變試驗數據，對Ogden、Simplified Rubber、Soft Tissue 等材料本構模型進行校核。仿真結果與試驗數據的對比表明，Ogden 模型在低、中應變率下模擬脂肪材料較為合適，簡化橡膠材料模型在低應變率下表現良好，軟組織材料模型在模擬脂肪的非線性特性中表現較差。但該研究中未給出各個本構模型材料參數的來源，沒有考慮材料參數調整對仿真最終結果的影響。

MIHAI 等[31]在定性和定量上分析了脂肪組織的力學性能，指出通常用于模擬軟組織的Fung、Gent 模型、Neo-Hookean 和Mooney-Rivlin 模型不適用于模擬在拉伸和剪切下的脂肪組織，其中Ogden超彈性模型模擬結果與試驗吻合良好，適用于在有限元分析中模擬脂肪組織。表1 總結了以往文獻中對脂肪組織力學性能的研究情況。

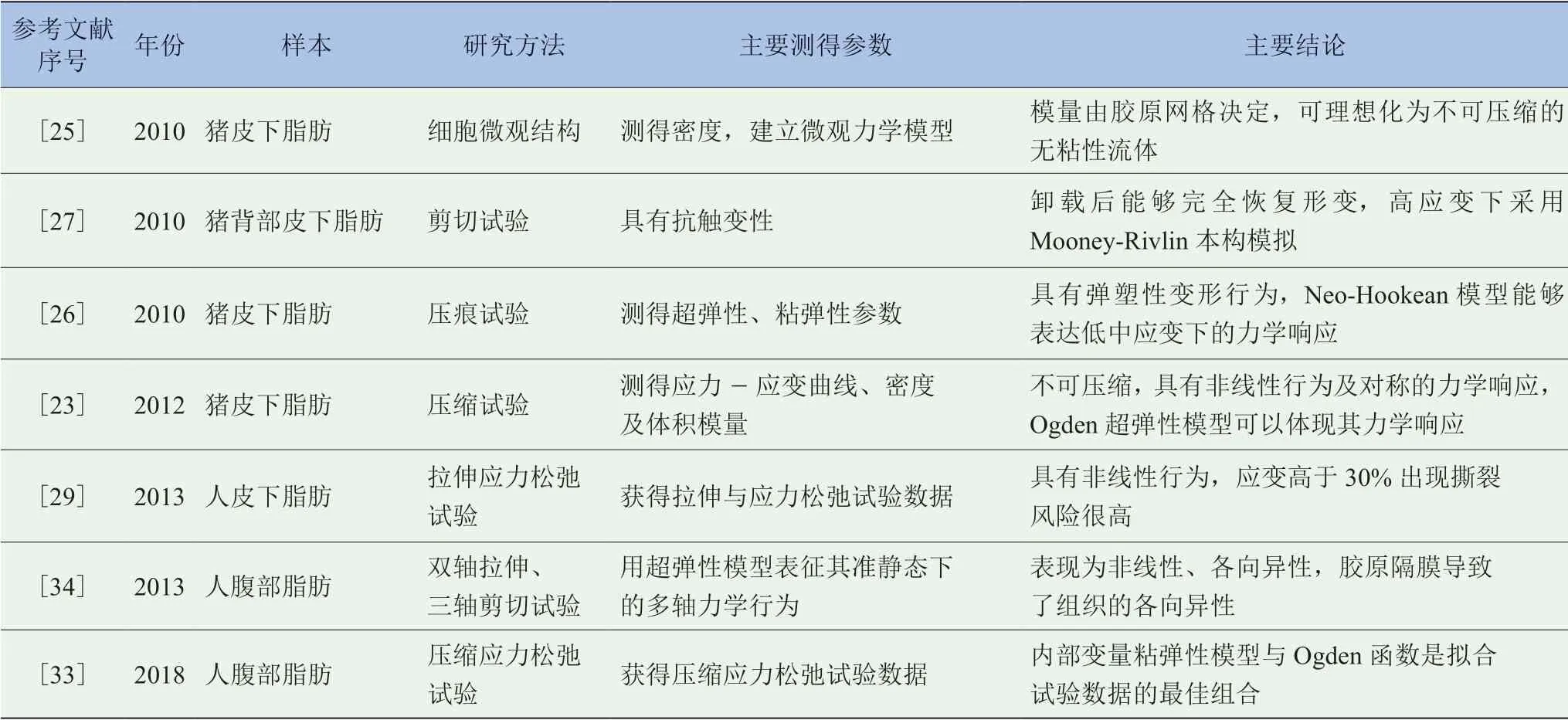
續表1：

3 結語與展望

通過對脂肪組織力學性能研究的分析與總結（表1），為脂肪組織力學性能的進一步研究，及其在有限元建模及分析上的應用提供參考和幫助。通過回顧并總結以往國內外學者對脂肪組織進行的力學性能試驗及相關研究成果，可得到以下結論：

（1）目前，歸納分析以往研究，認為脂肪組織是各向同性的，拉伸及壓縮具有對稱性的，并具有非線性力學響應及應變率依賴特性的不可壓縮性軟組織。

（2）Ogden 超彈性材料本構能夠較好地模擬脂肪組織的力學響應特性。

（3）脂肪組織的損傷閾值可暫定為應變為30%。

不難發現，與肌肉、腦組織等軟組織相比，脂肪組織力學性能的研究還遠遠不夠。同時，已有研究中對脂肪組織力學性能的描述存在諸多爭議，不同文獻中往往得到的研究結果不一致，而引起這些差異的因素可能是多方面的，包括樣本的尺寸及來源，試驗前樣本的預處理程序及方法，不同的試驗方法等，這些不確定性因素都有可能導致研究結果上的差異。今后開展脂肪組織力學性能研究可從以下幾個方面進行：

（1）開展脂肪組織力學試驗，基于試驗數據，運用有限元仿真與優化策略相結合的方法，反求獲取具有更高生物仿真度的材料參數。

（2）數字圖像相關技術（DIC）屬于非接觸式測量，其對測量環境要求較低，可測量全場變形，嘗試引進數字圖像相關技術研究脂肪組織力學性能。

（3）目前不同生物、不同部位引起的脂肪組織力學響應差異仍然未知，應著手對不同生物樣本和不同部位的脂肪組織給力學響應帶來的不確定性進行研究。