基于相干度優化的極化順軌干涉SAR慢小目標CFAR檢測

張鵬， 張嘉峰， 劉濤，*

(1. 海軍工程大學電子工程學院, 武漢 430033； 2. 海軍作戰支援艦第二支隊， 舟山 316000)

地面運動目標檢測(Ground Moving Target Indication,GMTI)是合成孔徑雷達(Synthetic Aperture Radar,SAR)遙感領域重要的研究分支[1]。近年來，隨著SAR順軌干涉(Along-Track Interferometry,ATI) 理論的逐步完善，基于干涉圖的GMTI方法因其具有對慢速運動目標的檢測能力而備受關注[2-4]。但現有的、包括干涉圖在內的SAR GMTI方法在對慢速運動目標尤其是淹沒在背景雜波內的慢動小目標進行檢測時，仍存在虛警概率與漏檢概率高的問題，且最小可檢測速度往往高于預期的結果。在經典雷達極化中，全極化雷達已被證明能夠檢測單極化雷達所檢測不到的弱小目標[5-6]，因而利用全極化信息進行GMTI或許是解決上述問題的有效手段[7-10]。

利用全極化SAR(Polarimetric SAR,POLSAR)進行GMTI的研究分為單通道與多通道2類方法。在單通道POLSAR GMTI領域，加拿大學者Liu[11-12]提出利用當前分時極化測量體制POLSAR所獲取的交叉極化項進行干涉處理以提高運動目標檢測性能的方法，并采用CV-580 SAR實測全極化數據證明了交叉極化進行GMTI的潛力，但本質上這種利用了HV與VH極化的互易性的方法仍可看作單極化ATI方法的拓展。對于多通道POLSAR GMTI，文獻[13]指出利用單航過極化干涉SAR進行GMTI是未來極化干涉技術的重要應用，并以可測速區間為優化準則對全極化順軌干涉SAR(AT-POLINSAR，添加前綴“AT-”用以區分極化交軌干涉SAR(POLINSAR))系統進行了優化設計，但該研究立足于現有的分時極化測量SAR，并不適用于未來同時極化測量體制且沒有對新系統進行具體的檢測器設計。文獻[7-10]指出具有精確極化散射特性測量能力的同時極化測量技術是未來乃至相當長一段時期內極化測量體制發展的主流趨勢，因而開展同時測量AT-POLINSAR慢動目標自動檢測算法的研究對POLSAR GMTI理論體系的建立以及AT-POLINSAR系統設計都具有重要的意義。當前可直接用于AT-POLINSAR進行GMTI的算法主要有2類：一是文獻[1]提出的基于多頻段多孔徑極化SAR(MFMA POLSAR)的方法，即通過最優極化干涉理論[14-16]對MFMA POLSAR回波降維后采用雜波對消進行運動目標成像；二是文獻[17]提出的利用對數似然比(Likelihood-Ratio Test,LRT)[18]對目標極化干涉協方差矩陣進行檢測的方法。但這2種方法都難以推導檢測量的統計分布，且依賴于對目標先驗信息的獲取，不宜擴展成恒虛警(Constant False Alarm Rate,CFAR)檢測器。綜上所述，為設計實用的AT-POLINSAR慢動目標自動檢測算法，主要有2方面亟待研究的問題：一是建立POLSAR 順軌干涉的統計建模與參數估計理論，與傳統單極化ATI不同的是，全極化ATI除考慮同一極化通道內的干涉相干度外，還要額外考慮不同極化通道之間的相干度以充分挖掘運動目標與雜波背景之間的差異；二是構造性能較優且解析門限易于求解的檢測量，單極化條件下利用干涉圖幅度和相位聯合CFAR檢測量的檢測性能較優[2-4]，那么如何將這種方法擴展至全極化或者針對極化矢量干涉回波重新構造新的檢測量將是實現慢動目標CFAR檢測的關鍵。

針對上述問題，本文首先對單基線AT-POL-INSAR回波進行建模分析；然后針對其6維極化矢量干涉數據，提出基于背景雜波平均相干度最優的降維新方法，從高維干涉矢量中合成出次優極化標量干涉數據，從而可以將單極化順軌干涉SAR(AT-INSAR)慢動目標檢測算法直接應用到全極化系統進行目標檢測；最后，分別采用蒙特卡羅仿真實驗與場景檢測實驗對次優極化、單極化的慢動目標CFAR檢測進行性能對比。

1 全極化順軌干涉SAR系統

本節基于MFMA POLSAR[1]與分時極化AT-INSAR[13]的設計思路，提出一種設備復雜度相對較低、可實現度高的單基線AT-POLINSAR的新系統。基于對系統工作方式、天線收發模式與信號形式的設計，建立了極化矢量干涉模型, 將SAR單極化順軌干涉擴展成全極化矢量干涉。本節的AT-POLINSAR的信號模型可擴展到MFMA POLINSAR，同時，矢量干涉模型也適用于分時極化測量順軌干涉SAR。

1.1 AT-POLINSAR系統信號與回波建模

圖1為單基線AT-POLINSAR系統的成像幾何示意圖，設雷達平臺在高度為H的直線軌跡以速度vp勻速飛行，沿雷達平臺運動方向配置2副相同的全極化天線分別作為前、后向干涉通道m和s，并在不同的方位采樣時刻同時發射h極化與v極化狀態的正交波形，從而在h、v極化天線之間形成了共同的物理干涉基線2Lb。關于天線工作方式，本文假設2副天線按照“乒乓”模式工作，即2副天線輪流發射全極化信號并同時接收極化回波，相較于全孔徑發射子孔徑接收的方案，這種方式在基線配置、系統實現等方面具有更高的靈活性[19]。

圖1中，β為合成孔徑雷達下視角，Ra為雷達成像斜距，θ為斜視角，Lb為基線長度，vp為平臺運動速度，設雷達平臺運動方向(方位向)為x軸正方向，設地距方向為y軸正方向。在t=0時刻，前向干涉通道m的天線相位中心的坐標為(0,0,H)，后向干涉通道s的天線相位中心的坐標為(-Lb,0,H)，設目標以初始坐標T0(x0,y0,0)作勻速直線運動，其方位向與距離向的速度分量分別為vx、vy。m通道天線發射全極化線性調頻(Linear Frequency Modulation,LFM)信號s=[sh(τ),sv(τ)]T[9-10]，sh(τ)與sv(τ)分別為水平、垂直極化，兩者相互正交，且具有如下的共同形式：

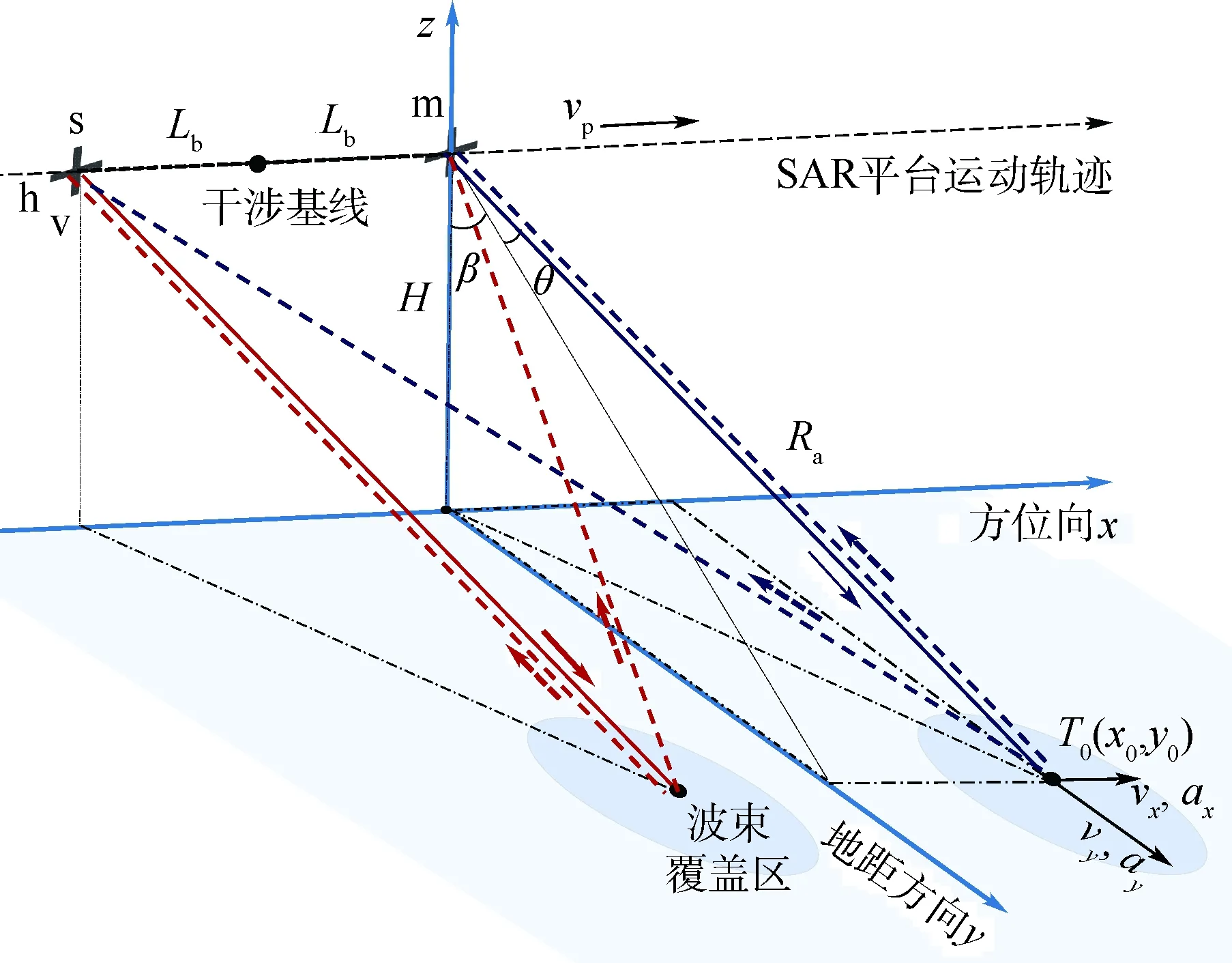
圖1 單基線AT-POLINSAR成像幾何示意圖Fig.1 Geometry schematic diagram of single-baseline AT-POLINSAR acquisition

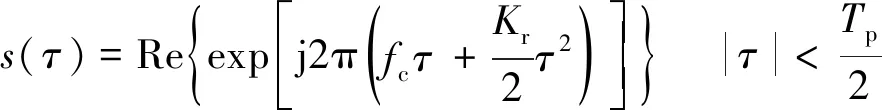
(1)

式中：τ為合成孔徑處理的快時間；fc為發射信號載頻；Kr為線性調頻率；Tp為脈沖寬度；|·|表示取絕對值算；Re{·}表示取實部運算。為討論方便，下文SAR信號處理時不區分極化狀態。發射信號s(τ)目標T0散射后分別由m、s通道的全極化天線進行接收。

sxyi(t,τ)=Axysy(τ-τdi)=

(2)

其中：sxyi(t,τ)表示i通道x極化天線接收到的y極化狀態發射信號的回波，t為慢時間，x,y∈{h,v}，i∈{m,s}，這里h、v表示極化狀態，m、s則表示干涉通道類型；Axy為目標散射系數；τdi為i通道接收到回波的時延，若t時刻目標與m通道和i通道天線相位中心的瞬時斜距分別為RTm(t)與RTi(t)，則τdi=(RTm(t)+RTi(t))/c，c為光速。對i通道回波進行距離壓縮，可以得到

sinc(πKrTr(τ-τdi))

(3)

其中：sinc(·)表示沖激響應函數；Tr為脈沖重復時間；λ為載波波長，對瞬時斜距進行拋物線近似[20]，i通道回波的相位即為

(4)

式中：R0為最短距離[20]，mi的下標i=m或s，mm=0，ms=1。對式(4)的信號進行方位向壓縮，并忽略幅度系數，可以得到目標在目標存在的某一固定距離單元內的復圖像為

(5)

其中：u為方位向像素；ux0為靜止目標方位向像素位置；Δu=ΔX/ΔRx為目標偏移像素數，ΔRx為方位向分辨率，ΔX為方位向偏移距離，且ΔX=(x0vx+y0vy)/vp。再對前后通道各極化回波進行干涉處理可得

(6)

式中：Ixy-xy(u)也被稱為ATI干涉圖；Ta為合成孔徑時間，從式(6)可得目標的干涉相位φi表達式為

(7)

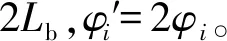
1.2 AT-POLINSAR系統極化矢量干涉模型

(8)

(9)

(10)

(11)

采用R進行表示的優勢在于能夠同時分析極化通道與干涉通道之間的相干度，且二者都能用于區分運動目標與靜止目標。因而，對于單極化SAR ATI來說，以hh極化回波(h極化發射、h極化接收)為例，只需要考慮c11、c33即可。在式(9)的復高斯分布假設下，C將服從復Wishart分布[5-6]：

(12)

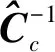
2 極化矢量干涉降維

由第1節的信號模型可知，相較于傳統的極化SAR或干涉SAR，AT-POLINSAR信號處理維度急劇增加，為從其回波中檢測出運動目標并估計運動狀態，需要對高維極化干涉矢量數據進行降維處理，本節在回顧經典的最優極化干涉降維方法的基礎上，提出了一種新的次優極化干涉降維方法。

2.1 經典最優極化干涉降維方法

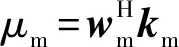
(13)

(14)

對于式(14)需要說明的是，相干度的任意損失都將引起干涉相位差估計精度的下降，因而“信號s1之間的與s2相干度ρ越大，干涉相位φi的估計就越準確”[1]。為獲得最大相干度ρmax，Cloude和Papathanassiou[14]首次提出通過式(15)求解最優權矢量wm與ws的方法：

(15)

通過式(15)，可以求得km與ks的最優加權矢量分別為wm,opt與ws,opt，利用最優權矢量加權得到的新的合成極化狀態μm,opt與μs,opt稱為最優極化，同樣還可得到最優干涉矩陣Jopt，最優干涉圖Iopt以及最優干涉相位φi,opt。

2.2 基于背景雜波平均相干度最優的次優極化干涉降維新方法

傳統的干涉圖模型之所以不再適用于最優極化狀態，是因為極化矢量km和ks最優加權矢量wm,opt與ws,opt是從每一像素單元逐一計算得到的[16]，而這種非線性的加權系數會嚴重影響最優干涉圖的分布類型和分布函數的復雜度。但如果對整副全極化圖像采用統一的線性加權矢量進行降維，分布推導的問題將可得到簡化，但線性加權矢量的選取并不是任意的，其必須滿足一定的準則。本文為對極化數據線性降維處理并使其降維后的雜波背景區域仍然能夠像最優干涉那樣達到較高的相干度，提出了針對背景雜波的次優干涉相干度準則(Suboptimal Interferometric Coherence Principle,SICP)。

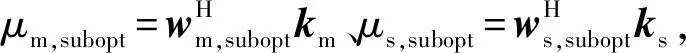
(16)

式中：μ=[μm,suboptμm,subopt]T;θ為潛在的干涉相位，對于靜止雜波背景θ=0，對于運動目標θ與其徑向速度有關。由式(16)，定義雜波背景區域的平均相干度為

(17)

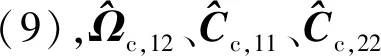
(18)

對其求偏導，得

(19)

(20)

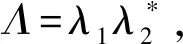
(21)

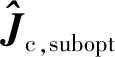
p(ξ)=

(22)

p(ψ-θ)=

(23)

式(22)中：I0(·)與Kn-1(·)分別為第1類和第2類修正的貝塞爾函數，二者的階數分別為0階與n-1階[22]。式(23)中：-π<ψ≤π；2F1為廣義超幾何函數，分布函數的最大取值是ψ=θ，對于靜止雜波背景而言θ=0 rad。對AT-POLINSAR分布式雜波進行仿真，可以得到式(22)和式(23)的理論PDF曲線對實驗數據統計直方圖，擬合效果如圖2(a)和(b)所示，由圖可見單極化干涉圖統計分布理論對次優極化的適用性。文獻[23]對基于干涉圖的自動檢測算法進行了研究，提出了檢測性能較優的利用幅度相位進行聯合檢測的M&P檢測量并推導了檢測量所服從的S分布[見文獻[23]式(6)～ 式(13)]。本文將M&P檢測量應用于次優極化干涉圖幅度、相位并將其命名為次優極化檢測量(SICD)，采用仿真實驗可以得到S分布對次優極化SICD檢測量的統計分布擬合效果如圖2(c)所示。

圖2(a)～(c)所示的擬合效果充分驗證了式(21)結論的正確性，表明次優極化干涉與單極化干涉具有相同的統計分布類型，因而可直接將單極化多通道SAR慢動目標檢測方法應用到次優極化進行慢動目標CFAR檢測。圖2(d)為仿真得到的各單極化狀態、最優極化狀態、次優極化狀態的相干度統計分布，由圖可知，次優極化同樣 能夠達到較高的相干度，從而可以提高分布式雜波背景的相位估計精度。

圖2 次優極化統計分布Fig.2 Statistical distribution of suboptimal polarization

圖3為hh單極化與次優極化的干涉圖在極坐標系下的二維分布散點圖(圖中徑向表示相干度幅度，紫色數字標注)，從圖中也看出上述結論。對比圖3(a)、(b)可以發現,次優干涉圖的雜波分布比較集中，與目標之間的區分度明顯提高，這也是次有干涉準則能夠利用全極化優勢以提高檢測性能的原因。但需要注意的是，由于目標采用了與雜波相同的加權系數，其相干度往往不能達到最優，干涉相位中心也會發生隨機的偏移，目標干涉相干度與相估計中心偏移的方向、大小與雜波特性密切相關，但總的來說，采用這種降維方式可較充分地利用全極化信息以提高運動目標檢測時的信雜比。

圖3 干涉圖二維散布特性Fig.3 2D scatter characteristics of interferograms

3 AT-POLINSAR慢小目標CFAR檢測

3.1 基于SICP的慢小目標CFAR檢測流程

第2節討論了次優極化的統計特性及干涉圖散布特性，結果表明現有單極化AT-INSAR慢動目標CFAR檢測方法亦適用于次優極化，因而采用SICP準則對AT-POLINSAR進行慢動目標檢測的流程可歸納為圖4所示。

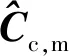
2) 將wm,subopt與ws,subopt分別應用到前后通道的全極化圖像，矢像加權結果作為“次優極化”輸出，即μm,subopt與μs,subopt。

3) 對前后干涉通道應用慢動目標檢測算法進行慢動目標檢測。

3.2 檢測實驗與結果

3.2.1 蒙特卡羅仿真實驗

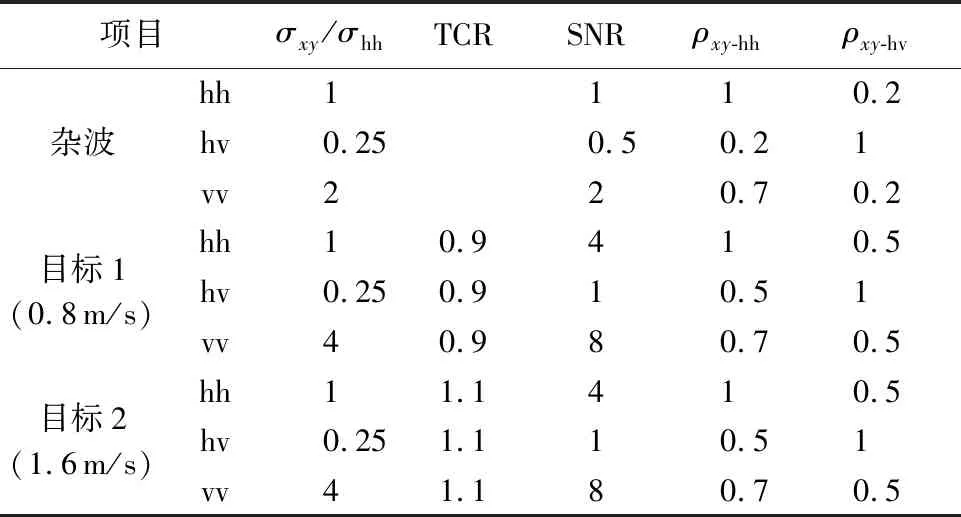
為檢驗次優極化的檢測性能，首先將次優檢測與單極化檢測、全極化LRT方法[17]進行性能對比。采用蒙特卡羅實驗，對文獻[23]中單極化干涉相位檢測器、天線相位中心偏置(DPCA)檢測器、雙曲線檢測器以及M&P檢測器應用到次優極化時的檢測性能接收機工作特性(ROC)曲線進行仿真分析。實驗前首先需要對AT-POLINSAR進行數據仿真，本文借鑒了文獻[24]的數據生成方法對AT-POLINSAR分布式雜波與目標數據進行仿真：即產生6維相互獨立的復高斯分布數據后對其進行二維相關濾波得到服從6維聯合復高斯分布的干涉矢量回波序列。但與文獻[24]不同的是，本文采用特征值分解方法代替Choleskey分解方法進行6維復高斯分布序列的產生，從而降低了對干涉協方差矩陣正定性的要求，只需要滿足半正定即可對分布式目標或雜波的回波數據進行仿真。為使比較更有針對性，數據仿真的關鍵參數參考文獻[17]進行設置，信雜比(Target-to-Clutter Ratio,TCR)、目標運動速度等參數如表1所示，其中雷達平臺運動速度為126 m/s，重復觀測時間為1.6 ms。

表1中，TCR為hh極化狀態下的目標與雜波的RCS之比；信噪比(Signal-to-Noise Ratio，SNR)參數用于計算各單極化狀態下順軌干涉的相干度，即還需手動設置雜波與目標極化相干矩 陣RC,RT(但不是任意地選取)，本文假設目標交叉極化之間的相干度比雜波低，將RC與RT設為

圖4 采用SICP進行運動目標檢測流程圖Fig.4 Flowchart of moving target detection using SICP

項目σxy/σhhTCRSNRρxy-hhρxy-hv雜波hh1110.2hv0.250.50.21vv220.70.2目標1(0.8m/s)hh10.9410.5hv0.250.910.51vv40.980.70.5目標2(1.6m/s)hh11.1410.5hv0.251.110.51vv41.180.70.5

(24)

由上述參數即可對AT-POLINSAR在低TCR條件下的慢動目標和雜波圖像進行仿真，對仿真數據進行4視處理，分別采用次優極化、單極化對目標1、2進行107次的蒙特卡羅檢測試驗，可以得到如圖5所示的ROC曲線。文獻[20]指出，實際應用中對于ROC曲線只需要關注其低虛警區間，如(10-5,10-3)。因而由圖5可得，對于當前2類試驗場景，次優極化檢測性能排序依次為LRT>SICD>DPCA>雙曲線檢測器測器。另外，還能發現全極化信息對每一類檢測器所帶來的檢測性能增益是不同的，但總的來說，各檢測器均能

圖5 ROC曲線仿真結果Fig.5 Simulated curves of ROC

通過次優極化提高檢測概率。

3.2.2 場景檢測實驗

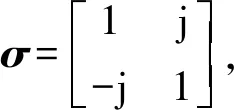
下面進行場景圖像檢測實驗。重新對表2中的4個點目標進行信號級成像仿真，得如圖7(a)所示點目標響應圖像，然后設置TCR=1，得到圖7(e)所示的帶有雜波背景的AT-POLINSAR場景圖像，由圖知，此時所有目標均淹沒于雜波背景中，故傳統單通道幅度檢測已無法對目標進行提取。現首先對AT-POLINSAR場景圖像的hh極化通道應用M&P檢測器，得到圖6(b)所示的檢測量輸出；然后利用SICP方法獲得求解次優極化，并對次優極化應用DPCA、SICD，可以得到如圖7(c)、(d)所示的SICD輸出。經計算，此時M&P(hh極化)、DPCA(次優極化)、SICD對目標2的TCR輸出分別為4.77、13.11、17.16 dB，對目標3的TCR輸出分別為11.25、13.52、17.39 dB。

最后，設置虛警率Pfa=10-4，對圖7(b)～ (d)所示檢測量輸出進行CFAR檢測，可以得到如圖7(f)～(h)所示的檢測結果，對比可見，2次優極化檢測器對目標區域的檢測結果較為完整，且無運動目標漏警發生，而單極化檢測器中檢測性能較優的M&P檢測量則產生了一次漏警，未能檢測出目標2。通過次優極化，AT-POLINSAR不僅能夠提高對低信雜比條件下慢動的目標檢測概率，還可利用全極化信息對檢測出的運動目標進行最優相位估計，對慢動目標的徑向速度進行高精度的估計，從而計算并校正方位向的成像位置偏移，即運動目標成像，如圖7(h)所示。

圖6 場景圖像仿真流程和仿真結果Fig.6 Generated flow and result of simulated scene image

參數數值雷達工作距離/m4000.0載機飛行速度/(m·s-1)276.0波長/m0.1脈沖重復頻率/Hz662.0基線長度/m3.34合成孔徑時間/s0.8696重復觀測時間/s0.0121發射脈沖寬度/μs1.0發射信號帶寬/MHz216.0發射信號中心頻率/GHz3.0過采樣率1.2斜視角/(°)0分辨率(方位/m×距離/m)1.0×1.0分辨率加權因子1.2目標1坐標(距離向/m,方位向/m)(25,0)目標2坐標(距離向/m,方位向/m)(75,0)目標3坐標(距離向/m,方位向/m)(125,0)目標4坐標(距離向/m,方位向/m)(175,0)目標1徑向速度/(m·s-1)0目標2徑向速度/(m·s-1)0.9目標3徑向速度/(m·s-1)-1.2目標4徑向速度/(m·s-1)0

注：成像算法為距離多普勒； 雜波類型為復Wishart。

3.2.3 AT-POLINSAR速度估計精度

采用次優極化方法對目標的徑向運動速度進行估計，需要先對圖像進行GMTI，然后再對檢測結果中心區域重新進行最優干涉處理和徑向速估計，這是由于SICP對均勻圖像背景應用統一的權矢量，會導致目標像素位置處的干涉相位具有一定的偏差。雖然采用這種二次估計的速度估計流程不如單極化情形速度提取的方便，但卻能充分利用全極化信息，圖8為目標徑向速度估計相對誤差曲線，從圖中可見，在各個測試速度點上，利用AT-POLINSAR全極化信息進行相位估計，均能達到最優的徑向速度估計精度(亦可驗證文獻[14]中“干涉相干度越高，相位估計越準確”的結論)。

圖7 AT-POLINSAR信號級仿真圖像和不同檢測算法的檢測結果Fig.7 Signal level simulation image AT-POLINSAR and its detection results by different algorithms

3.2.4 極化干涉協方差矩陣估計點數的選取

背景雜波極化干涉協方差矩陣的估計是SICP處理的重要步驟，協方差矩陣的估計精度會直接影響次優極化干涉相干度及慢動目標CFAR檢測器的檢測性能，如圖9所示。從圖9的不同估計點數下相干度分布和SICD檢測性能ROC曲線結果可以發現，對于常用的4視處理極化順軌干涉SAR圖像，估計點數選擇64即可獲取較高的雜波相干度和慢動目標檢測性能，因而3.2節開展實驗時，SICP處理選用8×8窗口對協方差矩陣進行估計。

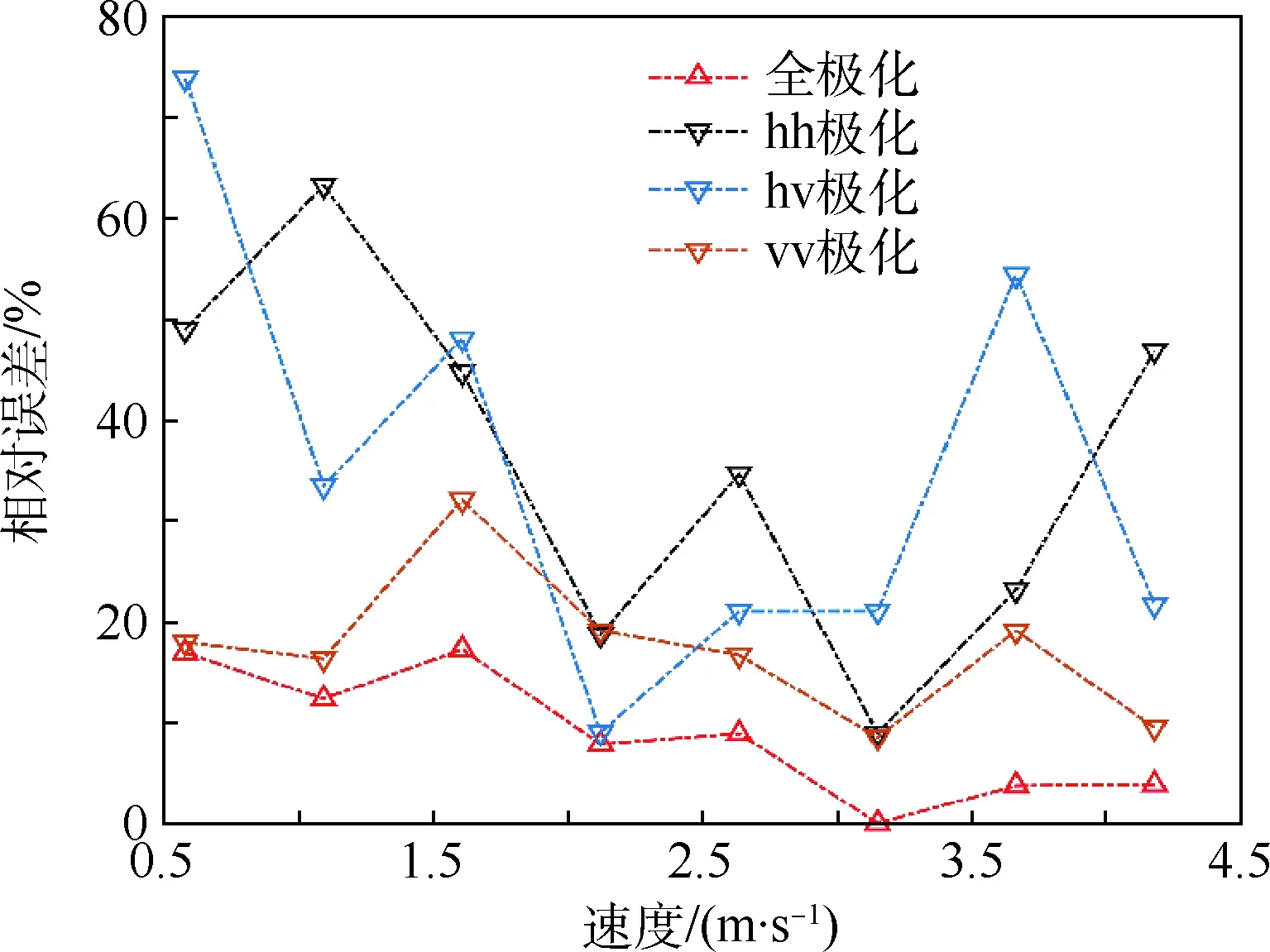
圖8 目標徑向速度估計相對誤差Fig.8 Relative estimation error of target radial velocity

圖9 估計點數對SICP性能的影響Fig.9 Performance of SICP vs. estimation point number

4 結 論

本文對如何利用AT-POLINSAR進行慢動目標CFAR檢測的問題進行了研究。在對單基線AT-POLINSAR進行回波建模的基礎上，針對其高維矢量干涉數據提出了基于次優干涉相干度準則。實驗結果表明：

1) 次優極化能使雜波背景與目標均獲取較高的相干度，但目標的相干度取值與目標特性有關。

2) 次優極化因其具有線性加權矢量,故統計分布類型與單極化相同，從而單極化AT-INSAR慢動目標檢測理論能夠通過其擴展至全極化并實現AT-POLINSAR的慢動目標CFAR檢測。

3) 將單極化檢測器應用到次優極化，檢測器的性能排序與單極化情形基本一致，但通過全極化方法能顯著提高干涉系統對慢小目標的檢測概率。

AT-POLINSAR在慢小目標CFAR檢測方面具有絕對的優勢，但需要指出的是，目前仍然沒有實際的AT-POLINSAR系統，為快速獲取AT-POLINSAR半實測等效數據進行檢測算法研究，并將極化干涉方法應用于實際POLSAR系統的GMTI，在下一步的研究中可參考文獻[25]的單通道ATI方法展開單通道POLSAR ATI的研究。