葉片表面粗糙條件下鈍尾緣翼型優化設計

張 旭 張孟潔 王格格 李 偉 阮江濤

1.天津工業大學天津市現代機電裝備技術重點實驗室，天津，300387 2.建筑安全與環境國家重點實驗室，北京，100013 3.天津城建大學能源與安全工程學院，天津，300384

0 引言

風力機多工作在高寒、沿海、風沙頻繁等環境惡劣的地區，其葉片表面經常會附著灰塵、昆蟲、雨雪等污垢。污垢增大了葉片表面的粗糙度，并導致風力機的年發電量大大降低[1-3]。對粗糙度敏感性低的翼型的設計，是減輕或消除附著污垢對翼型氣動性能影響的有效解決方案，進而可保證風力機在葉片表面粗糙條件下的高效運行。

翼型直接優化設計能很好地解決難以給定恰當目標壓力和速率分布的問題，但需要對翼型進行型線參數化表達[4]。文獻[5-9]采用Bézier函數、Hicks-Henne函數構造翼型參數化表達式，利用遺傳算法并結合XFOIL軟件以及人工神經網絡模型等進行翼型的優化設計。文獻[10]探討了各種翼型的前緣粗糙度敏感特性，并基于翼型廣義泛函集成表征形式優化出一種新翼型。研究發現，廣義泛函集成表達方法相比于其他翼型型線表征形式，更易于優化和擴展形成新的翼型型線，但不能很好控制中等和大厚度翼型尾緣處的型線[11-12],因此，文獻[12]提出翼型廣義泛函集成表達與B樣條曲線相結合的方法，以此進行風力機翼型型線的優化設計。

鈍尾緣改型設計可以有效改善表面粗糙翼型的氣動性能。BAKER等[13]實驗研究了對稱加厚的不同翼型，發現適度增加尾緣厚度可增大升阻比并降低前緣粗糙敏感度。楊瑞等[14]采用CFD方法模擬薄、鈍尾緣翼型的氣動性能，結果表明鈍尾緣翼型增大了最大升力系數，并減小了前緣污染對升力特性的影響。

鑒于優化設計和鈍尾緣改型均能提高表面粗糙翼型的氣動性能，本文結合廣義泛函集成表達和B樣條曲線來形成鈍尾緣翼型型線參數化表達式，利用粒子群算法耦合XFOIL軟件進行翼型的優化設計，平移優化后鈍尾緣翼型吸力面距前緣0.1c(c為弦長)處添加一凸臺，來研究表面粗糙翼型鈍尾緣優化前后的氣動性能和流場特性。

1 鈍尾緣翼型型線的表達

采用廣義泛函集成表達方法描述上翼面距前緣0.4c和下翼面距前緣0.5c之前的型線，則翼型的坐標分量為[12]

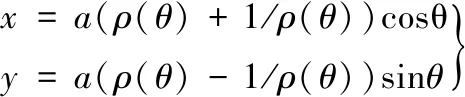
(1)

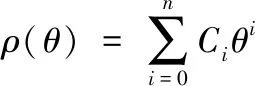
(2)

式中：a為1/4弦長；θ為幅角；ρ(θ)為翼型形狀函數；Ci為多項式系數，C0=1。

為保證翼型型線廣義泛函集成表達與B樣條曲線在結合點處的連續、光滑，采用3次B樣條曲線表示上翼面距前緣0.4c和下翼面距前緣0.5c之后的型線，則型線的坐標分別為

(3)

t∈[0, 1]

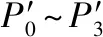
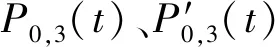
(4)

2 表面粗糙鈍尾緣翼型的優化設計

基于上述鈍尾緣翼型型線參數化表達方法，利用MATLAB編寫粒子群優化算法程序，結合XFOIL軟件計算翼型氣動性能，進行鈍尾緣翼型優化設計。平移優化后翼型指定位置坐標添加一凸臺來獲得表面粗糙的鈍尾緣翼型。

2.1 設計變量和約束條件

為較好控制鈍尾緣翼型的型線，選取形狀函數控制方程的前11項系數C1～C11、B樣條曲線控制參數以及尾緣厚度和其分配比為優化設計變量X：

(5)

在鈍尾緣翼型優化過程中，需限定控制變量的范圍，以避免形成的型線不具有翼型的形狀特征，則優化變量邊界約束條件為

xmin≤x≤xmax

(6)

式中，x為設計變量X中的任一分量；xmin、xmax分別為x的下限和上限。

大部分風力機葉片在其主要功率產生區采用最大厚度為0.12～0.25的翼型，又由于翼型的相對厚度對葉片結構特性的影響不容忽視，故翼型厚度tr的約束條件為

可以看出，存在“學校管理層不重視數據利用;未形成制度，決算數據利用率不高;認為未形成橫向對比數據庫，數據很難進行定性、定量分析”等三個方面的差距，表明區外高校在對決算報表利用方面做了很多改良，信息化已把財務人員從手工計算分析數據轉為運用EViews等專業統計軟件來分析趨向。

0.12≤tr≤0.25

(7)

2.2 目標函數

升阻力系數、阻力系數是研究風力機翼型氣動性能的兩個重要指標。為使翼型在風力機正常運行工況下具有良好的氣動性能，選擇翼型的最大升阻比為目標函數：

f(X)=max(CL/CD)

(8)

式中，CL、CD分別為翼型的升力系數和阻力系數。

2.3 粗糙翼型型線優化設計

粒子群算法具有實現容易、精度高、收斂快等優點，解決實際問題的效率很高。XFOIL軟件基于源面方法和邊界層理論計算翼型的氣動性能，計算的過程較簡單且精度較高[15]。因此，基于建立的鈍尾緣翼型型線優化模型，采用粒子群算法耦合XFOIL軟件，并通過MATLAB編寫優化程序，對S812翼型進行型線優化設計。S812翼型用于風力機葉片的主要功率產生區，最大相對厚度為21%并位于0.39c處，且最大相對彎度為1.57%。

取雷諾數Re=1×106，馬赫數Ma=0.04，種群規模為20，最大進化代數為300，學習因子S1、S2為0.5，變量維數為21。為使算法程序既有較強的搜索能力，又有較好的收斂性，慣性權重w=wmax-m(wmax-wmin)/mmax[16]，其中，wmax、wmin分別為慣性權重的最大值和最小值，依據經驗取1.2和0.4；m和mmax分別為當前的進化代數和最大的進化代數。

本文平移優化后翼型指定位置的坐標，在翼型吸力面距前緣0.1c處添加一高0.015c、寬0.04c的凸臺，以模擬翼型表面粗糙情況，從而得到表面粗糙S812翼型(取名為S812-R翼型，R表示粗糙)及其鈍尾緣改型S812-R-BT(BT表示鈍尾緣)的形狀，如圖1所示。S812-R-BT翼型的尾緣厚度為0.039 8c，上下翼面尾緣厚度比為1∶13.16。

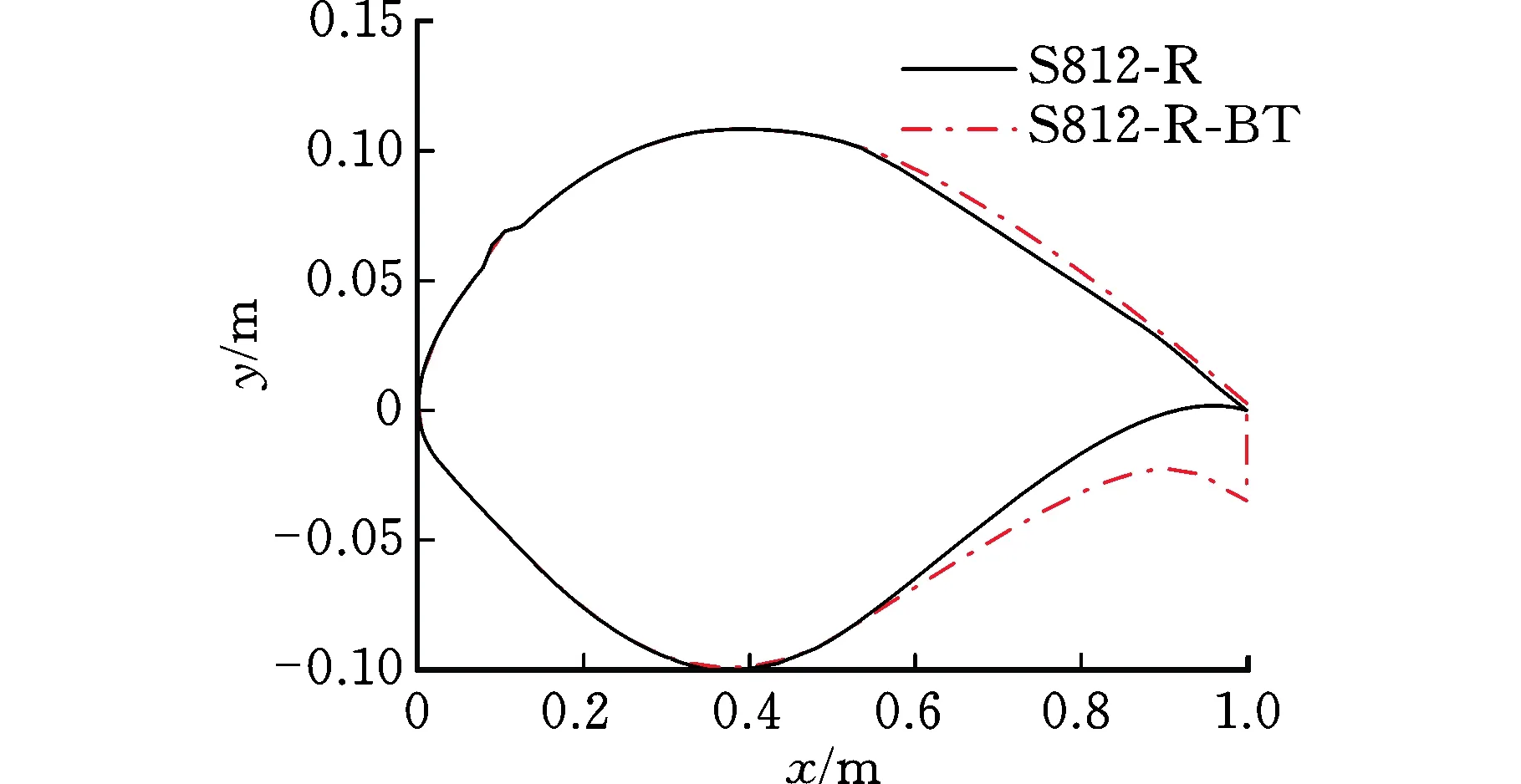
圖1 優化前后表面粗糙翼型型線Fig.1 Profiles of rough airfoil before and after optimization

3 優化前后的氣動性能和流場特性

利用基于CFD方法的FLUENT軟件，計算S812翼型的升力系數、阻力系數，并比較數值計算結果與實驗數據，研究表面粗糙翼型鈍尾緣優化前后的升力系數、阻力系數、升阻比、壓力系數和流場特性，分析鈍尾緣優化設計對粗糙翼型氣動性能的提升效果。

3.1 數值計算方法

直徑50c的半圓形和長50c、寬25c的矩形構成計算域，翼型位于半圓中心。計算域左側以及上下兩側采用速度進流邊界條件，速度由Re=1×106確定；計算域右側采用壓力出流邊界條件，表壓力給定0；翼型表面滿足固壁絕熱無滑移條件。利用C型結構化網格劃分，并對翼型前后緣以及翼型附近的網格進行局部加密。控制方程組采用連續性方程和二維不可壓縮Navier-Stokes方程，湍流模型選用較適合模擬穩態繞流情況的k-ωSST模型[17]。各方程離散采用二階迎風格式，壓力和速度耦合采用SIMPLE算法。速度和連續性方程的殘差值分別為10-6和10-4，j和ω的殘差值均為10-5。

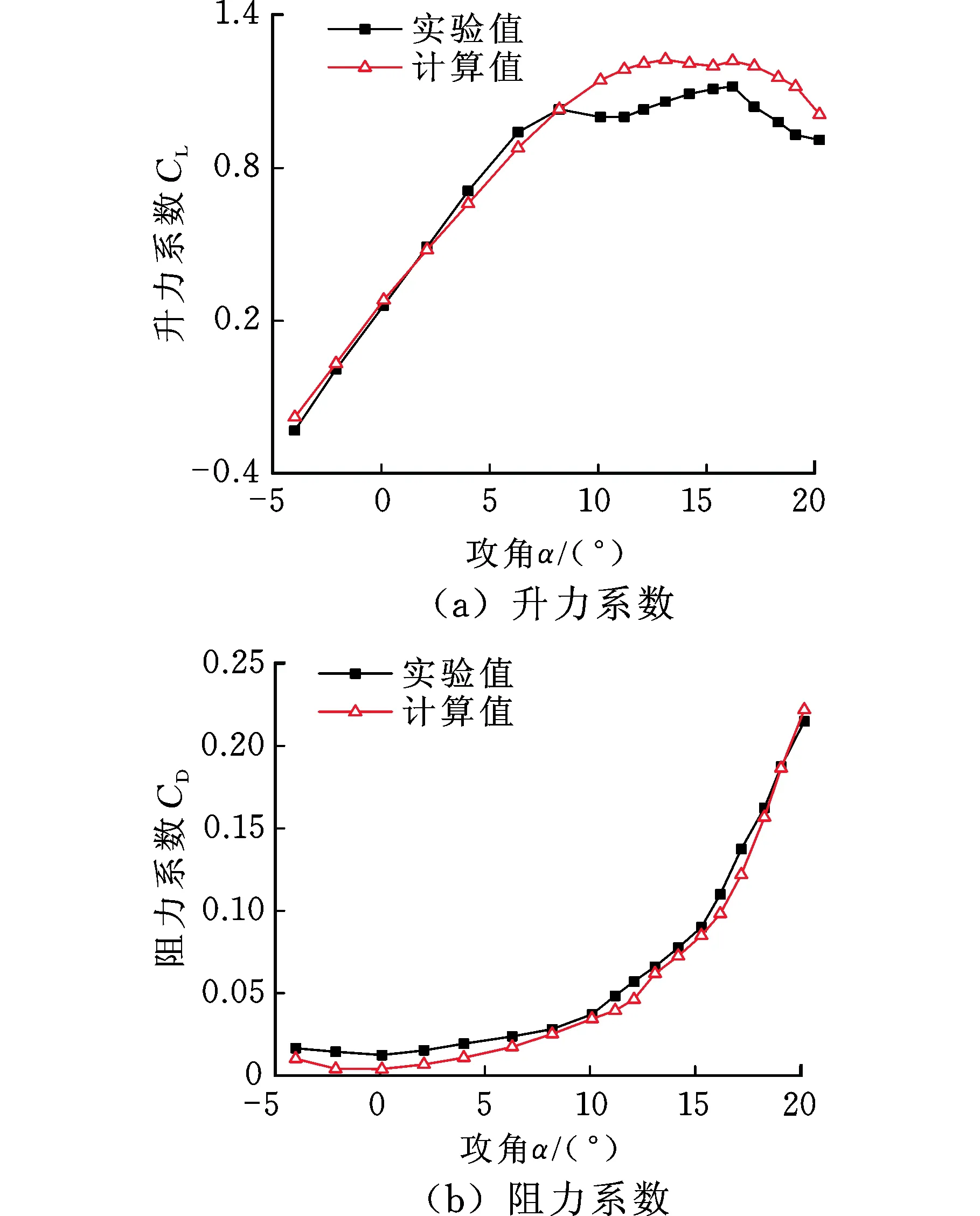
圖2 S812翼型計算與實驗的結果Fig.2 Calculated and experimental data for S812 airfoil

3.2 表面粗糙翼型鈍尾緣優化前后的氣動性能

鈍尾緣優化前后，表面粗糙翼型的升力系數、阻力系數和升阻比隨攻角變化的曲線見圖3。由圖3a、圖3b可以看出，S812-R-BT翼型的升力系數相較于S812R翼型明顯增大；S812-R-BT翼型的阻力系數在17.2°攻角之前與S812-R翼型的阻力系數非常接近，17.2°攻角之后大于S812-R翼型的阻力系數。由圖3c可以看出，S812-R-BT翼型的升阻比在攻角小于17.2°時明顯大于S812R翼型的阻力比，17.2°攻角之后與S812-R翼型十分接近；S812-R-BT翼型的最大升阻比較S812-R翼型的最大升阻比有大幅提高。

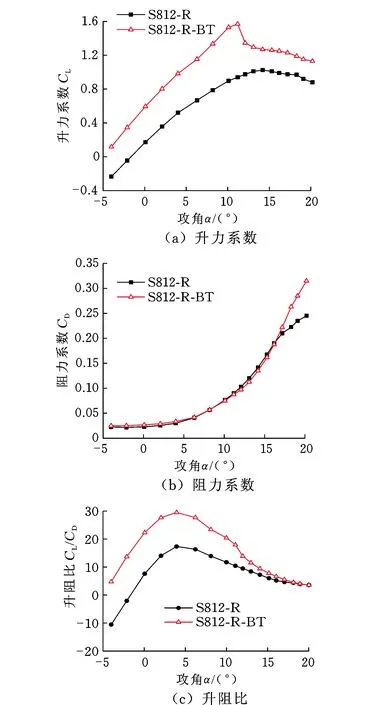
圖3 S812-R和S812-R-BT翼型的升力系數、阻力系數和升阻比Fig.3 Lift, drag coefficients and lift-drag ratios of S812-R and S812-R-BT airfoils

3.3 表面粗糙翼型鈍尾緣優化前后的壓力系數

S812-R翼型及其優化后鈍尾緣翼型S812-R-BT的表面壓力分布如圖4所示。由圖4可以看出，17.2°攻角之前，S812-R-BT翼型吸力面的壓力系數減小，壓力面的壓力系數增大；18.3°攻角時，吸力面的壓力系數稍微增大，壓力面的壓力系數也是如此。所以，表面粗糙翼型鈍尾緣優化后，上下翼面的壓差增加，即S812-R-BT翼型的升力系數高于S812-R翼型，這與圖3的規律一致。

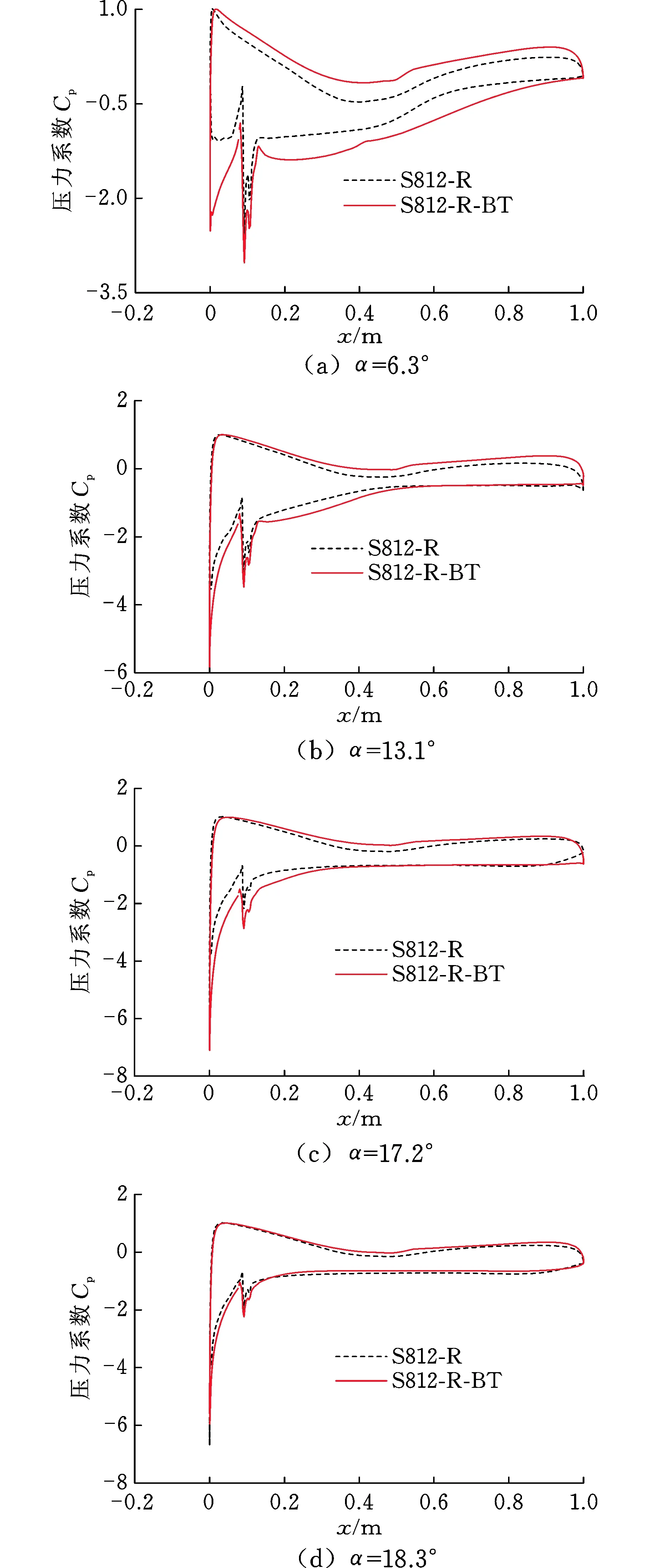
圖4 S812-R和S812-R-BT翼型的表面壓力分布Fig.4 Pressure distributions around S812-R and S812-R-BT airfoils

3.4 表面粗糙翼型鈍尾緣優化前后的流場特性

由圖5可以看出，2.1°攻角時，S812-R翼型上翼面前緣凸臺后面形成較小的漩渦，尖尾緣處未發生流動分離；S812-R-BT翼型凸臺后面沒有漩渦，鈍尾緣處卻存在一對方向相反交替脫落的漩渦，這是因為鈍尾緣對氣流形成阻擋作用。同時，鈍尾緣處的漩渦使吸力面的氣流發生下洗作用，因而S812-R-BT翼型壓力面的壓力增大，吸力面的壓力減小，進而引起升力系數增大。

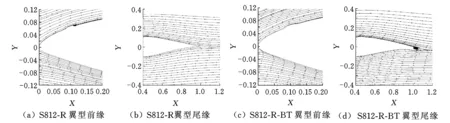
圖5 S812-R和S812-R-BT翼型的流線圖(α=2.1°)Fig.5 Streamlines around S812-R and S812-R-BT airfoils(α=2.1°)

由圖6可以看出，6.3°攻角時，S812-R翼型凸臺后面仍存在小的漩渦， 吸力面尾緣處的漩渦交替脫落，且已經發生流動分離，這對應于圖3中升力系數曲線斜率稍有下降的現象；而S812-R-BT翼型依然僅在鈍尾緣后面存在一對交替脫落的漩渦，且其尺寸大于2.1°攻角時的漩渦。

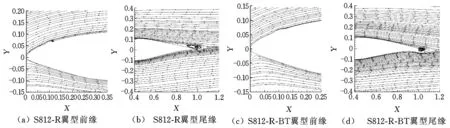
圖6 S812-R和S812-R-BT翼型的流線圖(α=6.3°)Fig.6 Streamlines around S812-R and S812-R-BT airfoils(α=6.3°)

由圖7～圖9可以看出，當攻角增大到17.2°時，S812-R-BT翼型凸臺后面才產生漩渦。

由圖5～圖9還可以看出，隨著攻角的增加，S812-R翼型及其鈍尾緣改型S812-R-BT的凸臺后面漩渦逐漸增長，尾緣處的漩渦也持續增長并向吸力面前緣擴張，且S812-R翼型尾緣處的漩渦更靠近前緣；S812-R-BT翼型鈍尾緣后面的漩渦使吸力面氣流的下洗作用持續發生，因而S812-R-BT翼型的升力系數一直大于S812-R翼型的升力系數。

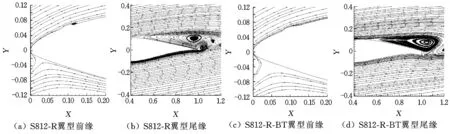
圖7 S812-R和S812-R-BT翼型的流線圖(α=13.1°)Fig.7 Streamlines around S812-R and S812-R-BT airfoils(α=13.1°)

圖8 S812-R和S812-R-BT翼型的流線圖(α=17.2°)Fig.8 Streamlines around S812-R and S812-R-BT airfoils(α=17.2°)

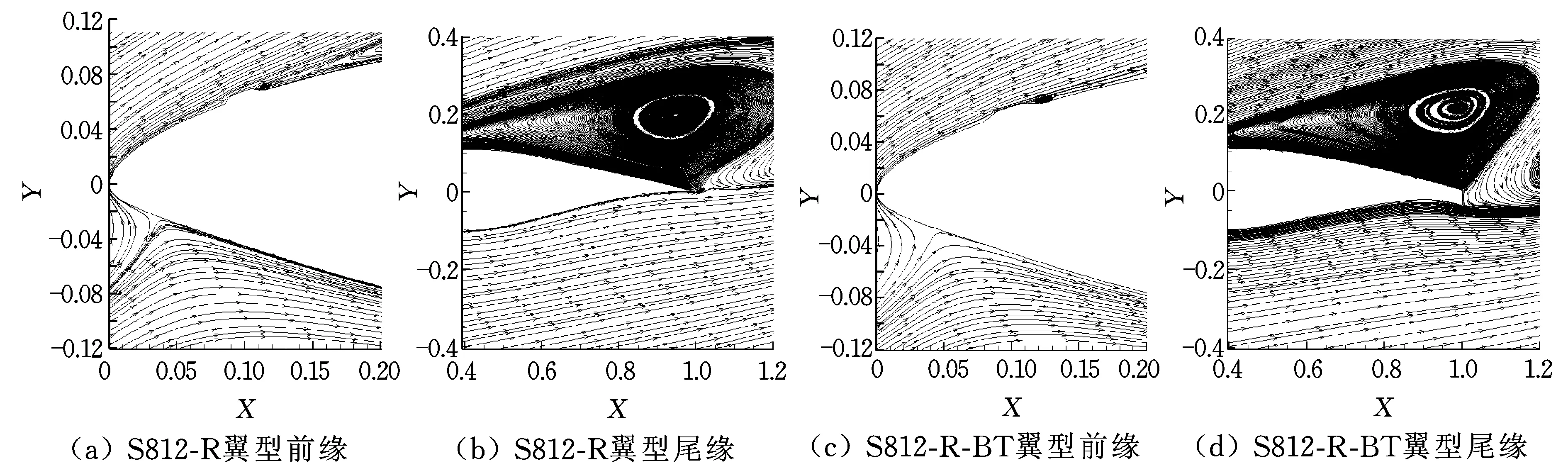
圖9 S812-R和S812-R-BT翼型的流線圖(α=18.3°)Fig.9 Streamlines around S812-R and S812-R-BT airfoils (α=18.3°)

4 結論

(1)以翼型型線控制方程組的形狀函數系數、B樣條曲線控制點以及尾緣厚度及其在上翼面分配比為設計變量，利用粒子群算法并結合XFOIL軟件進行了S812翼型鈍尾緣優化；平移優化后，在翼型吸力面0.1c處坐標添加了一高0.015c、寬0.04c的凸臺，得到尾緣厚度為0.039 8c且上下翼面尾緣厚度比為1∶13.16的表面粗糙S812翼型鈍尾緣改型。

(2)表面粗糙翼型鈍尾緣優化后，升力系數大幅增大；阻力系數在17.2°攻角之前與原型相差不多，在17.2°攻角后阻力系數明顯增大；升阻比在17.2°攻角之前顯著增大，17.2°攻角后與原型基本一致，最大升阻比明顯增大。

(3)鈍尾緣翼型尾緣處的漩渦對吸力面的氣流造成下洗作用，使得吸力面和壓力面的壓差變大，推遲了翼型的失速,因而，表面粗糙翼型鈍尾緣優化后，氣動性能得到明顯提高。