鎂合金非對稱應力載荷下的低周疲勞損傷演化和壽命預測

陳 凌 張賢明 劉 飛 歐陽平 賈艷艷

1.重慶工商大學廢油資源化技術與裝備工程研究中心，重慶，400067 2.重慶大學機械工程博士后科研流動工作站，重慶，400044 3.重慶工商大學制造裝備機構設計與控制重慶市重點實驗室，重慶，400067

0 引言

近年來，隨著鎂合金在汽車、航空航天等領域的大量應用，鎂合金的疲勞研究得到了廣泛的關注。目前，主要的研究集中在材料的低、高周疲勞行為[1-3]及稀土元素、熱處理等工藝對材料的性能強化[4-6]等方面，對鎂合金非對稱載荷加載的疲勞研究較少。實際工況中，鎂合金部件多承受非對稱循環應力載荷的作用，除疲勞載荷外，部件還承受平均應力導致的棘輪效應的影響。針對鎂合金非對稱應力載荷下的疲勞，LIN等[7-10]的研究主要集中在材料非對稱循環應力載荷下的棘輪效應及其影響因素，缺乏相應工況下的疲勞損傷演化和壽命預測的研究。

材料的低周疲勞損傷演化和壽命預測是相應零部件強度設計、優化和安全評估的基礎，目前關于鎂合金的低周疲勞損傷演化和壽命預測的研究較少，主要以經典的Miner線性累積損傷理論、Manson-Coffin公式、Basquin公式及其在此基礎上的修正[11-14]為主，缺乏對鎂合金非對稱載荷加載的低周疲勞損傷演化和壽命預測的研究。

筆者在室溫環境下，通過鑄造鎂合金AZ91D和變形鎂合金AZ31B非對稱應力載荷的低周疲勞試驗，基于連續損傷力學，分別選取彈性模量、等效模量、總應變能密度以及平均應變的變化作為損傷變量，對鎂合金非對稱應力載荷下的低周疲勞損傷演化進行分析，建立了相應的低周疲勞壽命預測模型。為驗證各損傷變量對應的壽命模型預測效果，選取各壽命段采樣數據，用上述模型進行了鎂合金非對稱應力載荷下的低周疲勞壽命預測。

1 低周疲勞損傷演化和壽命預測

1.1 損傷變量與低周疲勞損傷演化

損傷變量是一種用于描述材料內部損傷狀態變化及其對材料力學作用影響的內部狀態變量。合適的損傷變量可以反映材料的低周疲勞損傷演化過程。對于應力控制的低周疲勞來說，通常將彈性模量E的變化作為損傷變量：

DE=1-EN/E0

(1)

式中，DE為以彈性模量的變化為損傷變量定義的材料損傷；EN為材料循環過程中的彈性模量；E0為材料初始無損傷時的彈性模量。

在式(1)的基礎上，用等效模量Eeq代替彈性模量，可得損傷變量：

DE,eq=1-Eeq,N/Eeq,0

(2)

Eeq=(σmax-σmin)/(εmax-εmin)

(3)

式中，DE,eq為以等效模量的變化為損傷變量定義的材料損傷；Eeq,N為材料循環過程中的等效模量；Eeq,0為材料初始無損傷時的等效模量；σmax、σmin分別為每一循環過程中的最大應力和最小應力；εmax、εmin分別為每一循環過程中的最大應變和最小應變。

選擇彈性模量或等效模量的變化作為損傷變量，對循環軟化的材料較為適用。對于循環硬化的材料，在循環初始快速硬化階段，選擇彈性模量或等效模量的變化反映疲勞損傷的效果較差。對于非對稱應力加載下的疲勞損傷，彈性模量或等效模量不能很好地反映平均應力導致的棘輪效應的影響。

為反映非對稱應力加載過程中棘輪效應以及累積塑性變形對疲勞損傷的影響，選擇總應變能密度ΔWt或平均應變εm的變化作為損傷變量：

DΔWt=1-ΔWt,0/ΔWt,N

(4)

Dεm=εm,N/εm,f

(5)

式中，DΔWt為以總應變能密度的變化為損傷變量定義的材料損傷；Dεm為以平均應變的變化為損傷變量定義的材料損傷；ΔWt，0為材料初始無損傷時的總應變能密度；ΔWt,N為材料循環過程中的總應變能密度；εm,N為材料循環過程中的平均應變；εm,f為材料斷裂時的平均應變。

對于式(4)所定義的損傷變量，總應變能密度為彈性應變能密度和塑性應變能密度之和[15]：

ΔWt=ΔWe+ΔWp

(6)

(7)

其中，ΔWe為彈性應變能密度，用來反映非對稱載荷下平均應力的影響；|Δσ|為名義應力最大值與最小值的差值；σm為平均應力；ΔWp為塑性應變能密度，用來反映累積塑性變形的影響，由循環過程中遲滯徊線所圍面積得到。

材料初始無損傷時的塑性累積為零，因此，對于式(4)所定義的損傷變量，材料初始無損傷時的總應變能密度取彈性應變能密度。

式(5)定義的損傷變量以平均應變的變化來綜合反映棘輪效應和塑性變形的累積，物理意義明確，同時測量較為容易。

通過上述各式定義的損傷變量，可計算得到各循環周次鎂合金材料的材料損傷，通過材料損傷隨循環周次的變化即可分析鎂合金材料的低周疲勞損傷演化規律。

1.2 低周疲勞損傷及壽命預測模型

(8)

式中，D為材料損傷變量。

對損傷動力學方程(式(8))進行積分，積分上下限DN=0=D0，DN=Nf=1 ，可得材料的低周疲勞損傷模型：

D=1-(1-D0)(1-N/Nf)k

(9)

式中，D0為材料常數，代表材料初始循環時的損傷值。

在實際的疲勞試驗中，疲勞試驗機采用漸進保護式加載，即加載幅度以Δσ/4、Δσ/2、3Δσ/4、Δσ的應力歷程進行，因此，實際疲勞工況中材料初始循環的損傷除材料本身的初始損傷外，還包括前期加載幅度小于|Δσ|時造成的材料損傷。

在式(9)基礎上，聯立式(1)、式(2)、式(4)、式(5)，可得不同損傷變量下的低周疲勞預測壽命模型：

(10)

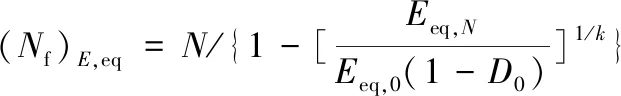
(11)

(12)

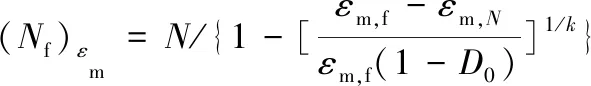
(13)

式中，(Nf)E、(Nf)E,eq、(Nf)ΔWt、(Nf)εm分別代表以彈性模量、等效模量、總應變能密度和平均應變的變化作損傷變量所得壽命預測模型的疲勞壽命。

基于式(10)～式(13)，根據循環周次和對應的彈性模量、等效模量、總應變能密度以及平均應變等疲勞參數，即可得到相應的疲勞壽命，進而考察不同損傷變量下基于材料低周疲勞損傷模型的壽命模型預測效果，為相應工況下鎂合金材料的損傷評估和壽命預測提供理論依據。

2 試驗結果及討論

試驗在電液伺服疲勞試驗機上進行，試驗溫度為25 ℃，試驗材料為鑄造鎂合金AZ91D和變形鎂合金AZ31B，試驗材料室溫下的力學性能和化學成分見文獻[15]。試驗用疲勞試樣為光滑圓棒試樣，參照GB/T 15248-2008[18]進行制作。試驗控制模式為應力控制，控制波形為三角波，采用脈動循環(應力比為0)，加載頻率為3～5 Hz。具體的試驗數據和試驗結果見表1、表2，試驗裝置和試樣尺寸見圖1，其中，σa為名義應力幅，Δσ為各義應力范圍。

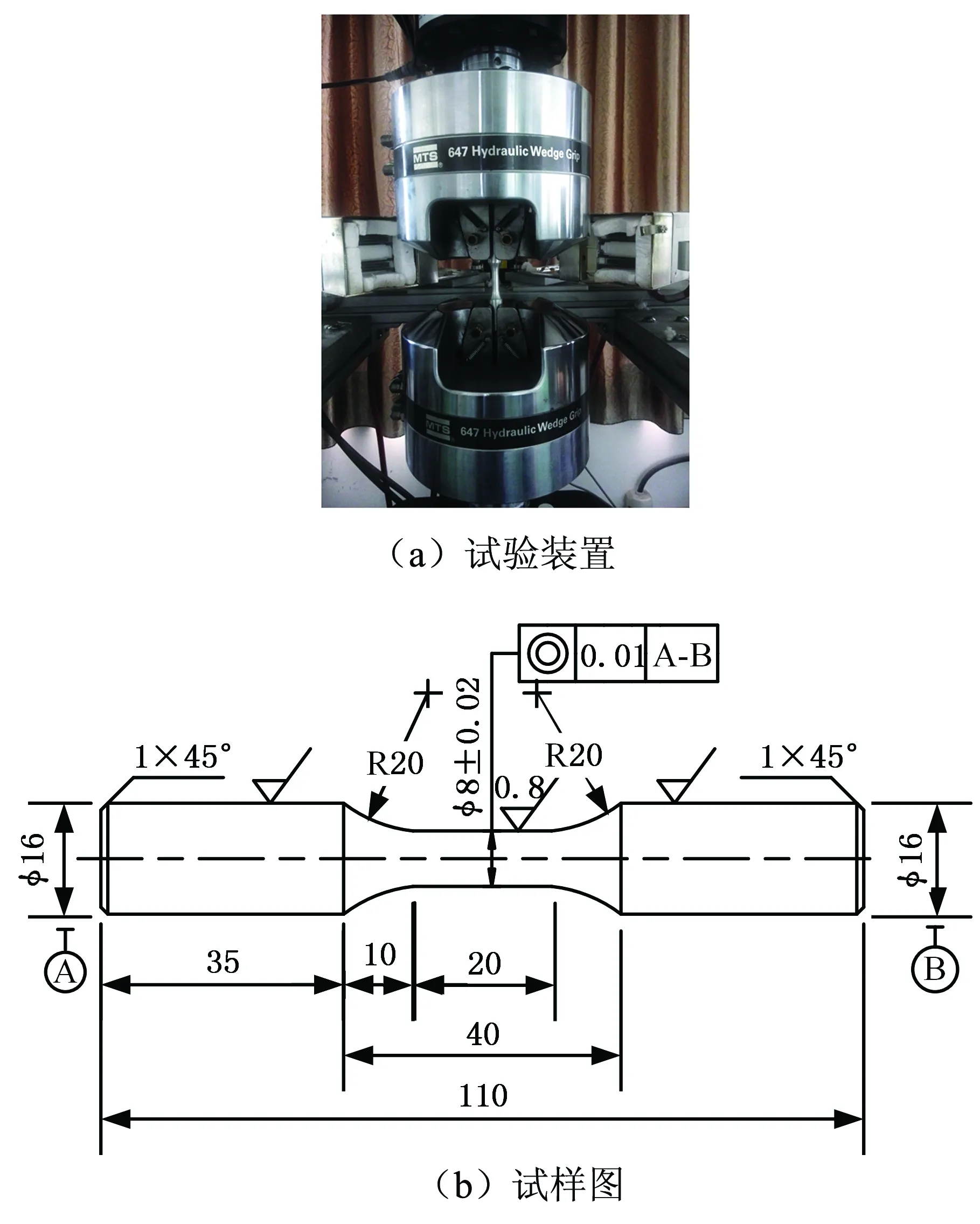
圖1 疲勞試驗裝置及試樣Fig.1 Equipment and specimen in fatigue experiments

表1 鑄造鎂合金AZ91D低周疲勞試驗數據及結果(25 ℃)

表2 變形鎂合金AZ31B低周疲勞試驗數據及結果(25 ℃)

圖2、圖3分別為鑄造鎂合金AZ91D和變形鎂合金AZ31B的彈性模量、等效模量隨壽命分數N/Nf的變化曲線，其中，彈性模量通過材料每循環應力-應變曲線(遲滯徊線)的彈性段獲得，等效模量的計算公式為式(3)。由圖2、圖3可知：①鑄造鎂合金AZ91D的彈性模量、等效模量隨循環周次的增加而增大，材料的彈性模量、等效模量在循環后期才出現下降趨勢，表明鑄造鎂合金AZ91D在循環過程中出現循環硬化；當循環周次接近疲勞壽命時，材料才出現軟化趨勢。②變形鎂合金AZ31B的彈性模量、等效模量在初始循環階段隨循環周次的增加而降低，之后隨循環周次的增加而增大；材料的彈性模量、等效模量在循環后期才出現下降趨勢，表明變形鎂合金AZ31B經初始階段的循環軟化后，在循環過程中呈現循環硬化，當循環周次接近疲勞壽命時，材料才出現軟化趨勢。

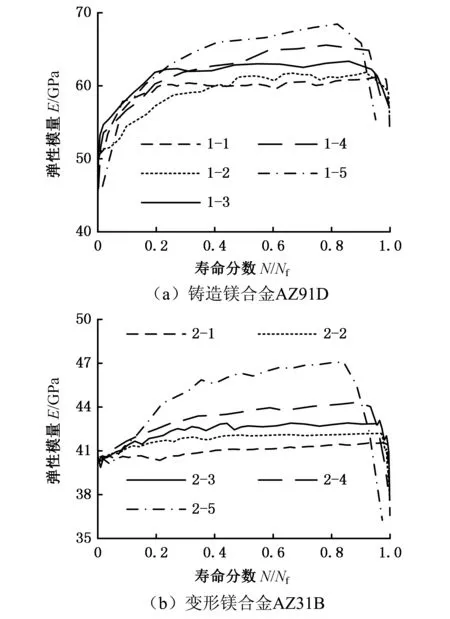
圖2 鎂合金彈性模量隨壽命分數變化Fig.2 Change of elastic modulus of magnesium alloys with life fraction

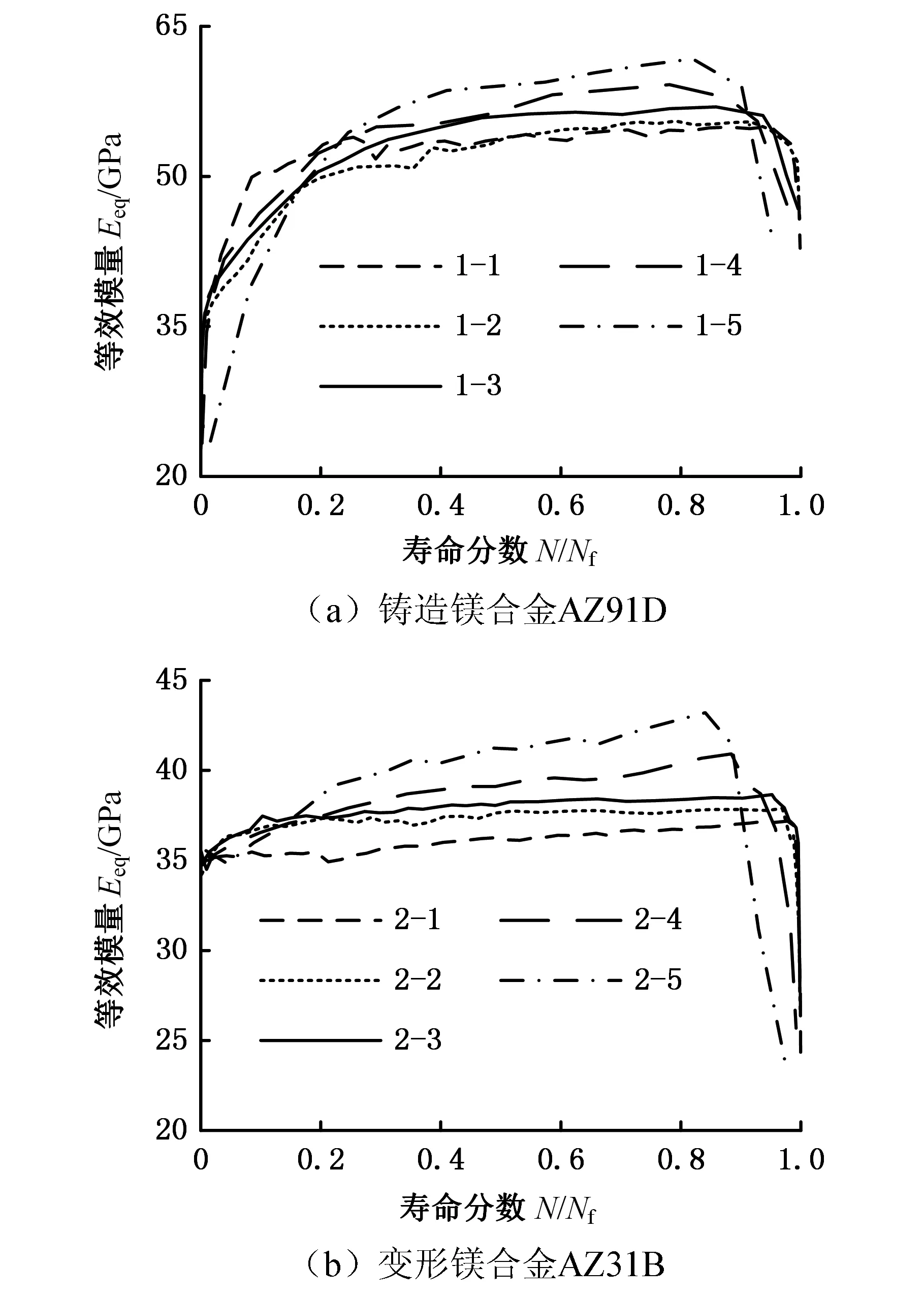
圖3 鎂合金等效模量隨壽命分數變化Fig.3 Change of equivalent modulus of magnesium alloys with life fraction

由式(1)、式(2)可知，將彈性模量或等效模量的變化作為損傷變量，對循環硬化階段的材料損傷進行描述時會出現損傷為負的情況，不能反映材料的損傷情況。AZ91D、AZ31B在大部分循環階段內均呈現循環硬化，因此，利用彈性模量或等效模量的變化作為損傷變量不適用于材料AZ91D、AZ31B非對稱應力載荷下的低周疲勞損傷描述，相對應的壽命預測模型也不適用于材料非對稱應力載荷下的低周疲勞壽命預測。

圖4、圖5分別為鑄造鎂合金AZ91D和變形鎂合金AZ31B的總應變能密度、平均應變隨壽命分數N/Nf的變化曲線，其中，總應變能密度的計算公式為式(6)。由圖4、圖5可知：鑄造鎂合金AZ91D和變形鎂合金AZ31B的總應變能密度、平均應變隨循環周次的增加而增大，當循環周次接近疲勞壽命時，總應變能密度和平均應變的增大趨勢明顯提高。總應變能密度和平均應變的變化趨勢與材料的損傷演化過程較為一致，即材料損傷隨著循環周次的增加逐漸累積，當損傷的累積到達一定程度后導致材料快速失效。

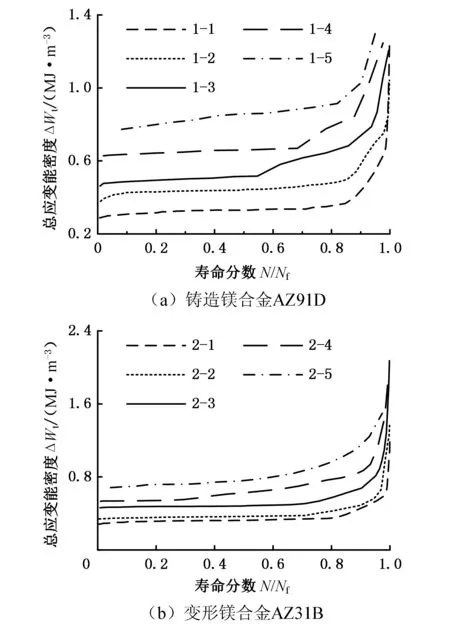
圖4 鎂合金總應變能密度隨壽命分數變化圖Fig.4 Change of total strain energy density of magnesium alloys with life fraction

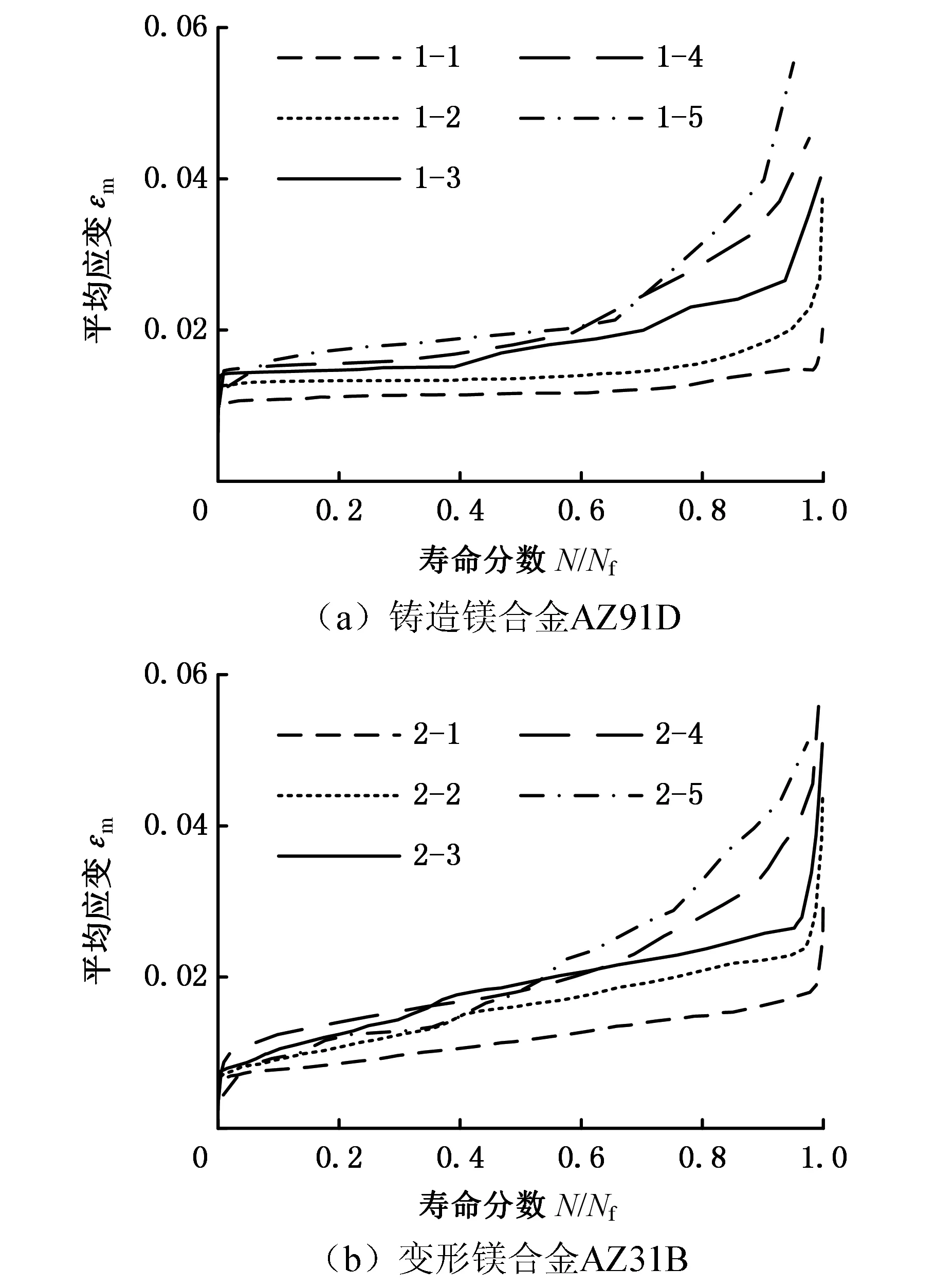
圖5 鎂合金平均應變隨壽命分數變化圖Fig.5 Change of mean strain of magnesium alloys with life fraction

根據式(4)、式(5)定義的損傷變量公式，分別計算不同壽命分數下以總應變能密度及平均應變的變化作為損傷變量時的材料損傷，可得鑄造鎂合金AZ91D和變形鎂合金AZ31B非對稱應力載荷下的低周疲勞損傷變化曲線，如圖6、圖7所示。由圖6、圖7可知，以總應變能密度及平均應變的變化作為損傷變量時，材料AZ91D、AZ31B的疲勞損傷隨壽命分數的變化具有典型的連續材料疲勞損傷演化特征，即材料的疲勞損傷隨循環周次的增加而增加，在循環的穩定階段，疲勞損傷的增加速率較小且變化不大，當循環周次接近疲勞壽命時，材料的損傷累積接近材料失效的臨界值，材料的疲勞損傷迅速增加，并快速導致材料失效。因此，用總應變能密度或平均應變的變化作為損傷變量來描述鎂合金非對稱應力載荷下的低周疲勞損傷演化是可行的。

以式(4)、式(5)定義的總應變能密度及平均應變的變化作為損傷變量，對式(9)所示的損傷模型進行擬合，可得鑄造鎂合金AZ91D和變形鎂合金AZ31B各工況下的低周疲勞損傷模型，圖8為代表性擬合圖，擬合結果見表1、表2。

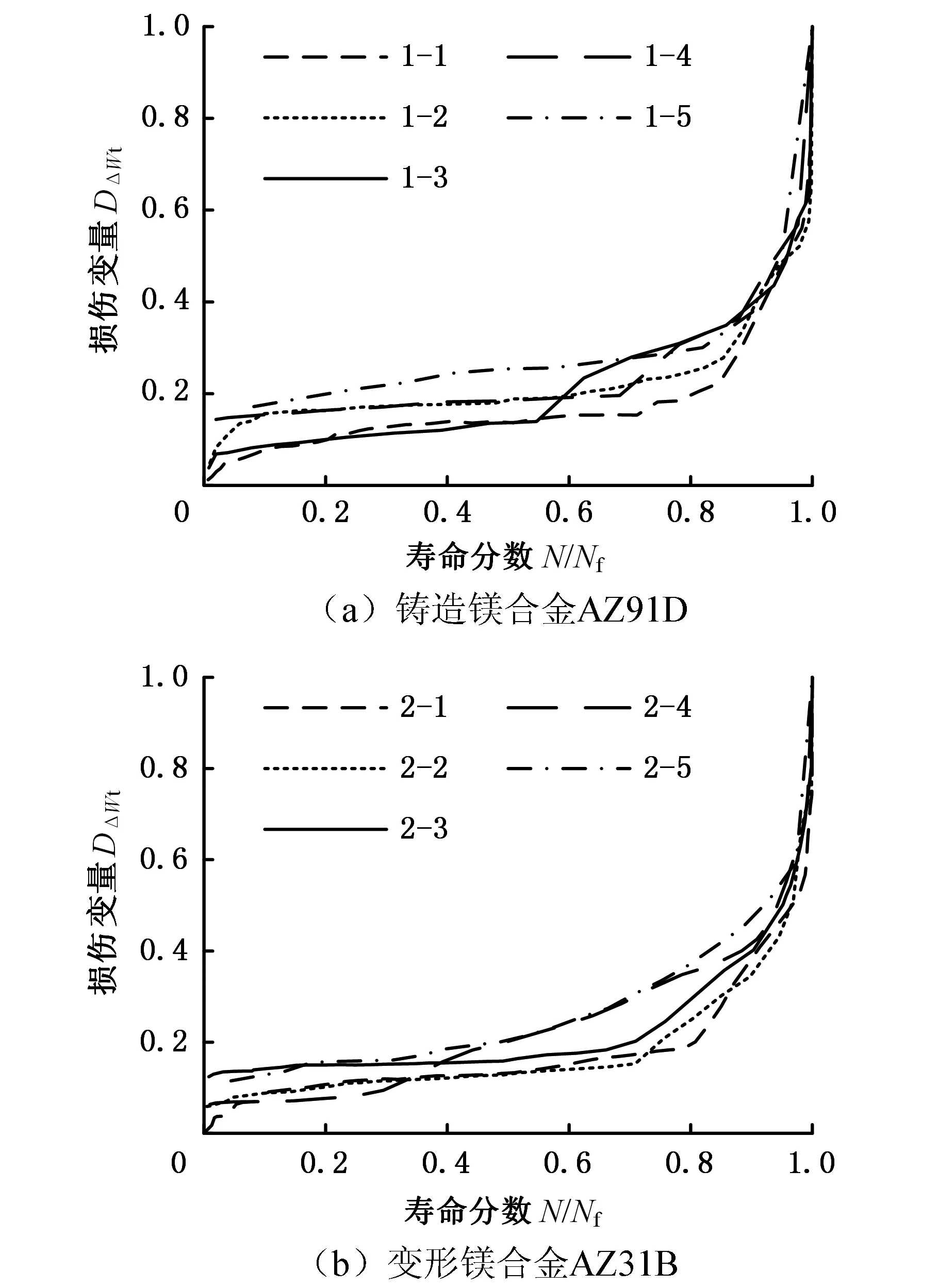
圖6 以DΔWt=1-ΔWt，0/ΔWt，N為損傷變量的鎂合金低周疲勞損傷變化曲線Fig.6 Low cycle fatigue damage change curves of magnesium alloys by defining damage variable as DΔWt=1-ΔWt，0/ΔWt，N

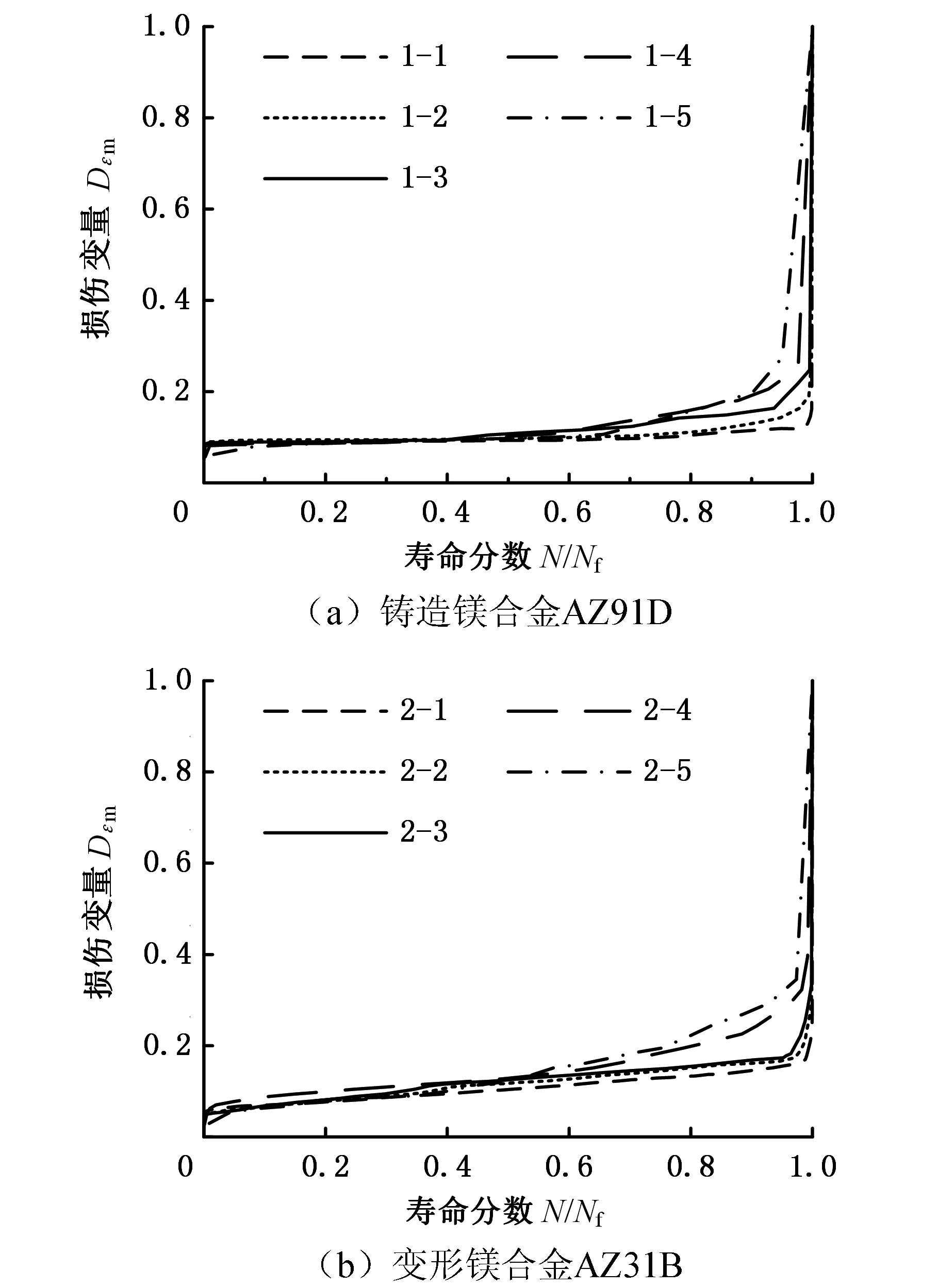
圖7 以Dεm=εm，N/εm，f為損傷變量的鎂合金低周疲勞損傷變化曲線Fig.7 Low cycle fatigue damage change curves of magnesium alloys by defining damage variable as Dεm=εm，N/εm，f

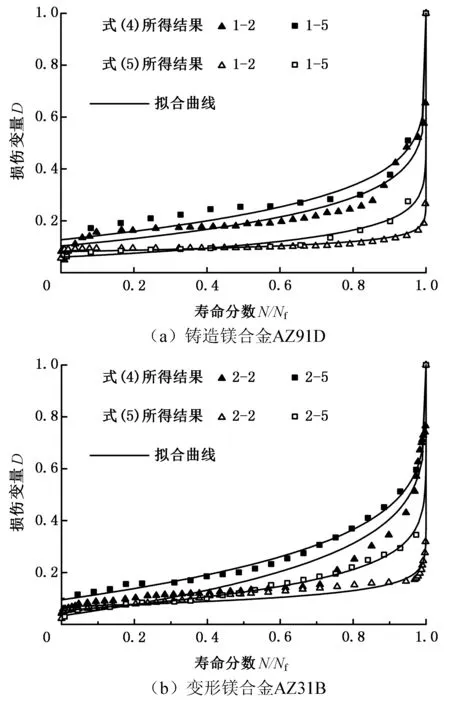
圖8 鎂合金低周疲勞損傷模型擬合圖Fig.8 Fitting curves of low cycle fatigue damage models for magnesium alloys

由圖8可以看出：選取總應變能密度或平均應變的變化作為損傷變量，基于式(9)所示損傷模型所得的損傷曲線與損傷點較符合。由于變形鎂合金的組織結構相對于鑄造鎂合金更為致密、均勻，對連續損傷力學理論的符合程度更好，因此，變形鎂合金AZ31B的損傷模型擬合曲線與損傷點的符合程度較鑄造鎂合金AZ91D好。另外，相較于總應變能密度，選取平均應變的變化作為損傷變量擬合所得損傷曲線與實測損傷點的符合程度更好。

將表1、表2所得損傷模型的材料常數k和初始損傷D0代入式(12)、式(13)，即可得到以總應變能密度及平均應變的變化為損傷變量的低周疲勞壽命預測模型。分別選取表1、表2中試驗試樣中1/4壽命分數 (Nf/4)、1/2壽命分數(Nf/2)和3/4壽命分數(3Nf/4)附近的采樣點的循環周次及相應的總應變能密度和平均應變，利用式(12)、式(13)所示模型進行材料疲勞壽命的預測，預測效果如圖9所示。由圖9可知：①以總應變能密度或平均應變的變化作為損傷變量時，低周疲勞壽命預測模型均具有較好的預測效果，所有的壽命預測結果在2倍誤差帶以內，絕大部分的壽命預測結果在1.5倍誤差帶以內；②相較于總應變能密度，以平均應變的變化作為損傷變量的預測效果更好，更多的壽命預測結果處于1.5倍誤差帶以內。

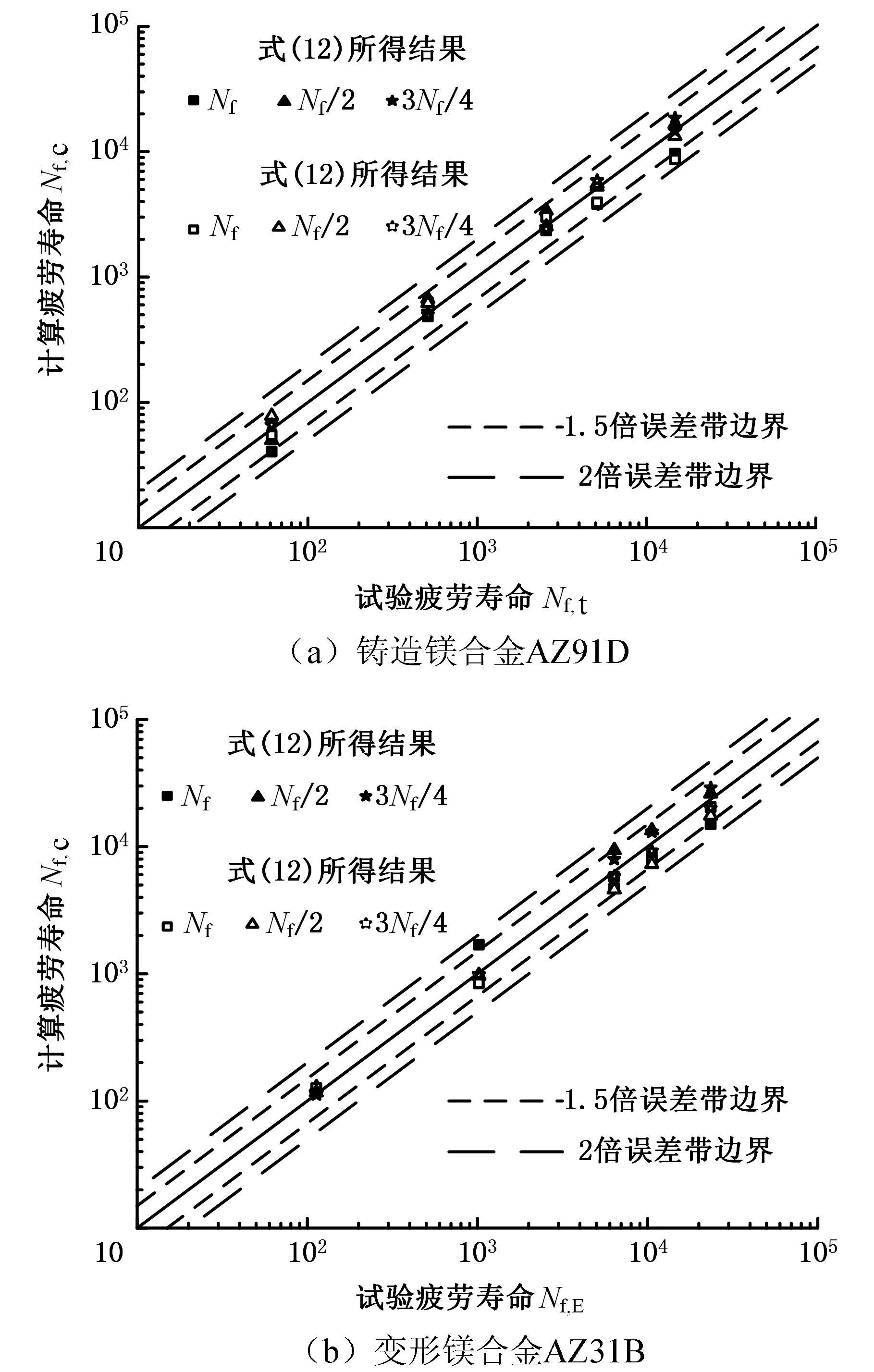
圖9 鎂合金低周疲勞壽命預測效果圖Fig.9 Low cycle fatigue prediction effects of magnesium alloys

由表1、表2可知：選取總應變能密度的變化作為損傷變量擬合所得的損傷模型材料常數k隨載荷水平的變化規律較亂，選取平均應變的變化作為損傷變量擬合所得損傷模型的材料常數k隨載荷水平的增加而增大。對于非對稱載荷應力載荷下的低周疲勞來說，棘輪效應和塑性變形累積之間存在相互耦合，單純采用總應變能密度不能很好地反映兩者之間的耦合，導致損傷模型的材料常數k隨載荷水平的變化規律較亂。棘輪效應、塑性變形累積及其相互耦合均會造成平均應變的增大，采用平均應變的變化作為損傷變量可以綜合反映棘輪效應和塑性變形累積的影響，故損傷模型的材料常數k與載荷水平的對應關系較好。因此，相較于總應變能密度，選取平均應變的變化作為損傷變量所得的損傷曲線具有更好的代表性，可以較好地反映載荷對疲勞損傷的影響。

3 結論

(1)以總應變能密度或平均應變的變化作為損傷變量，能夠反映非對稱應力加載過程中棘輪效應以及累積塑性變形對疲勞損傷的影響，可用來描述鎂合金非對稱應力載荷下的低周疲勞損傷演化。受限于材料的循環特性，將彈性模量或等效模量的變化作為損傷變量，不合適描述鎂合金非對稱應力載荷下的低周疲勞損傷。

(2)基于連續損傷力學，用總應變能密度及平均應變的變化作為損傷變量表示損傷，建立了鎂合金非對稱應力載荷下的低周疲勞壽命預測模型。使用該模型進行了鑄造鎂合金AZ91D和變形鎂合金AZ31B室溫環境非對稱應力載荷下的低周疲勞壽命預測，預測模型對不同壽命段的采樣數據均具有較好的預測效果，所有的壽命預測結果在2倍誤差帶以內，絕大部分的壽命預測結果在1.5倍誤差帶以內。

(3)相較于總應變能密度，選取平均應變的變化作為損傷變量所得損傷曲線具有更好的代表性，可以較好地反映載荷對疲勞損傷的影響，與實測損傷點的符合程度更好，同時，以平均應變的變化作為損傷變量的低周疲勞壽命預測模型的預測效果也更好。