光刻機工件臺解耦矩陣校準測試方法研究

汪杰君，王劍峰，張志鋼

（1.桂林電子科技大學，廣西 桂林 541000；2.上海微電子裝備（集團）股份有限公司，上海 200120）

0 引言

自1973年第一臺光刻機在荷蘭問世以來，光刻機的伺服精度與日提高，現在已取得了長足的發展[1,2]。光刻機的主要系統包括：光學系統、機械減震系統、測量反饋系統、工件臺和掩模臺系統等[3]。超精密工件臺作為光刻機的3大關鍵技術之一[4]，其要求具有納米級的定位精度和同步運動精度[5,6]。由于工件臺的制造工藝、非質心驅動和測量反饋裝置的原因，工件臺的實際位置和目標位置存在一定的誤差，因而采用合理的測校技術對工件臺一些參數進行校準，成為改善其定位精度和同步運動精度的主要手段[7]。

1 光刻機工件臺解耦的基本原理分析

圖1 音圈電機布局示意圖Fig.1 Diagram of sound coil motor layout

工件臺主要由3大部分組成：基礎框架、平衡質量塊、粗微動臺體，微動臺是光刻機的核心部件，是微動臺進行納米級運動的關鍵，刻片時微動臺通過調平、調焦等動作，并進行納米級的曝光運動，使硅片晶圓完整。微動臺按功能分為4個機構：Chuck部件、執行機構、測量機構、E-Pin部件曝光。Chuck部件主要包括45°微晶鏡塊和真空吸盤。45°微晶鏡塊作為反射鏡，配合雙頻激光干涉儀進行高精度測量；真空吸盤用來固定硅片，防止在上下片過程中硅片滑落；另外，Chuck部件裝載測量宏微相對位置傳感器的磁極，執行機構主要包括微動平面音圈電機本體及垂向音圈電機。執行機構采用3個平面音圈電機實現執行機構動子的水平X、Y向運動以及Rz偏轉；采用3個垂向音圈電機實現執行機構動子的垂向Z向運動和Rx、Ry偏轉，這樣可實現微動臺六自由度精密運動控制；另外，臺體垂直方向上還安裝重力補償器，用來抵消微動臺重力，來減少音圈電機出力，6個音圈電機布局示意圖如圖1所示。因此，由于微動電機六自由度的存在，并且其結構精密，系統復雜，不可避免地存在耦合現象，且耦合會影響工件臺的工作效率、套刻精度。如果不考慮耦合作用來設計控制系統，在實際中往往會帶來很大的控制偏差，所以需要對其進行解耦[8,9]。

2 工件臺GB解耦矩陣校準的建模分析

2.1 微動臺與音圈電機的力學關系解耦分析

如果將微動臺看做一個整體，在控制微動臺體沿著某個方向平移，或沿著質心坐標系的某個軸做旋轉時，需要由控制系統計算出所需要的力或力矩的大小，并能夠恰當地控制各個電機，使得它們的合力恰好是所需要的，這樣可以對應每個自由度的位移或轉角設計各個自由度的閉環控制系統，各自閉環系統的輸出其物理含義是對應的力或力矩大小。磁浮平面電機可分為6個物理軸，分別為H1，H2，H3，Z1，Z2，Z3，它們的相互作用可使電機產生6個自由度的運動。其中，物理軸H1，H2，H3產生水平X向和Y向運動，Z1，Z2，Z3產生垂直Z向運動，水平向和垂直向的相互作用產生旋轉運動。當電機在X向和Y向出力時，存在從控制中心到質心點的增益規劃和從質心點到執行器的增益平衡。工件臺微動臺在質心坐標系下和幾何坐標系下的受力模型如圖2所示。

圖2 微動臺質心坐標系下的微動臺受力示意圖Fig.2 Diagram of the force of the microdynamic table under the centroid coordinate system of the micro-actuator

Fh2和Fh3與X軸的夾角為60°，3個水平向矢量電機內切圓半徑為R，Fh2與內切圓切點、內切圓圓心和微動臺質心3點共線。從圖2可以得出，磁浮平面電機動子在水平向由3組三相線圈驅動，實現X，Y，RZ三自由度運動。其中，力Fh1和Fh2，Fh3實現X和Y向驅動，Fh1和Fh2，Fh3差動實現RZ的運動。垂向由同樣3組三相線圈驅動，實現Z，Rx，Ry三自由度運動。其中，FZ1，FZ2，FZ3實現Z向驅動，Fh1和Fh2，Fh3，FZ1，FZ2，FZ3差動實現Rx向和Ry向驅動。對于平面電機動子質心處的邏輯力及力矩同物理軸各電機驅動力關系可如公式（1）所示：

GB逆矩陣如公式（2）所示：

圖4 MIMO系統的控制器模塊圖Fig.4 Controller module diagram of MIMO system

圖3 短程電機輸入輸出Fig.3 Short-range motor input and output

GB逆矩陣參數配置只能用于工件臺的理想模型，實際上由于制造誤差，如果要求高控制性能，這個矩陣不準確，只能用作默認設置。該矩陣的36個元素均需要進行校準。

2.2 GB解耦矩陣校準算法研究

2.2.1 過程傳函計算方法分析

GB解耦矩陣的作用是將邏輯軸控制器的輸出力轉換到各個物理軸上。SI表示輸入敏感度傳函（輸入為u，輸出為in，見圖3），SP表示過程傳函（輸入為u，輸出為out，P表示in和out之間的傳函），則in和out處的輸出分別為：

由式（3）、式（4）可得：

2.2.2 機械傳涵計算方法分析

工件臺伺服控制環路描述如圖4所示。

由圖4可知：Raw Mechanics表示B點到C點之間的過程傳函，Compensated Mechanics表示A點到C點之間的過程傳函，A點到B點之間的過程傳函即為GS矩陣與GB矩陣的乘積。因此，GB矩陣可通過計算Hmraw（原始機械傳函）、Hmc（補償機械傳函）和GS矩陣來獲取。

1）計算機械傳函

利用2.2.1所描述的過程傳函計算方法可分別計算Hmraw和Hmc。

原始機械傳函與補償機械傳函的關系如下：

其中，GBnom為校準前的GB矩陣。

2）計算理想機械傳函和GS0矩陣

校準后補償機械傳函應該等于一固定的傳函Hmd

其中，GBcal為校準后的GB矩陣，Hmd和Gs0（Gs0表示工件臺處于零位時微動臺作用點與質心之間的轉換關系）計算公式如下：

Gs0為：

其中，xstep、ystep、zstep為工件臺在原點時名義重心相對測量點的位移，xcog、ycog、zcog為工件臺在原點時名義重心相對實際重心的位移，其具體值由機器常數給定。

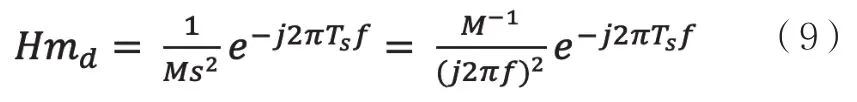
其中，M為：

其中，Mass為Chuck質量；Jzz為Chuck繞Z軸旋轉的轉動慣量；Jxx為Chuck繞X軸旋轉的轉動慣量；Jyy為Chuck繞Y軸旋轉的轉動慣量；Ts為采樣周期。

3）計算GB矩陣

當原始機械傳函確定后，校準后的GB矩陣可表示為：

由式（7）和式（11）可得GB的校準公式如下：

且GB校準矩陣需取某一頻率段的均值，該頻率范圍是[20Hz，50Hz]。

3 實驗數據分析

校準前，通過機器常數獲取的GB矩陣的值為：

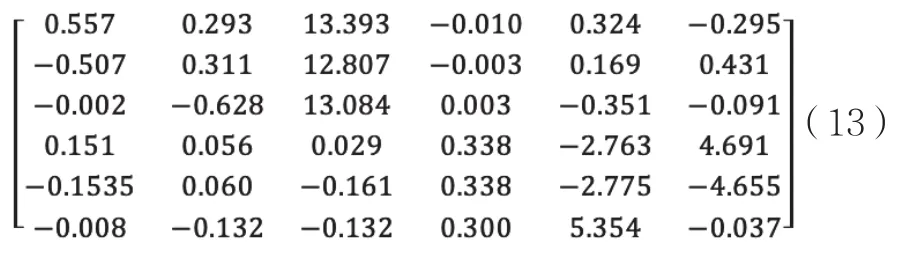
校準后的GB矩陣，如式（14）所示：

在頻域上進行分析測試。

如圖5所示，當對X軸注入噪聲，噪聲水平為20Hz～50Hz時，校準后的機械傳涵幅值大幅度降低，即GB解耦矩陣校準后，X方向對RY方向的串擾顯著降低。

圖5 X軸注入噪聲，在RY方向上校準前后的串擾對比Fig.5 X-axis injection noise, crosstalk contrast before and after calibration in RY direction

圖6 Y軸注入噪聲，在RX方向上校準前后的串擾對比Fig.6 Y axis injection noise, crosstalk contrast before and after calibration in RX direction

圖7 Y軸注入噪聲，在X方向上校準前后的串擾對比Fig.7 Y axis injection noise, crosstalk comparison before and after calibration in X direction

如圖6所示，當對Y軸注入噪聲，噪聲水平為20Hz～50Hz時，校準后的機械傳涵幅值大幅度降低，即GB解耦矩陣校準后，X方向對RY方向的串擾顯著降低。

圖8 RX軸注入噪聲，在Y方向上校準前后的串擾對比Fig.8 Rx axis Injection noise, crosstalk contrast before and after calibration in Y direction

如圖7所示，當對Y軸注入噪聲，噪聲水平為20Hz～50Hz時，在X方向上校準后的機械傳涵幅值明顯降低，即GB解耦矩陣校準后，Y方向對X方向的串擾顯著降低。

如圖8所示，當對RX軸注入噪聲，噪聲水平為20Hz～50Hz時，在Y方向上校準后的機械傳涵幅值明顯降低，即GB解耦矩陣校準后，RX方向對Y方向的串擾顯著降低。

如圖9所示，當對Z軸注入噪聲，噪聲水平為20Hz～50Hz時，校準后的機械傳涵幅值大幅度降低，即GB解耦矩陣校準后，Z方向對RX方向的串擾顯著降低。

4 結論

本文主要研究工件臺微動臺GB解耦矩陣的測校方法。根據工件臺結構特點，分析得出六自由度之間的耦合會影響工件臺的工作效率、套刻精度，在微動臺與音圈電機的力學層面分析, 給出了具體的解耦關系式，然后對微動GB解耦矩陣校準方法進行了研究。從工件臺的伺服控制環路上的機械傳涵為出發點，設計了傳遞函數法對微動臺GB解耦矩陣校準方案，根據最終測試數據，頻域上分析得出工件臺微動各軸之間的串擾有著明顯降低，很好地滿足了課題的需要，驗證了方法的有效性。

圖9 Z軸注入噪聲，在RX方向上校準前后的串擾對比Fig.9 Z axis injection noise, crosstalk contrast before and after calibration in RX direction