不同飛行軌跡對旋翼斜下降狀態噪聲影響計算分析

2019-04-10 09:30:10袁明川劉平安林永峰

直升機技術 2019年1期

袁明川，劉平安，樊楓，孫偉，林永峰

(中國直升機設計研究所直升機旋翼動力學重點實驗室，江西景德鎮 333001)

0 引言

直升機一般在低空域飛行，噪聲水平過高是其在應用中需重點關注的問題。在軍用領域，直升機遠場噪聲使其在戰場上容易暴露目標，影響其聲隱身特性及突襲能力。在民用領域，直升機噪聲影響城市環境及居民生活，民航的適航標準CCAR-36中對直升機噪聲水平具有嚴格的限制。旋翼噪聲，特別是旋翼BVI噪聲，是直升機在常規飛行速度下最為強烈的噪聲源。BVI噪聲由旋翼槳葉和槳尖渦相互干擾引起的壓力劇烈變化產生，聲壓呈現脈沖特征，幅值大且頻域分布寬[1-3]。對于給定的直升機飛行任務，不同的飛行軌跡下旋翼槳-渦干擾情況差異很大，BVI噪聲的輻射強度和傳播指向性也并不相同。針對不同飛行軌跡對旋翼遠場噪聲輻射特性的影響進行研究，對于直升機噪聲水平控制具有重要的實際應用意義。

國外針對旋翼類飛行器的飛行軌跡噪聲控制進行了初步的參數影響分析。美國馬里蘭大學的Gervais和Schmitz分別針對傾轉旋翼機和直升機，研究了不同飛行軌跡和操縱策略對BVI噪聲的影響[4,5]。Gervais通過槳-渦干擾距離的變化來表征BVI噪聲控制效果，Schmitz采用準定常聲輻射圖(Q-SAM)進行直升機遠場噪聲預測，二者均未直接進行旋翼噪聲的計算。在國內，南京航空航天大學的徐國華和中國直升機設計研究所的林永峰等對旋翼噪聲進行了大量的數值計算和少量試驗研究[6,7]，然而針對直升機飛行軌跡控制對噪聲影響的研究開展很少。國內旋翼噪聲計算主要采用CFD結合FW-H方程的方法，需指出，CFD計算時槳尖渦數值耗散降低了BVI噪聲的預測精度，且現有條件下CFD計算效率難以滿足旋翼配平需求。

本文采用Camrad Ⅱ的自由尾跡模型進行旋翼非定常氣動計算[8]，基于Farassat 1A方程進行旋翼氣動噪聲求解[9]。采用BO-105旋翼建立噪聲計算模型，針對直升機的斜下降飛行任務，對比了不同飛行軌跡中旋翼噪聲的傳播特性，并分析了不同飛行軌跡中飛行狀態的改變對旋翼配平操縱及BVI噪聲輻射的影響。進一步改變了旋翼飛行速度，對比了旋翼狀態變化對不同軌跡噪聲傳播的影響。

1 計算方法

1.1 噪聲計算方法

采用直升機綜合分析軟件Camrad Ⅱ進行旋翼非定常氣動載荷計算，計算中考慮氣動和結構的耦合。氣動計算采用Scully自由尾跡模型，將尾跡分為近尾跡和遠尾跡分別處理，近尾跡區域充分考慮附著渦和尾渦的影響，遠尾跡區主要考慮槳尖渦誘導作用，由近尾跡過渡至遠尾跡的渦齡角為60°。考慮到槳尖渦附近誘導速度計算存在奇異性，采用渦核模型對槳尖渦進行模擬。旋翼動力學建模中，槳轂采用多體動力學模型，槳葉采用梁單元模型，計算中只考慮槳葉揮舞和變距運動。旋翼噪聲計算以槳葉非定常載荷(槳葉剖面的升力系數、阻力系數和馬赫數)以及槳葉揮舞和變距運動數據作為輸入參數，其中槳葉運動以諧波形式輸入，只考慮二階以下的運動。旋翼噪聲數值計算基于Farassat 1A方程，如式(1)和(2)所示。

(1)

(2)

1.2 旋翼配平

為了保證直升機在飛行中處于力和力矩的平衡狀態，在計算中需要對旋翼進行配平。旋翼配平的目標為全機重力和阻力平衡，同時保證俯仰力矩和滾轉力矩為0。旋翼配平所需的操縱量為總距、縱/橫向周期變距和軸傾角。配平計算通過牛頓下山法迭代收斂。

1.3 計算和試驗對比

采用BO105旋翼模型風洞試驗數據[10]對氣動噪聲計算方法進行了對比驗證。試驗狀態為產生強烈BVI噪聲的斜下降飛行狀態，旋翼槳尖馬赫數為0.64，前進比0.151，軸傾角3.9°。噪聲測點距離旋翼中心1.39R，方位角133°，與槳盤平面夾角57°。圖1為旋翼聲壓時間歷程計算值和試驗值的對比。從對比結果可以看出，計算獲得的BVI脈沖噪聲結果和試驗結果具有良好的一致性。

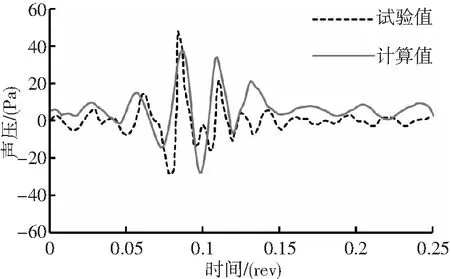
圖1 計算和試驗對比

1.4 飛行軌跡及噪聲測點

圖2為三種不同的飛行軌跡數示意。三種飛行軌跡具有相同的起始和終止位置。軌跡1從起點直接通過下降6°飛行達到中終止點；軌跡2先進行水平飛行，然后斜下降9°飛行達到終點；軌跡3首先進行斜下降9°飛行，然后水平飛行到達終點。噪聲測點1、2、3位于飛行終點的下方，其中測點1位于縱向剖面右側100m，測點2位于縱向剖面內，測點3位于縱向剖面左側100m。

圖2 飛行軌跡與噪聲觀測點示意

1.5 計算模型和計算狀態

采用BO105全尺寸旋翼建立噪聲計算分析模型，旋翼具體參數見表1。在實際計算中，由于無法獲得BO-105槳葉的詳細結構數據，因而采用偏置揮舞鉸加彈性約束的方式等效處理槳葉結構模型，通過調節揮舞鉸的位置和剛度獲得給定的揮舞一階頻率1.12[11]。主要計算了水平飛行、6°斜下降飛行和9°斜下降飛行三種狀態，旋翼前進比為0.15。計算時全機重量配平目標為2200kg，阻力配平目標由阻力面積給定，阻力面積CxS=1.32m2。

表1 計算模型參數

2 計算結果對比分析

2.1 不同飛行軌跡旋翼噪聲傳播對比

圖3給出了直升機在不同軌跡的整個飛行過程中不同噪聲測點處A計權總聲壓級的對比結果。對比不同測點的噪聲特性，可以看出測點1和2的噪聲輻射強度明顯大于測點3。這是因為測點1位于旋翼前行側，BVI噪聲在該區域內具有明顯的傳播指向性，而測點2的噪聲傳播距離最小，因而噪聲更強。在后續分析中重點關注測點1和2的噪聲特性。對比不同飛行軌跡，可以看出不同飛行軌跡下旋翼噪聲的傳播特性并不相同，軌跡2和軌跡3相對軌跡1具有明顯的噪聲降低效果，特別是采用軌跡3的整個飛行過程中的最大A計權總聲壓級在測點2降低大約6dB。

圖4給出了測點2的噪聲變化曲線中點A與點B聲壓時間歷程的對比，從中可以明顯看到脈沖噪聲信號的減弱。這說明不同飛行軌跡下噪聲傳播特性的變化主要是由于旋翼狀態的改變影響了BVI噪聲的強度和指向性，進而實現了遠場噪聲的有效降低。

2.2 不同飛行狀態噪聲特性特性分析

文中的飛行軌跡由水平飛行、6°斜下降和9°斜下降三種飛行狀態組成。本章節對比了這三種飛行狀態的配平操縱和槳-渦干擾特性以及不同方位角和不同槳盤平面夾角的噪聲傳播指向性，分析了不同飛行狀態組合對飛行軌跡噪聲控制的內在影響。

圖3 不同飛行軌跡旋翼總聲壓級對比(μ=0.15)

圖4 飛行軌跡3中點A，B聲壓時間歷程

槳-渦干擾距離是對旋翼BVI噪聲產生和傳播的主要影響因素。圖5給出了在前行側發生平行干擾(60～90°方位角范圍)時槳葉和自身產生的槳尖渦以及和上一片槳葉產生的槳尖渦的干擾距離的對比情況，圖中干擾距離為正表示槳尖渦位于槳葉上方。從圖中可以看出，水平飛行時槳尖渦基本位于槳葉下方，斜下降飛行時槳尖渦逐漸向上移動，6°斜下降狀態的槳尖渦移動到靠近槳葉的區域，9°斜下降狀態的槳尖渦繼續向上移動，反而造成槳-渦干擾距離的增加。

圖5 不同飛行狀態旋翼槳-渦干擾距離對比

表2給出了不同飛行狀態下的旋翼操縱量配平結果。從中可以看出，水平飛行時通過旋翼前傾(軸傾角為負)克服直升機阻力，此時旋翼前方來流存在垂直槳盤的向下分量，造成槳尖渦更快地向下移動。在斜下降狀態，旋翼后傾平衡重力沿速度方向的分量，旋翼存在向上的入流，造成槳尖渦向上移動。這和圖5中槳-渦干擾距離變化相一致。

圖6為三種飛行狀態下旋翼噪聲在不同方位角和不同槳盤夾角的傳播特性對比。從中可以看出，6°斜下降飛行的噪聲水平明顯大于另外兩種飛行狀態，這主要是因為槳-渦干擾距離的減小產生了強烈的BVI噪聲。對比圖6(a)中不同方位角的噪聲傳播特性，可以看出在前行側(90°～180°方位角)范圍內水平飛行狀態的噪聲最小，這解釋了圖3(a)中軌跡3飛行狀態改變時的噪聲劇烈下降。對比圖6(b)中不同槳盤夾角的噪聲傳播特性，可以看出在55°夾角之前9°斜下降狀態噪聲最小，55°之后水平飛行噪聲最小，這解釋了圖3(b)中軌跡3整個飛行過程中最大噪聲的大幅度降低。

表2 不同飛行狀態旋翼操縱量計算值(μ=0.15)

圖6 不同飛行狀態噪聲傳播指向性

2.3 不同飛行速度下噪聲傳播特性

旋翼飛行狀態參數的改變影響旋翼的槳-渦干擾情況，進而影響BVI噪聲的產生和傳播。改變了旋翼的飛行速度，對比了旋翼飛行速度變化后不同飛行軌跡對旋翼噪聲傳播特性的影響。

圖7為前進比0.18時測點1和2處的A計權總聲壓級變化。對于測點1，采用軌跡1飛行時旋翼最大總聲壓級最小，這和圖3的計算結果并不相同。對于測點2，采用軌跡3飛行仍然降低了旋翼噪聲輻射強度，但是噪聲降低幅值只有3dB左右。表3給出了前進比改變后旋翼的操縱量配平結果，可以看出旋翼軸傾角相對于前進比0.15狀態具有明顯變化。飛行速度和軸傾角的改變共同影響了旋翼槳-渦干擾狀態，進而造成了BVI噪聲輻射特性的變化，影響了飛行軌跡的噪聲控制效果。