一個多維次成分并行提取算法及其收斂性分析

董海迪 何兵 劉剛 鄭建飛

在信號處理領域,將信號自相關矩陣最小特征值對應的特征向量定義為信號的次成分(Minor component,MC).次成分分析是一種從信號提取次成分的技術.次成分分析已經廣泛應用于計算機視覺[1]、波達方向估計[2]、FIR濾波器設計[3]、曲面擬合[4]等領域.目前,基于神經網絡的次成分分析算法是國際上的一個研究熱點.相比傳統的特征值分解算法,神經網絡算法具有計算復雜度低、能夠在線實施和跟蹤非平穩信號等優點[5].

根據提取次成分的維數,次成分分析算法可以分為:單維次成分提取、次子空間跟蹤和多維次成分提取等三類[6].目前,學者們已經提出了大量的單維次成分提取算法和次子空間跟蹤算法[2?3,6],而多維次成分提取算法還非常稀少.傳統的多維次成分提取大多是通過串行提取或空間旋轉來實現[6].串行提取法是首先利用單維次成分分析算法提取信號的第一個次成分,然后利用膨脹技術依次提取下一個次成分.串行算法的缺點在于存儲器需求量大、提取時間有延遲、誤差累計傳播等.空間旋轉法是首先利用次子空間跟蹤算法提取信號的次子空間,然后進行空間旋轉得到多維次成分.空間旋轉法的缺點在于計算復雜度的增加[7].

相比串行提取法和空間旋轉法,并行算法能夠直接從信號中提取多維次成分,且不需要中間轉換過程,因此可以避免兩類算法的缺點.最早的并行提取算法是由芬蘭學者Oja提出來的[8],該算法雖然可以并行提取多維次成分,但是其要求信號的最小特征值必須小于1;Mathew等提出的算法[9]雖然沒有特征值大小的限制,但是該算法只適用于信號具有多個相同的最小特征值;基于Douglas次子空間跟蹤算法,Jankovic等[10]提出了一種新型多維次成分提取算法—MDouglas算法,雖然該算法對特征值大小沒有要求,但是需要事先選取參數,而且該參數選取的結果直接影響著算法的收斂性能;采用主/次成分轉換機制,Tan等提出了一種并行提取算法[11],該算法的缺點在于需要事先對最小特征值進行估計;Bartelmaos等所提出的MCA-OOJAH算法[12]雖然對信號特征值沒有要求,但是需要在每次迭代過程中增加模值歸一化措施,以保證算法的收斂性.頻繁的模值歸一化操作極大地增加了MCA-OOJAH算法的計算復雜度.綜上所述可得,現有算法存在以下幾個方面的問題:1)對信號的特征值有要求;2)需要事先選取一些參數;3)算法計算過程復雜.本文研究目的就是發展能夠避免上述缺點的多維次成分并行提取算法.

本文的主要貢獻可以歸納為以下三個方面:1)提出了一種多維次成分并行提取算法,該算法對信號的特征值沒有要求,而且不需要模值歸一化操作;2)利用遞歸最小二乘(Recursive least square,RLS)技術對所提算法進行改進,導出了一種具有低計算復雜度的算法;3)利用李雅普諾夫函數法完成了對所提算法的全局收斂性分析,確定了所提算法的全局收斂域.

論文的結構安排如下:第1節是對神經網絡模型和次成分進行簡介;第2節是在研究OJAm算法的基礎上,提出兩種多維次成分提取算法;第3節是采用李雅普諾夫函數法對所提算法的全局收斂性進行證明;第4節是通過仿真實驗對所提算法的性能進行驗證;論文的總結安排在第5節.

1 問題描述

考慮如下一個具有多輸入多輸出的神經網絡模型:

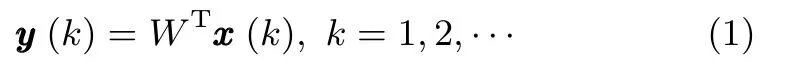
其中,y(k)∈Rr×1是神經網絡的輸出,W∈Rn×r是神經網絡的狀態矩陣,輸入信號x(k)∈Rn×1是一個零均值的隨機過程,這里作為神經網絡的輸入,n為輸入向量的維數,r為所需提取次成分成分的維數.

令R=E[x(k)xT(k)]為輸入信號x(k)的自相關矩陣,λi和ui(i=1,2,···,n)分別為自相關矩陣R的特征值和對應的特征向量.根據矩陣理論可得:矩陣R是一個對稱非負定矩陣,且其特征值均是非負的.為了后續方便,這里將其矩陣R的特征值按照從大到小方式排列,即

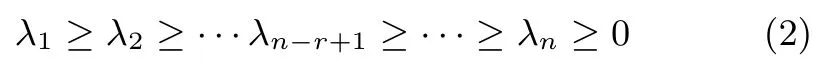
則矩陣R的特征值分解可以表示為

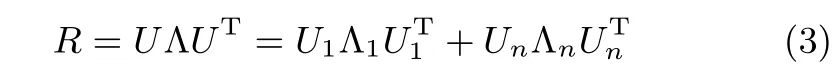
其中,U=[u1, u2,···, un]是由矩陣R的特征向量構成的矩陣,Λ=diag{λ1,λ2,···,λn}是由矩陣R的特征值構成的對角矩陣,U1=[u1,u2,···,un?r]是由前n?r個特征向量構成的矩陣,Λ1=diag{λ1,λ2,···,λn?r}是由前n?r個特征值構成的對角矩陣,Un=[un?r+1,un?r+2,···, un]和Λn=diag{λn?r+1,λn?r+2,···,λn}分別為后r個特征向量和特征值構成的矩陣.

根據定義可知特征值λn?r+1,λn?r+2,···,λn所對應的特征向量un?r+1, un?r+2,···,un稱為信號的前r個次成分,而由特征向量un?r+1,un?r+2,···,un張成的子空間V1=Span{ un?r+1, un?r+2,···, un}稱為信號的次子空間.子空間跟蹤算法的目的是能夠估計出子空間V1的一組基,而多維次成分提取算法則是要找到確定的特征向量un?r+1, un?r+2,···,un.

2 多維次成分并行提取算法

2.1 多維次成分提取算法的提出

在文獻[13]中,Feng等提出了OJAm次子空間跟蹤算法.當OJAm算法收斂時,該算法的狀態矩陣只能收斂到信號次子空間的一組正交基,而非多維次成分.通過對OJAm算法進行加權處理,這里提出如下算法

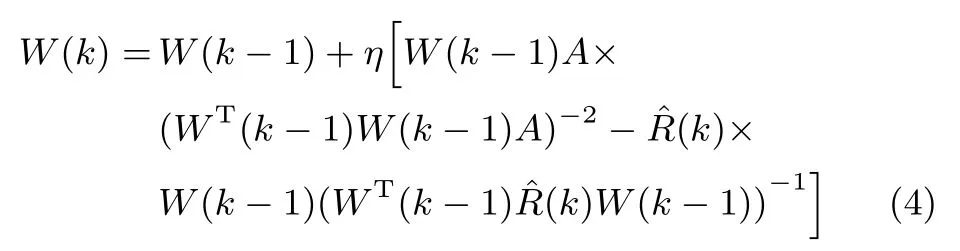
其中,η是神經網絡的學習因子,滿足關系:0<η≤1;A=diag{a1,a2,···,ar}是一個r×r維對角矩陣,其對角線元素均為正數,且滿足關系:ar>ar?1>···>a1>0;(k)為k時刻對自相關矩陣R的估計值,即

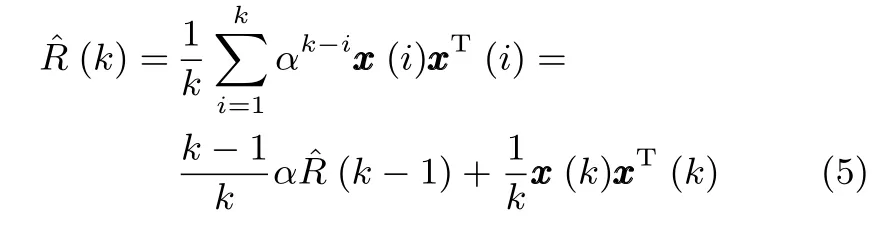
其中,α被稱為遺忘因子.如果樣本來自于一個平穩的隨機過程,則可以令α=1,此時式(5)相當于對x(k)xT(k)取瞬時數學期望.顯然當訓練樣本非常大時,(k)將等價于自相關矩陣R.另一方面,如果x(k)取自一個非平穩的隨機過程,則遺忘因子α應該在區間(0,1)內取值,以便對采樣樣本施加一個寬度為1/(1?α)的遺忘窗.該遺忘窗通過對不同時刻的采樣樣本賦予不同的權值來降低以往數據對于當前結果的影響.遺忘因子α的取值是由采樣信號來決定.通常對于變化緩慢的樣本,α的取值要接近1以產生一個較大的遺忘窗;而對于變化快速的樣本,遺忘窗口寬度應比較小,此時α則應該在接近0處取值[14].為了方便后續使用,這里將式(4)所描述的算法記為WOJAm(Weighted OJAm)算法.

從式(4)可得:學習因子η控制著算法的學習步長.一般說來,學習因子η越大,算法的學習步長越大,算法的收斂速度也越快,但是學習因子過大有時會引起算法的震蕩甚至發散.反之,學習因子越小,算法的學習步長越小,收斂速度也越慢,因此過小的學習因子會降低算法的性能.目前,學習因子的選擇主要依靠經驗知識,如何選取最優的學習因子仍是一個難以解決的問題.從式(5)可得:遺忘因子主要影響著信號的自相關矩陣.根據文獻[15]的研究,遺忘因子對于算法的收斂速度幾乎沒有影響.

2.2 基于遞歸最小二乘的改進型算法

雖然WOJAm算法可以提取信號的多維次成分,但其計算復雜度為n2r+5nr2+11r3/3,高于OJAm算法n2r+2nr2+10r3/3的計算算復雜度.通常,高昂的計算復雜度會在一定程度上限制算法的使用范圍.由于RLS技術能夠在不改變算法性能的前提下降低算法的計算復雜度[16],因此本節將研究基于RLS技術的多維次成分提取算法.

假設在第i(1≤i≤k)次迭代時,輸入數據x(i)在神經網絡狀態矩陣W(k?1)上的投影可以通過式y(i)≈WT(i?1)x(i)來近似(這一近似已經廣泛應用于很多算法的推導過程中,并不會影響算法的最終性能[17]).通過這一近似,就可以在任意時刻i(i=1,2,···,k)獲得神經網絡的輸出y(i)的估計值.將式(5)代入式(4)可得:

為了方便計算,這里做如下簡記:

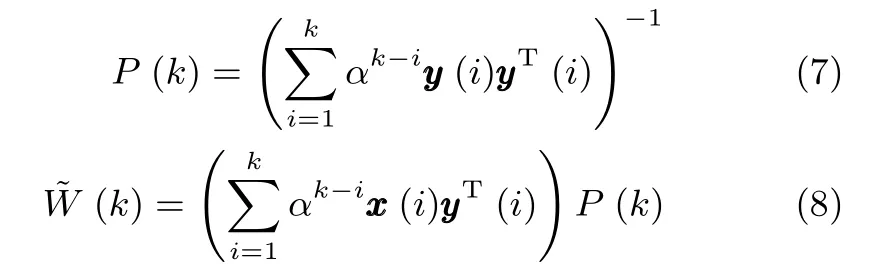
應用矩陣求逆引理[18],則式(7)可以化簡為:

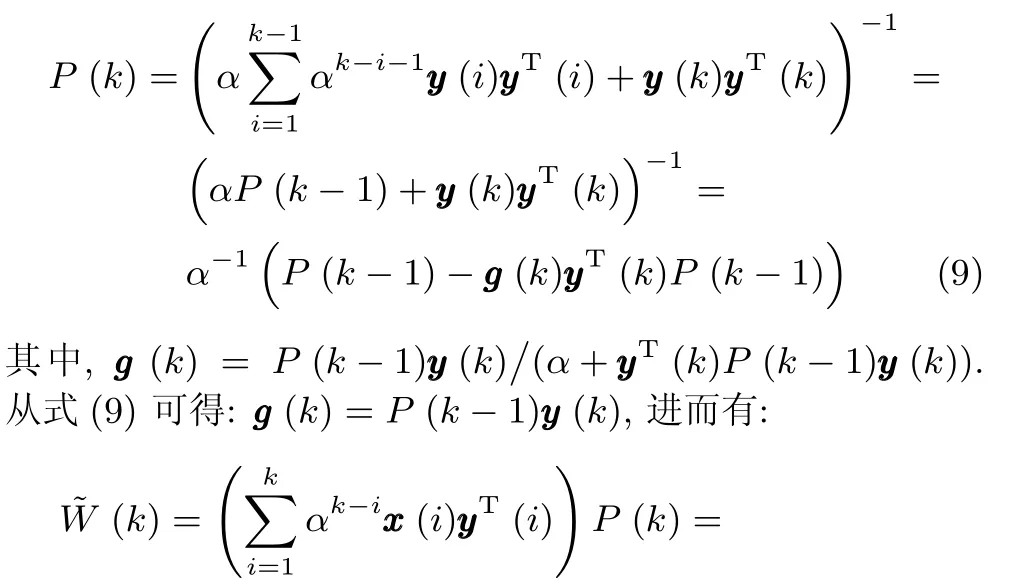
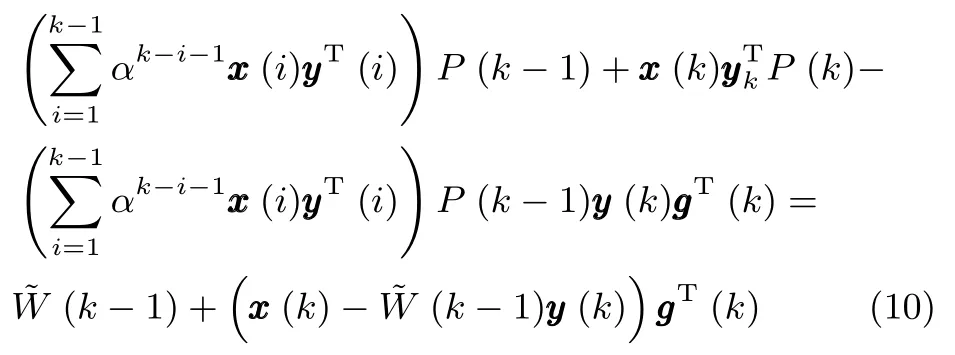
上式推導過程中用到了如下結論:

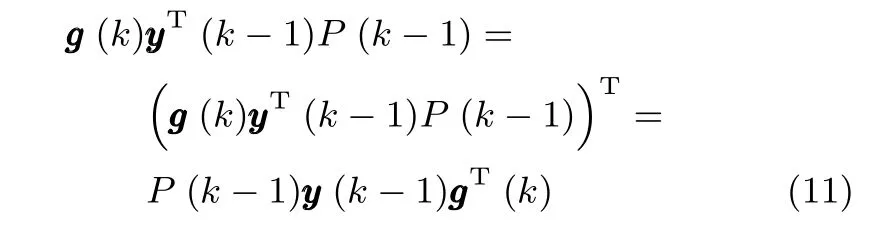
綜合式(6)～(10),就可以利用k時刻的輸入向量x(k)和k?1時刻的(k?1)來估計狀態矩陣(k),即完成了利用RLS技術對WOJAm算法的改進,因此將該算法記為RLS-WOJAm算法,其計算過程如下.

初始化:令k=0,選擇合適的學習因子η和遺忘因子α,其他初始化參數設置為:P(0)=δIr(其中δ是一個非常小的數),(0)=0.

迭代過程:令k=k+1,根據以下方程對神經網絡狀態矩陣進行更新迭代,

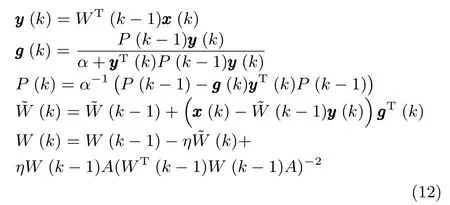
2.3 算法性能評價

本節對所提算法進行分析,并將所提算法與一些現有算法進行比較:

1)將WOJAm算法與OJAm算法進行對比可以發現,兩者相差的只是加權矩陣A.OJAm算法只是在對狀態矩陣的模值進行了約束,而WOJAm算法則是通過該加權矩陣對狀態矩陣不斷地實施Gram-Schmidt正交化操作,從而使得狀態矩陣能夠收斂到所需的次成分.顯然,這里加權矩陣的作用是與文獻[16]相類似的.

2)從文獻[13]可得,OJAm 算法是一個次子空間跟蹤算法,算法只能收斂到信號次子空間V1=Span{ un?r+1,un?r+2,···, un}的一組基,不一定是次成分un?r+1, un?r+2,···,un,而所提算法收斂結果則是確定的次成分.根據矩陣理論[18]可得:子空間V1有很多種不同的基,而次成分只是其中一個特殊的基.即所提算法不僅適用于多維次成分提取,而且還可以用于子空間跟蹤.因此相比OJAm算法,所提算法具有更為廣泛的應用范圍.

3)這里將所提算法與近期提出的AMMD算法[11]和MCA-OOJAH算法[12]進行對比.在應用AMMD算法前,必須要對信號自相關矩陣的最大特征值進行估計,由于信號是多種多樣,有些情況下是難以估計的,因此這一約束限制了AMMD算法的實際應用.而所提算法在使用前并沒有這一要求,因此拓寬了使用范圍.MCA-OOJAH算法雖然沒有限制條件,但是其需要在每一次迭代過程中增加狀態矩陣模值歸一化操作,以確保算法的穩定性,由于大量的歸一化操作,增加了MCA-OOJAH算法的計算量,而所提算法則沒有這些要求,降低了算法的硬件開銷.

4)雖然WOJAm算法的計算復雜度為n2r+5nr2+O(n),但是由其導出的RLS-WOJAm算法的計算復雜度將至2nr2+2nr+O(n).這一計算復雜度不僅要低于原來的OJAm次子空間跟蹤算法(n2r+2nr2+10r3/3),而且還要比AMMD算法[11]n3+2n2r+O(n)的計算復雜度和MDouglas算法[10]n2r+5nr2+O(n)的計算復雜度要低很多.此外,RLS-WOJAm算法只涉及到矩陣的加、乘和簡單求逆操作,因此實施較為容易.

3 算法的全局收斂性分析

文獻[13]只是對OJAm算法進行了收斂性分析,并未給出算法的收斂域;本節將通過李雅普諾夫函數法對所提算法的收斂性進行分析,確定出算法的收斂域.借鑒現有文獻[19]分析結論可得:所提WOJAm算法和RLS-WOJAm在本質上是相同的,因此兩個算法具有相同的全局收斂域.假定輸入信號x(k)是一個零均值的平穩隨機過程,當學習因子η非常小時,根據隨機近似理論[20],則式(4)所描述的離散時間方程可以轉化為相對應的一階常微分方程

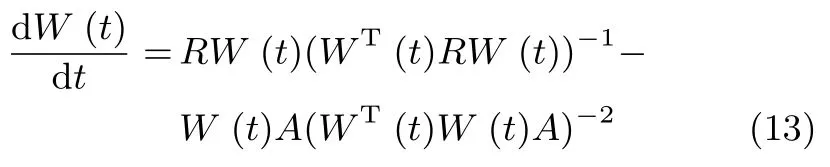
其中,t=μk.通過對式(13)的收斂性分析就可以間接獲得所提算法的全局收斂性.事實上,算法的全局收斂性主要是回答以下兩個問題[21]:

1)式(13)所描述的動態系統能否全局收斂到自相關矩陣的多維次成分?

2)算法對于次成分的吸引域是多少?或者說確保算法全局收斂的初始條件是什么?

為了回答上述問題,這里構造如下函數:

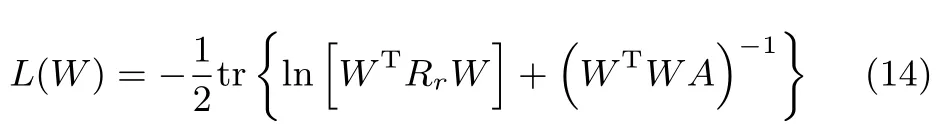
其中,Rr=UnΛnUTn.所提算法的收斂性可以通過定理1來完成.

定理1.L(W)是常微分方程(13)所對應的李雅普諾夫函數,通過該函數可以獲得神經網絡狀態矩陣W在平穩點處的吸引域為

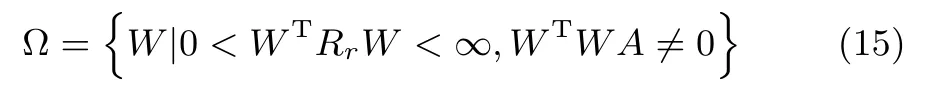
證明.由于L(W)是一個連續函數,則其是連續可微的:

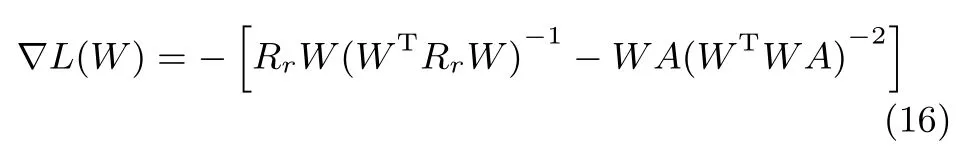
通過鏈式法則,可以獲得L(W)對于時間t的導數

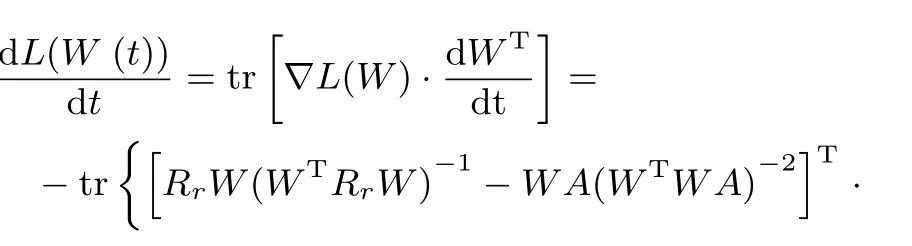
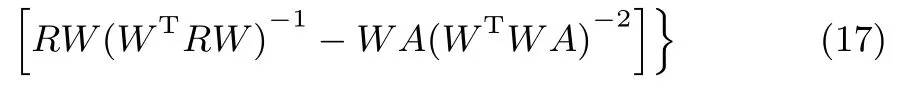
為了方便起見,上式中省略了時間變量t.根據李雅普諾夫第二定律,需要證明如下結論:在域,而在域內(dL(W)/dt)=0.為了完成上述證明,這里將R=代入式(17),并進行適當化簡可得:

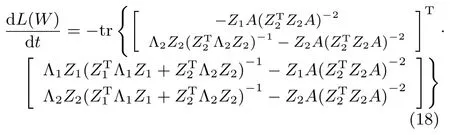
其中,Z1=UT1W和Z2=UTnW.由于WTRrW0,則矩陣Z2是可逆的.因此,必定存在一矩陣B∈R(n?r)×r使得Z1=BZ2成立.將式(18)中的Z1用Z2來表示,則有:

其中,C=(Z2TZ2)?1A?1(Z2TZ2)?1.當W接近平穩點處時,矩陣C可以近似為一個對角矩陣,即C≈C′=diag{c1,c2,···,cr}.此時,式(19)就可以化簡為:

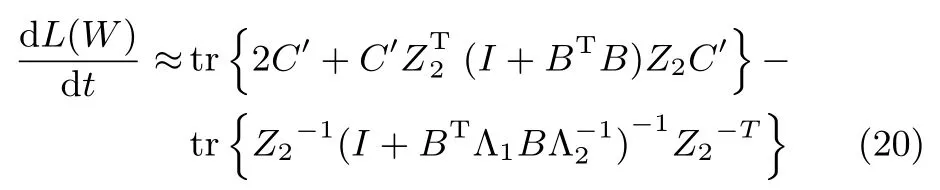
接下來,考慮矩陣Z10的情況.根據矩陣理論有:

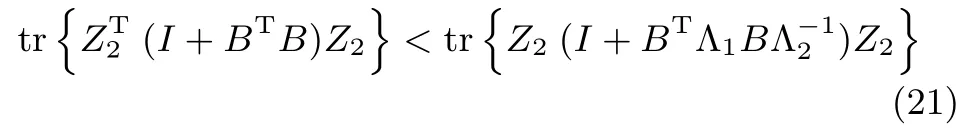
令D=ZT2(I+BTB)Z2,則其特征值分解可以表示為:

其中,Ψ=diag{μ1,μ2,···,μr}是一對角矩陣,μi(i=1,2,···,r)是矩陣D的特征值,Φ是由特征向量組成的矩陣.將式(22)代入式(21)可得:

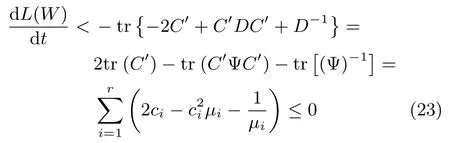
接下來考慮Z1=0的情況,此時式(19)可簡化為:

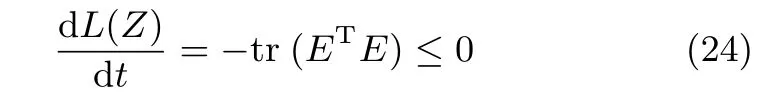
其中,E= Λ2Z2(ZT2Λ2Z2)?1?Z2A(ZT2Z2A)?2.

從式(24)可得:當且僅當E=0時,有dL(Z)/dt=0成立.此時,即.從式(23)和式(24)可得:對于任意的W∈??均有d(L(Z))/dt<0成立.因此,在域?內平穩點是漸近穩定的,即只要初始化狀態矩陣W在域?以內,則算法(13)全局漸近收斂到自相關矩陣矩陣R的前r個次成分.

4 仿真實驗

本節將通過兩個數值仿真實驗來驗證所提算法的性能.第一個實驗是考察所提算法提取多維次成分的能力,第二個實驗將所提算法與一些現有算法進行對比.在仿真實驗過程中,為了衡量算法的性能,這里采取兩個評價函數,第一個是方向余弦(Direction cosine,DC):

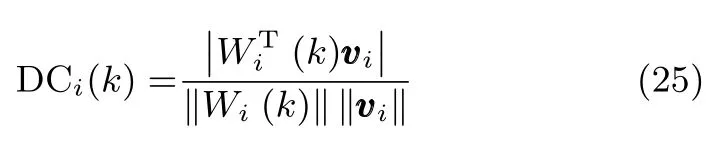
其中,Wi(k)表示在k時刻神經網絡狀態矩陣的第i列,而vi則是代表著自相關矩陣R的第i個次成分.顯然,如果Wi(k)能夠收斂到次成分vi的方向,則方向余弦的值應該收斂到1.

方向余弦只能評價狀態矩陣的收斂方向,而狀態矩陣模值也是一個非常重要的評價函數:

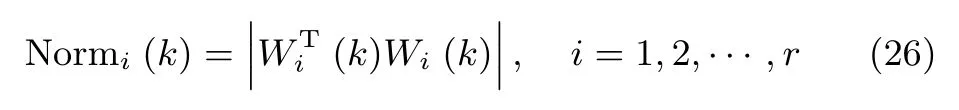
當神經網絡狀態矩陣收斂到次成分的方向(此時方向余弦等于1)時,如果狀態矩陣模值能夠收斂到一個常值,則算法是收斂的.

4.1 多維次成分提取實驗

本實驗考察所提算法提取多維次成分的能力.實驗中,輸入信號由式x(k)=T z(k)產生,其中,T=randn(10,10)/10是一個隨機產生的10×10維矩陣,而z(k)∈R10×1是一個均值為零方差為σ2=1的高斯白噪聲序列.這里分別采用WOJAm算法和RLS-WOJAm算法對信號的前3個次成分進行提取(即r=3).兩種算法的初始化參數設置如下:根據加權矩陣ar>ar?1>···>a1>0的要求,這里取加權矩陣A=diag{3,2,1};根據0<η≤1要求,同時也要保證算法的收斂性能,這里取學習因子η=0.1;由于輸入信號是一個近似平穩的隨機過程,所以這里取遺忘因子α=0.998;此外RLS-WOJAm算法中初始化逆矩陣P(0)=0.001×I3,其中I3是一個3×3的單位矩陣.兩個算法的采取相同的初始化狀態矩陣,且該矩陣是隨機產生的.仿真結果如圖1～圖4所示,該結果是100次獨立實驗的平均值.

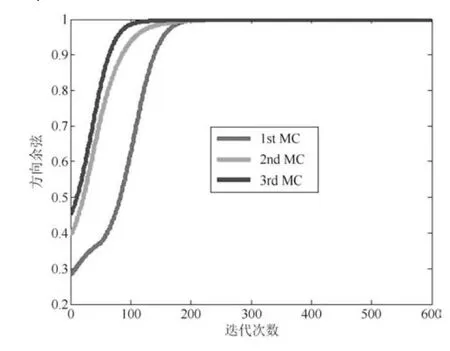
圖1 WOJAm算法的DC曲線Fig.1DC curves of WOJAm algorithm

圖1和圖3分別是兩種算法狀態矩陣列向量與所求次成分之間的方向余弦曲線;圖2和圖4分別是狀態矩陣各列向量的模值,黑線則是整個狀態矩陣的F-范數.從圖1和圖3中可以看出,經歷若干次迭代后,WOJAm算法和RLS-WOJAm算法的方向余弦均收斂到1,即兩種算法均最終收斂到了信號次成分的方向.從圖2和圖3中可得:兩種算法在方向余弦收斂到1的同時,狀態矩陣模值也已經收到一個常值.綜合兩圖可以得出結論:本文所提兩種算法均能夠自適應地提取信號的多維次成分,而且具有很好的收斂特性.

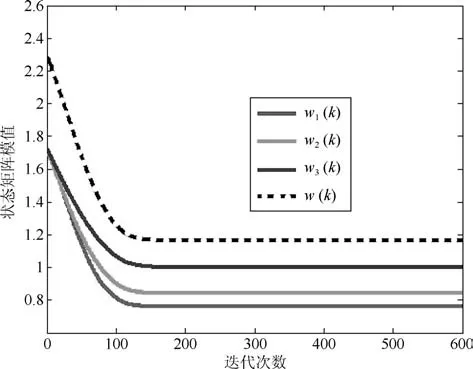
圖2 WOJAm算法的Norm曲線Fig.2 Norm curves of WOJAm algorithm

此外對比上述4圖可以得出結論:對于方向余弦曲線和狀態矩陣模值曲線,WOJAm算法和RLS-WOJAm算法的收斂情況近似相同,只是WOJAm算法的收斂速度略快于RLS-WOJAm算法.由于RLS-WOJAm算法是由WOJAm算法推導而來,兩者本質上是相同的,所以上述現象很容易解釋.從第2.3節可得,RLS-WOJAm算法的計算復雜度遠小于WOJAm算法,因此RLS-WOJAm算法更符合實際使用需要.在后續實驗中,將重點對RLS-WOJAm算法的性能進行考核.

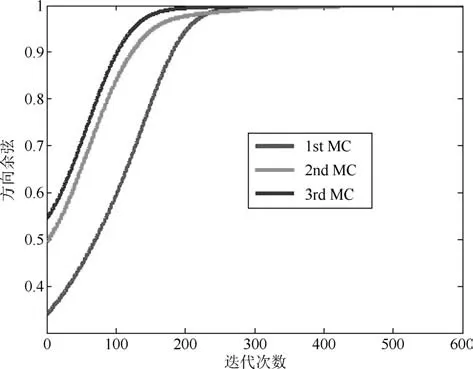
圖3 RLS-WOJAm算法的DC曲線Fig.3 DC curves of RLS-WOJAm algorithm

4.2 算法性能對比實驗

為了突出所提算法的性能,本實驗將所提RLS-WOJAm算法與MCA-OOJAH算法[12]和AMMD算法[11]進行比較.實驗中輸入信號采用如下一階滑動回歸模型來產生:

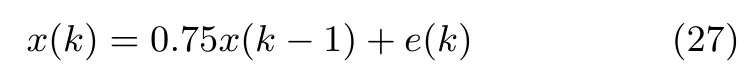
該模型由一個均值為零方差為1的高斯白噪聲e(k)作為模型驅動輸入.取該模型的10個不連續的輸出構成神經網絡的輸入向量.然后利用上述三種算法對該輸入信號的前3個次成分進行提取,即r=3.試驗中三個算法采用相同的初始化狀態矩陣,學習因子也都設置為0.1,仿真結果如圖5～圖8所示.

圖5～圖7分別是所提次成分的方向余弦曲線,圖8是在迭代過程中三種算法的狀態矩陣模值曲線.從圖8中可以看出,由于MCA-OOJAH算法在迭代過程中存在模值歸一化操作,所以其模值始終為一常值,而RLS-WOJAm算法和AMMD算法雖然沒有歸一化操作,但狀態矩陣模值仍能收斂到一個固定值.從圖5～圖7中可以發現:在所有次成分的提取過程中,RLS-WOJAm算法的收斂速度均快于其他兩種算法.

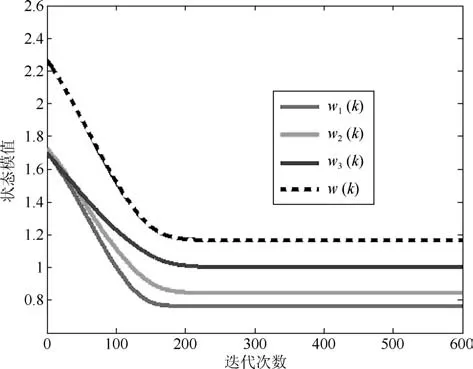
圖4 RLS-WOJAm算法的Norm曲線Fig.4 Norm curves of RLS-WOJAm algorithm

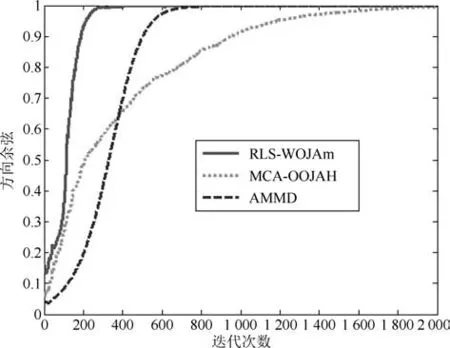
圖5 第一個次成分的DC曲線Fig.5 DC curves of the 1st MC

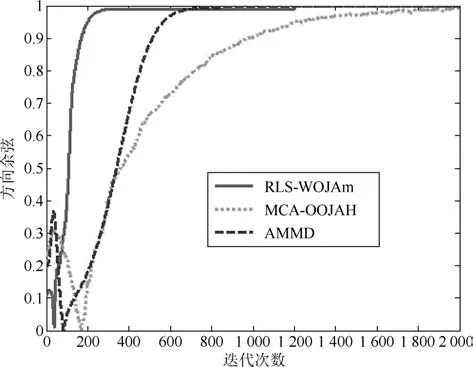
圖6 第二個次成分的DC曲線Fig.6 DC curves of the 2nd MC

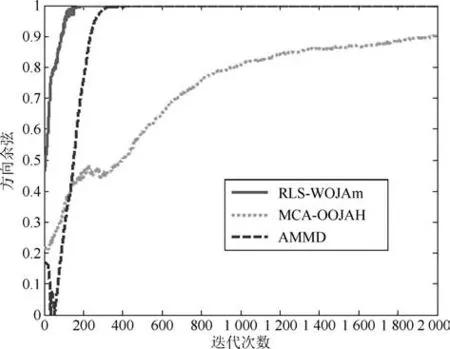
圖7 第三個次成分的DC曲線Fig.7 DC curves of the 3rd MC

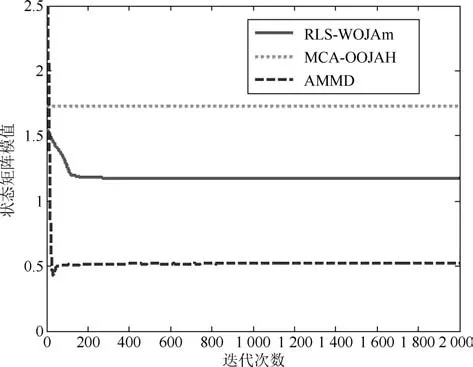
圖8 三種算法的Norm曲線Fig.8 Norm curves of the three algorithms

5 結論

本文對多維次成分并行提取算法進行了研究.首先,通過對OJAm次子空間跟蹤算法進行加權改造,提出了一種多維次成分并行提取算法;然后,為了降低該的計算復雜度的,采用遞歸最小二乘技術導出了一種新型算法—RLS-WOJAm算法;相比現有算法,所提算法對信號自相關矩陣的特征值大小沒有要求,也沒有模值歸一化措施;最后,通過李雅普諾夫函數法確定了所提算法的全局收斂域.仿真實驗表明:相比現有一些同類型算法,所提算法具有較快的收斂速度.