一種新的基于橢圓曲線碼的子域子碼的McEliece密碼系統(tǒng)
趙鴻伯 錢路雁 金玲飛,2
1(復(fù)旦大學(xué)計算機科學(xué)技術(shù)學(xué)院 上海 201203) 2(東南大學(xué)移動通信國家重點實驗室 江蘇 南京 210096)
0 引 言
1994年,Shor提出了能夠在多項式時間復(fù)雜度內(nèi)解決整數(shù)分解問題和離散對數(shù)問題的量子算法[1],這意味著在可實用的量子計算機出現(xiàn)的背景下,現(xiàn)今被廣泛使用的RSA公鑰密碼系統(tǒng)及橢圓曲線公鑰密碼系統(tǒng)將不再安全。因此,密碼學(xué)界開始研究能夠抵抗量子計算機攻擊的后量子密碼系統(tǒng),基于編碼理論的密碼系統(tǒng)便是后量子密碼系統(tǒng)中的一類。
第一個基于編碼理論的密碼系統(tǒng)是由McEliece在1978年提出的基于二元Goppa碼的McEliece公鑰密碼系統(tǒng)[2]。這一密碼系統(tǒng)與現(xiàn)今使用的公鑰密碼系統(tǒng)相比擁有更快的加解密速度。到目前為止,尚沒有有效的針對基于Goppa碼的密碼系統(tǒng)的攻擊方法。
在后續(xù)的研究中,學(xué)者們嘗試使用其他的糾錯碼來構(gòu)造新的McEliece密碼系統(tǒng)。2005年,Gaborit提出使用QC-BCH碼來構(gòu)造新的McEliece密碼系統(tǒng)[3]。2007年,Baldi等[4]提出了基于QC-LDPC碼的McEliece密碼方案。2009年,Berger等[5]介紹了使用QC-alternant碼構(gòu)造的McEliece密碼方案。2013年,Misoczki等[6]構(gòu)造了基于QC-MDPC碼的McEliece密碼系統(tǒng)。2018年,NIST舉行的后量子密碼學(xué)標(biāo)準(zhǔn)競賽上,多個基于編碼理論的密碼系統(tǒng)進入第一輪競爭,Aragon等[7]提出了基于QC-MDPC碼的BIKE密碼系統(tǒng),Melchor等[8]學(xué)者提出的基于QC碼的HQC密碼系統(tǒng)等。
上述的部分密碼方案被證明存在弱點。2010年,Otmani等[9]提出了針對Gaborit和Baldi提出的基于QC-BCH碼和QC-LDPC碼的McEliece密碼系統(tǒng)的攻擊方法。同一年,F(xiàn)augère等[10]提出了針對Berger等人設(shè)計的基于QC-alternant碼的McEliece密碼方案的攻擊方法。2016年,Guo等[11]提出了針對Misoczki等人構(gòu)造的基于QC-MDPC碼的McEliece密碼方案的攻擊方法。
除了上述方案外,1996年,Janwa和Moreno提出代數(shù)幾何碼及其子碼可以作為構(gòu)造McEliece密碼系統(tǒng)的一種選擇[12]。雖然基于代數(shù)幾何碼及其子碼的McEliece密碼系統(tǒng)已經(jīng)被證明不安全[13]。但目前尚沒有針對基于代數(shù)幾何碼的子域子碼的McEliece密碼系統(tǒng)的有效的攻擊方法,代數(shù)幾何碼的子域子碼仍然可以作為構(gòu)造McEliece公鑰密碼方案的一個選擇。
本文的主要貢獻在于構(gòu)造了一個新的基于橢圓曲線碼的子域子碼的McEliece公鑰密碼系統(tǒng)。
1 預(yù)備知識
1.1 線性碼基礎(chǔ)知識
1.2 代數(shù)幾何碼
Goppa于1977年發(fā)現(xiàn)了編碼理論與代數(shù)幾何之間的理論聯(lián)系,并在1981年提出了代數(shù)幾何碼的構(gòu)造方法[14]。

(1)
這個賦值映射的像就是一個從曲線X上構(gòu)造的代數(shù)幾何碼,記為CL(X,P,E)。CL(X,P,E)的碼長n等于有理點的個數(shù),即n=|P|。CL(X,P,E)維數(shù)k等于L(E)的維數(shù),即k=dim(L(E))。CL(X,P,E)的碼距d由曲線X的虧格g決定,滿足條件n-k-g+1≤d≤n-k+1[16]。
1989年,Justesen等學(xué)者提出了構(gòu)造基于有限域上的光滑不可約仿射曲線的代數(shù)幾何碼的簡易方法[17]。根據(jù)單項式基底F(x)和曲線的一個有理點集P,可以構(gòu)造出曲線上的代數(shù)幾何碼的生成矩陣:
(2)
1.3 McEliece密碼系統(tǒng)
初始的McEliece密碼系統(tǒng)是基于Goppa碼構(gòu)建的。該密碼系統(tǒng)由密鑰生成、加密算法和解密算法三個部分構(gòu)成。
1.3.1 密鑰生成
1) 在有限域F2m上隨機選取一個度數(shù)為t的不可約多項式。根據(jù)這一多項式構(gòu)造一個參數(shù)[n,k,d]Goppa碼的生成矩陣G,其中n=2m,d=2t+1。
2) 隨機選擇一個k×k的可逆矩陣S和一個n×n的置換矩陣P。
3) 計算公鑰Gpub=SGP。
4) 將集合(S,φ,P)作為私鑰保存,其中φ代表二元Goppa碼的快速譯碼算法。
1.3.2 加密算法
令m代表一個長度為k的消息向量。加密算法的執(zhí)行過程如下:
1) 隨機生成一個長度為n的錯誤向量e,滿足wt(e)≤t。
2) 計算密文c=mGpub+e。
1.3.3 解密算法
對于獲得的密文c,解密算法的執(zhí)行過程如下:
1) 消除置換矩陣的影響:計算x=cP-1=mSG+eP-1。
2) 使用譯碼算法φ清除錯誤向量:u=φ(x)。
3) 計算消息向量:m=uS-1。
2 基于橢圓曲線碼的子域子碼的McEliece公鑰密碼系統(tǒng)
2.1 基本思路
與其他代數(shù)幾何碼的子域子碼相比,橢圓曲線碼的子域子碼擁有更長的碼距。同時,2.4節(jié)中介紹了針對橢圓曲線碼的子域子碼的快速譯碼算法。這使得橢圓曲線碼的子域子碼成為構(gòu)造McEliece公鑰密碼系統(tǒng)的一個選擇。
本節(jié)將介紹基于橢圓曲線碼的子域子碼的McEliece公鑰密碼系統(tǒng)。與初始的McEliece公鑰密碼系統(tǒng)類似,基于橢圓曲線碼的子域子碼的McEliece公鑰密碼系統(tǒng)也由密鑰生成、加密算法和解密算法三個部分組成。
2.2 密鑰生成
2.2.1 構(gòu)造橢圓曲線碼
2) 隨機選擇X上的n個有理點P(α,β)構(gòu)成有理點集P={P1,P2,…,Pn}。
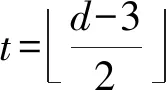
4) 將F(x,y)按照V(f1)≤V(f2)≤…≤V(fn-t-1)順序排列,其中V(f)=2i+3j。
5) 使用F(x,y)的前k個單項式Fk(x,y)和有理點集P構(gòu)造橢圓曲線碼的生成矩陣Ge。構(gòu)造的橢圓曲線碼的參數(shù)為[n,k,d],其中d=n-k。
2.2.2 構(gòu)造橢圓曲線碼的子域子碼
1) 根據(jù)Ge計算橢圓曲線碼的校驗矩陣He。
3) 橢圓曲線碼的子域子碼的生成矩陣G是H2的零空間的一個基底。構(gòu)造的子域子碼的參數(shù)為[N,K,D],其中N=n,K≥mk-(m-1)n,D≥d。
2.2.3 生成密鑰
1) 隨機挑選一個F2上的k×k可逆矩陣S,一個n×n轉(zhuǎn)置矩陣P。
2) 計算公鑰Gpub=SGP。
3) 將有理點集P,可逆矩陣S和轉(zhuǎn)置矩陣P作為私鑰保存。
2.3 加密算法
對一個消息向量m的加密過程如下:
1) 隨機生成一個長度為n的錯誤向量e且wt(e)≤t。
2) 生成密文r=mGpub+e。
2.4 解密算法
2.4.1 橢圓曲線碼的子域子碼的快速譯碼算法
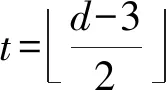
1) 構(gòu)造兩個多項式A(x,y)、B(x,y):
A(x,y)=a1f1+a2f2+…+an-t-1fn-t-1
(3)
B(x,y)=b1f1+b2f2+…+bn-t-k-1fn-t-k-1
(4)
其中,ai,bi∈q,fi∈F(x,y)。
2) 構(gòu)造方程組A(Pi)+B(Pi)f(Pi)=0,找到A、B的一個非零解:
(5)
4) 糾錯后的碼字為{d(P1),d(P2),…,d(PPn)}。
2.4.2 快速譯碼算法證明
本節(jié)將證明橢圓曲線碼的子域子碼的快速譯碼算法的正確性。
1) 證明多項式A(x,y)、B(x,y)的存在性:將ai、bj看作是未知數(shù),則式(5)是一個包含n個齊次線性方程的齊次方程組。其中未知數(shù)的個數(shù)為2(n-t-1)-k 2) 證明糾錯后的碼字等于{d(P1),d(P2),…,d(Pn)}。不妨設(shè)收到的碼字mGpub等于(f(P1),f(P2),…,f(Pn)),其中V(f)≤k。由1)知,至少有n-t個有理點Pi使得A(Pi)+B(Pi)f(Pi)=0。又由V(A+Bf) 2.4.3 解密算法 根據(jù)上文介紹的橢圓曲線碼的子域子碼的快速譯碼算法,對收到的密文r=mSGP+e={r1,r2,…,rn},解密算法過程如下: 1) 消除置換矩陣P的影響:r′=rP-1=mSG+e′。 2) 清除錯誤位:m′=Φ(r′)=mS。 3) 恢復(fù)消息向量:m=m′S-1。 目前,針對McEliece密碼系統(tǒng)主要存在兩類攻擊方法。第一類攻擊嘗試從密文中恢復(fù)明文信息的信息恢復(fù)攻擊,信息集譯碼攻擊算法是這一類攻擊算法的代表,3.2節(jié)中討論了信息集譯碼攻擊算法對提出的密碼方案的安全性的影響。第二類是根據(jù)選取的編碼的性質(zhì),試圖從公鑰中恢復(fù)私鑰的密鑰恢復(fù)攻擊。目前,尚沒有直接針對基于橢圓曲線碼的子域子碼的McEliece密碼系統(tǒng)的密鑰恢復(fù)攻擊方法。由于橢圓曲線碼是構(gòu)建在虧格為1的代數(shù)曲線上的代數(shù)幾何碼,因此3.4節(jié)中討論了針對基于代數(shù)幾何碼的McEliece密碼系統(tǒng)的密鑰恢復(fù)攻擊對提出的密碼系統(tǒng)的影響。最終證明,在現(xiàn)有的攻擊方法下,本文中提出的密碼系統(tǒng)是安全的。 窮搜攻擊的基本思路是根據(jù)公鑰矩陣的信息,通過遍歷搜索所有可能的k×k可逆矩陣,n×n置換矩陣以及使用的有理點集的方法,恢復(fù)出私鑰(S,P,P)。在2上,k×k可逆矩陣的個數(shù)為置換矩陣的個數(shù)為在q上,不同構(gòu)的橢圓曲線的個數(shù)約為|X|≈2q[19]。橢圓曲線上的有理點的數(shù)量區(qū)間為橢圓曲線上基數(shù)為n的有理點集|P|的數(shù)量區(qū)間為 基于上述分析,攻擊者成功實施窮搜攻擊的可能性為1/|S||P||P||X|。當(dāng)n、k取較大值時,設(shè)計的密碼系統(tǒng)能夠有效抵御窮搜攻擊。 1962年,Prange針對一般線性碼的譯碼問題提出了信息集譯碼算法[20]。 定義1令G代表一個[n,k]線性碼C的生成矩陣,I代表{1,2,…,n}的一個基數(shù)為k的子集。選擇G中以I為索引的列構(gòu)成一個k×k矩陣GI。若GI可逆,則稱I為G的一個信息集。 下面是信息集譯碼算法的一個簡單例子。 令I(lǐng)代表q上的一個線性碼C的生成矩陣G的一個信息集,y代表上的一個向量,c代表C的一個碼字,且d(y,c)=w,w≠0。令yI和cI代表按I索引的y和c的子集。若yI=cI,則可以計算碼字 表1 信息集譯碼攻擊算法的時間復(fù)雜度 1997年,Berson和Thomas證明McEliece公鑰密碼系統(tǒng)在消息重傳場景下是不安全的[26]。 令m代表一個明文向量。假設(shè)存在兩個由m生成的密文c1=mGpub+e1和c2=mGpub+e2其中e1≠e2。由McEliece密鑰方案的初始定義可知c1-c2=e1-e2。根據(jù)這一關(guān)系,攻擊者可以快速的找到一個信息集I使得cI=mI,從而恢復(fù)出明文m。 和初始的McEliece密鑰方案相同,基于橢圓曲線碼的子域子碼的McEliece密鑰方案在消息重傳場景下也是不安全的。 為了使McEliece密碼系統(tǒng)達到CCA-2安全級別。有學(xué)者提出了可用于基于編碼理論的密碼系統(tǒng)的具有CCA-2安全級別的加密方案[27-28]。 目前,尚沒有針對基于代數(shù)幾何碼的子域子碼的McEliece密碼系統(tǒng)的攻擊方法。由于選擇的編碼是代數(shù)幾何碼的一類子碼,本節(jié)將分析針對基于代數(shù)幾何碼的McEliece密鑰系統(tǒng)的攻擊方法對提出的密鑰系統(tǒng)的安全性能的影響。 3.4.1 Faure的攻擊算法 2007年,F(xiàn)aure和Minder提出了針對基于橢圓曲線碼的McEliece密鑰系統(tǒng)的攻擊算法[29]。這一算法的基本思路是,根據(jù)橢圓曲線上所有有理點構(gòu)成的阿貝爾群,攻擊者能夠找到一條與選擇的曲線同構(gòu)的橢圓曲線,并最終根據(jù)兩條曲線間的映射來恢復(fù)所選用的橢圓曲線。 為了從公開信息中構(gòu)造所選用的橢圓曲線的所有有理點構(gòu)成的阿貝爾群,攻擊者需要找到所選用的橢圓曲線碼的一個具有最小漢明重量的碼字。 定義2對于一個[n,k,d]橢圓曲線碼,其碼字的最小漢明重量等于它的碼距d=n-k。 橢圓曲線碼的子域子碼的碼距大于等于其原碼的碼距。在實際構(gòu)造中,當(dāng)橢圓曲線碼所在的有限域大于26時,總能構(gòu)造出碼距大于原碼碼距的子域子碼。比如,參數(shù)為[64,54,10]的橢圓曲線碼的子域子碼的參數(shù)為[64,10,16],參數(shù)為[128,113,15]的橢圓曲線碼的子域子碼的參數(shù)為[128,23,36]。 無法從子域子碼中獲得原碼的一個具有最小漢明重量的碼字使得Faure的攻擊算法對提出的密碼方案無效。 3.4.2 Couvreur的攻擊算法 2017年,Couvreur等人提出了針對基于代數(shù)幾何碼及其子碼的McEliece系統(tǒng)的攻擊算法。但Couvreur等在論文中闡明,這一攻擊算法并不適用于基于代數(shù)幾何碼的子域子碼的McEliece密碼系統(tǒng)[13]。 與最初的McEliece密碼方案相同。提出的基于橢圓曲線碼的子域子碼的McEliece密碼系統(tǒng)的公鑰是一個大小為n×k比特的矩陣。合適的具有CCA-2安全級別的加密方案能夠在保持安全性能的同時,將密鑰方案的公鑰轉(zhuǎn)變?yōu)橐粋€大小為(n-k)×k比特的標(biāo)準(zhǔn)形式矩陣[30]。 本文的主要貢獻在于構(gòu)造了一個新的基于橢圓曲線碼的子域子碼的McEliece公鑰密碼系統(tǒng)。并使用針對McEliece公鑰密碼系統(tǒng)的攻擊算法及針對基于代數(shù)幾何碼的McEliece密碼系統(tǒng)的攻擊算法對提出系統(tǒng)的安全性能進行分析。分析證明,在現(xiàn)有的攻擊下,本文提出的基于橢圓曲線碼的子域子碼的公鑰密碼系統(tǒng)是安全的。 未來該方案可作為基于編碼理論的密碼系統(tǒng)的一個備選方案,在數(shù)字簽名、零知識證明等方面展開進一步的研究。3 安全性能分析
3.1 窮搜攻擊
3.2 信息集譯碼攻擊
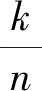

3.3 消息重傳攻擊
3.4 針對基于代數(shù)幾何碼的McEliece公鑰系統(tǒng)的密鑰恢復(fù)攻擊
3.5 公鑰體積及推薦參數(shù)
4 結(jié) 語

