夯實基礎,學好直線
伏建彬
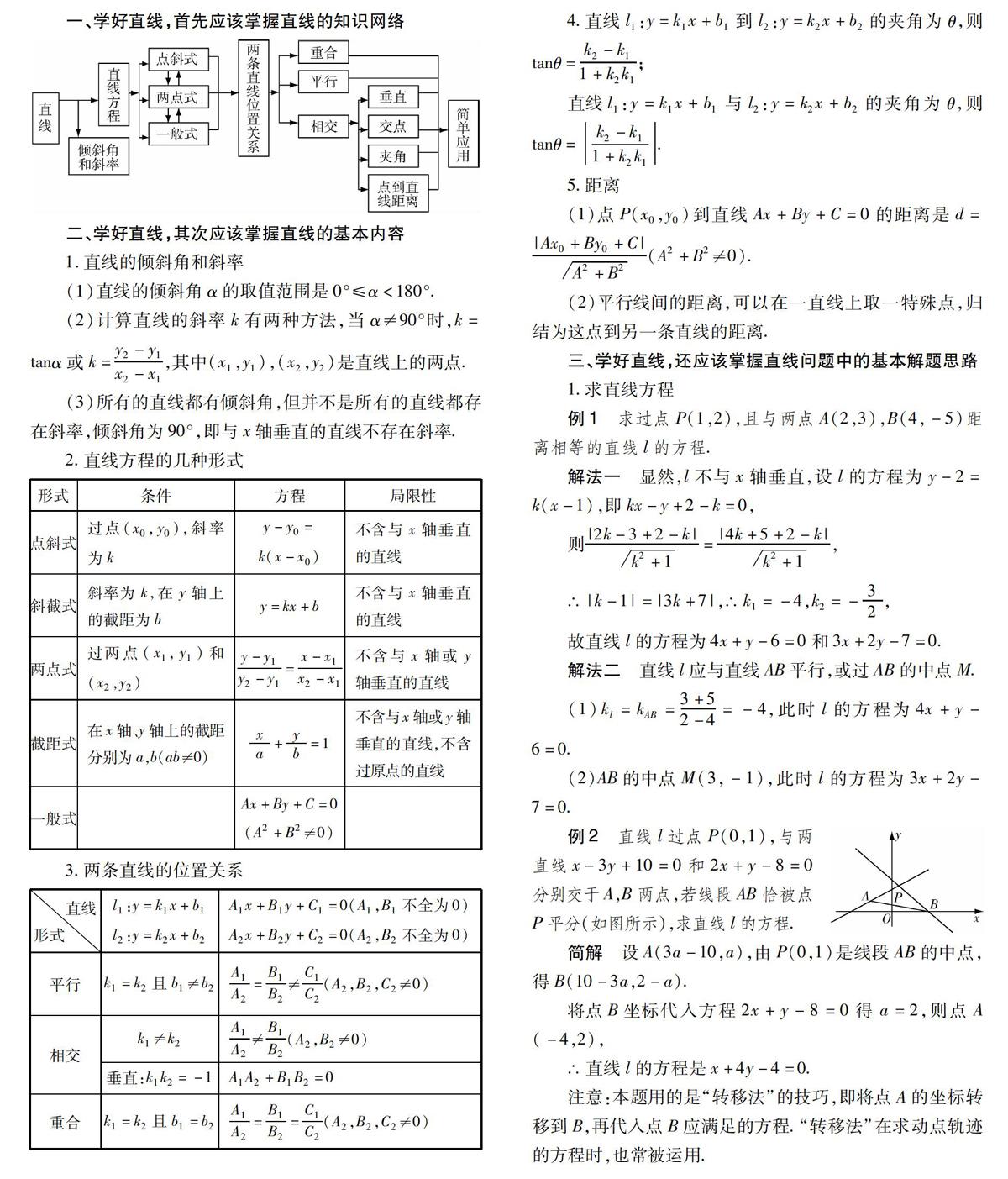
一、學好直線,首先應該掌握直線的知識網絡
二、學好直線,其次應該掌握直線的基本內容
1.直線的傾斜角和斜率
(1)直線的傾斜角α的取值范圍是0°≤α<180°.
(2)計算直線的斜率k有兩種方法,當α≠90°時,k=tanα或k= y2-y1 x2-x1 ,其中(x1,y1),(x2,y2)是直線上的兩點.
(3)所有的直線都有傾斜角,但并不是所有的直線都存在斜率,傾斜角為90°,即與x軸垂直的直線不存在斜率.
2.直線方程的幾種形式
形式? 條件 方程? 局限性
點斜式 過點(x0,y0),斜率為k y-y0=k(x-x0) 不含與x軸垂直的直線
斜截式 斜率為k,在y軸上的截距為b y=kx+b 不含與x軸垂直的直線
兩點式 過兩點(x1,y1)和(x2,y2)? y-y1 y2-y1 = x-x1 x2-x1? 不含與x軸或y軸垂直的直線
截距式? 在x軸、y軸上的截距分別為a,b(ab≠0)?? x a + y b =1? 不含與x軸或y軸垂直的直線,不含過原點的直線
一般式? Ax+By+C=0(A2+B2≠0)
3.兩條直線的位置關系
直線形式?? l1:y=k1x+b1l2:y=k2x+b2
A1x+B1y+C1=0(A1,B1不全為0)
A2x+B2y+C2=0(A2,B2不全為0)
平行 k1=k2且b1≠b2? A1 A2 = B1 B2 ≠ C1 C2 (A2,B2,C2≠0)
相交
k1≠k2? A1 A2 ≠ B1 B2 (A2,B2≠0)
垂直:k1k2=-1 A1A2+B1B2=0
重合 k1=k2且b1=b2? A1 A2 = B1 B2 = C1 C2 (A2,B2,C2≠0)
4.直線l1:y=k1x+b1到l2:y=k2x+b2的夾角為θ,則tanθ= k2-k1 1+k2k1 ;
直線l1:y=k1x+b1與l2:y=k2x+b2的夾角為θ,則tanθ=? k2-k1 1+k2k1? .
5.距離
(1)點P(x0,y0)到直線Ax+By+C=0的距離是d= |Ax0+By0+C|? A2+B2? (A2+B2≠0).
(2)平行線間的距離,可以在一直線上取一特殊點,歸結為這點到另一條直線的距離.
三、學好直線,還應該掌握直線問題中的基本解題思路
1.求直線方程
例1?? 求過點P(1,2),且與兩點A(2,3),B(4,-5)距離相等的直線l的方程.
解法一? 顯然,l不與x軸垂直,設l的方程為y-2=k(x-1),即kx-y+2-k=0,
則 |2k-3+2-k|? k2+1? = |4k+5+2-k|? k2+1? ,
∴|k-1|=|3k+7|,∴k1=-4,k2=- 3 2 ,
故直線l的方程為4x+y-6=0和3x+2y-7=0.
解法二? 直線l應與直線AB平行,或過AB的中點M.
(1)kl=kAB= 3+5 2-4 =-4,此時l的方程為4x+y-6=0.
(2)AB的中點M(3,-1),此時l的方程為3x+2y-7=0.
例2?? 直線l過點P(0,1),與兩直線x-3y+10=0和2x+y-8=0 分別交于A,B兩點,若線段AB恰被點P平分(如圖所示),求直線l的方程.
簡解? 設A(3a-10,a),由P(0,1)是線段AB的中點,得B(10-3a,2-a).
將點B坐標代入方程2x+y-8=0得a=2,則點A(-4,2),
∴直線l的方程是x+4y-4=0.
注意:本題用的是“轉移法”的技巧,即將點A的坐標轉移到B,再代入點B應滿足的方程.“轉移法”在求動點軌跡的方程時,也常被運用.

