不同圍壓和振幅下巖石循環(huán)荷載動(dòng)力特征分析

，，，，，

(1.地質(zhì)災(zāi)害防治與地質(zhì)環(huán)境保護(hù)國家重點(diǎn)實(shí)驗(yàn)室(成都理工大學(xué))，四川成都610059；2.成都理工大學(xué)地質(zhì)工程國家級(jí)實(shí)驗(yàn)教學(xué)示范中心，四川成都610059；3.中國能源建設(shè)集團(tuán)廣東省電力設(shè)計(jì)研究院有限公司，廣東廣州510663)

巖體在工程中不僅要承受自然界穩(wěn)定的荷載，還要承受工程施工過程中的爆破，工程機(jī)械的往復(fù)運(yùn)動(dòng)和地震等的往復(fù)荷載。這些往復(fù)的荷載會(huì)影響巖石的強(qiáng)度和力學(xué)性質(zhì)，使得巖體的穩(wěn)定性大打折扣，導(dǎo)致工程和人民財(cái)產(chǎn)的損失。于是，對(duì)于循環(huán)荷載下的巖石應(yīng)力應(yīng)變和力學(xué)參數(shù)變化規(guī)律的研究有著重要的意義。

以往的研究表明，在循環(huán)荷載下，不同的因素會(huì)使得材料表現(xiàn)出不同的力學(xué)行為[1]。影響巖石的動(dòng)力特征的因素有很多，例如圍壓、試樣內(nèi)部的原生結(jié)構(gòu)、加載的應(yīng)力幅值、還有頻率等。Eyal Shalev等人[2]基于不同幅值砂巖的循環(huán)加載試驗(yàn)，分析了加卸載過程中的滯回效應(yīng)及幅值對(duì)體應(yīng)變、體積模量的影響；郭印同等人[3]研究發(fā)現(xiàn)提高循環(huán)荷載上限應(yīng)力和平均應(yīng)力的大小會(huì)顯著影響巖石疲勞破壞的過程；劉建鋒等人[4]通過不同頻率和幅值的循環(huán)荷載試驗(yàn)，得到了頻率和幅值對(duì)大理巖動(dòng)彈性模量和動(dòng)泊松比的影響規(guī)律；肖建清[5]、朱明理[6]、Nishi[7]、朱珍德[8]等學(xué)者通過循環(huán)荷載試驗(yàn)得到了巖石的阻尼參數(shù)，討論了阻尼特性。此外，Mckavanagh等人[9]考慮了低應(yīng)變阻尼和頻率下的巖石滯后性；鄧華鋒等對(duì)不同環(huán)境砂巖的強(qiáng)度影響以及巖石循環(huán)荷載的滯后性和巖石抗壓強(qiáng)度的預(yù)測(cè)進(jìn)行了研究[10-12]，葛修潤等對(duì)周期荷載下巖石疲勞變形進(jìn)行了研究[13]，劉建鋒等對(duì)循環(huán)荷載下巖石阻尼進(jìn)行了研究[14]，Ladani L J[15]、張慧梅[16]、張世殊[17]等學(xué)者對(duì)巖石在循環(huán)荷載條件下的損傷進(jìn)行了研究；李成杰等[18]對(duì)砂巖進(jìn)行等荷載循環(huán)加卸載試驗(yàn)，探究了其變形滯回環(huán)特征；王金鵬等[19]對(duì)軟巖循環(huán)荷載下力學(xué)性能進(jìn)行了研究。

因此對(duì)于巖石循環(huán)的研究基本集中于巖石阻尼、變形、疲勞等方面，對(duì)于巖石在不同環(huán)境下的動(dòng)力學(xué)特征的研究工作還不是很充分，于是本文選用中等風(fēng)化砂巖試樣，進(jìn)行單軸、三軸的不同圍壓下的循環(huán)荷載試驗(yàn)，探討不同壓力、不同的應(yīng)力幅值對(duì)巖石動(dòng)力學(xué)特性的影響，分析阻尼比，動(dòng)彈性模量曲線形態(tài)特點(diǎn)，砂巖應(yīng)力～應(yīng)變滯回曲線的形態(tài)特征，應(yīng)力曲線和應(yīng)變曲線滯后性產(chǎn)生相位差與巖石損傷的關(guān)系。

1 巖石試樣選擇與試驗(yàn)方案設(shè)計(jì)

1.1 試樣選擇

本次試驗(yàn)的樣品為中等風(fēng)化砂巖，按照《水利水電工程巖石試驗(yàn)規(guī)程》制樣要求，將巖石制成直徑為(50±1) mm，高為(100±1) mm的圓柱標(biāo)準(zhǔn)樣。進(jìn)行波速測(cè)試之后，選取波速較為接近的試樣進(jìn)行試驗(yàn)。本次選取的試驗(yàn)樣品參數(shù)見表1。

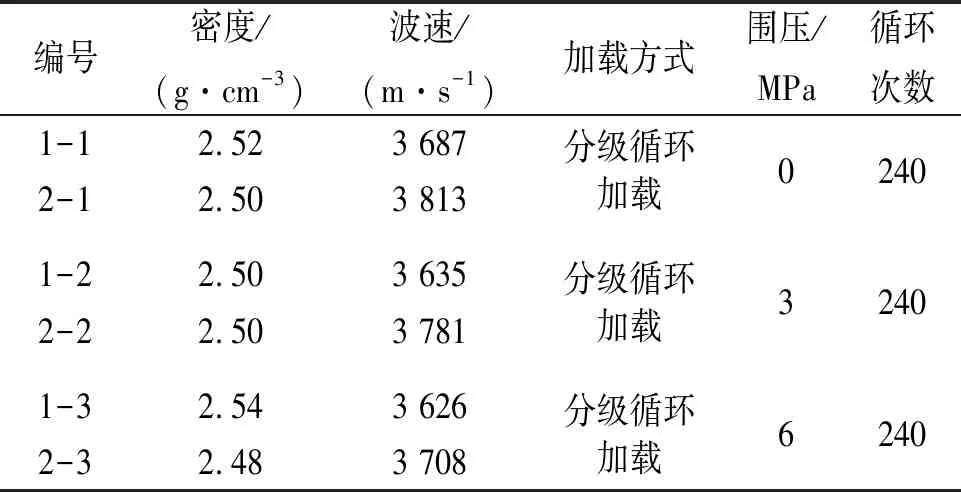
表1 試樣參數(shù)

本次試驗(yàn)方案先對(duì)巖樣進(jìn)行單軸、三軸常規(guī)靜力試驗(yàn)，求出其單軸抗壓強(qiáng)度為21.4 MPa左右，圍壓3 MPa時(shí)的抗壓強(qiáng)度為40.2 MPa左右，圍壓為6 MPa時(shí)的抗壓強(qiáng)度為45.2 MPa左右，在此基礎(chǔ)上，分組開展巖石動(dòng)力試驗(yàn)，總共6個(gè)試樣，其中圍壓為0 MPa的試驗(yàn)2個(gè)，圍壓為3 MPa的動(dòng)三軸試驗(yàn)2個(gè)，圍壓為6 MPa的動(dòng)三軸試驗(yàn)2個(gè)。

1.2 試驗(yàn)機(jī)器

本次試驗(yàn)設(shè)備為美國進(jìn)口的MTS巖石高溫高壓三軸試驗(yàn)機(jī)，見圖1。該試驗(yàn)機(jī)進(jìn)行的振動(dòng)試驗(yàn)，振動(dòng)頻率達(dá)3 Hz以上，振動(dòng)波形可為正弦波、三角波、方波、斜波及隨機(jī)波，振動(dòng)相位差可在0～2π任意設(shè)定，具有多種控制模式，并可在試驗(yàn)過程中進(jìn)行多種控制模式間的任意轉(zhuǎn)換，是先進(jìn)的室內(nèi)巖石力學(xué)試驗(yàn)設(shè)備。

1.3 試驗(yàn)循環(huán)荷載加載方法

每個(gè)試樣均采用分級(jí)動(dòng)荷載加載試驗(yàn)，波形為正弦波，每一級(jí)振動(dòng)頻率為1 Hz，循環(huán)次數(shù)為30次，循環(huán)荷載下限為1 MPa，上限為常規(guī)三軸、單軸試驗(yàn)的強(qiáng)度的10%、20%、30%、40%、50%、60%、70%、80%，每級(jí)荷載增加10%，共8次。試驗(yàn)過程記錄動(dòng)單軸、三軸環(huán)境中試樣的相關(guān)物理、力學(xué)參數(shù)。

1.4 試驗(yàn)原理

由于巖石為非理想彈性體，其動(dòng)應(yīng)力與動(dòng)應(yīng)變的波形線在時(shí)間上并不完全對(duì)應(yīng)，兩者之間有一定的時(shí)間差，在動(dòng)應(yīng)力～動(dòng)應(yīng)變曲線上表現(xiàn)為卸載段曲線不沿原加載段曲線返回，卸載段低于加載段，于是會(huì)出現(xiàn)滯回環(huán)現(xiàn)象，見圖2。

如圖，滯回環(huán)ABC的面積的大小反映了巖石在循環(huán)加、卸載過程中能量損失的大小，滯回環(huán)的平均斜率反映了動(dòng)彈性模量Ed的大小，4倍的三角形AOD的面積反映了一個(gè)循環(huán)中所儲(chǔ)存的彈性應(yīng)變能。文中動(dòng)彈性模量和阻尼比的公式為:

(1)

(2)

(3)

式中σdmax——一次循環(huán)荷載中巖樣所受到的最大的應(yīng)力；σdmin——一次循環(huán)荷載中巖樣所受到的最小的應(yīng)力；εd1——每次循環(huán)荷載開始時(shí)試樣的軸向應(yīng)變量；εd2——每次循環(huán)荷載結(jié)束時(shí)試樣的軸向應(yīng)變量；εdm——εd1和εd2的中間應(yīng)變；εdmax——每次循環(huán)荷載加到最大值時(shí)試樣的軸向最大應(yīng)變量；AL——滯回環(huán)ABC的面積；AT——三角形AOD的面積。

2 不同圍壓條件下循環(huán)荷載應(yīng)力～應(yīng)變曲線分析

本次試驗(yàn)將圍壓分為0、3、6 MPa的3組進(jìn)行，其試樣應(yīng)力～應(yīng)變滯回環(huán)見圖3—5。由于巖石的應(yīng)變量很小，在同一個(gè)荷載振幅情況下，滯回環(huán)會(huì)擠在一起不好分辨，于是取每一個(gè)荷載幅值中第15次的滯回環(huán)進(jìn)行分析。

由上圖可以看到，在振動(dòng)荷載逐漸加大的同時(shí)，試樣的軸向永久塑性變形也在不斷增大，并且隨著荷載的增加，試樣的彈性變形也在不斷增加。在整體的滯回曲線中，表現(xiàn)為滯回曲線面積隨振動(dòng)荷載的增加而增加，這一現(xiàn)象表明試件振動(dòng)一個(gè)周期所消耗的能量的增長。其原因是隨著巖石的循環(huán)次數(shù)的上升，其內(nèi)部會(huì)出現(xiàn)細(xì)小的裂紋，在試樣循環(huán)加荷載的過程中，內(nèi)部的裂紋會(huì)隨著循環(huán)而發(fā)生周期性的張開、閉合，之后裂紋進(jìn)一步的擴(kuò)展，在宏觀上表現(xiàn)出能量消耗的增加，此現(xiàn)象也表明了試樣的損傷隨著循環(huán)的進(jìn)行而不斷加深。

在圍壓為0 MPa時(shí)試樣的滯回曲線發(fā)生了很大程度的內(nèi)凹，并且在前三級(jí)循環(huán)過程中，試樣的軸向應(yīng)變呈跳躍式的發(fā)展，隨著循環(huán)過程進(jìn)入第四級(jí)之后而逐漸趨于穩(wěn)定，當(dāng)圍壓從0 MPa增加到3 MPa和6 MPa時(shí)，滯回曲線由內(nèi)凹的尖葉形轉(zhuǎn)變?yōu)檩^為飽滿的橢圓形再轉(zhuǎn)變?yōu)楸容^上凸的尖葉形，說明圍壓對(duì)于滯回環(huán)的形態(tài)特征有一定的影響，并且隨著圍壓的增大，其軸向的應(yīng)變也在不斷的減少，說明圍壓對(duì)試樣有壓縮，緊固的作用，限制了其變形。在加大軸向荷載的同時(shí)，其各個(gè)滯回環(huán)的面積也在逐漸增大，說明能量的消耗在不斷增加，試樣的內(nèi)部破壞程度不斷增大，最后導(dǎo)致試樣破壞。

3 軸向應(yīng)變規(guī)律

取每一個(gè)滯回環(huán)的峰谷應(yīng)變?chǔ)興2作為計(jì)算的應(yīng)變，該應(yīng)變可以看作試樣的塑性應(yīng)變，做出應(yīng)變和振動(dòng)次數(shù)關(guān)系曲線見圖6，該曲線清晰地描繪了不同圍壓和不同軸向荷載狀況下，試樣的應(yīng)變發(fā)展。

該曲線總體上呈階梯形態(tài)分布，可以分為初始階段、穩(wěn)定階段和加速階段3個(gè)階段，應(yīng)變隨著振動(dòng)次數(shù)的增加而增加，在每30次的軸向荷載改變時(shí)，試樣內(nèi)部的微裂隙和組成晶體排列受到力的作用而壓密和重排列，從而使得試樣應(yīng)變有一個(gè)突然性的增加，這一階段為初始階段，之后隨著振動(dòng)而趨于平緩，為穩(wěn)定階段；通過輔助線(圖中虛線)可以看出，在試驗(yàn)的中后期，輔助線在相同振動(dòng)次數(shù)位置產(chǎn)生一個(gè)折點(diǎn)，在折點(diǎn)之后，輔助線的斜率增加說明整體應(yīng)變曲線斜率在不斷的增大，呈上翹的趨勢(shì)，這一階段為加速階段；以試樣2-3為例，從初始階段和穩(wěn)定階段到加速階段，輔助線的斜率從一開始的1.39×10-3變?yōu)?.08×10-3具體增長了約50%，此現(xiàn)象說明試樣在試驗(yàn)中后期，內(nèi)部的損傷不斷的發(fā)展和擴(kuò)大使得其塑性變形增長速率不斷增大。試樣應(yīng)變的大小隨著圍壓的增加而不斷降低，說明圍壓對(duì)試樣的應(yīng)變有抑制作用，圍壓越大，抑制作用越明顯。

4 動(dòng)彈性模量分析

不同圍壓下的不同循環(huán)荷載的每一個(gè)滯回曲線的動(dòng)彈性模量計(jì)算結(jié)果見圖7。由于本次試驗(yàn)的方案是每振動(dòng)30次保持最低軸向荷載不變，增加最高軸向荷載10 %，圖7也可以展示不同振幅與動(dòng)彈性模量Ed的關(guān)系。

可見，在試驗(yàn)前30次振動(dòng)中，每一組試樣的動(dòng)彈性模量都會(huì)有較大幅度的變化，其原因是試樣內(nèi)部有較大的孔隙和裂紋，組成巖石的礦物晶體的排列還不是很緊密，隨著軸向循環(huán)荷載的施加，試樣內(nèi)部的孔隙和晶體隨著循環(huán)呈周期性的壓密和回彈而不斷重新壓密和破裂，從而導(dǎo)致其彈性模量的變化幅度較大。在振幅保持不變的循環(huán)過程中，其動(dòng)彈性模量的變化幅度逐漸趨于平緩，這是試樣隨著循環(huán)次數(shù)而不斷壓密的結(jié)果。隨著圍壓的不斷增大，其動(dòng)彈性模量也在不斷增加，在圍壓為6 MPa時(shí)達(dá)到最高值。隨著振動(dòng)次數(shù)的不斷增加，試樣在各個(gè)圍壓下的動(dòng)彈性模量都表現(xiàn)出下降的趨勢(shì)，試樣2-1、2-2和2-3的動(dòng)彈性模量分別下降了9.4%、18%和17%，表明試樣在循環(huán)荷載作用的過程中，內(nèi)部出現(xiàn)了不可恢復(fù)的損傷，并且在每30次荷載上限改變的時(shí)刻，其動(dòng)彈性模量都會(huì)發(fā)生一次突變，變得很低，并隨著振動(dòng)再緩緩升高趨于平緩，這是因?yàn)樵嚇釉谑艿捷^大的力的作用下，其內(nèi)部的微裂隙會(huì)發(fā)生擴(kuò)展，使得試樣的彈性模量降低，但保持該荷載上限不變，繼續(xù)振動(dòng)下去，其裂隙不斷被壓縮，變得緊密，從而使得彈性模量慢慢恢復(fù)平穩(wěn)的狀態(tài)。另外，取動(dòng)彈性模量鋸齒狀的最大值和最小值之差作為其平穩(wěn)度的大小參數(shù)，在圍壓為0 MPa時(shí)，其值約為0.33，3 MPa時(shí)約為0.17而6 MPa時(shí)約為0.1，隨著振動(dòng)次數(shù)的增加，圍壓為0 MPa時(shí)的動(dòng)彈性模量的平穩(wěn)度較其3 MPa和6 MPa相比較低，鋸齒狀的形態(tài)較為明顯，從而可以推出，圍壓對(duì)試樣有著束縛穩(wěn)定的作用。

5 阻尼比分析

試樣總共進(jìn)行240次振動(dòng)，其中每30次軸向荷載的上限增加10%，最多增加到其相同環(huán)境抗壓強(qiáng)度σr的80%。取每次軸向荷載改變之后的第1、5、10、15、20、25次的滯回環(huán)進(jìn)行阻尼的計(jì)算，其結(jié)果曲線見圖8。

從圖中可以看出，圍壓的不同對(duì)試樣阻尼比的影響情況也不同，隨著圍壓的增加試樣的阻尼比呈減少趨勢(shì)，在每一次軸向荷載改變的時(shí)刻，試樣的阻尼比都會(huì)呈現(xiàn)大幅的增加，并且單軸條件下的增量遠(yuǎn)大于其三軸條件。其原因是圍壓對(duì)于試樣的變形和內(nèi)部裂隙的發(fā)展有著抑制的作用，當(dāng)軸向荷載增加的時(shí)候，試樣內(nèi)部的微裂隙開始擴(kuò)展，使得整體的阻尼比變大，為裂紋擴(kuò)展階段。在單軸條件下，由于沒有圍壓的抑制作用，其內(nèi)部微裂隙的擴(kuò)展程度大于有圍壓條件下的試樣，產(chǎn)生了阻尼比的增加幅度不一致的現(xiàn)象。由圖中可以看出，在相同的軸向荷載下，試樣的阻尼比隨著振動(dòng)次數(shù)的增加，逐漸下降趨于平緩，可以推斷出在荷載循環(huán)的過程中，試樣內(nèi)部的微裂隙和晶體的排列不斷變得緊密，原生裂紋的擴(kuò)展和新裂紋的產(chǎn)生過程停止，整個(gè)試樣轉(zhuǎn)向壓密階段。隨著循環(huán)次數(shù)的增加，試樣的阻尼比呈上升的趨勢(shì)，阻尼比是與巖石內(nèi)部的裂紋擴(kuò)展和萌生有關(guān)的，巖石內(nèi)部越破碎，其塑性應(yīng)變?cè)饺菀装l(fā)生，阻尼比也越大，從而表明，隨著應(yīng)力幅值的不斷增大，巖石內(nèi)部裂紋越發(fā)育，巖石損傷越嚴(yán)重。

6 結(jié)論

a) 巖石為非理想彈性體，所以其動(dòng)應(yīng)力與動(dòng)應(yīng)變響應(yīng)在時(shí)間上并不完全對(duì)應(yīng)，兩者之間有一定的時(shí)間差，在循環(huán)荷載的作用下，卸載段曲線與加載段曲線不重合，卸載段低于加載段，出現(xiàn)滯回環(huán)。隨著應(yīng)力幅值的增大，滯回環(huán)的面積在不斷增大，其振動(dòng)一個(gè)周期所消耗的能量在增長，表明試樣損傷情況加劇。

b) 在單軸情況下，滯回環(huán)有不同程度的內(nèi)凹。隨著圍壓的增加，滯回環(huán)形態(tài)逐漸變得飽滿后變得略微外凸。表明圍壓對(duì)其滯回環(huán)的形態(tài)有影響。

c) 圍壓的增加，其試樣的軸向應(yīng)變呈下降趨勢(shì)，表明圍壓抑制試樣的變形，隨著循環(huán)過程進(jìn)行，應(yīng)力幅值不斷增加，試樣應(yīng)變曲線呈初始、穩(wěn)定和加速3個(gè)階段。加速階段的應(yīng)變曲線的明顯上翹是試樣內(nèi)部損傷加劇的結(jié)果。

d) 試樣隨著循環(huán)荷載，應(yīng)力幅值不斷增大，在全過程動(dòng)彈性模量變化曲線中發(fā)現(xiàn)：動(dòng)彈性模量Ed呈階梯狀下降；隨著圍壓的增加，動(dòng)彈性模量也在增加。在每一次應(yīng)力幅值循環(huán)中，其動(dòng)彈性模量經(jīng)歷先減少后增加并趨于穩(wěn)定的過程，表明循環(huán)荷載在一定程度上可以使試樣動(dòng)彈性模量升高，這與阻尼比所顯示的現(xiàn)象是一致的。在循環(huán)荷載過程中，試樣阻尼比隨著圍壓的增加而降低，可知圍壓抑制了試樣的破壞。