車削過程穩定性分析研究進展

秦雷　劉二亮　邢宏偉　趙立國

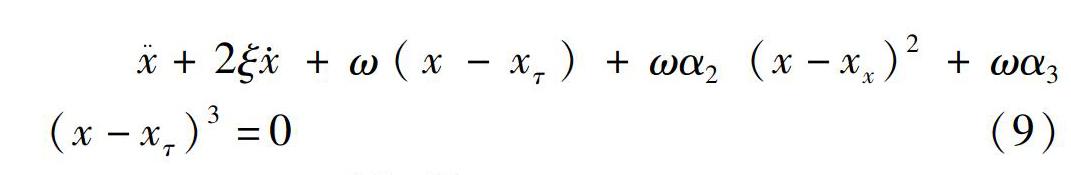
摘要：車削過程中顫振導致的車削失穩會對機床和刀具壽命、加工效率和加工表面質量造成極為不利的影響。為了提高車削加工的效率和質量，對車削過程進行穩定性分析并獲取無顫振車削條件成為了一項非常重要的研究內容。分析了顫振的產生機理，綜述了車削過程的頻域和時域穩定性分析方法，并回顧了鋸齒形切屑驅動的車削失穩研究進展，總結了當前顫振分析尚存在的主要問題，并探討未來的研究方向。

關鍵詞：

車削過程;顫振分析;頻域法;時域法;鋸齒形切屑

DOI：10.15938/j.jhust.2019.01.003

中圖分類號： TG501

文獻標志碼： A

文章編號： 1007-2683（2019）01-0014-09

Research Progress on Stability Analysis of Turning Process

QIN Lei?1，LIU Er?liang?2，XING Hong?wei?2，ZHAO Li?guo?2

（1?Spacecraft Reasearch and Development Center， Shanghai Institute of Satellite Engineering，Shanghai 200240， China;?2?School of Machanical and Power Engineering Harbin University of Science and Technology， Harbin 150080， China）

Abstract：During the turning process， the instability caused by chatter will cause a very bad influence on the life of the machine tool and the cutting tool， the machining efficiency and the surface quality?In order to improve the efficiency and quality of turning process， it is a very important content to study the stability of turning process and obtain the condition of chatter free turning?In this paper， the mechanism of chatter is analyzed， the stability analysis methods of frequency domain and time domain in turning process are summarized， the main problem existing in the flutter analysis are summarized and the future research direction is discussed

Keywords：the turning process; flutter analysis; frequency domain method; time domain method; serrated chip

0引言

機械制造業是體現一個國家整體工業發展水平的重要標志，車削加工在其中占據了舉足輕重的地位，尤其在航空、航天，船舶和醫療等科技含量較高的領域，由于材料的難加工性和零件的復雜性，車削加工因其結構簡單、適應性強等優點愈來愈受到重視[1-3]。然而，由于機床的固有特性和車削過程中的動態特性引起的車削顫振會使得車削系統失穩，直接影響零件的尺寸精度和表面質量，而且加劇刀具的磨損和破損，最終導致車削加工效率降低[4-5]。

顫振的發生和發展規律非常復雜，為實現完全地無顫振穩定加工，在過去的半個多世紀，科研人員

對其進行了大量的研究，Tobias[2]和Tlusty[3]發現再生效應是導致顫振發生的主因，奠定了再生型顫振的理論基礎。Merrit[4]以反饋控制理論為基礎，針對再生型顫振首次提出了穩定性葉圖（Stability Lobe Diagram，SLD）。后來的研究者多以此為根據，進一步擴展加深，逐漸形成了一整套再生型顫振理論體系[6]。為簡化車削系統起見，設其是一個單自由度系統，如圖1（a）所示，考慮車削過程中由瞬時車削厚度?s（t）?引起的動態車削力?F（t）?，得到單自由度系統車削動力學模型：

m?x¨?t+c?x·?（t）+kx（t）=K?f·b·[x（t-T）-x（t）]（1）

式中：kf為徑向車削系數;b為車削寬度;T為本次車削振紋與上次車削振紋之間的時間延遲，為由刀具振動而導致的動態切屑厚度;m、c和k?分別為振動系統的模態質量、模態阻尼和模態剛度。

另一方面，一些學者認為，鋸齒形切屑的形成同樣與顫振有著密不可分的關系，由于車削過程中的熱軟化效應[7-11]，切屑形成過程中的鋸齒化會周期性地釋放絕熱剪切力，引起車削力的動態變化[11]，進而導致顫振的發生。該理論雖然提出已久，但目前在這方面的研究還處在相對基礎的階段。Cook[12]最早對鋸齒形切屑形成與顫振之間的關系進行研究。隨后，Eliasberg[13]采用高速攝影技術對車削過程進行監控，得出了切屑折斷的同時伴隨顫振產生的結論。以此開始，經過學者們的不斷探索，逐漸成為了車削振動研究的重要組成部分。

針對以上兩種車削顫振理論，結合現代車削加工高精、高效的宗旨，本文對車削過程顫振的研究脈絡進行了梳理，針對車削顫振的時域和頻域兩種分析方法，綜述其研究進展，同時回顧了鋸齒形切屑誘導的車削顫振研究現狀，分析現有研究的不足，提出了未來研究的方向。

1車削顫振頻域法的研究進展

頻域法又稱解析求解法，即為在頻域內對車削系統穩定性進行分析求解的方法。其基本過程是：依據簡化后的動力學系統，建立車削系統動力學微分方程;考慮再生效應對動態車削厚度的影響，基于Floquet理論和Fourier級數展開理論推導動態車削力，近似求解時變的車削力方向系數;對系統的特征方程進行求解，并根據Lyapunov穩定性判據判別其穩定性;求解臨界穩定條件下的軸向切深和主軸轉速，并繪制穩定性極限圖。其中，根據Fourier 級數展開時諧波數選取的不同，頻域法又可分為0 階頻域解析法[14]和多頻域法[15]。

頻域法作為車削系統穩定性離線預測分析的一種重要方法，主要包括SLD法[16-17]和Nyquist圖法[18]。

1?1SLD法

SLD法以位移導納函數為基礎獲取對應車削系統的顫振穩定曲線，通過標記極限車削寬度blim與機床主軸轉速?N?之間的關系，將（N?blim）平面分為穩定車削區和不穩定車削區，給出車削系統的穩定情況[19-20]。該方法是目前應用最為廣泛的一種穩定性離線預測方法，其理論基礎如下：

將式（1）適當變形后進行拉普拉斯變換，得到振動系統的頻率響應函數：

Γ（s）=1s?2+2ξω?n+ω?2?n（2）

其中：ω?2?n=km，且cm=2ξω?n;而由s=jω，獲取出傳遞函數的實部和虛部分別為

G（s）=ω?2?n-ω?2R（ω）（3）

H（s）=-（2ξω?n）ωR（ω）（4）

式中：ω為顫振頻率

R（ω）=?（ω?2?n）?2+?（2ξω?n）?2ω?2 （?Denominator?）（5）

車削過程從穩定車削到顫振的極限車削寬度可由下式表示[19]：

b??lim?=-12K?fG（ω）（6）

T=1ω（2n?π?+θ）（7）

N=60/T（8）

其中：θ為相變角，T?為主軸旋轉周期。極限車削寬度?b?lim?僅與系統的動態特點、工件材料，車削速度和進給量以及刀具的幾何形狀有關[20]。

綜上所述，由式（6）～（8）繪制出描述極限車削寬度?b?lim?與主軸轉速?N?之間關系的穩定性葉圖，如圖1所示。

分析穩定性圖可以指導車削過程選擇合理的車削參數，找到最大無顫振材料去除率加工參數的特定組合（圖中穩定區）[20-23]。該方法的提出，標志著顫振分析理論趨于成熟。

王曉軍[23]研究了極限車削寬度隨機床主軸轉速的變化關系，對車削加工系統穩定性極限的最小極限車削寬度值和不穩定車削轉速區段進行了預測，并分析重疊系數?μ、方向系數u以及主振系統阻尼比ξ?等對極限車削寬度?b?lim?的影響規律。林濱等[24]把工件視為弱剛性體、刀具視為剛性體，提出嚴格穩定區的概念，得到嚴格穩定性極限圖。張勇等[25]建立了外圓車削顫振模型，描述了含重合度不為1的條件下穩定性葉圖的繪制過程。李金華等[26]通過穩定性葉圖，分別分析了主軸轉速、車削重疊系數、主振系統阻尼比、車削剛度系數、主振系統剛度系數和方向系數對車削系統穩定性的影響。汪博等[27]利用三維穩定性葉圖、極限車削深度和葉瓣交點隨參數的變化曲線表征車削力幅值、轉速及阻尼比等參數對車削穩定性的影響規律，為優化加工工藝、提高系統車削穩定性提供理論依據。李忠群等[28]通過開發Matlab仿真程序建立了考慮過程阻尼的穩定性葉圖，并得出過程阻尼會顯著提高低速區車削穩定性的結論，以此可指導航空難加工材料的高效車削。

G?Urbicain[29]針對車削Inconel 718的穩定性圖，提出了預測縱向顫振無顫振區的方法。建立了一個1/2自由度動態模型以獲取縱向模式對再生平面切屑再生影響的規律。Hajmohammadi[30]采用有限元仿真的方法針對車削刀具的單自由度模型模擬了在正交條件下熱-力切屑形成的動態相互作用，研究了摩擦、塑性變形、熱形成和過程阻尼對顫振形成的影響，并探明了如何提高車削區的溫度可影響顫振發生。Gerasimenko[31]以壁管零件車削過程為研究對象，觀察分析顫振車削過程的瞬態記錄，得出了刀具運動對應車削力模態投影變化的結論，并考慮車削過程中的零件幾何變化，對間歇不連續顫振頻率的演變進行分析，獲取了穩態車削條件。Otto[32]針對柔性工件車削過程中車削點的不同，提出了一種動力學分析的通用性模型，確定了依賴位置車削的顫振穩定性葉圖，實現了一種快速、精確、系統地車削過程穩定性分析。

然而，穩定性葉圖法的缺點也不容忽視，總結以下3點：①SLD隨機床、工件材料和刀具的變化而變化，使分析變得繁瑣;②由于車削過程采用靜態模型，所以基于SLD法的任何解析技術都不能獲得很高的穩定特性;③實際應用中難以獲得加工過程中動態力、位移等參數的時間歷程，也難以在高性能數控系統中進行集成，限制了該方法的廣范應用。

1?2Nyquist圖法

Nyquist圖法的核心內容是奈奎斯特判據，其特點是根據開環系統頻率特性來判斷閉環系統的穩定性，應用該方法不必求解閉環系統的特征根就可判別系統的穩定性。

Minis[33]等提出了一種應用于二維正交車削的穩定性判定方法，該方法通過確定奈氏曲線與負實軸的最左交點，采用奈奎斯特判據來推導臨界穩定性參數。Altintas[34]等采用奈奎斯特判據確定了動態車削力系數，并以此為基礎分析了車削速度、刀具磨損、振動的頻率和波長對顫振的影響。Turkes[35]應用定向傳遞函數和奈奎斯特準則的分解形式，對單自由度模型進行了線性分析。

由于奈奎斯特圖法僅可以用來判定給定車削條件的穩定性，故應用面較窄。

2車削顫振時域仿真法的研究進展

頻域模型是一種基于線性理論的解析算法，無法預測諸如過程阻尼和大振幅下刀具脫離加工表面等非線性情況，并且在對其隨時間周期變化的方向動態車削系數進行傅里葉近似時只取了直流分量，這就導致頻域穩定性圖的預測精度降低[36]。為了提高顫振穩定域的仿真精度，出現了仿真精度高但仿真時間長的時域穩定域仿真算法。

時域仿真法，是指在時間域內對車削過程穩定性進行分析、仿真，直接獲得振動量和進給力時間歷程的方法，可分為數值法和解析（半解析）法[37]。其核心內涵是：應用數值方法（Eular法或Runge?Kutta法）近似求解車削系統動力學微分方程，在求解微分方程時需要將連續時間變量離散化;根據已知初始條件以足夠小的時間增量對其進行迭代求解，獲得系統動力學特性的時域解。時域仿真方法可以綜合考慮諸如刀具幾何、多維結構動力學及非線性過程增益等因素對加工過程穩定性的影響，故預測精度較高。

2?1數值法

數值法的本質是直接求解原始時滯微分方程獲取車削過程動態響應的時間歷程，再根據此響應的振動幅值是否發散（或者由響應構造的時域穩定判據）來確定加工過程的穩定性。其中，時域穩定性判據主要有以下幾種：①FFT 法;②峰值力（簡稱PTP）法;③動態力—靜態力法;④刀尖位移統計方法[37]。

FFT法的基本思想是對時域仿真數據作FFT 變換，根據車削頻率及其諧振頻率下的幅值在所有頻率范圍的幅值之和中所占比例?ηp?作為顫振發生的標準，當?ηp?<0?8 時可認為存在顫振;PTP 法基于車削條件接近穩定邊界時車削力峰值會急劇增大的思想;動靜態力法是將相同車削參數下柔剛性系統的最大車削力之比?ηF?作為判定標準，當?ηF?>1?3時認為存在顫振;刀尖位移統計方法是指工件每旋轉一周采集一次刀尖位移數據，然后使用其樣本統計方差作為顫振判定標準。

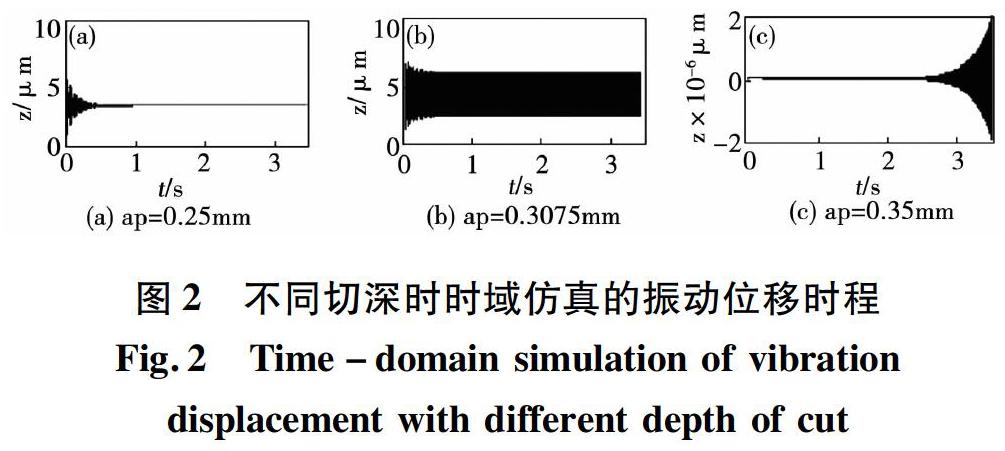
林潔瓊等[38]基于互四階累積量的諧參數聯合估計TLS?ESPRIT方法，探討再生型車削系統動態響應的頻率、相鄰兩轉車削間相移和互功率的辨識，揭示了在動態失穩車削中這些諧參數的演變特征以及多頻再生型車削顫振現象。韓賢國[39-40]考慮被加工軸的直徑和質量變化對顫振的影響，針對車削過程中工件受軸向移動三維車削力的動態作用，建立了車削軸的振動力學模型，采用Matlab軟件求得振動模型運動方程的數值解，得到了在不同車削條件下直徑和質量隨時間變化的軸的振動響應。魯燕等[41]通過理論推導及數值求解，得到細長軸類零件車削的振動響應，通過仿真揭示車削參數及工件尺寸的變化對振動響應幅值的影響規律。劉宇等[42]采用一種變步長方法進行時域仿真研究，該算法可以根據計算點主軸轉速動態調整仿真步長，保證算法收斂，滿足仿真結果精度要求。當車削深度取不同值時，由時域仿真算法獲得位移時程如圖2所示。

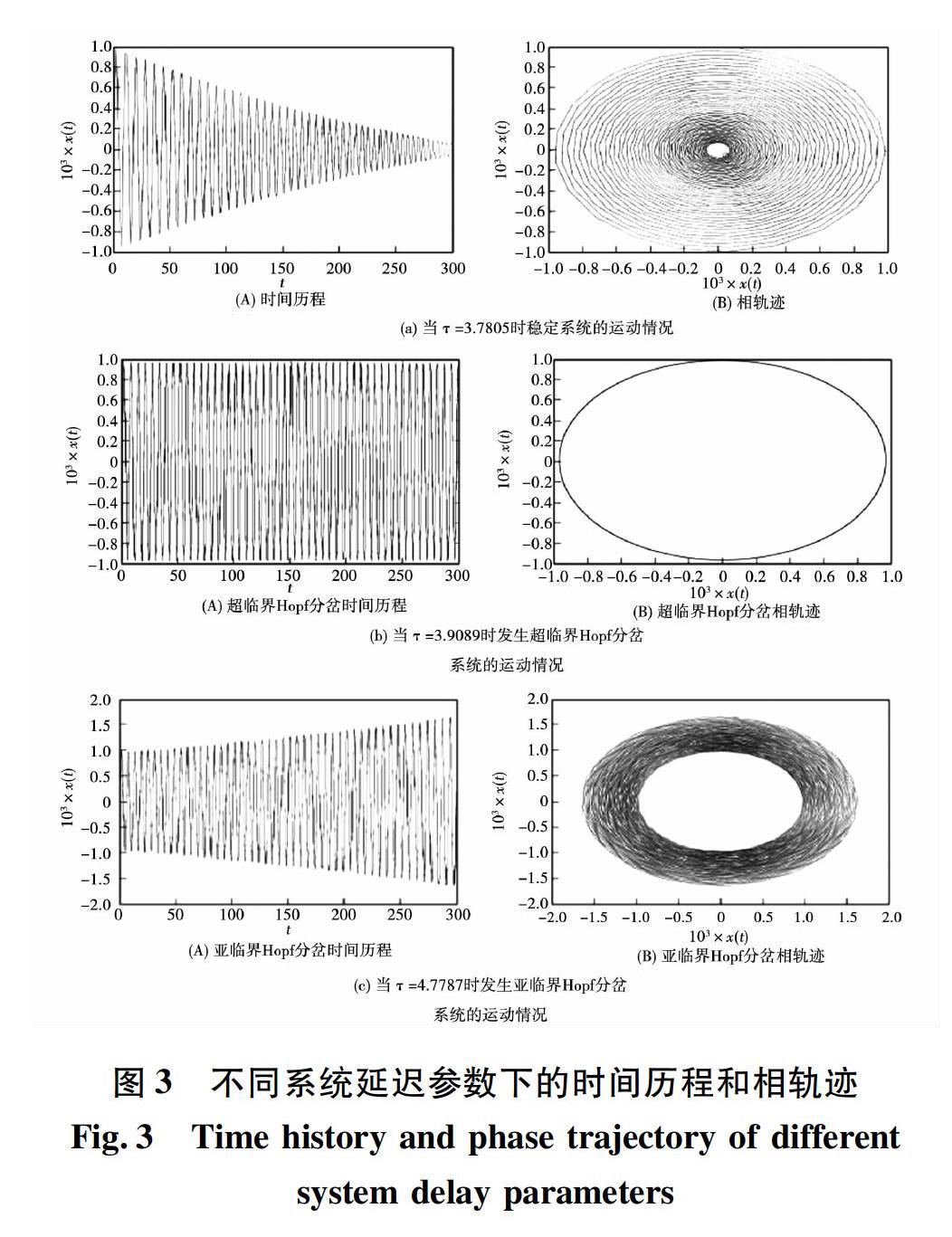
Huang Cheng?Hung[43]基于共軛梯度法（CGM）（或迭代正則化方法），采用Euler?Bernoulli梁代替車削刀具以研究車削過程振動的逆問題，評估了刀具的依賴于空間和時間的外部力，并進行了數值仿真。李鵬松[44]等人利用多尺度法分析系統時滯參數對解穩定性的影響，并針對Hanna單自由度無量綱形式的振動方程（式9）得到了系統延遲參數?τ?∈（0， 3?9088）、?τ?∈（3?9089， 3?9105）和?τ?∈（3?9106，5?4684）時的時間歷程和相軌跡，如圖3所示。

x¨?+2ξ?x·?+ω（x-x?τ）+ωα?2?（x-x?x）?2+ωα?3?（x-x?τ?）?3=0?（9）

G?Urbikain[45-46]首次采用Chebyshev配置法（見圖4）建立車削穩定性模型，考慮刀具導向角和非線性車削系數對穩定區的影響提出了一種基于Matlab dde23程序和時域仿真的穩定性分析技術。Tavari[47]提出了一種新的車削顫振的三維非線性模型。將工件建模為一個被車削力激發的旋轉懸臂梁。采用π?Buckingham理論提取這個問題的無量綱參數。利用這些參數，建立了無維數運動方程。得到了該非線性問題的近似解析解。確定了對于穩定和不穩定的車削速度間隔。

數值法時域仿真計算可以考慮非線性車削力、刀具振動時的時變徑向浸入邊界等復雜的非線性效應，目前應用較廣，但其計算效率比解析（或半解析）法低得多。

2?2解析（半解析）法

解析（或半解析）法的本質是通過對原始時滯微分方程做合理的近似，構造有限維單值算子逼近無限維單值算子，從而降低穩定性分析難度、提高計算效率。

李明霞等[48]提出了一種完全離散化方法，通過離散化方法將車削模型中的時域因子，微分因子，時延因子均離散化，實現了真正的全部因子離散化的目標。謝奇之[49]提出了一個具有平方結構剛度和立方再生項的弱非線性模型來表達加工過程中的自激振動，通過使用規范形方法和中心流形理論給出了判斷Hopf分岔方向和周期解穩定性的公式。Kotaiah[50]提出了一種基于遺傳算法和神經網絡模型的預測局部穩定車削參數的內圓車削優化方案，如圖5所示，該方案將車削力、表面粗糙度和臨界顫振位置建模為包括刀具懸伸長度在內的一個變量的函數，采用徑向基函數神經網絡開發了一般化的模型，并利用二進制編碼遺傳算法預測最佳車削參數。

Frumu?anu[51]為了對動態演化過程建模，首先，將記錄特征值的連續時間序列，被分為相等的序列，拼湊成一個特征圖，如圖6所示。其中，每一行代表工件完整一轉，每個矩形代表一個由特征值表征的車削力信號序列。這張圖上的當前窗口包括?m?行（對應于工件當前轉之前的最后?m?轉）和另l行（下l轉），這?m?行構成用于模型修正的數據集而l行定義目前更新的模型將被用于預測的區域。基于此種方法，建立線性模型和神經網絡模型，并開發了用于顫振監測預報的智能系統。

Kim Pilkee[52]為探討狀態相關延遲的非線性車削系統的顫振特性，考慮了非線性剛度和非線性車削力，得到了穩定性邊界，并采用多尺度和諧波平衡的方法進行分岔分析，解釋了狀態時滯對車削系統振幅的影響。Ding Ye[53]針對多時滯多自由度二階系統的線性穩定性分析提出了一種半解析解的微分求積法（DQM），基于一維Mathieu方程（式10），通過將任意離散時間點狀態向量的導數表述為該狀態向量值的一個線性加權，將原始的時滯微分方程近似為一組代數方程以得到Floquet轉換矩陣，基于Floquet理論，通過檢查轉換矩陣的特征值確定系統的穩定性，如圖7所示，其中灰色陰影為不穩定時滯組合區。

x¨?（t）+a?1?x·（t）+δx（t）=b?0，1?x（t-τ?1）+b?1，2?x·（t-τ?2）?（10）

需要說明的是，直接通過試切實驗獲取振動信號也可以判斷加工過程的穩定性。這類方法的優點是無需建立動力學模型，如根據加工過程的車削力信號[54]或者加速度信號[55]來判斷是否發生顫振。但這類方法的缺點也明顯：需據不同的加工參數做很多組試切實驗才能確定工藝參數穩定邊界，實驗工作量極大。

3切屑引起的車削顫振的研究進展

隨著航空航天工業的飛速發展，具有較高比強度和耐磨性的難加工材料[56]逐漸成為了研究的熱點。但與此同時較低的熱導率和材料的熱軟化性將導致車削過程中鋸齒形切屑的產生，鋸齒形切屑的產生過程伴隨著絕熱剪切力的周期性釋放，引起車削力動態變化，降低車削過程的穩定性，使顫振依然無法避免。

關于鋸齒形切屑的形成與刀具振動的關系已研究多年，研究者力求建立一種鋸齒頻率-車削參數模型用以預測顫振。其中，Bayoumi和Xie[57]研究發現，鋸齒屑鋸齒長度與進給量近似成比例，而車削速度對其無明顯影響。文東輝[11]探討了鋸齒形切屑生成頻率與車削力頻率的關系，應用小波分析從車削力高頻信號特征判斷是否產生鋸齒形切屑以及鋸齒形切屑的剪切失穩。徐銘等[58]依據Shaw 建立的鋸齒生成頻率模型，分析得出：精密硬態車削條件下，鋸齒形切屑的生成頻率要遠小于車削力高頻信號的頻率。Komanduri和Von Turkovich[59]觀察Ti6Al4V車削過程中的圖像，描述了鋸齒形切屑形成過程的階段，并發現在其形成的過程中車削力和相對于刀具的車削速度震蕩明顯。

Nurul Amin[60]研究了鋸齒形切屑對振動的影響，發現鋸齒形切屑的形成會使刀具、主軸分別或者兩者同時激發，并以高幅振動。El Mansori[61]發現，隨著通過磁輔助控制車削過程來控制鋸齒形切屑形成，刀具壽命明顯提升，證明了切屑鋸齒形頻率對刀具表面的沖擊影響。Sun等[62]對Ti6Al4V車削鋸齒形切屑進行研究，發現當進給量等于或大于0?149.mm/r時，車削力的震蕩頻率與車削速度成正比例，與進給量成反比，而與切深關系不大。同時發現，當鋸齒形頻率近似等于于車削系統某部件一階模態整數倍時，系統產生了大振幅的振動。Amin?[63]和Patwari[64-66]提出振動的根本原因是鋸齒形成失穩頻率機床車削系統某薄弱組件固有頻率一致。而Amin[67]研究車削過程時發現，當切屑的初級或二級鋸齒頻率恰好等于系統薄弱環節固有頻率時，由于共振導致系統產生高幅振動。U?Patwari[68]通過銑削實驗與模態仿真同樣得到了相似的結論。

Landberg[69]以鋸齒形切屑為研究對象，建立了切屑鋸齒化頻率與車削速度的關系模型，探討了切屑形成導致的車削振動。Doi和Ohhashi[70]提出了一種鋸齒形切屑驅動的振動預測的建模方法，采用Mathieu方程來預測車削失穩條件。Morehead等[71]人同樣在鋼車削過程中研究了鋸齒性切屑。Chris M?Taylor[72]采用Labview仿真了單位車削寬度的振幅與車削參數的關系（見圖8），并基于文獻[57，60，62]提出了一種車削過程中鋸齒形切屑驅動振動的振幅預測模型，該模型將振幅建模為車削參數的函數，得到振幅的預測模型為

a?X=G（2?π?V60λ?0s）K（V）bsn（11）

a??max?=sλ?0?tan?α2?π?（12）

式中：a?X為進給x方向顫振振幅（?mm?）;a??max?為極限振幅（?mm?）;G（ω）為進給方向頻響函數;V為車削速度（?mm/min?）;b為車削寬度（?mm?）;s為進給量（?mm/r?）;α為刀具后角;n為振幅修訂系數;λ?0為由試驗獲得的無量綱鋸齒屑波長系數。

.切屑分析技術是一種離線的基于實驗的顫振分析手段，可以通過將切屑的形態特點與顫振的某些參數，如動態車削力或顫振頻率建立聯系來分析顫振系統的穩定性，然而目前的鋸齒形切屑分析技術只能在振動實際產生之后提供顫振的相關信息，而無法提前預測顫振的發生。然而隨著研究的深入，通過切屑分析建立車削條件-顫振的關系模型以指導生產同樣具有光明前景。

4結論與展望

自20世紀初至今，國內外學者對車削顫振進行了大量的研究，取得了眾多的研究成果，已滲透到力學、控制科學與工程和計算機科學與技術等多個學科，并衍生出多個交叉學科主題。學者們提出了各種各樣的分析與預測顫振的手段與方法。本文回顧了部分關于車削顫振分析的文獻，并從頻域解析，時域仿真和鋸齒形切屑分析三方面入手，以車削振動模型為依托，介紹了當前顫振分析技術的主要方法以及關鍵研究成果。然而，由于工件形狀的日益復雜化，工件材料的日益特殊化，同時對加工精度與加工效率的要求也日益提高，因此，對于顫振問題的研究，現在雖已深入，但還不夠完善，隨著基礎理論的透徹和新穎手段的應用，車削顫振的研究逐漸出現了新的視角和方向：

1）在完善再生型顫振研究的基礎上，進行車削過程多顫振并存分析并尋求新的顫振機理。

2）立足于鋸齒形切屑的產生機理及其與車削顫振的頻率關系，探索用于分析預測鋸齒屑驅動顫振的穩定性模型，以實現難加工材料的車削參數優化。

3）在逐步豐滿線性模型的基礎上，考慮車削過程中力、熱、變形以及刀具磨損甚至其他影響因素相互聯系和作用導致的復雜性，研究車削過程中非線性多自由系統精確求解方法，以獲得多維車削顫振穩定域并實現同步預報。

4）針對當前高速車削技術不能科學、有效地控制車削過程振動而嚴重影響加工質量及生產率的瓶頸限制，構建基于高速車削穩定性理論和實驗研究的高速車削穩定性數據庫，以實現高速車削數據查詢、車削穩定性評價、控制和優化等功能。

參 考 文 獻：

[1]于駿一，吳博達.機械加工振動的診斷、識別與控制[M].北京：清華大學出版社，1994.

[2]TOBIAS SA. Machine Tool Vibration[M]. Glasgow： Blackie and Sons Ltd， 1965.

[3]KOENIGSBENGER F， TLUSTY J. Machine Tool Structures-Vol.1：Stability Against Chatter[M]. New York： Pergamon Press， 1967.

[4]MERRIT HE. Theory of Self?excited Machine Tool Chatter[J]. ASME Journal of Engineering for Industry， 1965， 87： 447-454.

[5]SIDDHPURA M， PAUROBALLY R. A Review of Chatter Vibration Research in Turning[J]. International Journal of Machine Tools & Manufacture， 2016， 61：27.

[6]李有堂.機械振動理論與應用[M].北京：科學出版社，2012.

[7]蘇國勝.高速車削鋸齒形切屑形成過程與形成機理的研究[D].濟南：山東大學，2011.

[8]楊奇彪.高速車削鋸齒形切屑的形成機理及表征[D].濟南：山東大學，2012.

[9]王敏杰，谷麗瑤.高速車削過程絕熱剪切局部化斷裂判據[J].機械工程學報，2013， 49（1）：156.

[10]岳彩旭，劉獻禮，嚴復鋼，等.不同刃口形式下鋸齒形切屑形成過程的仿真與實驗[J].機械科學與技術， 2011， 30（4）： 673.

[11]文東輝.PCBN刀具硬態車削機理及技術[D].大連：大連理工大學， 2002.

[12]COOK NH. Chip Formation in Machining Titanium[J]. In Proc. symp. Machining and Grinding Titanium， Watertown， MA， USA， 1953：1.

[13]ELIASBERG ME. Fundamentals of the Theory of Chatter During Metal Cutting Process[J]. Stanki i Instrumenti， 1962（10）： 3.

[14]BUDAK E. The Mechanics and Dynamic of Milling Thin?walled Structures[D]. University of British Columbia， 1994.

[15]MERDOL SD， ALTINTAS Y. Muti Frequency Solution of Chatter Stability for Low Immersion Milling[J]. Journal of Manufacturing Science and Engineering， 2004， 126： 459.

[16]BUDAK E， OZLU E. Analytical Modeling of Chatter Stability in Turning and Boring Operations： A Multi?Dimensional Approach[J]. Annals of the CIRP Vol， 2007， 56（1）：401.

[17]EMRE Ozlu， ERHAN Budak. Analytical Modeling of Chatter Stability in Turning and Boring Operations—Part II： Experimental Verification[J]. Journal of Manufacturing Science and Engineering， 2007，129： 733.

[18]徐燕申， MINIS I. E.， MAGRAB E. B.車削加工系統的穩定性分析[J].振動工程學報， 1990， 3（1）： 64.

[19]ALTINTAS Y. Manufacturing Automation[M]. Cambridge： Cambridge University Press， 2000.

[20]GUILLEM Quintana， JOAQUIM Ciurana. Chatter in machining processes： A review[J]. International Journal of Machine Tools & Manufacture， 2011，51： 363.

[21]GIOVANNI Totis， MARCO Sortino， Robust Analysis of Stability in Internal Turning[J]. 24th DAAAM International Symposium on Intelligent Manufacturing and Automation， Procedia Engineering， 2014， 69： 1306.

[22]趙宏偉，王曉軍，于駿一.再生型機床車削顫振系統穩定性極限預測[J]. 精密制造與自動化， 2003（S1）： 62.

[23]王曉軍.車削加工系統穩定性極限預測的研究[D].濟南：山東大學， 2005.

[24]林濱，陳東，韓植林，等.鋁合金薄壁圓柱殼車削穩定性研究[J].兵工學報， 2012， 33（7）： 847.

[25]張勇，合燁，陳小安.基于MATLAB/Simulink再生車削顫振仿真研究[J].機械研究與應用， 2016， 26（2）：23.

[26]李金華，謝華龍，盛忠起，等.數控車削過程再生型顫振穩定性建模與仿真[J].東北大學學報（自然科學版）， 2013， 34（1）：118.

[27]汪博，孫偉，聞邦椿.高速主軸系統車削穩定性預測及影響因素分析[J].機械工程學報， 2013， 49（27）：18.

[28]李忠群，董亞峰，夏磊，等.考慮過程阻尼的車削穩定性建模與仿真分析[J].湖南工業大學學報， 2014， 28（6）： 23.

[29]URBICAIN G， PALACIOS J. A.， FERNNDEZ A， et al. Stability Prediction Maps in Turning of Difficult?to?cut Materials[J]. The Manufacturing Engineering Society International Conference， MESIC 2013， Procedia Engineering， 2013，63： 514.

[30]MOHAMMAD.S.Hajmohammadi，MOHAMMAD.R.Movahhedy. Investigation of Thermal Effects on Machining Chatter Using FEM Simulation of Chip Formation[J]. 5th CIRP Conference on High Performance Cutting 2012， Procedia CIRP， 2012（1）：50.

[31]ARTEM Gerasimenko， MIKHAIL Guskov， DUCHEMIN Jérme， et al. Variable Compliance?related aspects of Chatter in Turning Thin?walled Tubular Parts[J]. 15th CIRP Conference on Modelling of Machining Operations， Procedia CIRP， 2015， 31： 58.

[32]ANDREAS Otto， FIRAS A Khasawneh， RADONS Günter， Position?dependent Stability Analysis of Turning with Tool and Workpiece Compliance[J]. Int J Adv Manuf Technol， 2015，79（9/12）：1453.

[33]MINIS I E， MAGRAB E B， PANDELIDIS I O. Improved Methods for the Prediction of Chatter in Turning， Part 3. A Generalized Linear Theory[J]. Journal of Engineering for Industry， Transactions ASME， 1991， 112： 28.

[34]ALTINTAS Y， EYNIAN M， ONOZUKA H. Identification of Dynamic Cutting Force Coefficients and Chatter Stability with Process Damping[J]. CIRP Annals?Manufacturing Technology， 2008， 57：371.

[35]TURKES E， ORAK S， NESELI S， et al. Linear Analysis of Chatter Vibration and Stability for Orthogonal Cutting in Turning[J]. International Journal of Refractory Metals and Hard Materials， 2016， 29：163.

[36]吳春橋，張勝文，仝永海，等. 銑削加工過程動力學建模仿真技術研究進展[J].機床與液壓， 2011， 39（19）： 121.

[37]李忠群，鄭敏.銑削過程顫振穩定域建模研究現狀與展望[J].制造技術與機床， 2013（10）： 45.

[38]林潔瓊，周曉勤，孔繁森，等.再生車削顫振系統動態響應諧參數辨識[J].吉林大學學報（工學版）， 2009， 39（4）： 964.

[39]韓賢國， 王敏杰， 歐陽華江. 車削過程中工件的振動力學建模與分析[J]. 機械強度， 2012， 34（5）： 644.

[40]韓賢國，王敏杰，歐陽華江.考慮直徑和質量變化的車削工件振動建模和試驗分析[J].大連理工大學學報， 2012， 52（4）：514.

[41]魯燕，王大中，張統超，等.細長軸車削振動影響因素研究[J].上海工程技術大學學報， 2014， 28（4）： 308.

[42]劉宇，李青祥，張義民.基于數值積分的車削加工時域仿真[J].東北大學學報（自然科學版）， 2014， 35（8）： 1189.

[43]HUANG CHENG?Hung， SHIH CHIH?Chun， KIM SIN. An Inverse Vibration Problem in Estimating the Spatial and Temporal?dependent External Forces for Cutting Tools[J]. Applied Mathematical Modelling， 2009， 33： 2683.

[44]李鵬松，盛桂全，孟永永.再生型顫振系統的Hopf分岔分析與控制[J].吉林大學學報（理學版）， 2014， 52（6）： 1155.

[45]URBIKAIN G， LACALLE L.N.Ló pez de， CAMPA F.J， et al. Stability Prediction in Straight Turning of a Flexible Workpiece by Collocation Method[J]. International Journal of Machine Tools & Manufacture， 2016（54/55）： 73.

[46]URBIKAIN G， OLVERA D， LACALLE L.N.López de， et al. Stability and Vibrational Behaviour in Turning Processes with Low Rotational Speeds[J]. Int J Adv Manuf Technol，2015，80（5/8）：871.

[47]TAVARI Hojjatollah， MOHAMMAD Mahdi Jalili， MOHAMMAD Reza Movahhedy， Nonlinear Analysis of Chatter in Turning Process Using Dimensionless Groups[J]. J Braz.Soc.Mech.Sci.Eng， 2014，37（4）：1151.

[48]李明霞，基于完全離散化方法的車削過程穩定性預測研究[D].武漢：華中科技大學， 2013.

[49]謝奇之.機床顫振的Hopf分岔及半離散算法研究[D].天津：天津大學， 2013.

[50]KOTAINAH K. Rama， SRINIVAS J， SEKAR M. Prediction of Optimal Stability States in Inward?turning Operation Using Neurogenetic Algorithms[J]. Int J Adv Manuf Technol， 2009， 45：679.

[51]GABRIEL R.Frumu?anu， ALEXANDRU Epureanu， IONUT C.Constantin. Method for Early Detection of the Regenerative Instability in Turning[J]. Int J Adv Manuf Technol， 2012， 58：29.

[52]PILKEE Kim， JONGWON Seok. Bifurcation Analyses on the Chatter Vibrations of a Turning Process with State?dependent Delay[J]. Nonlinear Dyn， 2016， 69： 891.

[53]DING Ye， NIU Jinbo， ZHU Limin， et al. Differential Quadrature Method for Stability Analysis of Dynamic Systems With Multiple Delays： Application to Simultaneous Machining Operations[J]. Journal of Vibration and Acoustics， 2015， 137：024501-1.

[54]ZHANG X J， XIONG C H， DING Y， et al. Milling Stability Analysis with Simultaneously Considering the Structural Mode Coupling Effect and Regenerative Effect[J]. Int J Mach Tool Manu， 2011， 53： 127.

[55]KATJA M.Hynynen， JUHO Ratava， TUOMO Lindh， et al. Chatter Detection in Turning Processes Using Coherence of Acceleration and Audio Signals[J]. Journal of Manufacturing Science and Engineering， 2014， 136（4）：044503.

[56]周俊，鎳基高溫合金GH4169高速車削相關技術與機理的研究[D].哈爾濱：哈爾濱工業大學， 2012.

[57]BAYOUMI AE， XIE JQ， Some Metallurgical Aspects of Chip Formation in Cutting ti?6wt[J]. Mater Sci Eng， 1995， 190： 173.

[58]徐銘，文東輝，戴勇，等.PCBN刀具車削中鋸齒形切屑形態的動態車削力識別[J]， 金剛石與磨料磨具工程， 2005（6）：62.

[59]KOMANDURI R， VON Turkovich B F. New Observations on the Mechanism of Chip Formation When Machining Titanium Alloys[J]. Wear ， 1981， 69： 179.

[60]AKM Nurul Amin， AF Ismail， NOR KhairusshimaMK Effectiveness of Uncoated Wc?co and Pcd Inserts in End Milling of Titanium Alloy?ti?6al?4v[J]. J Mater Process Technol， 2007， 185：147.

[61]El Mansori， M. Machinability of Ferromagnetic Steels by Magnetically?Assisted Cutting Process[C]// AMPT， Malaysia， 2009： 131.

[62]SUN S， BRANDT M， MS Dargusch. Characteristics of Cutting Forces and Chip Formation in Machining of Titanium Alloys[J]. Int J Mach Tools Manuf， 2009， 49： 561.

[63]AMIN A. K. M. N. Investigation of the Laws Governing the Formation of Chatter During Metal Cutting Processes and Their Influence on Tool Wear[D]. Ph.D. thesis， Georgian Polytechnic Institute， Tbilisi， GA， 1982.

[64]PATWARI A. U.， AMIN A. K. M. N.， FARIS W. F.， et al. Investigations of the Causes of Chatter in Computer Aided Manufacturing Process During End Milling Operation[C]// Proceedings of the Third International Conference on Mechatronics 2008， Faculty of Engineering， International Islamic University of Malaysia， 2008： 416.

[65]PATWARI A. U.， AMIN A. K. M. N.， FARIS W. F.， Role of Chip Serration Frequency in Chatter Formation During End Milling Operation of Stainless Steel[J]. Journal of Advanced Materials Research AMR， 2016 （97/101）： 1989.

[66]PATWARI， A. U.， AMIN， A. K. M. N.， et al. Identification of Instabilities of Chip Formation and Its Prediction Model During End Milling of Medium Carbon Steel （S45C）[J]. American Journal of Engineering and Applied Sciences， 2010， 3（1）： 193.

[67]NURULAMIN， A. K. M.， JAAFAR， I.， PATWARI， A.， et al. Role of Discrete Nature of Chip Formation and Natural Vibrations of Prominent System Components in Chatter Formation During Metal Cutting[J]. IIUM Engineering Journal，2010，11（1）：124-138.

[68]PATWARI Md. Anayet U， AMIN A. K. M. Nurul， FARIS Waleed F. Influence of Chip Serration Frequency on Chatter Formation During End Milling of Ti6Al4V[J]. Journal of Manufacturing Science and Engineering， 2011， 133：011013-1.

[69]LANDBERG P. Vibrations Caused by Chip Formation[J]. Microtechnic， 1956， 10（5）： 219.

[70]DOI M， OHHASHI M. A Study on Parametric Vibration in Machining of Hard Cutting Metals[J]. Int J Jpn Soc Precis Eng， 1992， 26（3）： 195.

[71]MOREHEAD MD， HUANG Y， LUO J. Chip Morphology Characterization and Modeling in Machining Hardened 52100 Steels[J]. Mach Sci Technol， 2007， 11（3）： 335.

[72]TAYLOR Chris M， SAM Turner， EVANGELOS Papatheou， et al. Modelling of Segmentation?driven vibration in Machining[J]， Int J AdvManuf Technol， 2013， 66： 207.