融合同態濾波和小波變換的圖像去霧算法研究

董靜薇　趙春麗　海博

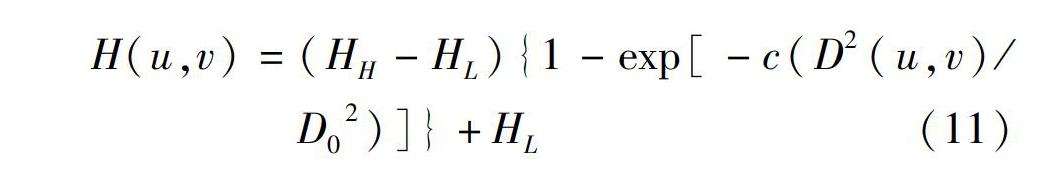
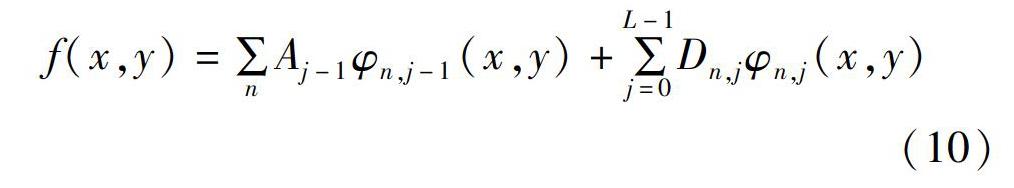
摘要：針對霧天時圖像退化嚴重，對比度低的問題，提出了一種改進算法。從時頻分析的角度出發，將同態濾波算法中的傅立葉變換用快速小波變換代替，然后在變換域內用改進的濾波器對小波系數進行處理，從而達到增強霧天降質圖像的目的。實驗結果表明，改進算法能夠有效校正霧天圖像光照，保持圖像原有信息不丟失，增強圖像的對比度，使處理后的圖像更具有可視性。

關鍵詞：同態濾波，小波變換，圖像增強，對比度

DOI：10?15938/j?jhust?2019?01?011

中圖分類號： TP391

文獻標志碼： A

文章編號： 1007-2683（2019）01-0066-05

Research on Image De?fog Algorithm Based on Fusion?Homomorphic Filtering and Wavelet Transform

DONG Jing?wei?1，2?，ZHAO Chun?li?1，2?，HAI Bo?1，2

（1.School of Measurement and Control Technology and Communications Engineering，Harbin University of Science and Technology，Harbin 150080，China;

2.Higher Educational Key Laboratory for Measuring and Control Technology and Instrumentations of Heilongjiang?Province，Harbin Uinversity?of Science and Technology， Harbin 150080， China）

Abstract：Aiming at the problem of severe degradation of fog weather image and low contrast， an improved algorithm is proposed?From the point of view of time?frequency analysis， the Fourier transform in the homomorphic filtering algorithm is replaced by the fast wavelet transform， and then the wavelet coefficients are processed by the improved filter in the transform domain to achieve the enhanced fog image purpose?The experimental results show that the improved algorithm can effectively correct the fog image illumination， keep the original information of the image is not lost， enhance the contrast of the image， and make the processed image more visible

Keywords：homomorphic filtering; wavelet transform; image enhancement; contrast

0引言

有霧天氣條件下，通過交通和公共場所攝像頭攝取的圖像，由于霧的影響，導致圖像的對比度降低，圖像的整體質量下降，影響了對遠處景物和人物信息的觀察和辨別[1]。降質圖像嚴重影響了戶外視頻及圖像采集設備的應用，這對城市交通、衛星監控等帶來了安全隱患，給相關人員的工作帶來的一定的阻礙。所以對霧天所獲取的降質圖像進行增強處理，提高圖像的可視度具有重要的現實意義。

對于圖像增強去霧的算法，國內外學者都做過大量的研究，常用的方法有直方圖均衡化算法，該算法簡單，但是由于霧而使圖像對比度降低與景物的遠近并非線性關系，所以該方法的效果并不理想，有時由于將景物的灰度值增強或減弱后反而會影響圖像的信息量[2-5]。同態濾波算法，該算法可以對光照不均的圖像進行校正，但由于處理是面向整幅圖像的，不可避免的去除一些有用信息[6-7]。小波變換算法[8]。Retinex算法，自適應能力差，而且在光照突變的區域容易產生光暈[9-11]。基于物理模型的方法，該方法對視頻采集的要求過于苛刻，算法復雜度高[12-13]。

為了簡化算法的復雜度，同時增強圖像的對比度，提出了一種改進的算法。由于小波變換在時域和頻域同時具有良好的局部特性，比傅立葉變換有明顯的優勢，因此本文采取小波變換代替傅立葉變換，從而達到快速去除霧對圖像的影響。

1算法的基本原理分析

1?1同態濾波的原理

同態濾波是一種把頻率過濾和灰度變換結合起來的圖像處理方法，它把圖像的照度反射模型作為頻域處理的基礎，通過對圖像的灰度范圍的調整，可以有效解決圖像上照度不均勻及動態范圍過大對圖像產生影響的問題，在不損失亮區細節信息的同時，有效增強暗區的細節信息[14]。

一般有霧天氣的圖像?f（x，y）由兩個分量表示：

f（x，y）=i（x，y）·r（x，y）（1）

其中：0

其中i（x，y）為照射分量，頻譜處于低頻區域，r（x，y）為反射分量，頻譜處于高頻區域，由于當一幅圖像從物理過程產生時，它的值與照度分量成正比，因此 ，反射分量的取值范圍為0

ln?f（x，y）=?ln?i（x，y）+?ln?r（x，y）（2）

上式表明，圖形亮度值的對數等于照射分量的對數值和反射分量的對數值的線性之和，是一個高低頻函數的線性的疊加。對（2）式進行傅立葉變換，將圖像從時域轉換到頻域：

F[?ln?f（x，y）]=F[?ln?i（x，y）+?ln?r（x，y）]（3）

F（u，v）=I（x，y）+R（x，y）（4）

其中F（u，v）代表?ln?f（x，y）的傅立葉變換，I（x，y）代表?ln?i（x，y）的傅立葉變換，R（x，y）代表?ln?r（x，y）的傅立葉變換。使用同態濾波傳遞函數H（u，v）進行濾波處理[15]有：

H（u，v）F（u，v）=H（u，v）I（x，y）+H（u，v）R（x，y）（5）

設S（u，v）=H（u，v）F（u，v），將濾波后的頻譜S（u，v）進行傅立葉逆變換，有：

F?-1[S（u，v）]=F?-1[H（u，v）F（u，v）]（6）

可寫成下式：

h?f（u，v）=h?i（x，y）+h?r（x，y）（7）

左右兩邊取指數運算得：

exp[h?f（u，v）]=?exp[h?i（x，y）+h?r（x，y）]=

exp[h?i（x，y）]·?exp[h?r（x，y）]（8）

g（x，y）=i?0（x，y）·r?0（x，y）（9）

其中i?0（x，y）為?exp[h?i（x，y）]的值，r?0（x，y）為?exp[h?r（x，y）]的值。

經典同態濾波的流程圖如圖1所示：

1?2小波變換的基本原理

小波變換是當前應用數學和工程學科中一個迅速發展的新領域，由于小波變換具有良好的時域局部特性，同時具有多尺度分析能力，并且可以對信號進行多分辨率的分析，所以在圖像處理領域應用廣泛。

由于數字圖像通常用二維信號描述，因此在對圖像進行分解時采用二維離散小波，根據Mallat快速分解算法[16]，一幅圖像?f（x，y）可表示成：

f（x，y）=∑nA?j-1?φ?n，j-1?（x，y）+∑?L-1?j=0?D?n，j?φ?n，j?（x，y）（10）

其中，設f（x，y）∈L?2（R*R），{V?j}，j∈Z是L?2（R）空間的一個多分辨率分析，φ?n，j-1?（x，y）是二維小波函數，φ?n，j?（x，y）代表二維尺度函數，∑nA?j-1?φ?n，j-1?（x，y）是圖像的低頻部分（?LL?），∑?L-1?j=0?D?n，j?φ?n，j?（x，y）表示圖像在水平（?LH?）、垂直（?HL?）和對角線（?HH?）方向的高頻部分。A?j-1?是低頻系數，又稱近似系數。D?n，j?為高頻系數，又稱細節系數。對LL部分，可以繼續分解[17]，二維圖像的三級分解塔形分解如圖2所示：

同一維的細節系數的頻率高于近似系數，高維的細節系數的頻率低于低維細節系數的頻率。這是因為，低一維的近似系數通過小波進行分解，分解的結果為某一維的細節系數，而高一維的小波系數又可以通過該維的小波分解得到。

2融合小波變換的同態濾波器設計

2?1同態濾波的濾波器的設計

一幅圖像中像素達到的動態范圍由照射分量來直接決定，而對比度是由圖像的反射分量決定，表示灰度急劇變化的部分，因此我們要選用合適的同態濾波傳遞函數?H（u，v），來達到對這些分量的理想控制[18]。

因為相對圖像細節信息來講，霧天圖像的信息主要集中在低頻區域，因此，壓縮f（x，y）的灰度范圍或在頻域上減弱I（x，y）的頻譜成分;同時，r（x，y）反應圖像細節，可以用對比增強的方法增強這一分量的對比度，即在頻域上加大R（x，y）的頻譜成分。對于受到有霧天氣影響的圖像，我們采用改進的二階高通濾波函數作為同態濾波的傳遞函數，其表達式如下：

H（u，v）=（H?H-H?L）{1-?exp[-c（D?2（u，v）/D?0?2）]}+H?L（11）

其中H?H和H?L表示為高頻成分增加的倍數以及低頻成分減少的倍數，滿足H?H>1且H?L<1;c為銳化系數并且H?L

2?2基于小波變換的同態濾波過程

在同態濾波的經典算法中，圖像的處理使用的是傅立葉變換，如圖1所示，由于圖像在頻域上的濾波是面向整幅圖像的，只能反映某個頻率成分包含在信號中的總強度，不可避免的去除一些有用的局部信息。造成這種時域局部化矛盾的原因在于：傅立葉變換所采用的三角函數系在時域上沒有任何局部性[ ?19??]。同態濾波經典算法也經常用在消除惡劣天氣對圖像的影響中，但是它在增強圖像的對比度上不是很理想。與傅里葉變換相比，具有多分辨率分析特點的小波變換是一種對于信號的時間-頻率分析方法，在時間域和頻率域都能很好的表征信號的局部特征。

在有霧天氣圖片的處理中，小波變換算法通過進行小波變換分解出低頻系數和高頻系數，由于霧天圖像的大部分能量集中在低頻區域，所以我們可以對近似系數和較高層的細節系數進行弱化處理，這樣可以弱化霧對圖像的影響。處于低層的細節系數代表包含的是霧天圖像細節信息，為了使所處理的圖像更加清晰，對比度有所增強，采取增強低層細節系數的操作，這樣可以使處理之后的圖像輪廓更加的突出。Matlab仿真實驗結果表明，該改進算法在去霧的效果上明顯優于經典算法。

基于小波變換的同態濾波流程圖如圖4所示：

3仿真實驗結果與分析

3?1評價指標

3?1?1標準差

標準差是反映圖像細節信息的指標，是對鄰域中對比度的度量，對比度越大，圖像的色彩更加的鮮明，灰度層次表現越豐富，表達式如下：

σ=∑M?i=1?∑N?j=1?（F（i，j）-ω）?2M·N（12）

其中，ω為平均值;M為圖像的總行數，N為圖像的總列數;F（i，j）為圖像i行j?列的像素值。

3?1?2均值

圖像的均值反映的是圖像的平均灰度范圍，均值越大，圖像亮度越大;反之，圖像的亮度越小。

3?1?3信息熵

圖像的平均信息量由信息熵來表示，信息熵是一個重要的圖像的質量評價指標，對于一個隨機事件?A來說，若它出現的概率是P（A），那么它包含的信息量的公式為[20-21]：

I（A）=?log?1P（A）

即I（A）=-?log??2P（A）（13）

在信息論中信源輸出是一個隨機變量，所有可能符號的集合{b?i}被定義為信源符號集?B?，P{b?i}為符號b?i的概率，因此一幅圖像的平均信息量的表達式為：

H=∑L?i=1?P（b?i）I（P?i）（14）

將I（P?i）帶入其中得：

H=-∑L?i=1?P（b?i）?log??2P（b?i）（15）

當同概率分布時，信息熵最大，即當P（b?0）=P（b?1）=??=P（b?255?）時?，信息熵取最大值，根據熵理論，圖像的信息熵越大，它所含的信息量就越大，圖像的細節信息也就越豐富。

3?2結果與分析

本實驗在Intel（R） Core（TM）2?2.GHz CPU，內存4GB，操作系統為Windows 7旗艦版，采用Matlab2012仿真實現。本文選取的霧天原圖來源于網絡，圖5所示為霧天圖像原圖，圖6為經過同態濾波算法處理后的圖像，圖7為經過改進算法處理之后的圖像。采取主客觀相結合的方法對處理后的圖像進行評價。

如上圖所示，霧天圖像原圖5整張圖片被霧所覆蓋，畫面模糊不清，對比度不強，不利于觀察;經過同態濾波算法處理后的圖像6，圖像表面的霧得到了一定的去除，圖像的整體效果得到增強，圖像的光照得到校正，但圖像偏暗，細節信息有一定程度的丟失;經過改進算法處理之后的圖像7，色彩更加的自然，圖像的邊緣和輪廓信息更加明顯，對比度明顯增強，車輛和路況信息相對更加清晰。

下面通過具體數據對圖像的處理效果進行客觀的分析，表1為原圖和處理后圖像的數據統計分析表（數據保留到小數點后兩位）。

通過表1可知，就均值而言，同態濾波算法與改進算法的均值都低于原圖像的值，這是由于霧在成像過程中所呈現的像素值較高，去霧處理后圖像均值一般都會有所下降;改進算法的標準差要高于原圖，說明圖像的對比度有所提高，圖像更具有可視性;并且改進算法的信息熵要略高于原圖及同態濾波算法，說明改進后的算法處理的圖像含有更多的信息量，細節信息也更加豐富。

4結論

本文針對有霧天氣對圖像的影響，提出了融合同態濾波和小波變換的圖像去霧算法。將傅立葉變換替換成快速小波變換，利用小波變換在時域和頻域都具有良好的局部特性特點，避免了傅立葉變換的不足。從主觀圖像的視覺效果及客觀的性能指標分析可知，改進算法增強了霧天圖像的對比度，使圖像具有更好的可視性，從均值、標準差、信息熵的綜合評價的分析中可以看出，改進算法具有一定的優勢。

參 考 文 獻：

[1]陳俊君，徐冰.霧霾天氣條件下的機器視覺圖像清晰化研究[J].計算機工程，2017：43（2）：280.

[2]AEDLA R， DWARAKISH G S， REDDY D V. Satellite Image Contrast Enhancement Algorithm Based on Plateau Histogram Equalization[C]//2014 IEEE Region 10 Symposium. 2014：213.

[3]SMITHA M L， SHEKAR B H. Illumimation Invariant Text Recoginition System Based On Contrast Limit Adaptive Histogram Equalization in Viseos /Images[C]// Proceedings of the Third International Symposium on Women in Computing and Informatics.ACM， 2015：22（2）：174.

[4]楊玲，甄志明，劉國紅.基于多尺度邊緣提取的薄霧圖像處理方法[J].哈爾濱理工大學學報，2014，19（5）：94.

[5]姜柏軍，鐘明霞 . 改進的直方圖均衡化算法在圖像增強中的應用[J]. 激光與紅外，2014，44（6）：702.

[6]JEAN?PHILIPPE Tarel， NICOLAS Hautiere， LAUENT Caraffa，etal. Vision Enhanc?ement in Homogeneous and Heter?ogeneous Fog[J]. IEEE Intelligent Transportation Systems Magazine， 2012，4（2）：6.

[7]范有臣，李迎春，韓意，等. 提升小波的同態濾波在圖像煙霧弱化中的應用[J].中國圖象圖形學報， 2012， 17（5）：635.

[8]周樹道，王敏，黃峰，等.基于亮度小波變換和顏色改善的彩色圖像去霧研究[J].哈爾濱理工大學學報，2011，16（4）：59.

[9]張雪峰，趙莉.基于改進Retinex的圖像增強算法[J].南京理工大學學報 ，2016，40 （1）：24.

[10]侯天峰，程和生，張燕.基于Retinex的視頻自適應增強算法[J].現代電子技術， 2015，38（17）：68.

[11]汪東芳，巨筱.基于改進Retinex的霧天圖像增強研究[J].激光雜志，2016，37（4）：58.

[12]劉海波，楊杰，吳正平，等.基于暗通道先驗和Retinex理論的快速單幅圖像去霧方法[J].自動化學報，2015，41（7）：1064.

[13]李校林，王屈橋，燕歷科.基于改進暗通道先驗模型的遙感圖像去霧算法[J].電視技術，2017.41（1）：14.

[14]ZENG F， WU Q， DU J. Foggy Image Enhancement Based on Filter Varible Multi?Scale Retinex[J]. Applied Mech?anics & Materials，2014，505/506：1041.

[15]陶澤明，裴玉龍，杜文剛.基于MATLAB的車輛圖像濾波[J].哈爾濱理工大學學報，2008，13（1）：18.

[16]MALLAT S. A Theory for Multiresolution Signal Decomposition：The Wavelet Repre?sentation[J].IEEE Transactions on Pattern Analysisand Machine Intelligence.1989：11（7）：674.

[17]何立暉，張健沛，王強.基于小波變換復合混沌系統的數字圖像水印算法[J].哈爾濱理工大學學報，2010，15（3）：15.

[18]孫慧賢，羅飛路，張玉華. 基于小波變換和同態濾波的內窺圖像增強算法[J]. 探測與控制學報，2008，30（5）：69.

[19]黃靜靜，陳文靜，蘇顯渝，等.小波變換在調制度測量輪廓術中的應用[J]. 光學學報，2016，36（7）：77.

[20]金佩芬，秦富貞.基于改進Retinex算法的紅外圖像增強處理[J].激光雜志，2016，37（7）：43.

[21]穆為磊，高建民，王昭，等.考慮人眼視覺特性的射線檢測數字圖像質量評價方法[J]. 西安交通大學學報，2013（7）： 91.