并聯PFC Boost變換器中的混沌控制研究
胡乃紅
(安徽水利水電職業技術學院,安徽 合肥 231603)
由于并聯PFC Boost變換器的系統參數在該電路長期使用過程中,因電路中某些因素改變導致參數變化,系統失穩,直至分叉及混沌現象出現,系統性能惡化[1-4]。為避免出現這種情況,要對這種失穩和混沌現象進行有效的抑制。因此尋找有效的抑制措施具有十分重要的意義和實際價值。目前針對失穩和混沌的控制方法中,斜坡補償是一種較好的方法,而且簡單有效,能明顯改善電路的電流紋波,增強電路的穩定性。
1 PFC變換器
假設每個PFC變換器模塊的參數完全一樣,每個PFC模塊同步工作。圖1(a)為單個PFC變換器的電路組成圖,它的微分方程為:

(1)
其中,x為狀態矢量,即x=[iL,vo]T,系數矩陣分別為:

(2)
圖1(b)為多級并聯PFC Boost 變換器的等效電路。每個PFC變換器模塊參數完全相同,包括L,Gd,Gs,L以及R。多級并聯的變換器有3種工作模式:臨界連續模式(BCM)、連續模式(CCM)和斷續模式(DCM)。連續模式和斷續模式一般用于小功率變換器,連續模式一般用于大功率和要求較高的場合[5-9]。其對應的微分方程為:
(3)
其中,x為狀態矢量,即x=[iL總,vo]T,對應的系數矩陣分別為:

(4)

2 多級PFC Boost電路工作的理論分析
對于多級PFC Boost變換器來說,工作過程中可以看成連接的直流變換器的序列。正斜率參考電流補償信號能夠很好地控制交叉及混沌,使其穩定工作;負斜率參考電流信號能夠使電路產生分叉直至混沌,降低穩定性[8-9]。圖2為并聯PFC Boost變換器每一級的電感電流工作波形:在開關管工作過程中,1個工作周期內,時鐘信號開始時GS導通,L中電流持續上升;當L中電流上升到補償電流時,GS斷開,L中電流持續下降。圖中m1、m2分別為:
(5)

圖2 電感L中的電流波形

圖3 加入斜坡補償的PFC Boost變換器工作波形

iCE=Δi0,IBC=Δi1
(6)
iCD=|-m′|*ΔDTs
(7)
iDE=m1*ΔDTs
(8)
iBD=|-m2|*ΔDTs
(9)
由式(6)、式(7)、式(8)、式(9)整理得:

(10)

(11)
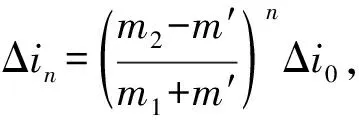

(12)
將m1,m2,m′代入得變換器穩定工作的臨界條件為:

(13)

(14)

(15)
可以計算出斜坡補償信號的幅度要求為:
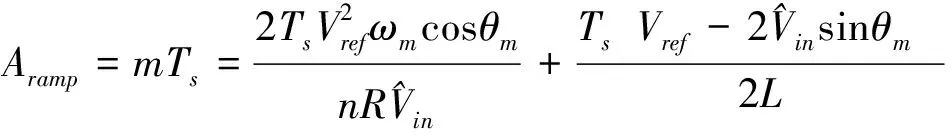
(16)
式(16)可近似表達為
(17)
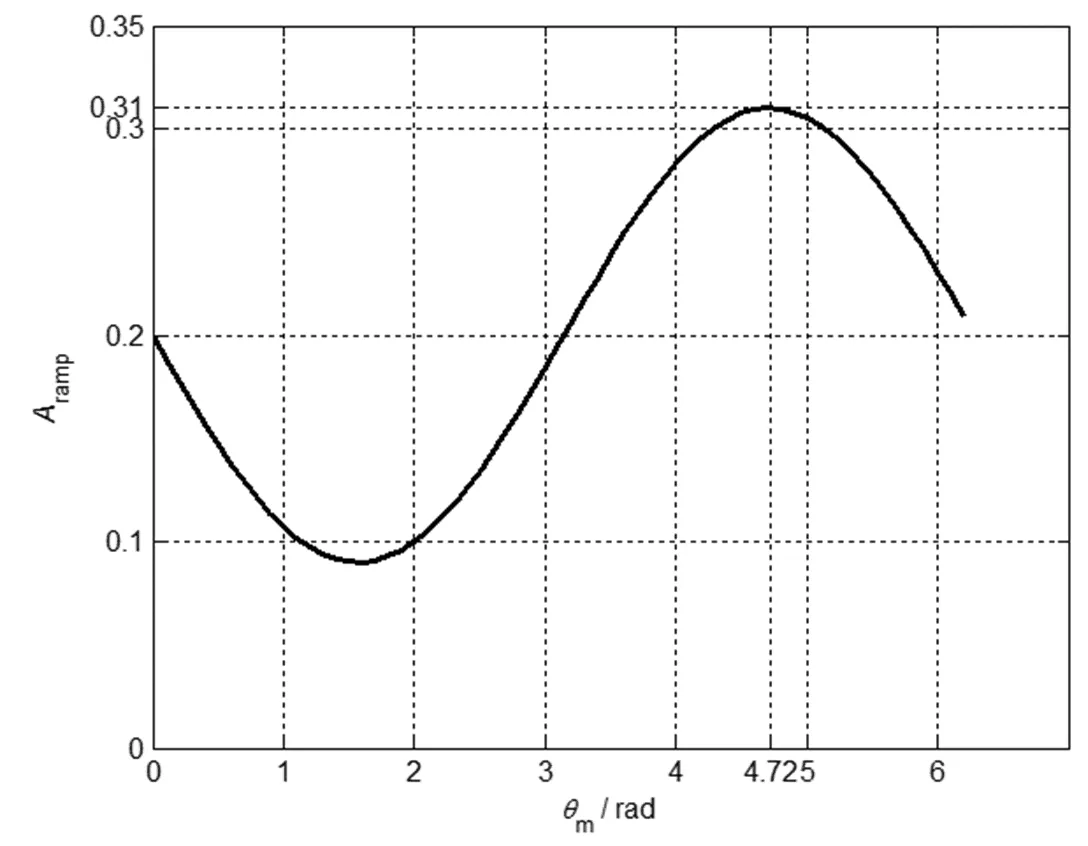
圖4 相位對應的斜坡補償幅度

3 斜坡補償后數值仿真結果
根據斜坡補償信號的幅度表達式(17),應用斜坡補償對圖1中電路不穩定性以及混沌進行控制,得到最佳的補償幅度為0.31,利用Matlab進行數值仿真,得到的電壓電流波形如圖5所示,根據輸出電壓、電感電流時域及頻閃采樣的數值仿真波形,可以認為電路工作于全局穩定的規則狀態。

圖5 恰當斜坡補償下的電路工作波形
4 結束語
并聯PFC Boost變換器電路在實踐中應用廣泛,但由于系統中某些參數受到影響而改變,導致電路將出現失穩甚至達到混沌狀態,使系統性能惡化。在實際的變換器電路設計中,希望該設計電路能穩定工作。

