基準轉換參數求解方法研究

葛露露， 顧和和

(1.安徽水利水電職業技術學院，安徽 合肥 231603; 2.中國礦業大學， 江蘇 徐州 221116)

不動產登記需要大量的不動產數據,這些數據由各個不動產部門提供,它們有自己的數據采集標準。通常采用最小二乘法[1]求解不同基準之間的轉換模型參數。但是,最小二乘法具有局限性,因此,考慮采用穩健估計的方法求解轉換模型的參數,并用實例驗證。

1 參數求解方法

1.1 最小二乘法(LS)[2]

該法是測繪行業最為常用的一種模型方法,其中高斯-馬爾科夫(G-M)模型最經典。在系數矩陣B中不含有誤差的前提下利用G-M模型求解,該模型沒有顧及系數陣中含有的誤差,僅考慮L中的偶然誤差,V為殘差向量,最小二乘原則:

VTPV=min

(1)

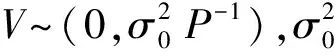
(r為多余觀測數)

(2)

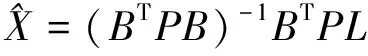
(3)

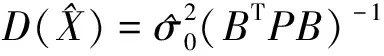
(4)

G-M模型簡單容易理解和掌握,但G-M模型求解參數沒有顧及可能含有粗差的情況, 只考慮了L中有偶然誤差,一旦含有粗差,求解的參數偏差較大,無抗差性[3]。

1.2 降權法

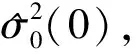
(5)

(6)

對其進行Fi檢驗:

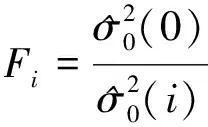
(7)

Fi服從F分布,其顯著水平為α,對應的自由度為r1,r2,即:

Fi～F1-α(r1,r2)

(8)

4參數模型的自由度為:r1=2n-4,r2=2(n-1)-4,n為參加計算的點的個數。

由于出現可靠數據低于3個時不能進行方差比值法檢驗,所以對特別明顯的粗差才直接剔除,不是非常明顯的粗差則降權處理,用不同的2個顯著水平不同作為區分不同程度同的粗差,令α1<α2,α1用來區分特別明顯的粗差,α2是用來能夠發現粗差的水平,位于α1與α2之間的數據可能是粗差:

(9)

其中，(v)代表的是迭代的次數,通過之前大量的實驗得出當α1=0.05,α2=0.35[5]時效果比較好。

1.3 降權最小二乘法

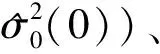
2 實 例

使用LS法和降權LS法,分別求解4參數模型參數,并對求解精度進行比較。表1是2套坐標系中點的坐標值, 1-8號點粗差未知的基準點,9、10號是不含粗差的檢核點。

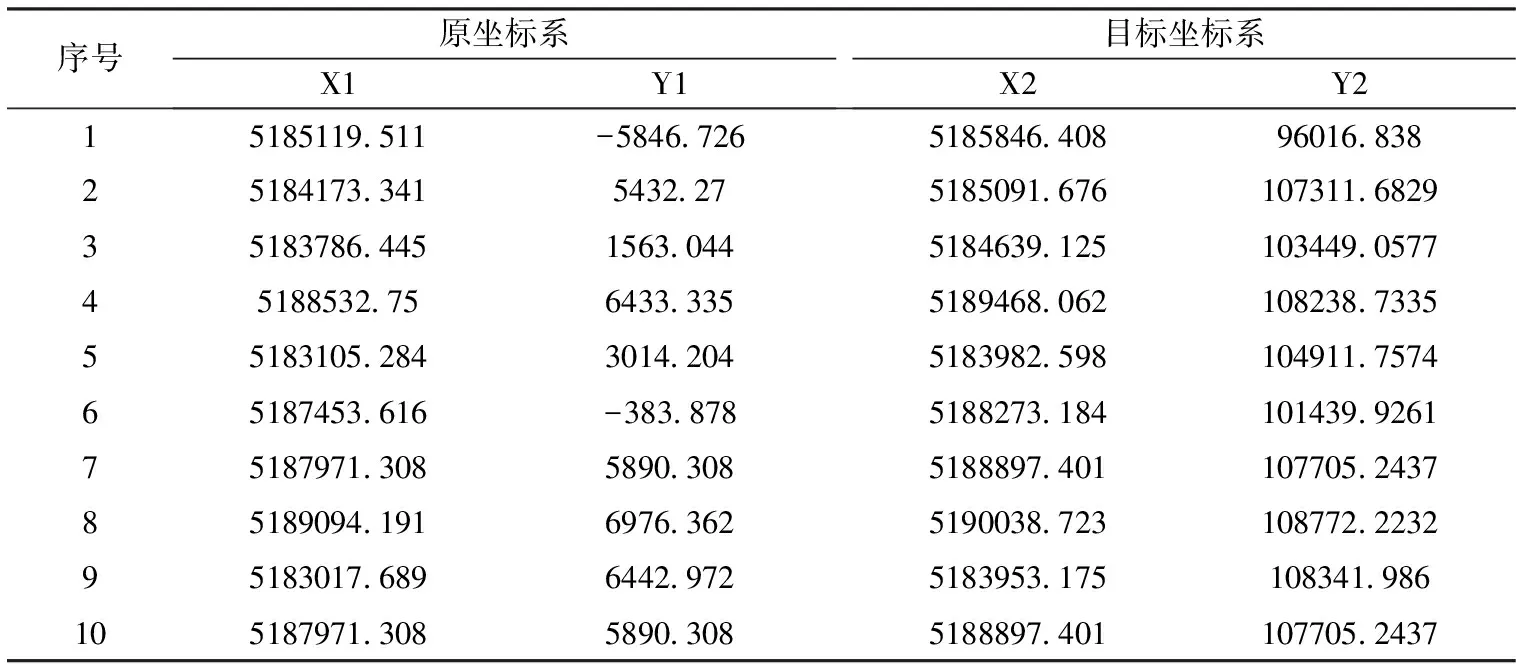
表1 2套坐標系的坐標

構建模型:

V=BX-L

求解縮放尺度κ、旋轉參數α、平移參數a、平移參數b及單位權方差,結果如表2所列。

表2 求解的參數及單位權

由表2可見,LS法的單位權方差的精度要低于降權LS法的單位權方差精度。利用求出的兩組參數進行坐標轉換,將原坐標系中的重合點(包括轉換基準點和檢核點)利用求出的轉換參數求解,用式(10)將目標坐標系中的坐標與求解的坐標進行相減,獲得坐標殘差值,再利用式(11)計算轉換點和檢核點的點位中誤差,如表3所列。

Δxi=Xi-xi,Δyi=Yi-yi

(10)

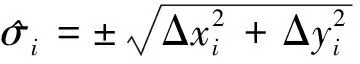
(11)

LS法受到粗差的影響,轉換點位誤差在0.7m-0.8m,降權LS法求解的點位精度在0.01m-0.03m。

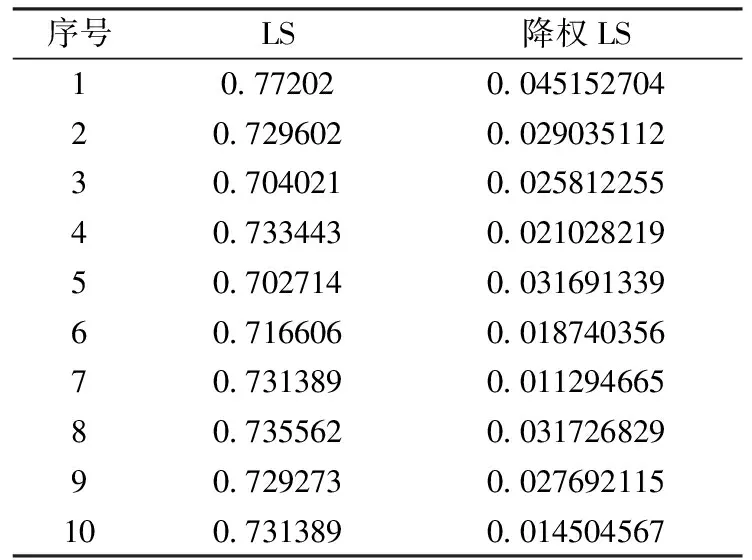
表3 各點的點位中誤差

據轉換基準點和檢核點的點位中誤差,計算內符合精度、外符合精度。假設有n1個基準轉換點(如果剔除點則要把剔除的點減掉),n2個檢核點,計算內、外符合精度公式如下:

(12)

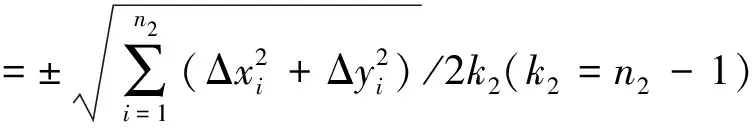
(13)

LS法求解的內、外符合精度為:55cm、 73cm,降權LS法求解的內、外符合精度為:1.2cm、2.2cm,其精度較LS法提高很多。

3 結束語

本文對求解坐標之間的轉換參數的求解方法進行了分析,并以4參數模型為例進行了演示,通過對4種不同參數求解方法的精度比較,可以發現如果數據中含有粗差LS法、TLS法不能得到可靠的參數解,但是采用降權方法可以得到較為可靠的參數解。本文僅以4參數模型為例,有可能存在一定的局限性,參數的求解精度還和選擇的模型、點的分布均勻情況等相關。