靜態電磁場計算中的廣義有限差分法應用

張翌 蘭州資源環境職業技術學院

有限差分是電磁場數值計算的一種重要方法，在很多的領域中都得到了廣泛的應用，比如電機溫度場的計算、磁場的計算等，對于一些網格變形或者復雜幾何的問題，如何有效的使用網格劃分的方式進行磁場計算是一項非常重要的難題。無網格法不同于其他的網格數值計算，無網格重要是通過節點信息的方式建立函數，然后根據節點之間的聯系建立鏈接，解決了傳統方法中存在的缺陷。無網格方法在近年來受到了廣泛關注，成為工程計算領域中的熱點話題。

1 研究背景

無網格法中，邊界型無網格是在邊界元法的發展中所得到的一種新的格式配置方法，在邊界元法的基礎上完善了問題維數的優勢，根據邊界配點得到邊界元法中較為復雜的計算方式。邊界型無網格方法在近幾年的發展中廣受歡迎，有多種不同的計算方法，每一種計算方法都有其自身獨特的功能，同時也或多或少的存在一些問題，比如此種方法限制了其應用范圍；區域性無網格正好彌補了邊界型方法中存在的缺陷，對各種微分方程的邊值計算具有一定的適用性特點，在工程計算領域中得到了廣泛的而應用。區域性無網格也有多種不同的計算方法，其中以廣義有限差分法為主，也就是本文重點介紹的內容，廣義有限差分法作為一種新興的區域性無網格計算方法，集合了多種功能，組合了控制方程中的導數與函數，解決了傳統有限差分法中存在的依賴性特點，同時，使用該方法所生成的稀疏陣能夠進行快速求解，在國內外的研究中都得到了廣泛的研究，特別是工程領域。自適應廣義有限差分法以進行自動配電，滿足一定的精度要求，還可以實現四階偏微分方程的邊值計算，并對其進行求解。對廣義有限差分法進行詳細的研究后，得到各種因素對廣義有限差分法帶來的數值結果影響。

2 廣義有限差分法基本概念

廣義有限差分法分步驟進行，在求解的區域內進行任意設置，找到與其距離相近的點，這個點就稱之為支持域，在這個支持域中有很多個點，將多個點的函數值分別在泰勒處展開。得到：

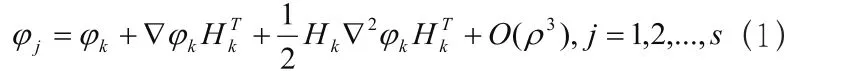
根據公式（1），得到：

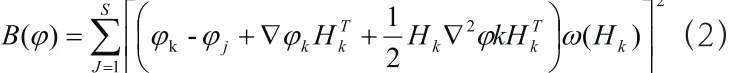
公式（2）表示殘差函數，根據最小二乘原理，將公式（2）中的相關元素進行求值，得到：

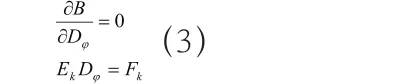
3 廣義有限差分法的計算過程

廣義有限差分法在構建線性方程的時候，可以使用泰勒和最小二乘相結合的方式進行構建，這種構建方式并不需要對插值函數進行計算，同時還可以有效的避免太過復雜的區域對網格帶來的計算阻礙。在實際的應用過程中，廣義有限差分法與其他的無網格計算方法相同，比較適用于偏微分方程的計算問題。既然可以計算偏微分的方程問題，也可以計算電磁場問題，其計算步驟為：

假設在該網格區域內有一個區域，用 表示，則靜態電磁場的數學模型為：

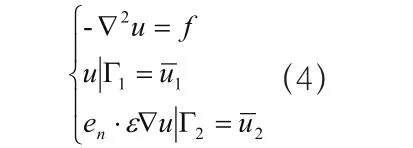
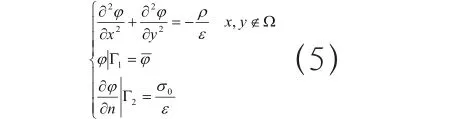
其靜態磁場數值計算公式為：

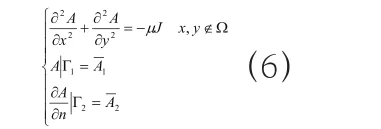
根據廣義有限差分法的相關理論知識，可以將電磁場的計算步驟進行以下總結：

在區域內進行隨機放點；然后根據泰勒公式構建矩陣；對于區域內多個節點形成代數方程。在進行離散的過程中，一定要注意，如果節點在區域內，需要盡可能的滿足條件，得到：

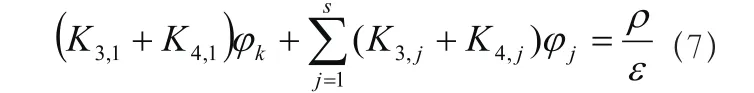
如果節點沒有在區域內，需要滿足條件：

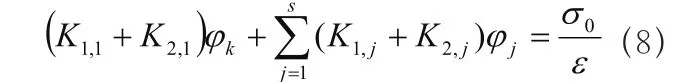
完成上述的計算后，計算方程組的值。

4 實例分析

為了更好的使用廣義有限差分法進行靜態電磁場的計算，需要不斷完善其計算方法，在處理一些較為復雜的問題時，傳統的有限差分法會對網格存在一定的依賴性，從而造成計算的結果存在較大的偏差。所以，為了更好地驗證廣義有限差分法的有效性，對比傳統的有限元方法與廣義有限差分法在模擬電位與磁場分布時的不同之處，將復雜求解域考慮其中，他對避雷針的電位分布進行模擬計算，并對計算的結果進行對比，以得到在計算問題中所存在的差異性。

在具體的實例中，如果沒有對其進行具體的說明，分布的方式均采用絕對誤差的方式進行計算，采用四階泰勒展開式的方式對算例的數值逼近進行計算，數值之間的相對誤差為：

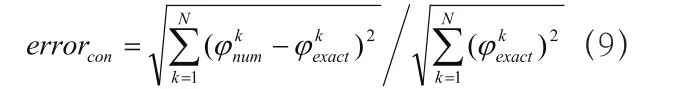
對存在金屬電磁場的數值進行計算，比如有一個接地的金屬槽，頂蓋與底面的電位分別為與0，能夠滿足區域內的方程條件，其求解的區域方程為：

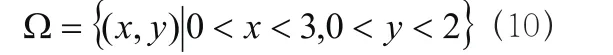
解析公式為：

在求解的區域中選擇若干個節點進行計算，每一個節點中所選擇讓點作為支撐域，并使用廣義有限差分法進行配電，從而得到有限元的網格解剖結果。根據計算公式，能夠得到廣義有限差分法求解的金屬槽電位，同時還能夠得到磁場分布的最終結果。通過不同的計算方式，能夠得到不同的電位分布效果，說明不管使用哪一種方式都能夠得到較為可靠的計算結果。使用廣義有限差分法能夠得到更為準確的精度，降低相對誤差，而有限元方法的計算精度較差些，說明使用廣義有限差分法還是具有十分明顯的優勢。

5 結束語

綜上所述，在靜態電磁場的計算中將廣義有限差分法應用其中，能夠在非常復雜的電磁場環境中得到非常精確的計算效果，其非線性處理的問題需要作進一步的研究。