非球面折反射全景成像系統設計

（長春理工大學 光電工程學院，長春 130022）

近年來，隨著機器視覺、VR等應用領域的日益發展，在生活中需要采集的圖像信息也越來越豐富，而傳統相機的成像視場就存在了一定的局限性，為了解決傳統相機視場角狹窄的問題，360°全景相機應運而生［1］。全景成像技術從80年代起，就受到越來越多的國內外研究學者的關注，他們對此作了大量的工作與研究，并且也取得了一定的研究成果。在視頻監控和安防領域中，日本Sony公司的專利Desktop Model RPU-C251中，就引入了折反射全景成像技術，Conroy L等人研究了使用兩個反射鏡與相機配合組成的立體視覺系統［2］。浙江大學課題組對折反射相機模型進行了研究，并提出全景凝視成像的方法，獲得了成像視場角為180°的圖像［3］。Christopher Mei等人研究了單視點全向平面柵格的全景成像相機的標定方法［4］。北京理工大學課題組通過設計雙曲面反射鏡實現了全景成像［5］。哈爾濱工業大學的研究小組對一個帶有凹面反射鏡的圓柱形成像系統進行了設計與分析［6］。

目前，全景成像的實現方式主要有以下四種：多圖像拼接技術，魚眼鏡頭，環視透鏡系統，折反式光學系統［7］。折反式全景相機是近幾年發展起來的一種新的環型全景成像形式，與旋轉式掃描相機、多圖像拼接相機和魚眼相機相比，在很多方面都具備顯著優勢：尺寸小、結構靈活簡單、成本低廉、實時性好［8-9］。

折反射全景相機主要由三部分組成，即曲面反射鏡、成像透鏡組和CCD相機。它與魚眼鏡頭折射的方式不同，魚眼鏡頭是通過折射來壓縮視場角，折反射相機是利用曲面反射鏡對水平方向入射的光線進行收集與壓縮，并轉入到后面的成像系統中，進而獲得360°環視全景成像的效果。折反射全景成像系統分為單視點和非單視點兩類，單視點成像表示進入系統時的入射光線的延長線有唯一交點，它符合針孔相機模型，不然即為非單視點成像。跟非單視點系統相比，單視點系統的物像映射關系比較容易，根據單視點成像的約束條件可以計算出鏡面的特定曲面面型，并且部分計算機視覺理論和算法均適用該類成像系統。而非單視點成像的面型求解就比較麻煩，它需要用不同的投影方法去獲得，最后再用高階方程的擬合求解鏡面的曲面方程［4］。

為了實現視場清晰的折反射全景成像系統設計，不僅要對球差、彗差、色差等影響成像質量的像差進行校正以外，還要對系統產生的畸變進行特殊的控制。在折反式系統中，反射鏡面型的設計就對畸變的控制起到了關鍵性的作用。因此，利用單視點折反射全景成像的理論思想，設計了一款高階非球面反射鏡和常規成像透鏡組相機相結合的系統，有效控制了畸變對鏡頭的影響。系統的視場角為360°×（-50°～15°），畸變量在50%以下。

1 折反射全景成像系統的設計

1.1 折反射全景成像系統尺寸的計算

系統的外形尺寸主要由反射鏡離攝像頭的距離h和反射鏡的口徑D決定，如圖1所示，曲面反射鏡一般是以光軸旋轉對稱的，像素平面為長方形，取像素平面的短邊所在的剖面進行分析。dmin是像素平面短邊上的有效像素點到圖像中心點的最短距離，f為透鏡的焦距，通過反射鏡壓縮后的視場角為θ：

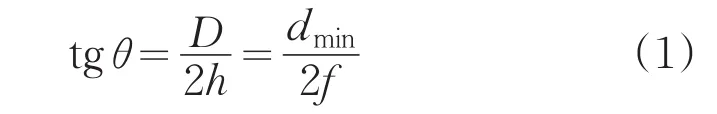
式（1）表示了折反射全景系統中的系統尺寸、CCD尺寸和視場角之間的關系，設計系統時根據應用要求選取合適的攝像頭和視場角，標定出dmin和透鏡的焦距f，并確定合理的反射鏡口徑D和反射鏡到攝像頭的距離h。

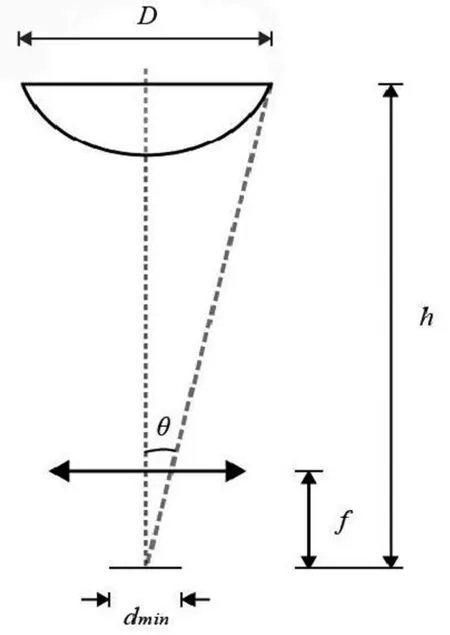
圖1 折反射全景成像系統的尺寸關系

1.2 單視點成像的幾何分析

本節以單視點結構為約束進行討論，以雙曲面反射鏡為例，推導了滿足單視點約束并且采用雙曲面反射鏡的系統結構參數。符合單視點約束的系統反射鏡都具有兩個焦點F1點和F2點，一個位于反射鏡面的內側F1處，另一個則在反射鏡外側F2處，兩個焦點的光學性質就是入射光線經過F1，反射光線經過F2，如圖2所示。全景相機的投影中心C點與F2相重合，則光線穿過C點，投影在探測器上。單視點折反射全景系統由C點和F1兩個點共同約束，可以建立類似傳統成像的透視投影模型，進而計算出系統的設計參數。

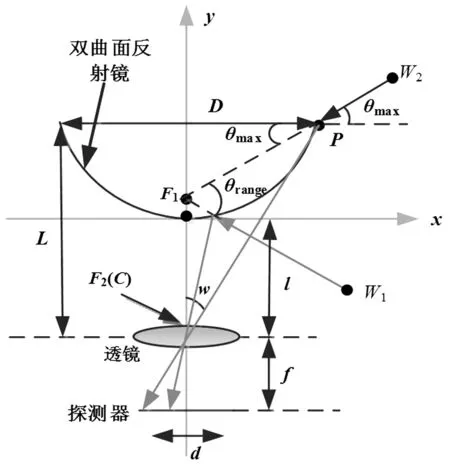
圖2 單視點折反射全景成像系統結構圖

圖中l為反射鏡頂點O與投影中心C點之間的距離，L定義為反射鏡與透鏡組的距離約束，e代表圓錐曲線離心率。該坐標系下的雙曲線可表示為：

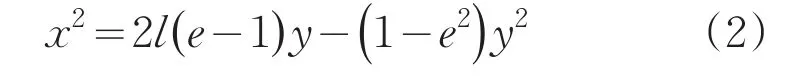
由三角相似關系可以得出：

其中，D為反射鏡口徑，f為反射鏡的焦距，d為探測器尺寸。

最大俯角θmax的正切值為：

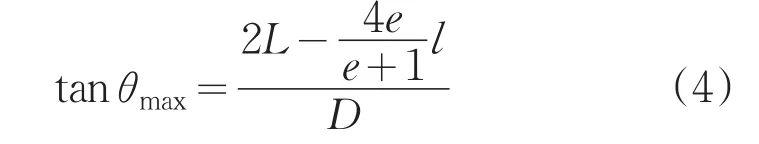
由于P點在雙曲線上滿足（2）式，在已知D和f的情況下，L可以直接由（3）式解出，（3）和（4）式聯合得到（5）式，l和e可以由（1）和（5）聯立解出。

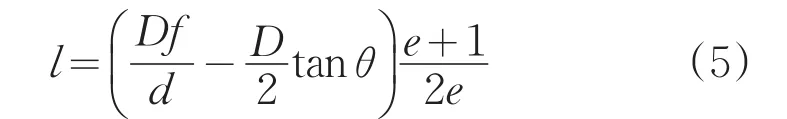
利用求得的參數值就可以設計出滿足特定的像面尺寸和視場角的折反射全景成像的系統結構。在單視點約束的結構下，通過優化折射透鏡組的參數便可以實現全視場的清晰成像。

2 實驗及結果

基于以上系統參數的計算方法，本文設計了一套高階非球面折反射全景成像的光學系統。整個鏡頭可以滿足大于800萬像素的分辨率，鏡頭焦距f為0.7mm，水平全視場角達到360°，俯角-50°，仰角15°，其光學總長度小于45mm，光學的最大口徑小于25mm。

系統中采用了高階非球面作為反射鏡，大大降低了系統鏡片的數量，透鏡組采用球面設計，可以通過優化系統來矯正各種像差，并且為了更好地矯正色差和球差，在透鏡組中引入兩組雙膠合透鏡。在折反射系統中，對于成像分析的需要，非球面透鏡的引入可以提高成像質量，因此反射鏡的面型就起到了關鍵性的作用，以下是高階非球面的數學表達式：

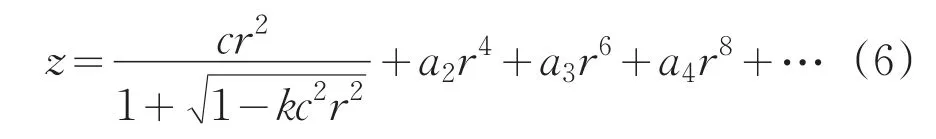
通過最小二乘法擬合出實驗設計結果的高階非球面的各項系數如表1所示。

表1 高階非球面方程系數

根據參數的選取和優化，利用Zemax軟件進行光線追跡得到的系統光路圖和成像質量分析如圖3-圖6所示。

其中，從圖4可知探測器的頻率在120p/mm處以內的MTF均在0.2范圍內，從而可以滿足該系統成像的要求。從圖6的點列圖可以看出該鏡頭的各視場的彌散斑半徑均在8mm以內，可以初步判斷系統處于衍射極限狀態。以上的成像性能結果都可以證明該系統具有較好的成像質量，符合設計的要求。

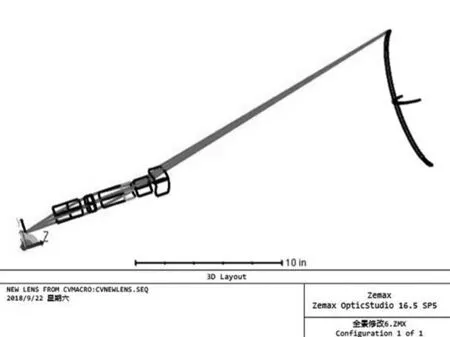
圖3 系統的光路圖

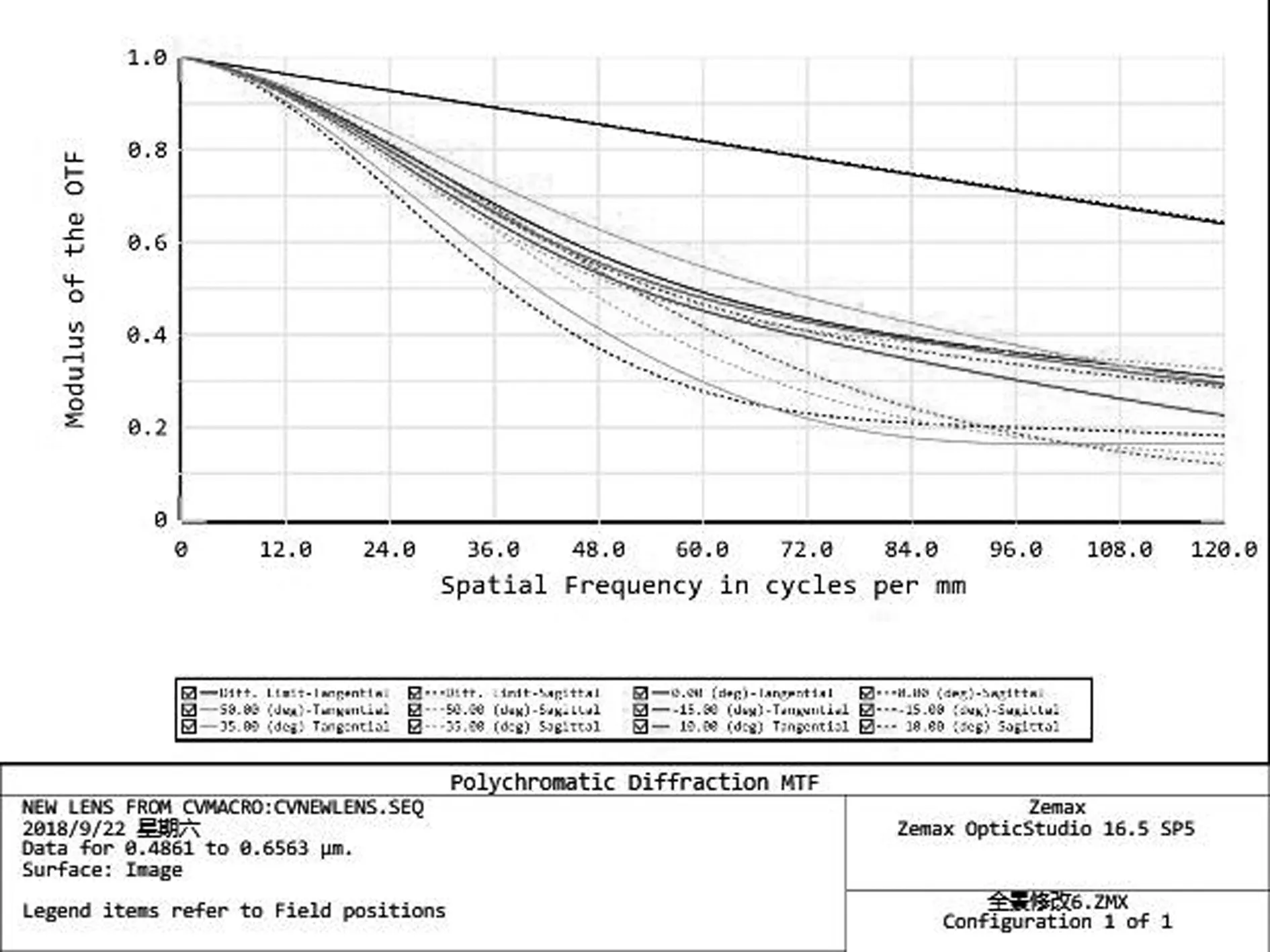
圖4 調制傳遞函數（MTF）曲線圖

圖5 場曲和畸變圖

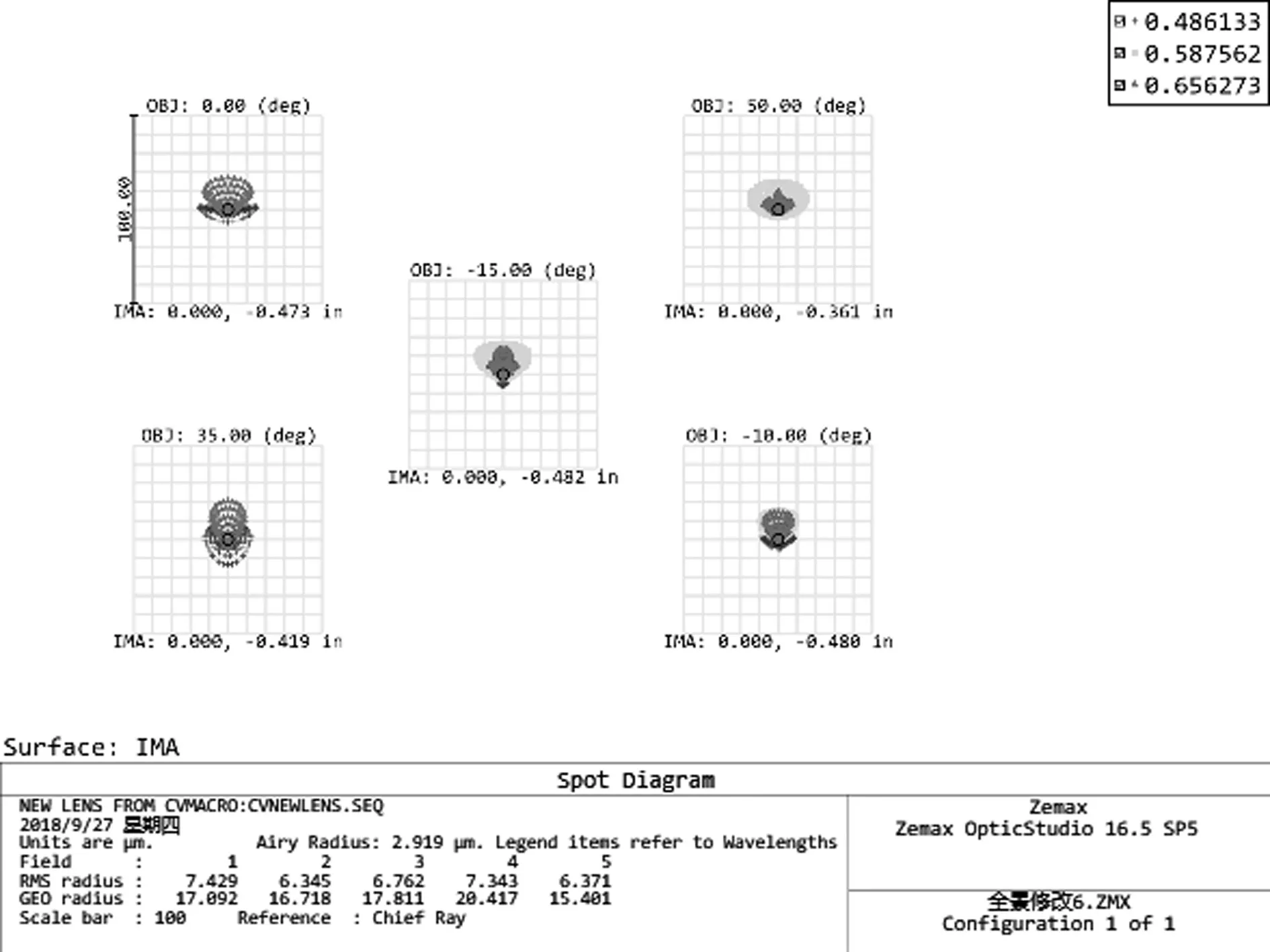
圖6 點列圖

3 結論

本文除了對全景成像技術做了簡單的概述外，還對單視點折反射式的全景成像系統進行了詳細介紹與理論分析。通過反射鏡與成像透鏡組的相結合，有效矯正了系統的像差，同時通過設計一款全新的高階非球面，解決了折反式全景鏡頭對于畸變的控制問題。系統的視場角達到了360°×（-50°～15°），探測器的頻率在120p/mm處以內的MTF均在0.2范圍內。該系統在安防監控，智能家居以及車載影像領域均具有廣闊的應用前景。