一種基于倒排索引的頻繁項集挖掘方法

（長春理工大學 計算機科學技術學院，長春 130022）

大數據時代的到來，數據呈爆炸式增長，為了能夠從大量的數據中挖掘出有價值的信息，研究關聯規則得到了高度的重視，關聯規則挖掘過程一般包括兩步：（1）頻繁項集的識別（2）從頻繁項集中挖掘隱含關聯規則［1］。其中頻繁項集的識別是整個挖掘過程的主要部分，頻繁項集的規模也決定了數據挖掘性能。

目前，已有眾多學者針對頻繁項集挖掘的經典算法進行改進，他們分別從“事物：項集合”和“項目：事務集合”兩種方式展開研究，前者被稱為“水平數據格式”，后者被稱為“垂直數據格式”。文獻［2］利用了二維數組的結構來對算法進行了改進，大大減少了輸入輸出操作，使查找速度得到提高，但隨著數據庫中數據量不斷增大，導致了數據庫中的事務無法全部存入數組當中。文獻［3］提出的十字鏈表和二維數組相結合的方法實現了頻繁項集挖掘，但由于十字鏈表是靜態的，不能隨著挖掘過程的進行而隨時壓縮鏈表，因此增大了內存開銷。針對上述算法的問題，在二維數組的基礎上引入倒排索引結構，提出了一種基于倒排索引和二維數組的頻繁項集挖掘算法。

1 基于倒排索引和二維數組的頻繁項集挖掘

1.1 倒排索引表示事務數據庫

倒排索引［4-5］（Inverted Index），也稱為反向索引，是一種直接通過屬性值來確定該屬性所在記錄位置的索引方法，包括詞項詞典和倒排記錄表兩個部分。倒排索引是信息檢索系統中最常用的數據結構，倒排索引表是由一組包含屬性值和屬性所在地址的記錄所形成的二維表，其存儲結構對檢索的效率和效果起著至關重要的作用。倒排索引結構如圖1所示。

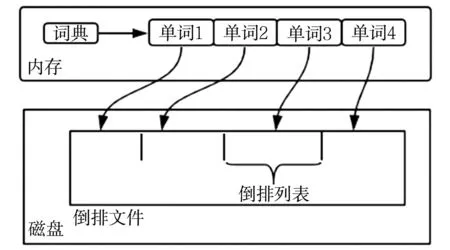
圖1 倒排索引結構

為了提高頻繁項集的挖掘效率，引入倒排索引技術，獲取其對應的事務編號Tid，并按Tid對應事務的項目長度進行分組，構建倒排索引。其中倒排索引由兩部分組成：第一部分是頻繁項目，其內容是頻繁項目頭節點；第二部分是倒排索引節點，由項目長度和事務Tid列表組成，對Tid按照事務長度列表進行分塊保存。對于包含N個項目的候選項集，采用倒排索引技術，每個候選項集只需掃描長度為N的頭節點表，并取出頭節點表中事務集合，這將大大提升掃描數據庫效率，從而提高頻繁項集挖掘的效率。

假設事務數據庫D共有6條事務，事務中的項目用I1，I2，I3，I4，I5，I6表示，每條事務都按字典順序排序，如表1所示。事務數據庫D對應的倒排索引如圖2所示，通過將項目的倒排索引轉換為列向量，并用“與”運算得到支持度，最后刪除小于支持度的頻繁項集。

表1 原始事務數據庫D

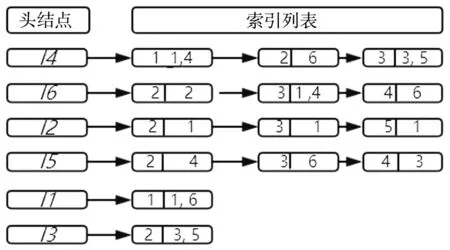
圖2 事務數據庫D對應的倒排索引

1.2 基于二維數組的候選k項集生成方法

首先，定義頻繁項集Lk，候選項集CK。將（k-1）項頻繁項集分為兩部分存儲到二維數組，記二維數組為Ak。將頻繁（k-1）項集的前（k-2）項集存儲到Ak的第0列，第（k-1）項集存儲到Ak的第1列，分組編號存儲到Ak的第2列，有效標識位存儲到Ak的第3列，其中1表示該項集可以和其他項集鏈接，0表示不可以鏈接。例如，頻繁3項集L3={{I1，I4，I6}，{I2，I3，I4}，{I4，I5，I6}}，它在二維數組Ak中的存儲形式如表2所示。

表2 頻繁3項集L3的二維數組

在存入二維數組Ak的過程中把頻繁（k-1）項集分組，由于Apriori算法［6］在執行連接生成頻繁K項集Lk+1的過程中，需要從Lk中找到兩個項集與前k-1項集均相同的項集，才可以連接，因此分組規則是把與第0列相同的頻繁項集分成一組；根據表2可知，頻繁3項集L3應該分成三組，第0行的{I1，I4，I6}分在第1組，第1行的{I2，I3，I4}分在第2組，第2行的{I4，I5，I6}分在第3組。由于兩個頻繁（k-1）項集鏈接生成候選項集Ck時，必須滿足前k-2項相同，第k-1項不同。根據鏈接條件，三組項集均無法與其他項集進行鏈接，所以第3列的有效標識位均為0。在生成候選k項集Ck時按照分組來進行，因為分組后的頻繁項集正好滿足了鏈接條件，不僅能生成所有的候選k項集，而且不會產生多余的候選k項集。

2 實例分析

下面以部分實驗數據為例說明挖掘頻繁項集的過程：

掃描數據庫，生成倒排索引。在生成倒排索引前首先根據項目編號得到對應的Tid值，再按照每個項目的Tid值個數進行分組，最后生成每個項目和Tid值的倒排索引。如圖2所示。

再次掃描數據庫，獲得頻繁1項集L1={I1，I2，I3，I4，I5，I6}，然后將頻繁1項集存入二維數組中，當存入二維數組時，需要遵循一定的規則，其中二維數組有四列，每列數據都有不同的意義，以頻繁1項集為例，第0列存儲前k-1項頻繁項集，因為頻繁1項集不存在前k-1項頻繁項集，所以第0列用空表示，第1列存儲第k項集，第2列存儲在第0列基礎上的分組編號，第3列代表各項集間是否可以鏈接，可以鏈接記為1，否則記為0。所以頻繁1項集對應存儲的二維數組如表3所示。

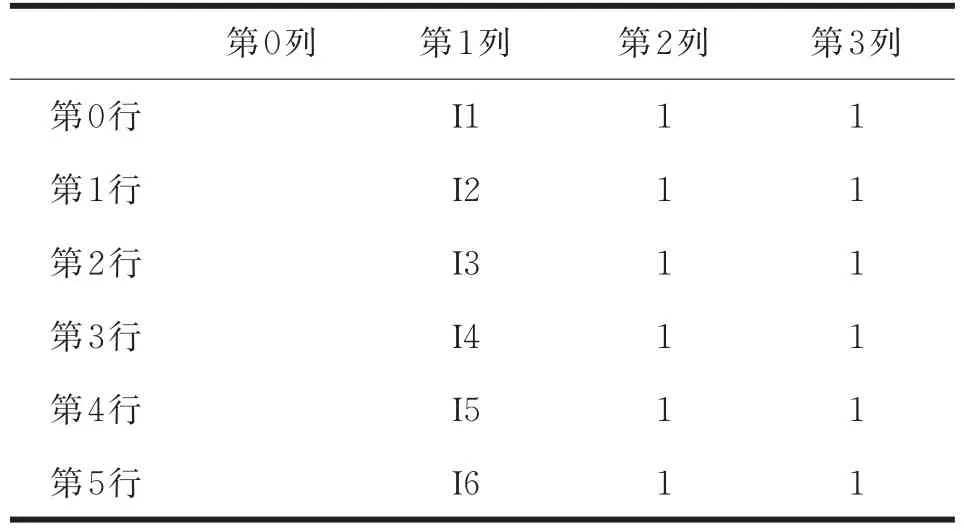
表3 頻繁1項集的二維數組

接下來生成頻繁2項集，由于所有頻繁1項集的第0列相同，且標志位均為1，因此直接鏈接生成候選頻繁 2 項集 C2={I1I2，I1I3，I1I4，I1I5，I1I6，I2I3，I2I4，I2I5，I2I6，I3I4，I3I5，I3I6，I4I5，I4I6，I5I6}，再通過上述的倒排索引技術計算支持度來篩選頻繁2項集。支持度計算以I1I4為例，I1的倒排索引是（1，6），相應的列向量R1=（1，0，0，0，0，1）T，I4的倒排索引是（1，3，4，5，6），相應的列向量R2=（1，0，1，1，1，1）T，計算R1&R2=（1，0，0，0，0，1）T，R1&R2結果中1的個數就是支持度，綜上所述可知I1I4的支持度是2，假設實驗設定最小支持度為2，因為I1I4的支持度等于2，所以I1I4為頻繁項集，依次計算得到頻繁2項集L2={I1I4，I1I6，I2I3，I2I4，I3I4，I4I5，I4I6，I5I6}。

利用上述方法生成頻繁3項集L3={{I1I4I6}，{I2I3I4}，{I4I5I6}}。

接下來計算頻繁4項集，根據性質，頻繁k項集若能產生頻繁（k+1）項集，那么頻繁k項集中項集個數肯定大于k。由于L3的個數小于4，因此不能生成頻繁4項集，算法結束。

3 實驗結果及分析

為了驗證算法的性能，分別在以下兩方面與文獻［2］、文獻［3］中的算法做了對比：一是最小支持度閾值不變，數據集規模不斷增加的情況（如圖3所示）；二是數據集大小一定，支持度不斷增加的情況（如圖4所示）分別得出實驗結果。

根據圖3所示，當最小支持度閾值不變而數據集不斷增加時，在數據集未達到25萬時，算法ALN的運行時間較短；當數據集超過25萬之后，文中算法的運行時間明顯少于Apriori-BR和ALN兩種算法，更適用于大數據的頻繁項集挖掘。

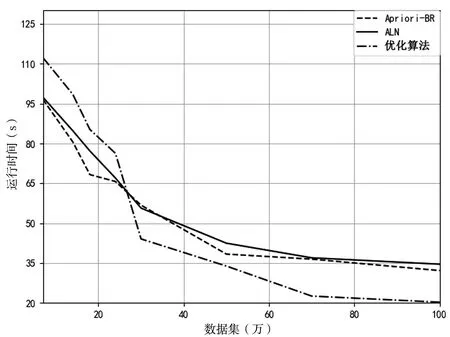
圖3 不同數據集下的運行時間結果

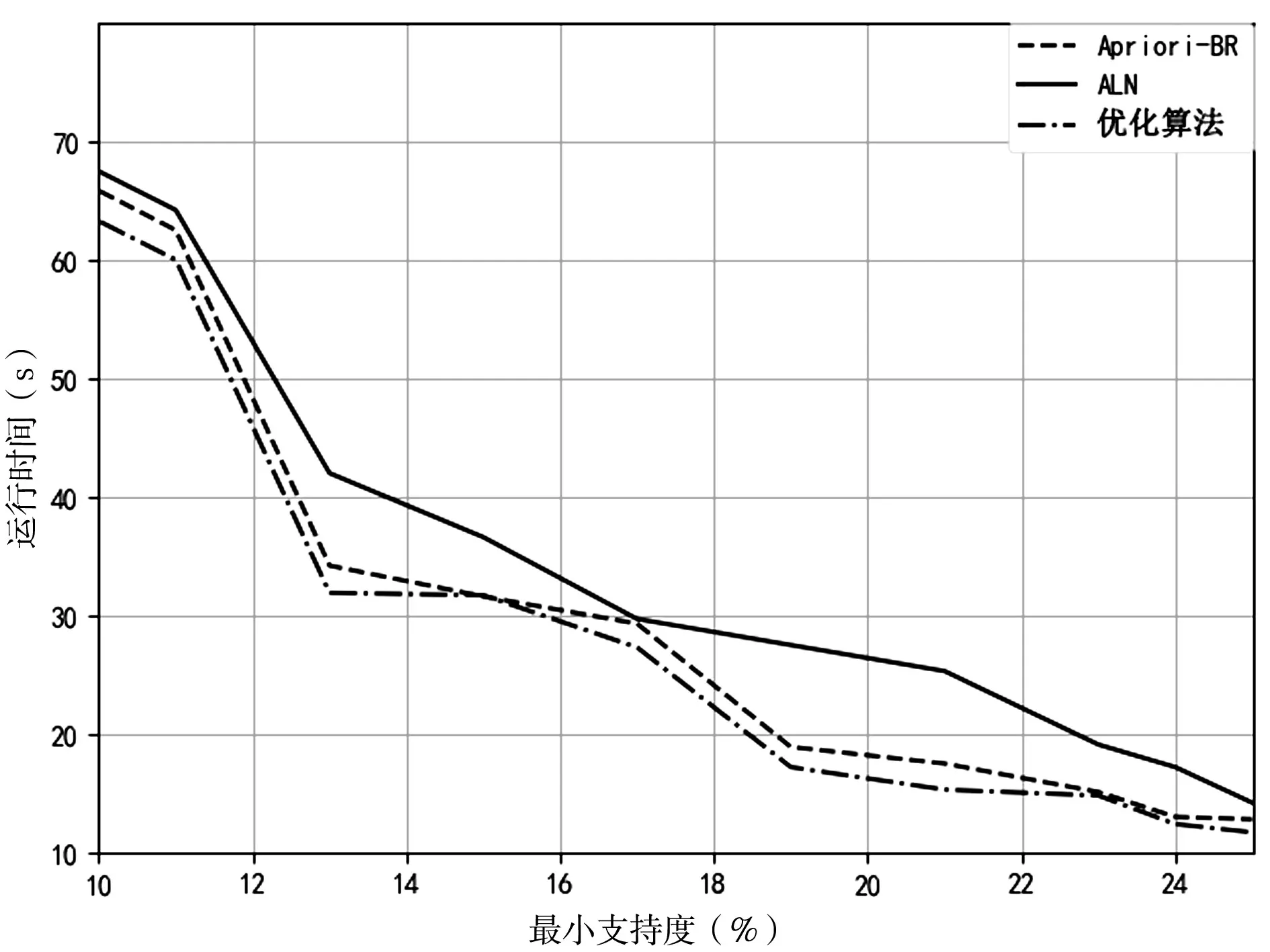
圖4 不同最小支持度下的運行時間結果

根據圖4所示，在原始數據集不變，最小支持度閾值改變時，文中提出的算法比Apriori-BR和ALN生成頻繁項集的系統運行時間短，故比其他兩種算法更高效。

4 結束語

通過對文獻［2］和文獻［3］算法的改進與結合，提出基于倒排索引和二維數組的頻繁項集挖掘算法。雖然該算法需要掃描兩次數據庫，但在數據集較大的時候，倒排索引技術大大提高了檢索效率，運行時間也相對較少。在計算支持度時無需掃描數據庫，并且通過標志位約束減少候選項集的生成數量，從而提高了候選項集的連接效率以及內存利用率。