基于協同過濾算法的推薦系統設計

□邵 娜

隨著互聯網的迅速普及，大量的信息充斥著人們的生活，這種現象稱為信息超載。面對這一現象，推薦系統應運而生。推薦系統結合推薦算法，通過分析數據庫中記錄的興趣愛好，進行個性化計算，由系統分析得到推薦信息，引領用戶發現自己真實需要的物品信息。

一、協同過濾的推薦算法

本系統設計假定用戶與商品評價之間是最簡單的線性關系，我們將基于這種最簡單的線性關系來敘述數據挖掘是如何計算參數的。當要處理更復雜的關系時，需要做的就是替換這種關系，但模型及算法步驟是很相似的。

(一)線性回歸。假定有一組數據記作xi,其中i=1,2,…n這是定義域，值域也就是輸出yi,i=1,2,…n，yi=theta0+theta1*xi，這就是假定的線性關系。數據挖掘的一般過程如下。

1.觀測數據。進行統計假設，可以假設數據近似服從線性關系y=theta0+theta1*x,同時這個數學表達也就是我們的目標函數。

2.建立代價函數。假設后要建立標準，看假設與實際情況相差如何，利用常用的代價函數最小二乘法以求出最優參數：J=sum(theta0-theta1*x-yi)2/n。將這個表達式記作J，要求的就是使J達到最小的theta=[theta0;theta1]。

3.求解代價函數的梯度。這是一個具有凸性的函數。利用凸優化的方法求出全局最優解。其核心部分就是求解代價函數的梯度，這里我們對theta進行求偏導，以得出梯度，

J'=X*(X*theta-y)/m。

4.梯度下降法。給定theta的初值，我們計算代價函數在每個點的梯度，讓參數沿梯度反方向移動一個很小的值，然后再重新計算梯度，直到算法收斂，這就是梯度下降法。用該方法得到的線性回歸結果。其中核心代碼在MATLAB中如下：

for r=1:num_iters

theta=theta-alpha*X'*(X*theta-y)/m;

Theta(:,r)=theta;

end

(二)協同過濾。協同過濾算法架構較為復雜，但具體到每一步其實很簡單，幾乎和線性回歸一樣。本文將使用的算法是共軛梯度下降法。核心步驟就是計算代價函數的梯度，這一步獨立于算法，是算法的輸出部分。

X=x-alphasumTj-y*Tj+lambda*x

Tj=Tj-alpha(sumTj-y*x+lambda*Tj)

步驟如下：第一，初始化x和theta，這個初始化是隨機的，一般用高斯函數來產生。注意隨機不代表隨意，如果胡亂取值，是不會得到好的結果的，事實上收斂速度和你取的初值是有關聯的。第二，用梯度下降法來計算X和theta，方法是固定X用公式f求theta，固定theta，用公式求X。核心代碼如下：J=(X*Theta'-Y).*R;X_grad=J*Theta+lambda*X;Theta_grad=J'*X+lambda*Theta;J=J(:)'*J(:)/2+(Theta(:)'*Theta(:)+X(:)'*X(:))*lambda/2。第三，用共軛梯度下降法反復迭代直到收斂，得到想要的數據關系。

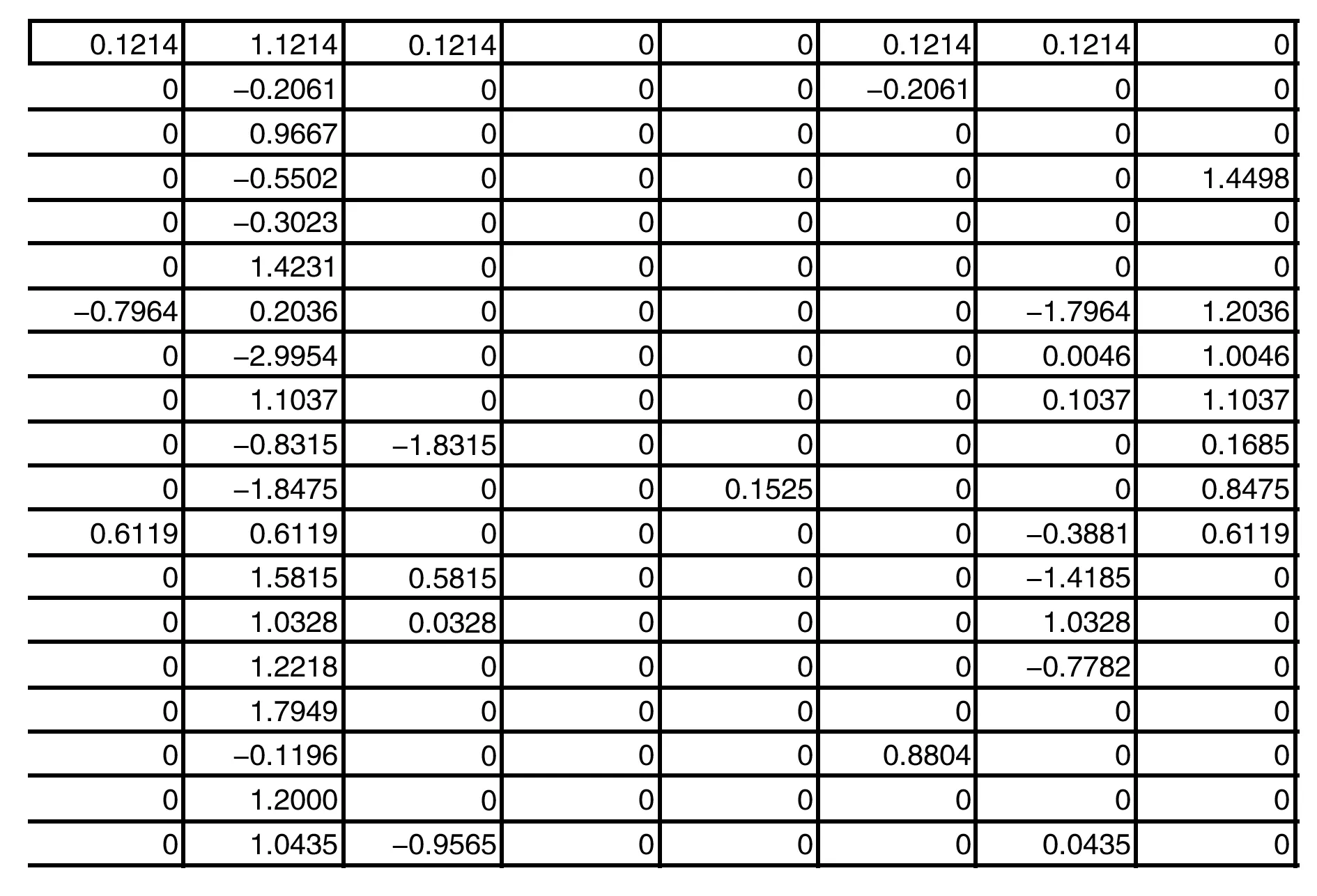
圖1 正則化后的數據

(三)共軛梯度下降算法。首先是數據需要進行中心化和單位化。比如Y=[5 5 3; 3 2 1; 0 1 3]，中心化后為[2. 33 2.33 0.667 ; 0.333 -0.667 -1.333; -2.667 -1.667 0.667]，然后進行單位化，這個在計算過程中特別重要，特別是對參數lambda的影響。關于共軛梯度下降法需要注意兩個關鍵點，一是收斂條件，選取的是Wolfe-Powell條件。這個條件講的是，當找到梯度之后，沿著這個梯度方向移動最適合。二是共軛梯度的計算。采用的是Polack-Ribiere共軛梯度法。共軛梯度法并沒有計算函數的二次導數，即Hessian矩陣，而是將Hessian矩陣與數據矩陣的乘積看成一個整體進行估計。

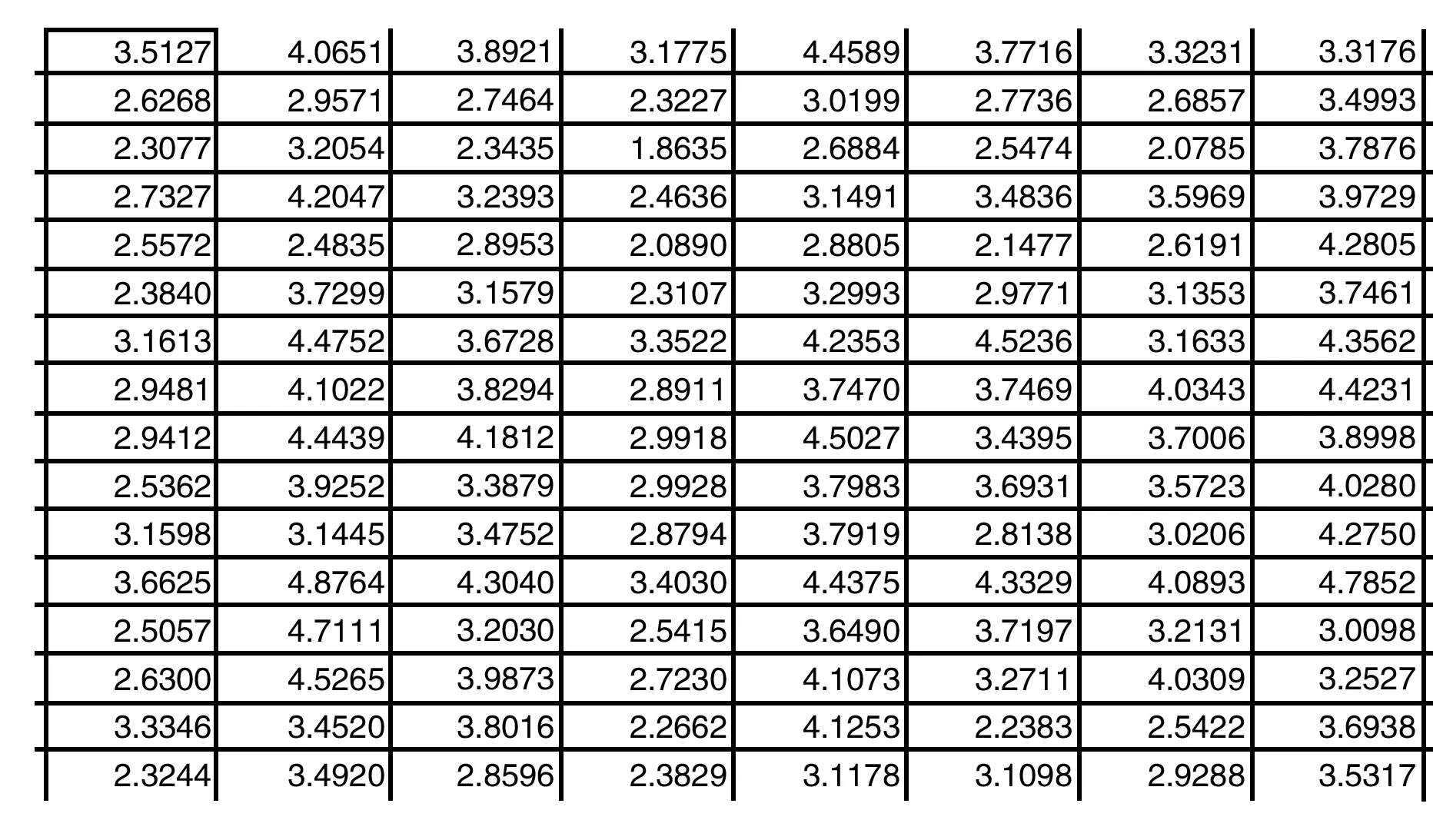
圖2 填充后的結果

二、系統設計

以某個電影數據庫為例，通過系統如下的設計原理：第一，將己有數據載入，并進行預處理；第二，協同過濾算法，構造代價函數和梯度函數；第三，梯度下降法求解參數；第四，參數對用戶的愛好進行預測。設計電影為代價函數中的X的前綴，對應的評分就是數據矩陣,上千部電影，900+用戶評分。正則化之后的數據矩陣如圖1所示。那么推薦系統需要做的工作就是求出theta,然后對數字為0的地方進行填充，得到結果如圖2所示。

對數據再進行一些后續加工處理就可以得到輸出結果，比如對某電影的平均評分，還可以得到某用戶對某些電影的喜好預測等。上述就是協同過濾的全過程。

三、結語

本文提出一種新的電影推薦方法，詳細描述了協同過濾的過程及系統的設計。但是由于時間的限制，電影系統的功能只實現了簡單的電影推薦以及電影信息查看。在以后的研究中需進一步完善系統的功能，使推薦系統在實際生活中，為用戶提供更多的功能選擇。