挑戰中感悟知識 反思中提升能力

許 燕

在自然界和人類社會生活中，嚴格確定的現象十分有限，不確定的隨機現象卻大量存在。概率是對隨機現象的一種描述，它可以為人們合理、理性地決策提供依據。學完了“認識概率”這一章，你對概率的認識有多少呢？本文整理了同學們在平時作業中常出現的幾種典型錯誤，并對錯誤的原因進行分析。聰明的你不妨對照一下！

一、挑戰中感悟知識

專題1 事件類型的確定

例1下列事件中，確定事件有（ ）個。

（1）“飛人”劉翔110米跨欄，只用了6秒鐘；（2）天陰了，將會下雨；（3）一個數的平方一定不是負數；（4）字母a表示一個數，則-a表示負數；（5）兩條線段可以組成一個三角形。

A.4個 B.3個 C.2個 D.1個

【錯解】A或C或D。

【正解】B。

【學生自述】對確定事件理解不透徹。

【點評】（2）（4）是不確定事件；（1）（5）是確定事件中的不可能事件；（3）是確定事件中的必然事件。必然事件和不可能事件統稱為確定事件。所以確定事件有3個。答案選B。

專題2 比較隨機事件發生的可能性的大小

例2如果一個事件不發生的概率為99%，那么這個事件（ ）。

A.必然發生 B.不可能發生

C.發生的可能性很大 D.發生的可能性很小

【錯解】A或B或C。

【正解】D。

【學生自述】如果一個事件不發生的概率為99%，則誤認為該事件就不可能發生。

【點評】要知道隨機事件發生的可能性有大有小。此隨機事件不發生的概率為99%，只能說明其發生的可能性很小，但并不是不可能發生。所以答案選D。

例3世界杯決賽有8個小組，每個小組有4個隊。小組進行單循環（每個隊都與該小組的其他隊比賽一場）比賽，選出2個隊進入16強，勝一場得3分，平一場得1分，負一場得0分。（1）求每個小組共比賽多少場？（2）在小組比賽中，現有一個隊得到6分，該隊出線是一個確定事件，還是不確定事件？

【錯解】（1）12場；（2）是確定事件。

【正解】（1）6場 ；（2）是不確定事件。

【學生自述】（1）忽視了是單循環比賽；（2）考慮問題不全面。

【點評】（1）由于是單循環比賽，所以每一個小組的4個球隊應該比賽4×3÷2=6（場）。（2）因為總共有6場比賽，一個球隊每場比賽最多可得3分，則6場比賽最多可得3×6=18分。現有一個隊得6分，還剩下12分，則可能有2個隊同時得6分。故不能確保該隊出線。因此該隊出線是一個不確定事件。

專題3 體會概率的現實意義，解決實際問題

例4在2012—2013賽季NBA常規賽中，科比罰球的命中率大約是83.3%。下列說法錯誤的是（ ）。

A.科比罰球投籃2次，一定全部命中

B.科比罰球投籃2次，不一定全部命中

C.科比罰球投籃1次，命中的可能性較大

D.科比罰球投籃1次，不命中的可能性較小

【錯解】B或C或D。

【正解】A。

【學生自述】不能正確理解概率的現實意義。

【點評】由科比罰球投籃的命中率來估計科比當前投籃的命中情況，雖然以往命中率為83.3%比較高，但不表示一定會命中。所以答案A是錯誤的。

專題4 概率與頻率的關系

例5“六一”兒童節期間某玩具超市設立了一個如下圖所示可以自由轉動的轉盤，開展有獎購買活動。顧客購買玩具就能獲得一次轉動轉盤的機會。當轉盤停止時，指針落在某一區域就可以獲得相應獎品（鉛筆或文具盒）。下表是該活動的一組統計數據。下列說法正確的有（ ）個。

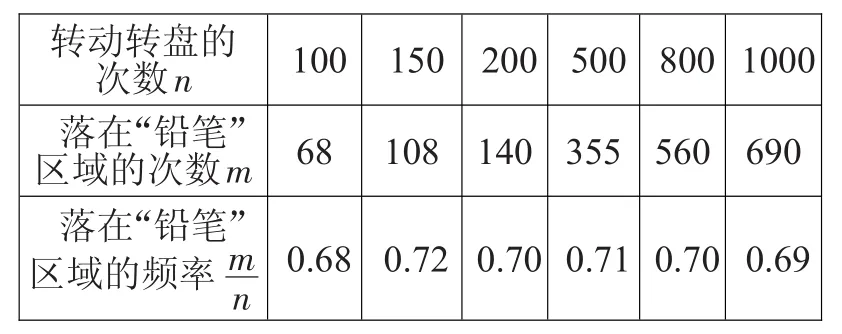
（1）當n很大時，估計指針落在“鉛筆”區域的頻率大約是0.70；（2）假如你去轉動轉盤一次，獲得鉛筆的概率大約是0.70；（3）如果轉動轉盤2000次，指針落在“文具盒”區域的次數大約有600次；（4）轉動轉盤10次，一定有3次獲得文具盒。

A.4個 B.3個 C.2個 D.1個

【錯解】A或C或D。

【正解】B個。

【學生自述】選錯的原因是對頻率和概率的關系沒有理解透徹。

【點評】在充分多次試驗中，一些事件的頻率總在一個定值附近擺動，試驗次數越多，擺動幅度越小，這個性質稱為頻率的穩定性，所以（1）是正確的，此時可用頻率的穩定值來估計事件的概率。轉盤指針落在“鉛筆”區域和“文具盒”區域的概率分別為0.70和0.30，因此（2）（3）是正確的。（4）轉動轉盤10次，一定有3次獲得文具盒的說法是錯誤的。所以說法正確的有3個，答案選B。

二、反思中提升能力

1.下列成語，刻畫的是必然事件的是____，刻畫的是不可能事件的是________，刻畫的是隨機事件的是_______。（選填序號）

（1）萬無一失；（2）勝敗乃兵家常事；（3）水中撈月；（4）十拿九穩；（5）海枯石爛；（6）守株待兔；（7）百戰百勝；（8）九死一生。

2.王強與李剛兩位同學在學習“概率”時，做試驗來拋一枚質地均勻的正方體骰子。他們共拋了54次，向上點數出現的次數如下表：

（1）請計算向上點數為“3”的頻率及向上點數為“5”的頻率；（2）王強說：“根據試驗結果可知，一次試驗中出現向上點數為5的概率最大。”李剛說：“如果拋540次，那么出現向上點數為6的次數正好是100次。”請判斷王強和李剛說法的對錯。

【答案】1（.1）（7）；（3）（5）；（2）（4）（6）（8）。