基于鍵合圖模型的SHA/EMA余度 系統的故障診斷

劉宏飛， 于黎明， 張柱， 閻旭棟， 韓旭東

(1. 北京航空航天大學自動化科學與電氣工程學院, 北京 100083； 2. 北京航空航天大學 飛行學院, 北京 100083)

隨著多電飛機概念的提出，功率電傳作動系統開始越來越多地應用在飛機上，目前應用最廣泛的兩類功率電傳作動器是電靜液作動器(EHA)和機電作動器(EMA)。由于一些尚未解決的技術難題(如滾柱絲杠卡死)存在，功率電傳作動器還不能完全取代傳統的液壓伺服作動器(SHA)，而是通常采用與技術成熟的SHA組合成非相似余度作動系統的方法來進行過渡[1]。非相似余度結構可有效地避免共性故障，但余度結構帶來的元部件數量的增加會增加系統發生故障的可能性[2]，所以對傳統液壓作動器SHA與先進的功率電傳作動器EMA組成的余度系統進行故障診斷具有一定的預研價值。

功率鍵合圖是一種基于能量守恒原理的建模方法，可以方便地建立多能域系統的統一模型[3]。由功率鍵合圖模型中的因果關系可以直接推導出反映系統故障特征的解析冗余關系式(ARR)，從而方便對系統進行故障診斷和隔離(FDI)。文獻[4]應用全局ARR對不同工作模式下的混合動力液壓轉向系統進行了故障診斷。文獻[5]采用雙因果鍵合圖方法增加了系統可隔離故障數量。文獻[6]將鍵合圖與BP神經網絡相結合，研究了并網逆變器的故障診斷。文獻[7]建立了EHA的鍵合圖模型并對液壓缸內泄漏故障進行了診斷。已有的研究多是針對系統中可隔離故障的診斷，對于不可隔離故障的診斷卻鮮有提到，而在不可隔離故障中，某些典型故障仍然存在較大的診斷價值。

本文提出的基于鍵合圖模型的故障診斷方法分為3步：第1步，建立SHA/EMA余度系統的行為模型，模擬系統的實際工作情況[8]；第2步，進行理論推導，得到故障診斷的理論依據；第3步，通過仿真對故障進行診斷。其中第2步最關鍵，完成該步驟后可以將系統中所有的故障分為可隔離故障和不可隔離故障，本文選擇典型的可隔離故障(液壓缸內泄漏、滾柱絲杠失步)和不可隔離故障(電液伺服閥內泄漏、滾柱絲杠卡死)進行了仿真驗證。

1 行為模型

圖1為SHA/EMA余度系統的原理圖，圖中上半部分為SHA，電液伺服閥控制液壓缸輸入流量驅動作動筒運動；下半部分為直驅式EMA，電機的旋轉運動通過滾柱絲杠轉化為直線運動。圖中：iv為輸入電液伺服閥的電流；U為輸入電機的 電壓；xs為滾柱絲杠的位移；xl和Fl分別為舵面的位移和其所受的負載力；xp為液壓缸活塞桿的位移；FE和FH分別為滾柱絲杠與舵面間的作用力和活塞桿與舵面間的作用力。2個通道在舵面處采用力綜合的方式，共同驅動負載。

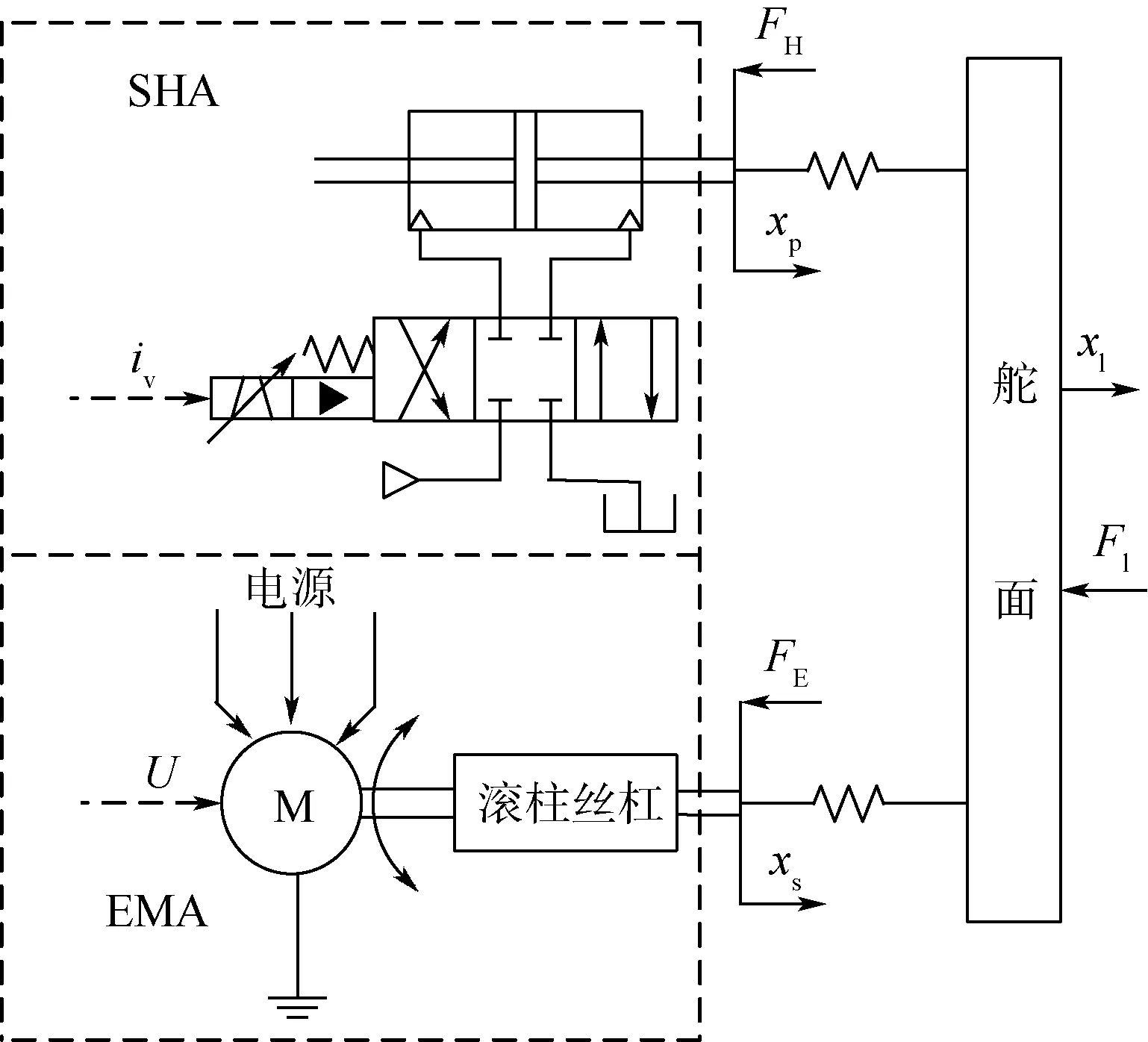
圖1 SHA/EMA余度系統的原理圖Fig.1 Schematic diagram of SHA/EMA redundant system

依次建立系統中電液伺服閥、液壓缸、電機、滾柱絲杠和舵面的鍵合圖模型，將其按照工作原理連接起來，得到SHA/EMA余度系統的鍵合圖模型，如圖2所示。為獲得系統中所有的故障信息，在圖2中設置了8個傳感器Df1、Df2、De1、Df3、De2、De3、Df4和De4，分別測量電機的感應電流(Im)、電機轉速(ω)、滾柱絲杠間的作用力(Fs)、滾柱絲杠移動速度(vs)、滾柱絲杠與舵面間的作用力(FE)、活塞桿與舵面間的作用力(FH)、活塞桿移動速度(vp)、液壓缸兩腔壓力差(PL1)8個物理量。

建立了SHA/EMA余度系統的鍵合圖模型后，需要驗證該模型的可用性。查閱相關文獻[9-10]，得到SHA和EMA的參數如表1所示。代入表1中的參數，對系統模型進行仿真驗證。

SHA/EMA余度系統開環下的輸出力曲線和位移曲線分別如圖3和圖4所示。由圖3可知，SHA的響應速度快于EMA，最初EMA作為負載的一部分被SHA拉動，經過0.2 s后EMA才開始產生推力。由圖4可知，SHA和EMA具有很好的同步性，位移偏差基本為零；在4 s處加入10 kN的外負載后，由于未加閉環控制，作動桿會被反推著運動，產生一定的反向位移，最終達到穩定狀態。圖3和圖4中的曲線驗證了該模型的可用性。

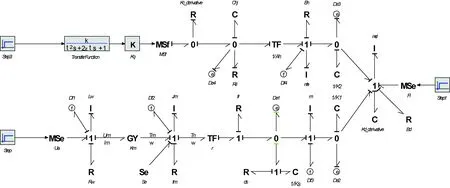
圖2 SHA/EMA余度系統的鍵合圖模型Fig.2 Bond graph model of SHA/EMA redundant system

表1 SHA/EMA余度系統的仿真參數Table 1 Simulation parameters of SHA/EMA redundant system

圖3 SHA/EMA余度系統的開環輸出力曲線Fig.3 Curves of open-loop output force of SHA/EMA redundant system

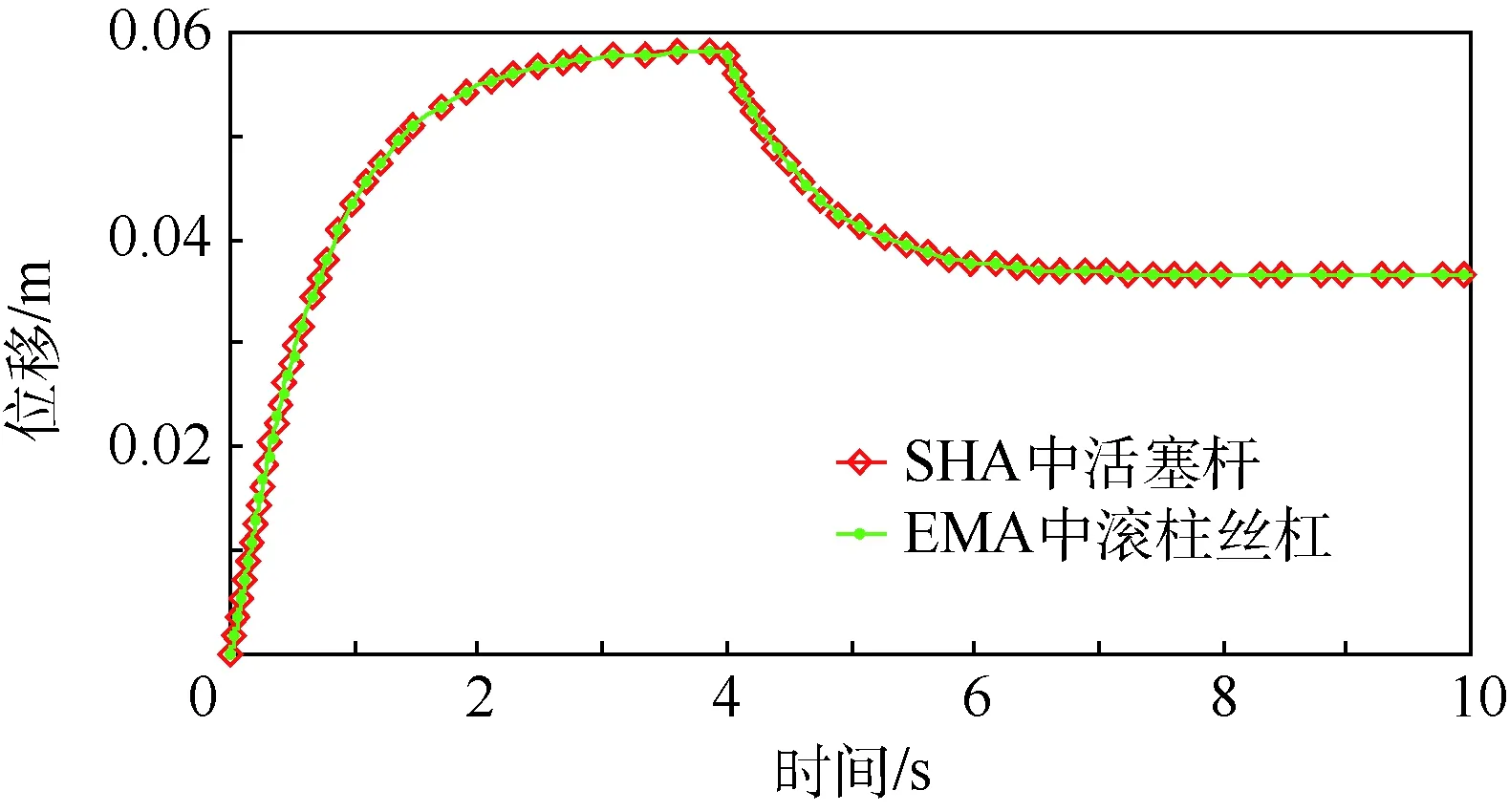
圖4 SHA/EMA余度系統的開環位移曲線Fig.4 Curves of open-loop displacement of SHA/EMA redundant system

2 理論推導

故障診斷的理論推導分為3步：第1步，根據實際系統的行為模型建立診斷鍵合圖模型；第2步，推導ARR，預測殘差變化趨勢；第3步，創建故障特征矩陣(FSM)，作為診斷依據。

2.1 診斷鍵合圖

首先根據因果關系倒置法[11]，將圖2中所有的儲能元件(I,C)由積分因果關系變換成微分因果關系，然后將傳感器變換成相應的虛擬源，最后修改其他鍵合圖元的因果關系以避免沖突，由此即可得到SHA/EMA余度系統的診斷鍵合圖模型，如圖5所示。在該圖中，虛擬源為診斷鍵合圖的輸入信號，其值來自行為模型傳感器的輸出值；與虛擬勢(流)源相連鍵上的流(勢)即為系統的殘差，正常狀態下其值都為零。為了方便2.2節中ARR的推導，這里給功率鍵指定了序號，圖中一共有36根功率鍵。

2.2 解析冗余關系式

ARR是由已知變量(測量值和已知輸入)表示的約束關系式，代表一組已知變量之間的各種約束關系[12]。ARR的數值即殘差，在正常情況下，殘差為零；發生故障時，殘差不為零。SHA/EMA余度系統的診斷鍵合圖模型中共有8個虛擬源，最多可以推導出8個ARR，推導過程中出現的ei(fi)表示第i根鍵上的勢(流)。下面將依次對這些解析冗余關系式進行推導。

1) 電機感應電流的ARRf1

e1-e2-e3-e4=0

(1)

根據圖5中各元部件的因果關系以及特性方程可知：

(2)

聯立式(1)、式(2)消除方程中的未知變量，可以得到電機感應電流虛擬源處的解析冗余關系式(ARRf1)為

(3)

2) 電機角速度的ARRf2

e5-e6+e7-e8-e9=0

(4)

圖5 SHA/EMA余度系統的診斷鍵合圖模型Fig.5 Diagnostic bond graph model of SHA/EMA redundant system

根據圖5中各元部件的因果關系以及特性方程可知：

(5)

式中:r為滾柱絲杠導程P與2π的比值。聯立式(4)、式(5)消除方程中的未知變量，可以得到電機角速度虛擬源處的解析冗余關系式(ARRf2)為

(6)

3) 滾柱絲杠間作用力的ARRe1

f12-f13-f16=0

(7)

根據圖5中各元部件的因果關系以及特性方程可知：

(8)

式中：ds為滾柱絲杠間的阻尼系數。

聯立式(7)、式(8)消除方程中的未知變量，并在等式兩邊同時求導后可以得到滾柱絲杠間作用力虛擬源處的解析冗余關系式(ARRe1)為

(9)

4) 滾柱絲杠移動速度的ARRf3

e16-e17-e18=0

(10)

根據圖5中各元部件的因果關系以及特性方程可知：

(11)

聯立式(10)、式(11)消除方程中的未知變量，可以得到滾柱絲杠移動速度虛擬源處的解析冗余關系式(ARRf3)為

(12)

5) 滾柱絲杠與舵面間作用力的ARRe2

f18-f19-f20=0

(13)

根據圖5中各元部件的因果關系以及特性方程可知：

(14)

式中：Bd為舵面等效黏性阻尼系數；Kd為舵面平穩負載的比例系數。

聯立式(13)、式(14)消除方程中的未知變量，并在等式兩邊同時求導后可以得到滾柱絲杠與舵面間作用力虛擬源處的解析冗余關系式(ARRe2)為

(15)

6) 活塞桿與舵面間作用力的ARRe3

f27-f26-f25=0

(16)

根據圖5中各元部件的因果關系以及特性方程可知：

(17)

聯立式(16)、式(17)消除方消除方程中的未知變量，并在等式兩邊同時求導后可以得到活塞桿與舵面間作用力虛擬源處的解析冗余關系式(ARRe3)為

(18)

7) 活塞桿移動速度的ARRf4

e30-e29-e28-e27=0

(19)

根據圖5中各元部件的因果關系以及特性方程可知：

(20)

聯立式(19)、式(20)消除方程中的未知變量，可以得到活塞桿移動速度虛擬源處的解析冗余關系式(ARRf4)為

(21)

8) 液壓缸兩腔壓力差的ARRe4

f34-f33-f32-f31=0

(22)

根據圖5中各元部件的因果關系以及特性方程可知：

(23)

式中：xv為電液伺服閥的閥芯位移。

聯立式(22)、式(23)消除方程中的未知變量，可以得到液壓缸兩腔壓力差虛擬源處的解析冗余關系式(ARRe4)為

(24)

2.3 故障特征矩陣

診斷出故障后，需要確定系統的哪個部分出現了故障，這一過程稱為故障隔離，故障隔離可以通過創建FSM來完成。FSM是一個二進制矩陣，描述了每個殘差對物理設備、傳感器，作動器和控制器中各種故障的結構靈敏度[13]。FSM可以直接根據2.2節所推導出的ARR構造，SHA/EMA余度系統的故障特征矩陣如表2所示。

表2中每一行的8個殘差值(rf1～re4)組成對應參數的故障特征向量；最后2列Db和Ib分別表示故障的可檢測性和可隔離性，取值為1表示故障可檢測或可隔離。由表2可以看出，系統中所有物理參數引起的參數故障全部可檢測，并且在單故障假設下有4組參數故障可隔離。可隔離故障有液壓缸內泄漏(Ah,Ril)、液壓缸阻滯(Bh)、電機失磁(Km)和滾柱絲杠失步(r,Ks)。

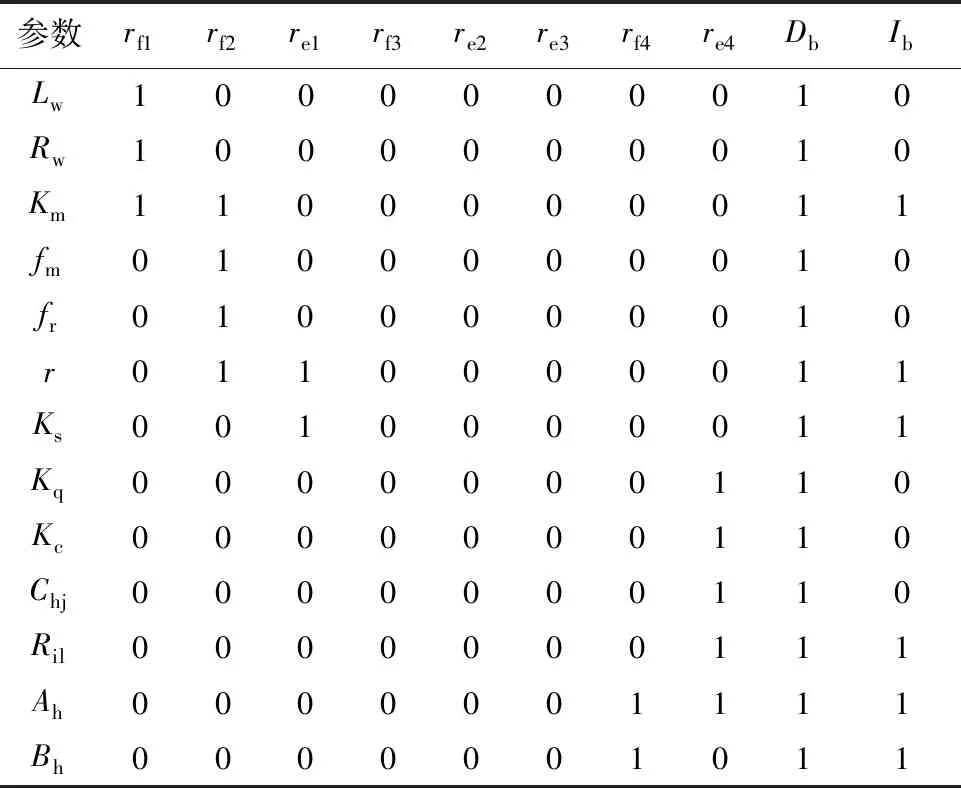
表2 SHA/EMA余度系統的故障特征矩陣Table 2 FSM of SHA/EMA redundant system

3 仿真分析

在單故障假設下，FSM將故障分為可隔離故障和不可隔離故障。可隔離故障可以直接使用診斷鍵合圖來仿真驗證，不可隔離故障將通過參數估計的方法對故障參數進行辨識。下面分別進行介紹。

3.1 可隔離故障

以可隔離故障中的液壓缸內泄漏(Ah,Ril)和滾柱絲杠失步(r,Ks)為例進行仿真驗證。將SHA/EMA余度系統的行為模型和診斷鍵合圖模型聯立，得到余度系統的故障診斷仿真模型，見圖6。通過在系統的行為模型中改變參數值注入故障，測得圖中8個虛擬源處的殘差值，并將其組成故障特征向量后與FSM進行對比就能隔離故障。

系統無故障時的殘差曲線如圖7所示，該圖顯示系統中所有的殘差值都為零，即故障特征向量[rf1,rf2,re1,rf3,re2,re3,rf4,re4]=[0, 0, 0, 0, 0, 0, 0, 0]，表示系統中沒有出現故障，這與無故障假設相吻合。

1) 液壓缸內泄漏(Ah,Ril)

液壓缸內泄漏主要是由液壓油中的雜質顆

粒在作動桿往復運動過程中磨損密封圈和筒壁后形成的縫隙造成的[14]，通過減小活塞有效面積Ah并且增大液壓缸內泄漏系數Ril的值就能注入液壓缸內泄漏故障。液壓缸內泄漏故障的殘差曲線如圖8所示。

由圖8可知，在這8個殘差值中除了rf4和re4，其余6個殘差值都非常小，可以忽略不計，則內泄漏故障對應的故障特征向量為[rf1,rf2,re1,rf3,re2,re3,rf4,re4]=[0, 0, 0, 0, 0, 0, 1, 1]，這與FSM中Ah和Ril的故障特征向量一致，表明液壓缸內泄漏故障被成功隔離。

2) 滾柱絲杠失步(r,Ks)

滾柱絲杠失步主要由二者接觸表面剛度下降或者磨損所引起[15]，與滾柱絲杠間的剛度Ks和傳動比r有關，通過減小r和Ks的值可以注入失步故障，殘差曲線如圖9所示。

圖9中顯示，殘差值rf2和re1不為零，其余6個殘差值大小可以忽略不計，故障特征向量[rf1,rf2,re1,rf3,re2,re3,rf4,re4]=[0, 1, 1, 0, 0, 0, 0, 0]，與FSM中r和Ks的綜合故障特征向量一致，說明滾柱絲杠失步(r,Ks)故障被成功隔離。

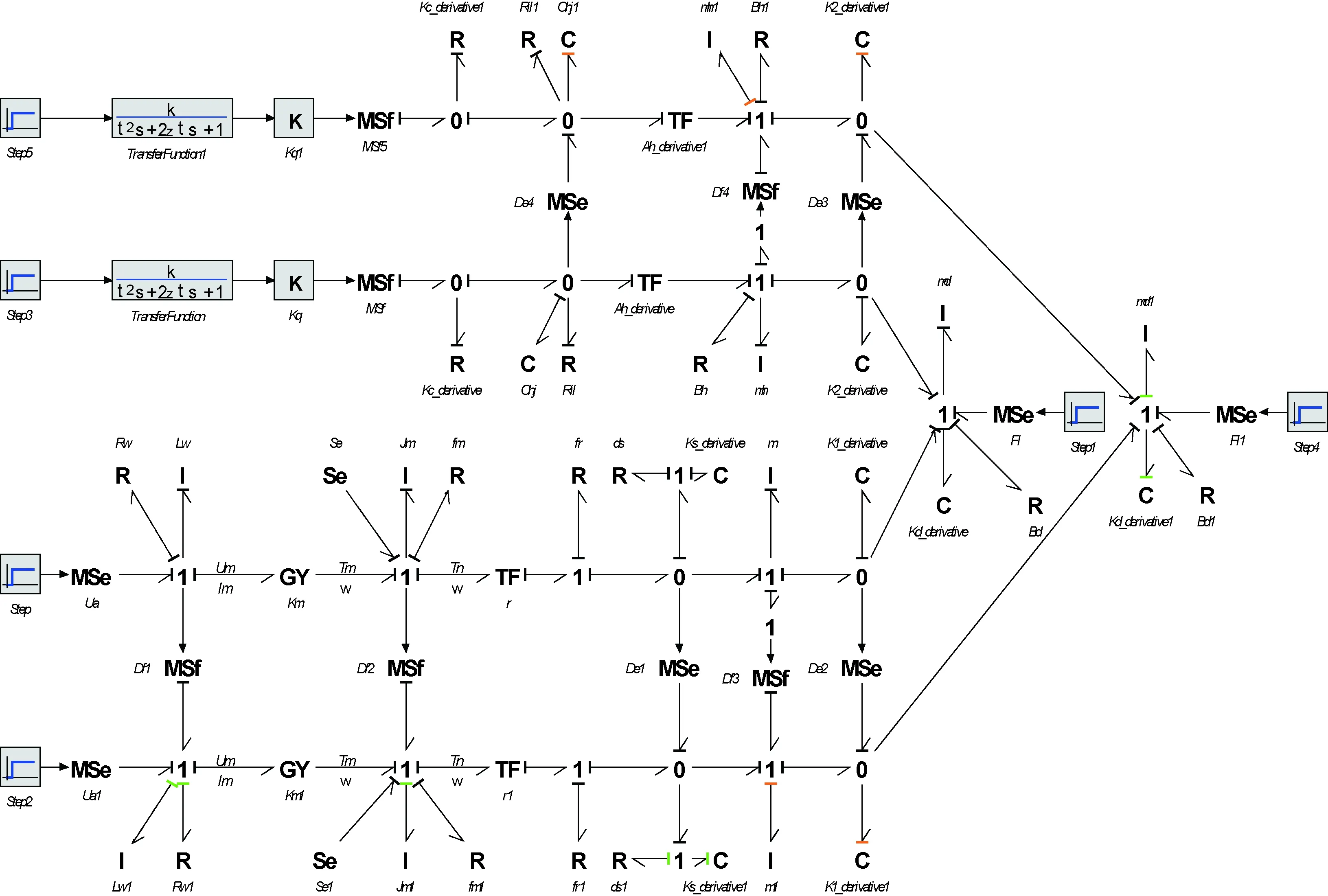
圖6 SHA/EMA余度系統的故障診斷仿真模型Fig.6 Simulation model for fault diagnosis of SHA/EMA redundant system

3.2 不可隔離故障

FSM中除4組可隔離故障外，其余均為不可隔離故障。由于ARR是殘差的計算式，利用ARR對故障參數進行參數估計可以診斷出不可隔離故障。下面對電液伺服閥內泄漏(Kc,Kq)和滾柱絲杠卡死(fr)這2種典型故障進行參數估計。

1) 電液伺服閥內泄漏(Kc,Kq)

電液伺服閥內泄漏故障主要是由于閥芯與閥

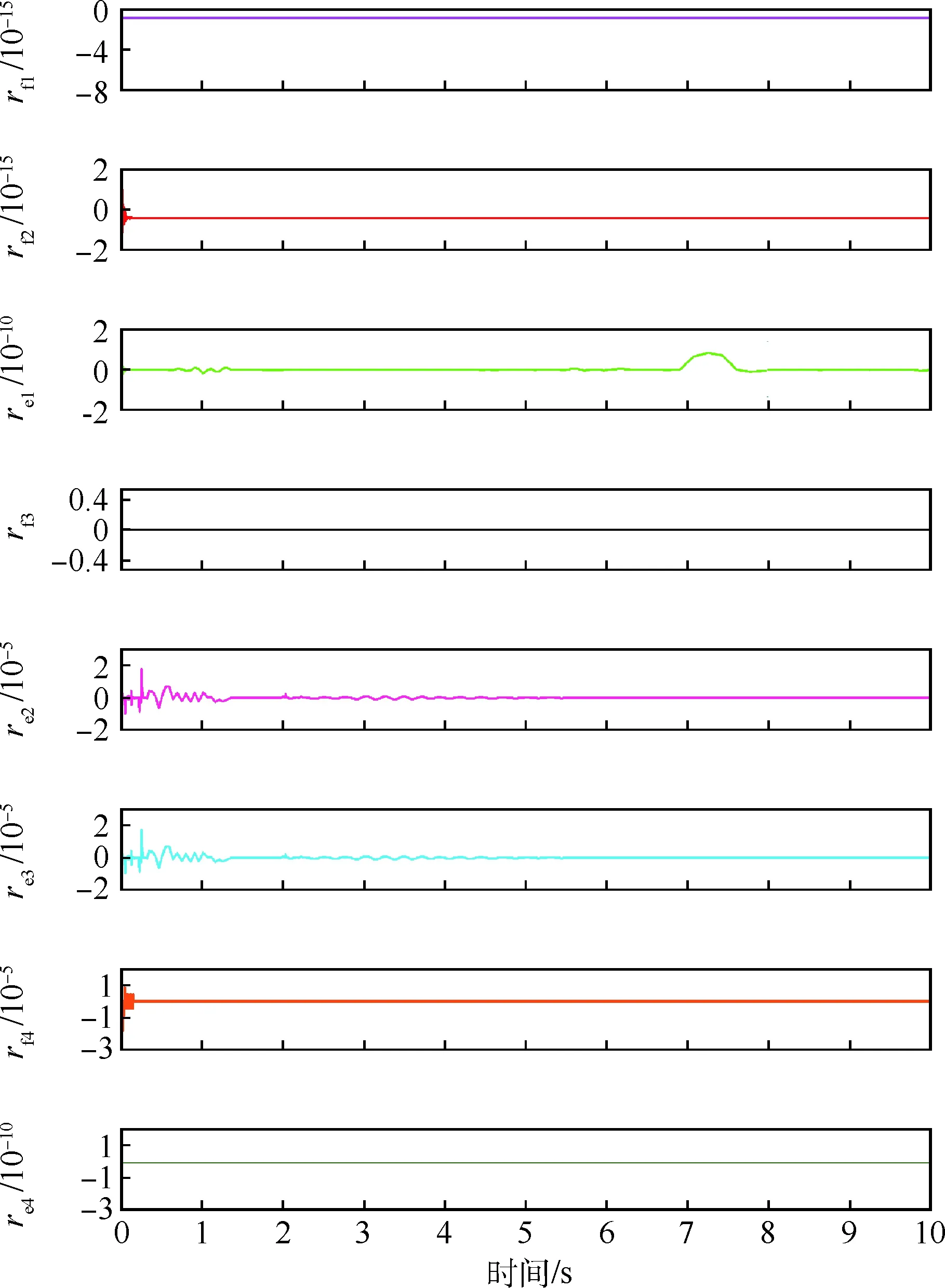
圖7 SHA/EMA余度系統無故障時的殘差曲線Fig.7 Residual curves of SHA/EMA redundant system without fault

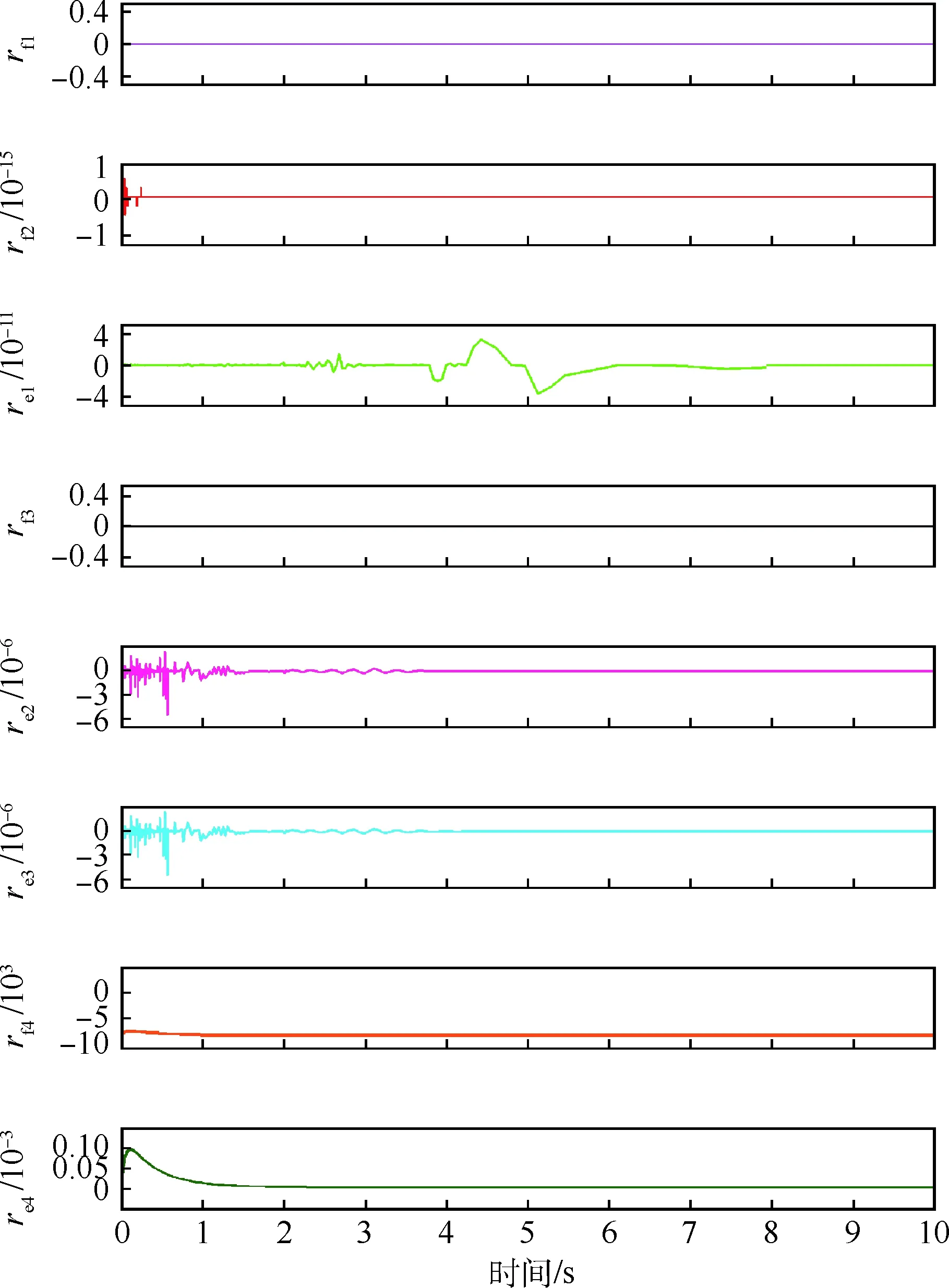
圖8 液壓缸內泄漏故障的殘差曲線Fig.8 Residual curves of internal leakage fault in hydraulic cylinder

體間的磨損引起的，與電液伺服閥的流量增益Kc和流量-壓力系數Kq有關，通過減小二者的值可以注入電液伺服閥內泄漏故障。對Kc和Kq所在的式(24)編寫算法調用已知參數與傳感器測量值，得到電液伺服閥內泄漏故障的參數估計結果如圖10所示。

由圖10可知，Kq和Kc的穩態估計值分別為2.65和1.723×10-11，其標稱值分別為2.7和1.75×10-11，計算得出Kq和Kc穩態估計值的相對誤差分別為1.85%和1.54%，均不超過5%，屬于可接受范圍，則電液伺服閥內泄漏的故障參數被成功隔離。

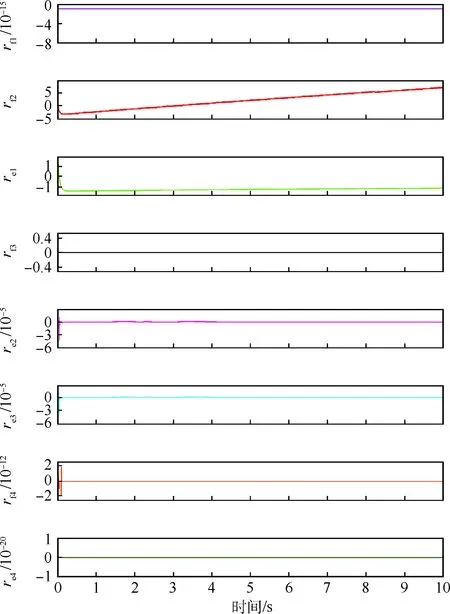
圖9 滾柱絲杠失步故障的殘差曲線Fig.9 Residual curves of out-of-step fault in roller screw

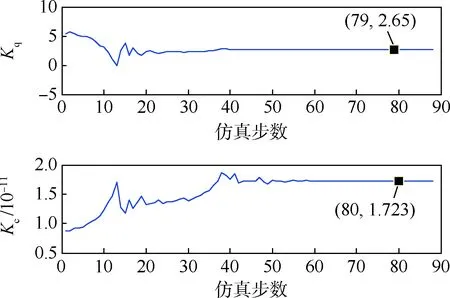
圖10 電液伺服閥內泄漏故障的參數估計Fig.10 Parameter estimation of internal leakage fault in electro-hydraulic servo valve

2) 滾柱絲杠卡死(fr)

滾柱絲杠卡死主要是由于運動過程中有外物進入滾動體軌道或者受到外沖擊所引起的，與滾柱絲杠間的黏性摩擦系數fr有關，通過增大fr的值可以注入滾柱絲杠卡死故障。對fr所在的式(6)編寫算法調用已知參數與傳感器測量值，得到滾柱絲杠卡死故障的參數估計結果如圖11所示。

由圖11可知，fr的穩態估計值為0.957 4×104，標稱值為1×104，計算得出fr穩態估計值的相對誤差為4.26%，不超過5%，屬于可接受范圍，表明滾柱絲杠卡死的故障參數被成功隔離。

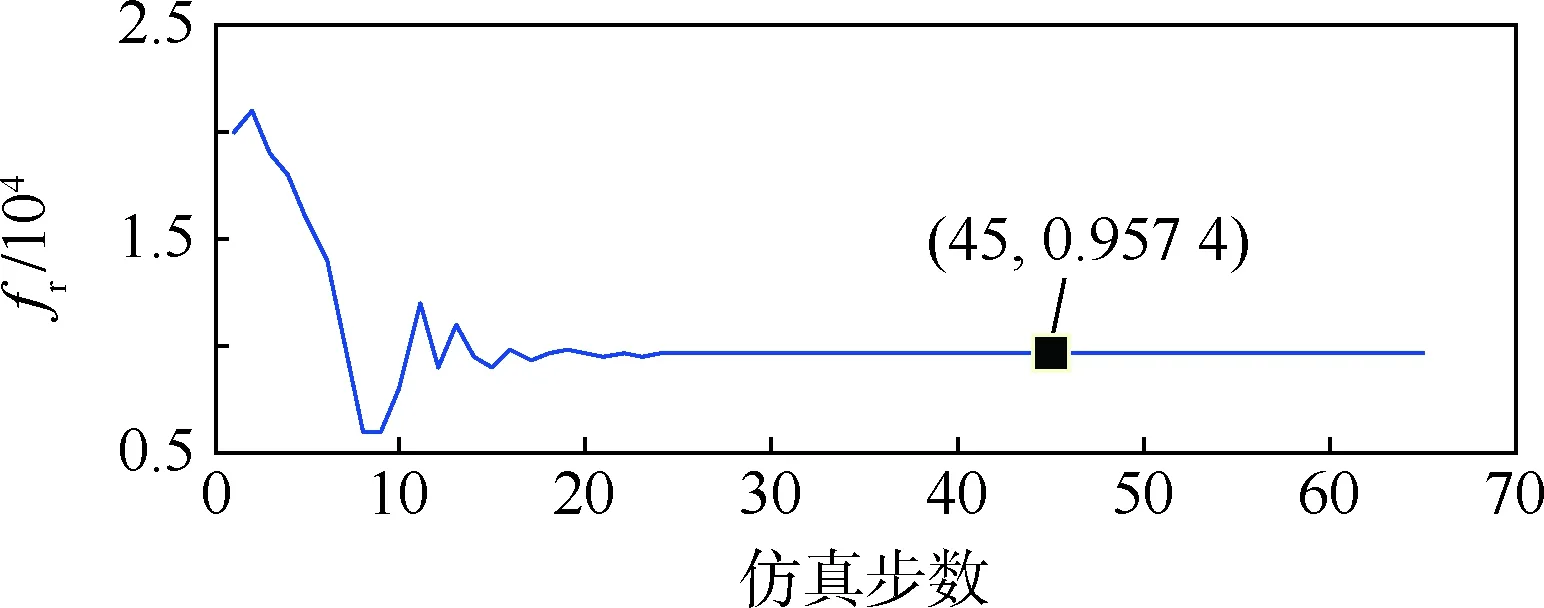
圖11 滾柱絲杠卡死故障的參數估計Fig.11 Parameter estimation of jamming fault in roller screw

4 結 論

本文采用基于鍵合圖模型的故障診斷方法，對SHA/EMA余度系統中的可隔離故障和不可隔離故障進行了診斷，仿真結果表明該方法是有效可行的。

1) 在可隔離故障中，得到液壓缸內泄漏(Ah,Ril)和滾柱絲杠失步(r,Ks)的故障特征向量分別為[0, 0, 0, 0, 0, 0, 1, 1]和[0, 1, 1, 0, 0, 0, 0, 0]，與FSM一致，表明故障被成功隔離。

2) 在不可隔離故障中，電液伺服閥內泄漏和滾柱絲杠卡死的故障參數Kq、Kc和fr穩態估計值的相對誤差分別為1.85%、1.54%和4.26%，均未超過5%，屬于可接受范圍，表明故障被成功隔離。