目標觸底瞬態地震波信號的檢測

余 靖,趙治平

(中國船舶重工集團公司第七一〇研究所,湖北 宜昌 443003)

0 引言

目標觸底是一個較為復雜的過程,目標觸底時,與地面發生沖擊,目標的動能轉換為目標的彈性勢能和海床底土的彈性勢能,且發生回彈,通過多次沖擊,目標的動能轉換為海床底土的彈性勢能和小部分的摩擦熱能,絕大部分的能量以地震波的形式向遠處傳播,地震波的幅度和頻率與目標的密度、尺度、目標的彈性系數以及海床地質等因素有關。通過研究目標觸底地震波信號的傳播特性,對地震波信號進行監測、處理和分析,能夠幫助判斷異常信號的產生是否是由敏感活動引起的,并判斷出敏感活動的位置,從而提升監測效率[2]。

基于高階累積量的信號分析可便于研究和分析信號更進一步的統計特性。利用高階統計量可以在信號檢測、參數估計、信號重構問題中抑制未知譜特征的高斯噪聲,而且高階譜可以用來檢測時間序列的非線性結構,是辨識一個系統的非線性特征的有力工具。本文采用的雙譜檢測方法就是一種利用高階累積量進行檢測的方法,其理論基礎在于:平穩高斯噪聲的3階以上的高階譜能量為0,而非高斯信號其高階譜不為0。據此可以完成在高斯背景噪聲環境中檢測低信噪比非高斯信號的工作[3]。

1 雙譜檢測理論

1.1 雙譜的定義

k階譜定義為隨機過程{(x)}的k階累積量的k-1維離散時間傅立葉變換,即:

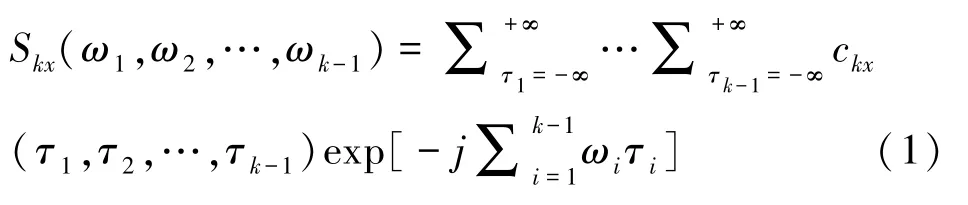
高階譜又被稱為多譜或累積量譜。特別地,我們稱三階譜S3ω(ω1,ω2)叫做雙譜,習慣上記為Bx(ω1,ω2);稱四階譜S4ω(ω1,ω2,ω3)為三譜,習慣上記為Tx(ω1,ω2,ω3)。在高階譜分析中雙譜分析應用最為廣泛。根據高階累積量的性質,我們可得:當加性噪聲是高斯有色噪聲時,高階累積量在理論上可完全抑制噪聲的影響[4-5]。

1.2 基于雙譜的有色高斯噪聲信號檢測

假定有如下二元隨機信號檢測問題:

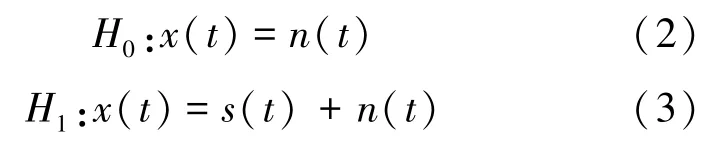
式中:t=1,2,…,N,s(t)為實際信號,且為非高斯的平穩信號;n(t)為高斯噪聲,且信號s(t)與噪聲n(t)是相互獨立的。

若采用傳統的功率譜估計方法, 則有:

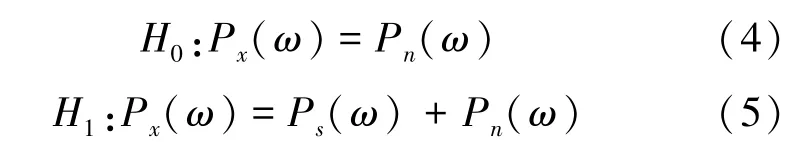
則可得,當信噪比下降時,信號的檢測能力將明顯下降,虛警概率將明顯增大。

若采用雙譜估計方法, 則有:

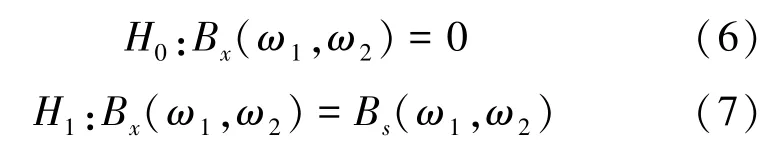
從上式可以看出,只要信號的雙譜信息足夠豐富,即使在信噪比很小的情況下,隨機信號經過雙譜處理后,其信噪比也將大大提高,因此有利于信號的檢測[6]。

2 雙譜估計信號檢測

已知非高斯信號在某些頻率對(ωm,ωn)上的雙譜不為0, 因此,當Bx(ωm,ωn)≡0時判決為H0,即無信號;當Bx(ωm,ωn)≠0時判決為H1,即檢測到有信號,于是上述檢測須排除H0的判決。在紐曼-皮爾森準則下,與判決相關的門限常數由虛警概率決定,檢測性能由判據選擇決定。相應的試驗統計量與閾門值和設定的虛警概率α的關系,可在Hinich-Wilson檢測準則[7]及其相關前提條件來判斷。

設判決門限常數為,在Hinich-Wilson準則下的判決因子為,則排除H0假設時有在判決H1假設時,判決因子T2c服從一定參數下的非中心Fisher分布,從而可得:

其中(ωm,ωn)位于主域內,故:

其中,

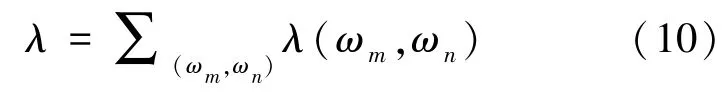
門限由虛警概率決定

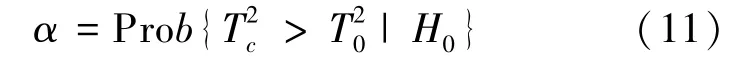
從而:

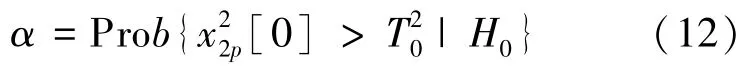
相應的令:

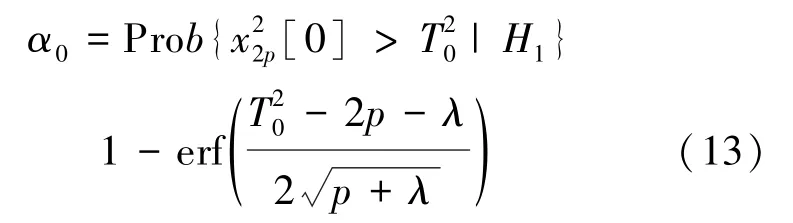
P為頻率對點上的雙譜平均估計值,當P較大且門限值固定不變時,檢測概率為下面的遞增函數:

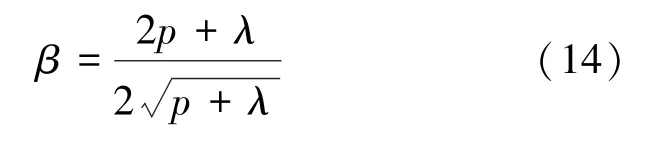
3 雙譜估計信號特征

3.1 高斯帶限噪聲雙譜估計

利用MATLAB產生白噪聲序列,將產生的噪聲通過低通濾波器得到帶限高斯噪聲如圖1,對帶限高斯信號進行直接雙譜估計,得到其雙譜平面圖2和三維圖3。

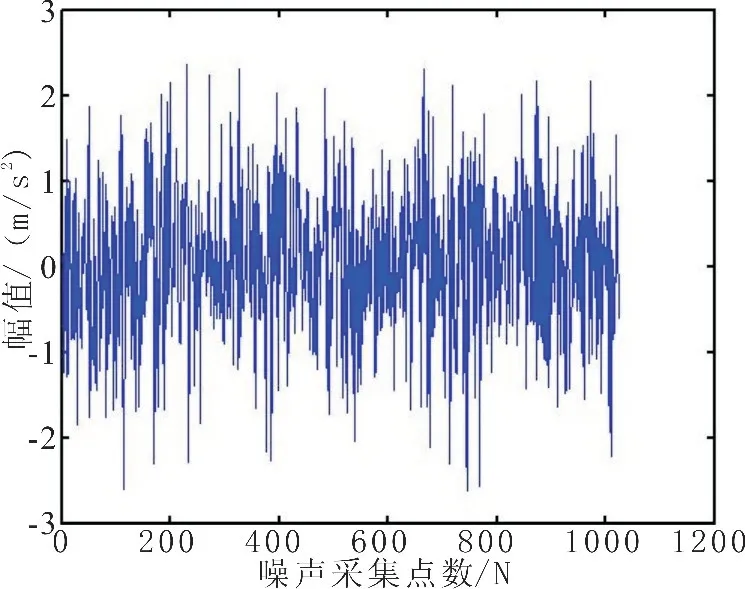
圖1 帶限高斯噪聲波形圖Fig.1 Band-limited Gaussian noise waveform

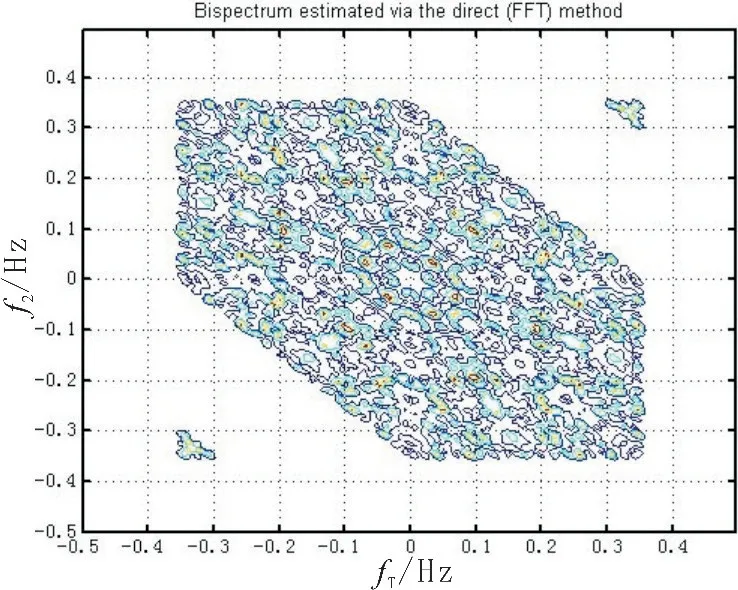
圖2 噪聲雙譜估計平面圖Fig.2 Noise bispectral estimation plan

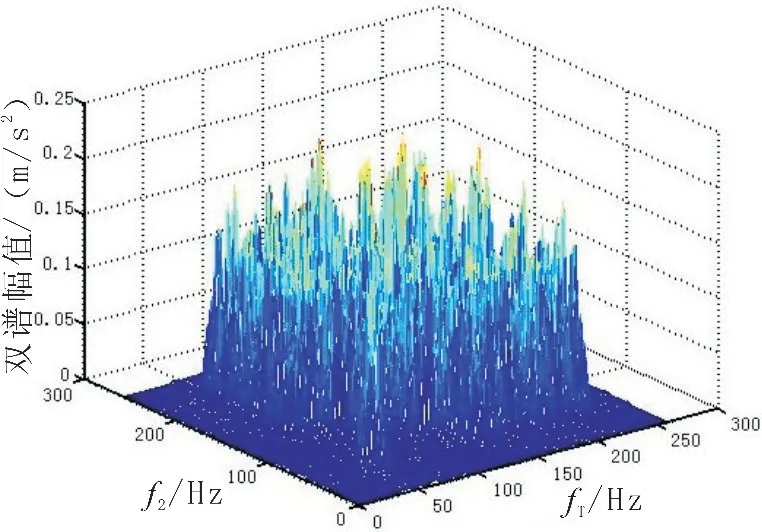
圖3 噪聲雙譜估計三維圖Fig.3 Noise bispectral estimation 3D diagram

3.2 目標下落高度為0.67 m時瞬態信號雙譜估計

以試驗采集到的模擬目標觸底信號為數據樣本,將以上數據樣本簡記為t067,截取其9.15～9.4 s的數據樣本進行雙譜估計:圖3-4為采集到的信號波形,得到其雙譜平面圖3-5和三維圖3-6。

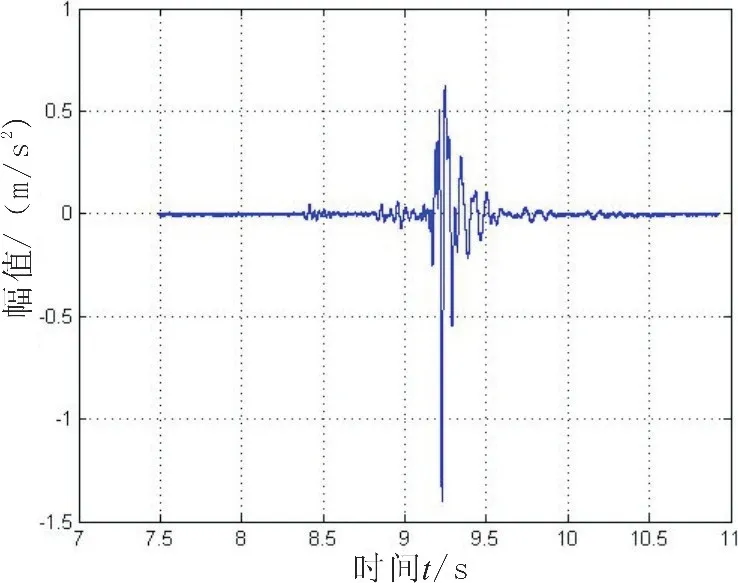
圖4 瞬態信號波形圖Fig.4 Instantaneous signal waveform

圖5 瞬態信號雙譜估計平面圖Fig.5 Instantaneous signal bispectral estimation plan

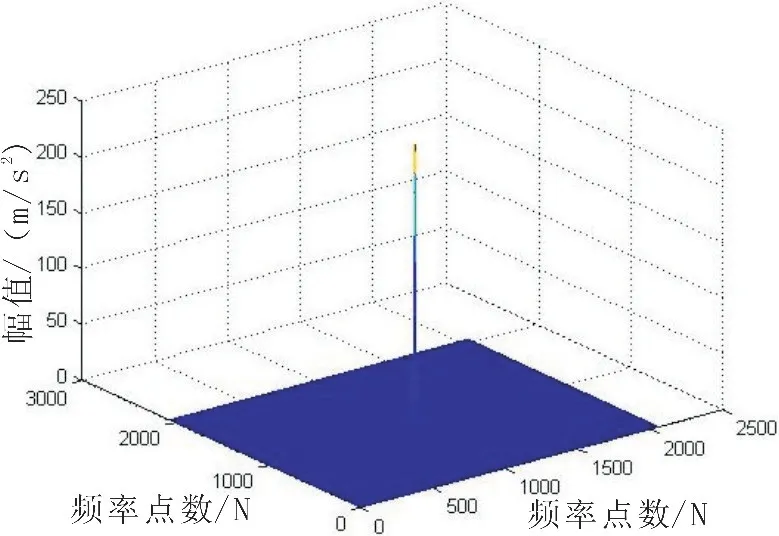
圖6 瞬態信號雙譜估計三維圖Fig.6 Instantaneous signal bispectral estimation 3D diagram

目標觸底產生的瞬態信號混合高斯帶限噪聲的波形如圖7所示,其雙譜估計平面圖和三維圖分別如圖8-9所示。

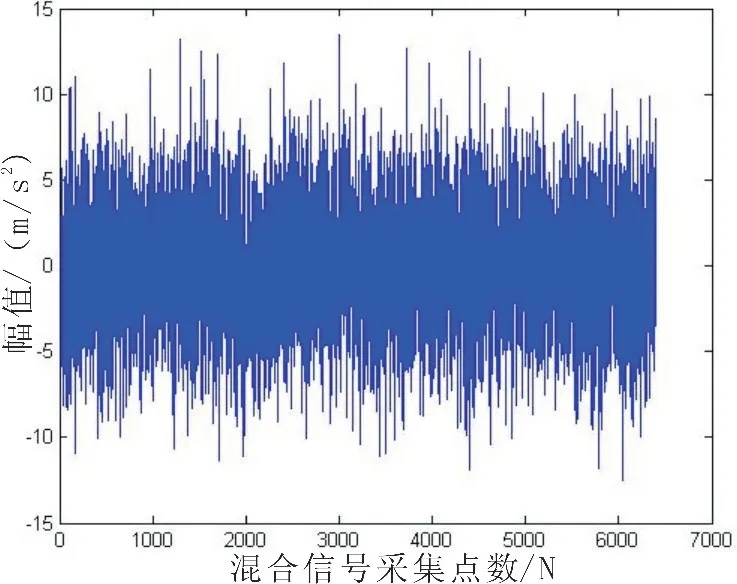
圖7 混合信號波形圖Fig.7 Mixed signal waveform

圖8 混合信號雙譜平面圖Fig.8 Mixed signal bispectral plan

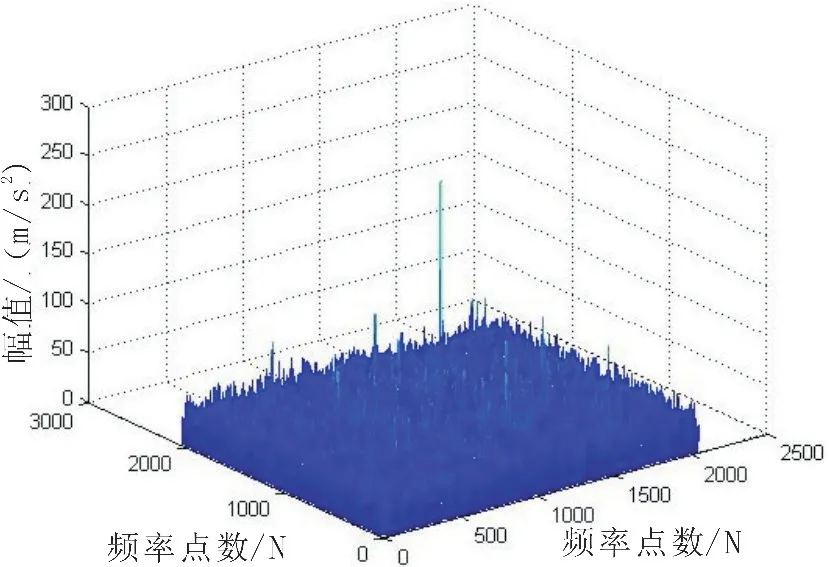
圖9 混合信號雙譜三維圖Fig.9 Mixed signal bispectral 3D diagram

同時,對目標下落高度為1.50 m時的波形(對此段數據記為t150)也進行了上述分析,所得的雙譜分析圖與上述圖類似。從信號雙譜估計結果可以看出,瞬態脈沖噪聲與連續平穩帶限高斯噪聲相比,在雙譜估計值上具有明顯的特征區別:首先,帶限髙斯噪聲的雙譜估計值并不完全等于理論值0,而是具有相對均勻分布的雙譜量,與理論分析有差別,但是其雙譜值在量級上比較小。而在信噪比夠大的情況下,瞬態信號的雙譜估計值在雙譜域坐標零點附近具有峰值,而在其他地方的雙譜值非常小,即輸出具有非常高的信噪比。這一特征與帶限高斯噪聲信號的特征差別非常明顯,可以作為信號檢測的一個判別標志,從而利用雙譜估計從高斯噪聲中檢測出瞬態脈沖信號的存在[8]。

4 雙譜估計檢測仿真

基于高斯噪聲和瞬態脈沖信號的特征差別,完全可以利用信號序列的雙譜估計來實現高斯噪聲背景中檢測非高斯非平穩性瞬態脈沖信號的目的。高斯噪聲理論上雙譜為0,瞬態信號的雙譜為非零。從估計結果來看,帶限高斯噪聲的實際雙譜估計并不是完全等于0,從而導致信號檢測性能受瞬態信號信噪比的影響。與瞬態信號雙譜估計結果相比較,在頻率接近坐標原點的位置上,目標觸底瞬態地震波信號雙譜估計值具有非常明顯的譜線,可以很好地利用這一特點對目標觸底瞬態地震波信號進行有效的檢測。

4.1 t067瞬態信號雙譜估計檢測仿真

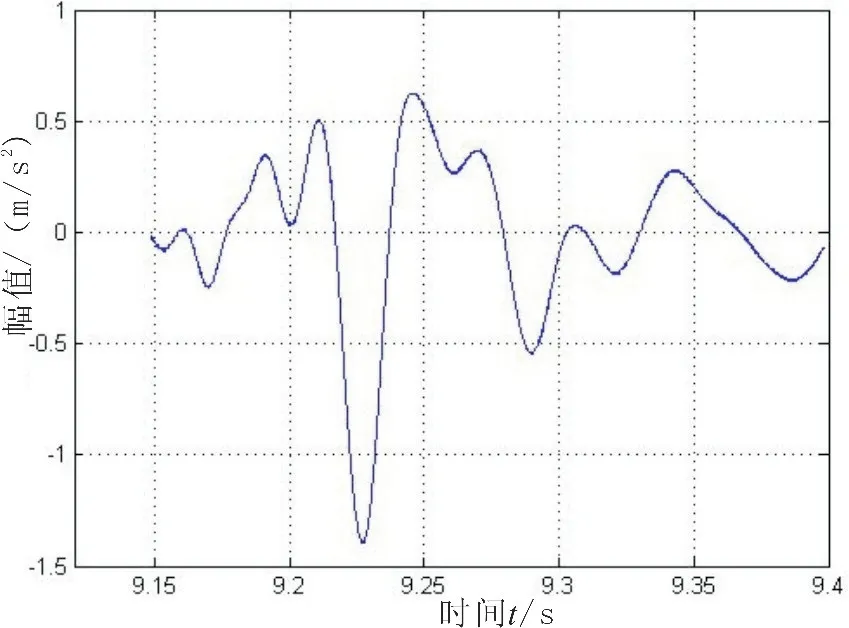
圖10 截取數據段波形圖Fig.10 Data section waveform

將輸入信噪比設為0,噪聲背景以上文所述帶限高斯噪聲為背景噪聲,設置的噪聲幅值為8.5倍的信號幅值,以達到對信號數據的完全覆蓋,對數據t067進行雙譜檢測,其全時段波形如圖4。從觸底產生的一系列信號中提取有用數據段,如圖10。目標觸底瞬態地震波信號雙譜結果假定條件:ω1=ω2＞0,則得到如圖11所示結果。

圖11 w1=w2時截取數據段雙譜值Fig.11 Data section's bispectral values(ω1=ω2)

4.2 瞬態信號雙譜估計檢測仿真

將輸入信噪比設為0,噪聲背景以上文所述帶限高斯噪聲為背景噪聲,設置的噪聲幅值為9.4倍的信號幅值,以達到對信號數據的完全覆蓋,對數據t150進行雙譜檢測,其全時段波形如圖12。

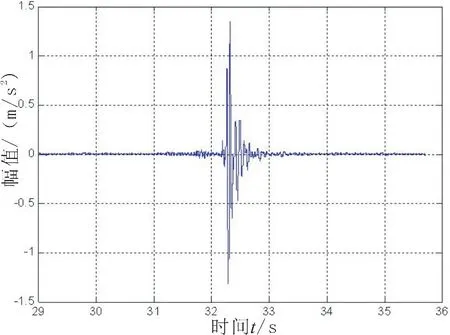
圖12 瞬態信號波形圖Fig.12 Instantaneous signal waveform

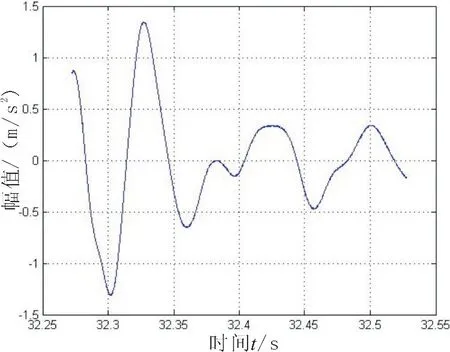
圖13 截取數據段波形圖Fig.13 Data section waveform

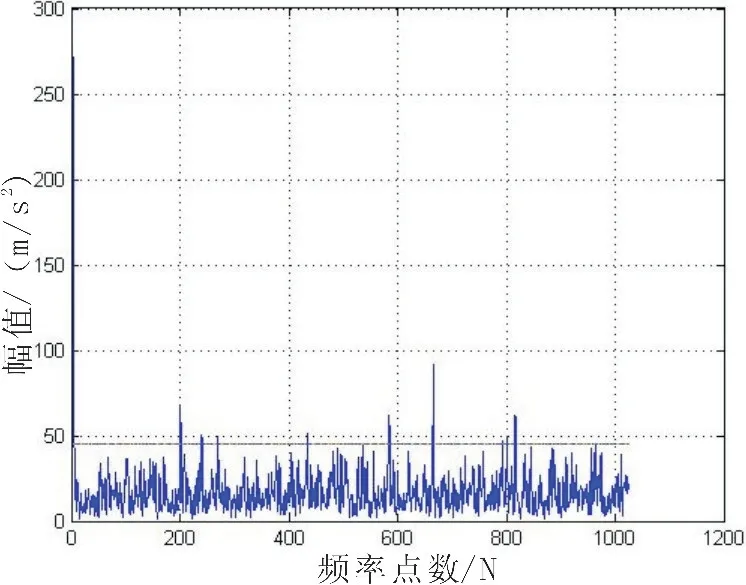
圖14 ω1=ω2時截取數據段雙譜值Fig.14 Data section's bispectral values(ω1=ω2)

從觸底產生的一系列信號中提取有用數據段,如圖13。目標觸底瞬態地震波信號雙譜結果假定條件:ω1=ω2＞0,則得到如圖14所示結果。

經過對2組數據的分析,可得頻率靠近零點附近,雙譜值出現峰值,設定判決區域為試驗全頻率采樣范圍,來進行目標觸底瞬態地震波信號脈沖信號的檢測。

進一步地以不同的信噪比對兩組數據進行仿真試驗,每種不同的信噪比進行仿真試驗不低于50次。

通過具體數據分析,在虛警概率小于3%的條件下,雙譜估計值必須滿足

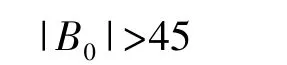
即雙譜估計達到上式可判定為有信號。

據此可以判定出在數據時間段內存在模擬目標觸底瞬態地震波信號。

5 結束語

通過仿真試驗與結果分析,我們得出了與理論分析較一致的結論:雙譜檢測作為一種檢測瞬態信號的手段,具有很好的抗高斯噪聲干擾的能力,在不同的信噪比下,能夠有效地檢測出高斯背景下瞬態信號的存在。后續的學習與探索中可以嘗試將雙譜檢測與其他的檢測方法進一步地相結合,以達到更有效的檢測瞬態信號的目的。