任意姿態下矢量物理量的測量數據修正計算方法探討

程國勝

(中國船舶重工集團公司第七一〇研究所,湖北 宜昌 443003)

0 引言

對矢量物理量的測量,如水中目標的磁場、電場等目標特性的測量,要求測量出該物理量在確定的正交坐標系(通常為當地水平坐標系或者導航坐標系)中的3個方向分量,而在測量實施中,測量傳感器或其安裝平臺的姿態角往往是隨機但可以測量的。因此,在測量數據的處理中,需要對在任意姿態下測量的矢量物理量數據進行修正,即對測量的矢量結果在不同坐標系之間進行轉換。在大多數現有文獻和工程實踐中,修正算法都是直接引用歐拉角旋轉變換公式[1-3]。但是仔細分析,歐拉角旋轉變換公式是基于有先后次序的繞坐標軸的旋轉變換,而實際測量的姿態角,有陀螺儀測量、慣導系統測量、傾斜儀測量、磁場傳感器測量以及多傳感器組合測量,測量傳感器或設備輸出的姿態角有不同的定義,與旋轉歐拉角的定義不一定完全一致。因此,直接引用歐拉角旋轉變換公式進行修正計算,可能存在原理性誤差。在運動載體中的矢量測量以及導航定位中的坐標旋轉變換中也都存在類似的問題。

本文對姿態角定義和傳感器測量原理進行分析,推導姿態角與旋轉歐拉角的關系,進而推導出利用可測量的姿態角進行坐標變換修正的坐標轉換矩陣。

1 坐標系及歐拉旋轉變換

1.1 常用坐標系

在導航和矢量測量中常用的有以下5種正交右手坐標系[4]:

1)地心慣性坐標系OIXIYIZI,簡記為I坐標系;

2)地心地球固定坐標系OEXEYEZE,簡記為E坐標系;

3)導航坐標系ONXNYNZN,簡記為N坐標系,主要用于確定載體相對于東、北和天方向的速度和位置;

4)當地水平坐標系OLXLYLZL,簡記為L坐標系,主要用于確定載體相對于北、東和地方向的姿態;

5)載體坐標系OBXBYBZB,簡記為B坐標系,主要用于描述載體的姿態(通常為俯仰角、橫滾角和偏航角)。

導航應用中的測量計算如姿態、位置、速度、加速度、角速度等參數,常常需要在這些不同坐標系之間進行平移和旋轉變換計算,而一般矢量物理量的測量中,最常用到的是其中的B坐標系以及N和L坐標系間的變換計算。

1.2 歐拉角

如圖1(a)所示,固定坐標系OXgYgZg(通常為L坐標系)和載體坐標系OXYZ有共同原點,ON為OXgYg平面和OXY平面的相交線,ON與平面ZgOZ垂直,稱為節線。

由坐標系OXgYgZg到OXYZ的轉換步驟為:以軸OZg和OZ為基本軸,其垂直面OXgYg和OXY為基本平面。首先,在坐標系OXgYgZg中繞OZg軸逆時針方向(從OZg軸正向看)旋轉角度α,OXg軸到達ON;再繞ON軸逆時針旋轉角度β,OZg軸到達OZ;最后繞OZ軸逆時針旋轉角度γ,ON軸到達OX,得到坐標系OXYZ。這種定義對應的3個角度(α,β,γ)稱為歐拉角,其名稱來源于天文學,最早由歐拉在1776年提出,其中β稱為章動角,α稱為進動角,γ稱為自轉角[5]。

圖1 兩種不同順序歐拉角定義示意圖Fig.1 Schematic diagram of definition of Euler angles in 2 different orders

實際上,對歐拉角的名稱、符號以及旋轉順序并沒有統一的規定,使用時必須先明確定義。圖2(a)是按照Z軸-X軸-Z軸依次旋轉的順序,稱為ZXZ順序,也稱為313順序,或者按照中間字母X區分稱為X順規(實際上X順規有4種不同形式);對應定義的歐拉角可以稱為Z-X-Z順序歐拉角。合乎規則的順規共有12種,分別是:ZXZ,ZXY,YXZ,YXY,XYX,XYZ,ZYX,ZYZ,XZX,XZY,YZX,YZY。歐拉角及其旋轉變換作為一種純粹的數學概念,12種合乎規則的順規都是可用的,不同順規對應不同的歐拉角和不同的旋轉變換矩陣。

1.3 歐拉角旋轉變換

在慣性導航等運動分析中,常常使用Z-Y-X順序定義歐拉角,實際上不同的旋轉順序對應不同的旋轉變換矩陣和旋轉結果,一種旋轉結果可以對應許多組不同的旋轉歐拉角。為了與常用的姿態角定義和測量計算方法一致,這里選擇Z-Y-X順序歐拉角(ψ,θ,φ)對歐拉角旋轉變換進行分析。

如圖1(b)所示,固定坐標系OXgYgZg(一般是L坐標系中的NED坐標系)和載體坐標系OXBYBZB有共同原點O,OXgYgZg依次經過Z、Y、X軸3次連續旋轉,得到OXBYBZB,具體旋轉過程及其坐標變換如下:

首先,坐標系繞Z軸旋轉,旋轉角度ψ為正(沿Z軸正方向看,逆時針方向旋轉ψ角度定義為正角度,下同),由OXgYgZg旋轉到OX1Y1Z1,此時OZ1軸與OZg軸重合;

第二步,坐標系繞Y軸旋轉正角度θ,由OX1Y1Z1旋轉到OX2Y2Z2,此時OY1軸與OY2軸重合;

第三步,坐標系繞X軸旋轉正角度φ,由OX2Y2Z2旋轉到OXBYBZB。

在上述每一步變換中,按照同一矢量在2個不同坐標系中的正交分解進行計算,求解同一矢量在不同坐標系中的量值關系,最后得到:

式中:Xg=[xg,yg,zg]T和XB=[xB,yB,zB]T分別是同一矢量X在OXgYgZg和OXBYBZB坐標系中的3個正交分量;是由OXgYgZg旋轉到OXBYBZB的方向余弦矩陣;CgB是由OXBYBZB旋轉到OXgYgZg的方向余弦矩陣,它們是互逆的正交矩陣,因此,

方向余弦矩陣的具體表達式如下:

應用到矢量物理量的測量變換中,姿態測量傳感器固定在載體坐標系中,該坐標系從固定坐標系OXgYgZg以Z-Y-X順序經歐拉角(ψ,θ,φ)旋轉到OXBYBZB,在載體坐標系OXBYBZB中的測量結果為XB。如果姿態測量傳感器測量得到的角度值是前述歐拉角(ψ,θ,φ),使用上面的公式,對在載體坐標系中的傳感器測量值XB進行修正,可以求出所測量的矢量值在固定坐標系OXgYgZg中的3個分量,即求出Xg。

1.4 無限小角度轉動

在上述Z-Y-X順序歐拉旋轉中,如果轉動歐拉角(ψ,θ,φ)為無限小角度值,則在以歐拉角形式表示的方向余弦矩陣中有以下近似:

忽略二階及以上乘積項如sinθsinφ、sinψsinφ、sinψsinθsinφ等小角度乘積項,則方向余弦矩陣可以近似簡化為

可以看出,當轉動歐拉角為無限小角度值時,以歐拉角形式表示的方向余弦矩陣均為對稱矩陣,矩陣乘法的順序不影響乘法結果。也就是說,當轉動歐拉角為無限小角度值時,將轉動分解為3次連續歐拉旋轉,結果與旋轉順序無關。在慣性導航等設備的應用中,設備測量載體的姿態角度時,量化速率比較高,相當于每次疊加計算所對應的轉動角度均為無限小角度,可以采用上述對稱矩陣形式的方向余弦矩陣進行近似求解,大大簡化求解過程,提高計算速度[5]。

2 姿態角及其坐標變換

2.1 姿態角

姿態角也是一組能夠完整表述剛體相對于參照坐標系轉動位置的參量,包括偏航角、俯仰角和滾轉角,其中的俯仰角和滾轉角通常為傾斜角。姿態角的參照固定坐標系通常為L坐標系中的北東地(NED)坐標系[6]。

圖2 載體姿態角定義示意圖Fig.2 Schematic diagram of definition of carrier's attitude

按歐拉角定義方法來定義固定坐標系和載體坐標系,在載體坐標系OXYZ中,OX軸相對于固定坐標系OgXgYgZg的水平面以及OgXg(正北方向)、OY軸相對于OgXgYgZg的水平面,存在3個偏角,它們反映了載體的姿態,稱為載體的姿態角,通常用(ψ,θ,φ)表示,參見圖2,具體定義如下。

偏航角ψ:載體坐標系X軸在水平面上投影與固定坐標系Xg軸之間的夾角,由載體X軸的投影線逆時針轉至Xg軸時,偏航角為正,即機頭右偏航為正,反之為負。偏航角通常也稱為方位角或航向角。

俯仰角θ:載體坐標系X軸與水平面的夾角。當X軸的正半軸位于過坐標原點的水平面之上(抬頭)時,俯仰角為正,否則為負。

滾轉角φ:有2種定義,第一種定義為載體坐標系Z軸與包含載體X軸的鉛垂面間的夾角,用φz表示,第二種定義為載體坐標系Y軸與水平面的夾角,用φy表示;載體向右滾為正,反之為負。滾轉角的兩種定義在實際工程計算中都有人使用。

旋轉歐拉角主要是一種數學上的概念,姿態角的定義更具物理意義,容易通過測角傳感器測量得到。但是,由于各種測角傳感器的原理各異,具體使用時,需要明確傳感器輸出角度值的物理意義,以及滾轉角的具體定義,準確使用姿態修正變換公式。

2.2 姿態角坐標變換中的問題

前面的歐拉旋轉變換公式是基于3個歐拉角及其旋轉順序推導的,不同的旋轉順序對應不同的變換系數矩陣,它表明即使是相同的旋轉角度,不同的旋轉順序對應的最終旋轉結果也是不同的。

從歐拉角和姿態角的定義看,歐拉角和姿態角是不同的角度,因此,在矢量物理量測量及其坐標變換修正中,應仔細考慮角度測量傳感器所測量角度的實際物理意義;否則直接將姿態角測量值當作旋轉歐拉角,應用前述歐拉角旋轉變換公式(1)和(2)進行坐標變換修正計算,可能存在原理性誤差。

在實際工程應用中,角度測量傳感器一般都是基于載體坐標系的,通過與載體固定連接,實時測量載體的姿態角度。各種不同的姿態角度測量傳感器,往往原理不同,性能特點各異,適用的環境條件各不一樣。常用的測角傳感器有加速度計、磁力計、陀螺儀以及以陀螺儀為核心的慣導系統(包括平臺式慣導系統和捷聯慣導系統)等。

2.3 由加速度計求解傾斜角

加速度計也稱重力感應器或力感應器,主要是通過測量組件在某個軸向的受力情況來計算軸向加速度的大小和方向。由于重力加速度只是地表垂直方向加速度,因此,借助三軸加速度計可以測得一個固定平臺相對地球表面的運動方向[7]。

通常加速度計的測量值包含了重力加速度和其它受力運動產生的加速度,而在靜態、勻速運動或接近勻速運動的低速(即維持慣性)條件下,可以認為或近似認為只有重力而無其它作用力,測量的三軸加速度值認為是重力加速度產生的,由三軸加速度測量值可以求解載體的傾斜角度(姿態角中的2個量)。

實際上,以下2種求解過程是互為逆運算關系:1)已知固定坐標系下重力加速度的3個分量,通過加速度計測量載體坐標系下的重力加速度,求解載體的傾斜角度;2)已知或者測量獲得載體坐標系的傾斜角度,通過測量載體坐標系下的重力加速度的3個分量,求解固定坐標系下的重力加速度值。

圖3 加速度計測量計算姿態角的原理示意圖Fig.3 Principle diagram of measuring attitude angles by accelerometer

下面來推導由加速度計求解傾斜角度的具體求解過程。

如圖3所示,OXgYgZg為固定坐標系,OXYZ為載體坐標系,三分量加速度計固聯在載體坐標系的坐標軸上。圖中將水平面OXgYg旋轉到了鉛錘面上。

在OXgYgZg坐標系中,重力加速度的值為G=[Gx,Gy,Gz]T=[0,0,g]T,g為重力加速度常數;在OXYZ坐標系中,加速度計的測量值為g=[gx,gy,gz]T。

我們假定由坐標系OXgYgZg到坐標系OXYZ是經過Y-Z順序2個歐拉旋轉實現的,旋轉的具體步驟:

1)在OXgYgZg坐標系內,繞OYg軸(順螺旋方向,即逆時針方向)旋轉θ角,即OXg軸和OZg軸均在OXgZg平面內旋轉了θ角度,得到坐標系OX′Y′Z′,其中Y′與Yg重合;

2)在OX′Y′Z′坐標系內,繞OX′軸(順螺旋方向,即逆時針方向)旋轉φ角,即OY′軸和OZ′軸均在OY′Z′平面內旋轉了φ角度,得到坐標系OXYZ,其中X與X′重合。

至此,可以得到以下一些關系:

1)OX軸在OXgZg平面內,因此θ等于OX軸與水平面OXgYg的夾角,即目標的俯仰角;

2)OY′與OYg重合,OYg⊥OXgZg平面,因此平面OY′Z′⊥OXgZg平面(即鉛錘面),OZ′為相交線;OY′、OY、OZ′、OZ在同一平面OY′Z′內,OY和OZ在OXgZg平面上的投影均為OZ′;因此,OZ軸與鉛錘面OXgZg的夾角等于φ,也就是滾轉角的第一種定義值φz=φ;

3)假設OY軸在水平面OXgYg上的投影為OP,OY與水平面OXgYg的夾角即為滾轉角的第二種定義值φy。用φy和φ兩個角度分別計算OY軸上的單位矢量在OZg上的投影分量,則有:sinφy=sinφcosθ。

根據以上關系,重力加速度在OXgYgZg坐標系中的值G=[Gx,Gy,Gz]T=[0,0,g]T與加速度計的測量值g=[gx,gy,gz]T之間,滿足歐拉角旋轉變換關系,即:

由Gx=0和Gy=0可以得到:

由上式推導出:

所以,由加速度計求解傾斜角的計算方法:

1)在載體坐標系中測量3個正交加速度計的值gx,gy,gz;

2)用上述2個式(4)和式(5)求解出θ和φ;

3)俯仰角為θ;

4)滾轉角φ的第一種定義值為φz=φ,第二種定義值φy由關系式sinφy=sinφcosθ求解;

由加速度計求解傾斜角適用于靜止、勻速或近似勻速運動的條件。在不考慮偏航角的情況下,可以通過測量傾斜角對矢量測量值進行傾斜修正。

假設在載體坐標系下測量得到的矢量值為X=[x,y,z]T,載體坐標系的傾斜角(θ,φ)由傳感器測量得到,則將X轉換到固定坐標系下的值為Xg=[xg,yg,zg]T,按照公式(3),得到:

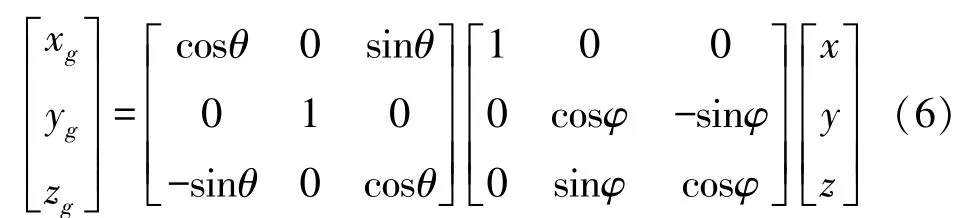
式中:θ為俯仰角測量值;滾轉角φ的傳感器測量值如果為第一種定義φz,則φ=φz,為第二種定義φy時,則由sinφ=sinφy/cosθ計算得出φ。

2.4 由磁力計求解偏航角

磁力計也稱為磁感器,可用于測試磁場強度和方向,原理類似指南針。

在地球表面,地磁場始終是沿著磁感應線(地磁場的磁力線)指向北的,某點的磁場強度方向為磁感應線在該點的切線方向,它在北向和垂直方向有相應的分量,在東西方向的分量為0。因此,在固定坐標系下,地磁場矢量可以表示為Mg=[Mxg,Myg,Mzg]T=[Mxg,0,Mzg]T,即Myg=0。如圖4所示,地磁場強度總量為Mg,其北向分量為Mxg=Mgcosδ,垂直分量為Mzg=Mgsinδ,東向分量為Myg=0。

圖4 地磁場及其三分量指向示意圖Fig.4 Schematic diagram of geomagnetic field and its tricomponent

由此可以看出,在載體目標上安裝三軸磁力計,測量出三軸地磁場強度M=[Mx,My,Mz]T,就可以計算出載體坐標系的方位角(即偏航角)ψM。當然,實際上地球的地理北極和地磁南極并不重合,有一定的夾角,稱為磁偏角Δψ。根據經緯度可以查詢到該磁偏角Δψ的大小。固定坐標系的北向指向地理北極,磁力計求得的北向指向地磁南極,因此,用磁力計求解的方位角ψM需要進行磁偏角Δψ修正,才能得到地理方位,即真正的偏航角ψ[8]。

和加速度計的測量一樣,通常情況下,安裝磁力計的載體坐標系也是處于運動狀態,具有一定的傾斜角,因此,利用磁力計測量值求解方位時,也需要進行傾斜修正。

下面來推導由磁力計求解偏航角的具體求解過程。

假設在載體坐標系下測量得到的地磁場為M=[Mx,My,Mz]T,載體坐標系的傾斜角(θ,φ)通過加速度計求解得到,按照公式(6),可以將地磁場測量值M=[Mx,My,Mz]T進行傾斜修正,得到相對于固定坐標系OXgYgZg僅有偏航角ψM而無傾斜角的坐標系下的值Mp=[Mxp,Myp,Mzp]T:

而Mp=[Mxp,Myp,Mzp]T是由地磁場在固定坐標系下的值Mg=[Mx,0,Mzg]T經過旋轉偏航角ψM得到的,而且,這個偏航角的旋轉在傾斜之前或之后,結果都是一樣的。因此有:

式中:θ為俯仰角測量值,φ=φz(當滾轉角測量值為第一種定義值φz時)或者由計算式sinφ=sinψy/cosθ計算得到(當滾轉角測量值為第二種定義值φy時)。

再考慮磁偏角Δψ的修正,相對于固定坐標系的偏航角為:ψ=ψM+Δψ。

所以,通過測量或測量計算得到載體坐標系的傾斜角(θ,φ),以及載體坐標系下地磁場的值M=[Mx,My,Mz]T,可以求解偏航角ψM,再進行磁偏角Δψ修正,就可以求得相對于固定坐標系的偏航角ψ。最終得到載體的姿態角(ψ,θ,φ)。

2.5 姿態角的坐標變換計算

綜合前面的分析,在載體坐標系下測量某一矢量物理量時,同步測量載體的姿態角,通過姿態角的坐標變換,將載體坐標系下的矢量測量結果變換到固定坐標系。而姿態角與旋轉歐拉角在定義上是有區別的。因此,在姿態角的測量以及角度計算中,要明確角度輸出值的定義,特別是滾轉角的輸出值所對應的定義,引用合適的變換矩陣,而不能簡單直接地引用歐拉角旋轉變換公式。

一組姿態角對應一種旋轉結果,但一種旋轉結果可以對應多組旋轉歐拉角。下面以Z-Y-X旋轉順序為例,在前述傾斜角修正和偏航角修正算法的基礎上,推導姿態角與Z-Y-X順序歐拉角之間的關系。

圖5為姿態角與Z-Y-X順序歐拉旋轉角的關系示意圖。圖中的旋轉步驟如下:

1)固定坐標系為OXgYgZg,一般是L坐標系(其中的NED坐標系)。在坐標系為OXgYgZg內,繞OZg軸(順螺旋方向,即逆時針方向)旋轉ψ角,即OXg軸和OYg軸均在OXgYg平面(通常為水平面)內旋轉了ψ角度,得到坐標系OX1Y1Z1,其中OZ1軸與OZg軸重合,OX1軸和OY1軸均在OXgYg平面內;

2)在OX1Y1Z1坐標系內,繞OY1軸(順螺旋方向,即逆時針方向)旋轉θ角,即OX1軸和OZ1軸均在鉛錘面OX1Zg內旋轉了θ角度,得到坐標系OX2Y2Z2,其中OY2軸與OY1軸重合,OX2軸和OZ2軸均在鉛錘面OX1Zg內,OX2軸在水平面OXgYg上的投影為OX1軸;

3)在OX2Y2Z2坐標系內,繞OX2軸(順螺旋方向,即逆時針方向)旋轉φ角,得到坐標系OX3Y3Z3,其中OX3軸在與OX2軸重合,OZ3軸在鉛錘面OX1Zg上的投影為OZ2軸,OZ3軸與鉛錘面OX1Zg的夾角即是滾轉角的第一種定義,記為φz,顯然有φz=φ;而OY3軸與水平面OXgYg的夾角記為φy。

圖5 姿態角與Z-Y-X順序歐拉旋轉角的關系示意圖Fig.5 Schematic diagram of relation between attitude angles and Z-Y-X order

從坐標系OXgYgZg到OX3Y3Z3,根據姿態角的定義得到:ψ為偏航角,θ為俯仰角,φ為橫滾角第一種定義值,即φz=φ,下面來推導滾轉角第二種定義值φy的表達式。

假設OY3軸上有一個單位矢量uy3,在坐標系OXgYgZg上進行正交分解,它在OZg軸上的分量為sinψy;

如果在坐標系OX2Y2Z2上對uy3進行正交分解,它在OZ2軸上的分量為sinψy,在OY2軸上的分量為cosφ,在OX2軸上的分量為0;OY2軸上的分量為cosφ在坐標系OXgYgZg上進行正交分解,由于OY2在水平面OXgYg上,因此cosφ在OZg軸上分量為0;OZ2軸上的分量為sinφ在坐標系OXgYgZg上進行正交分解,它在OZg軸上分量為sinψcosθ。

OY3軸上的單位矢量uy3,用兩種不同的正交分解方法求解在OZg軸上的分量,結果應該相等,因此有:sinψy=sinψcosθ。

由此得出姿態角與Z-Y-X順序歐拉角的關系為:歐拉角ψ等于偏航角;歐拉角θ等于俯仰角;歐拉角φ與2種定義橫滾角的關系:φz=φ,sinψy=sinψcosθ。

因此,矢量物理量的姿態變換計算方法:假設載體坐標系下的矢量測量值為X=[x,y,z]T,載體坐標系的姿態角測量值為(ψ,θ,φ),則矢量X在固定坐標系下的修正結果Xg=[xg,yg,zg]T為

式中:ψ為偏航角測量值,如果偏航角是通過磁力計測量的,需要進行磁偏角Δψ修正;θ為俯仰角測量值;當滾轉角的測量值為第一種定義值φz時,φ=φz;當滾轉角測量值為第二種定義值φy時,由計算式sinφ=sinφy/cosθ計算得到φ。

姿態角的取值范圍為:ψ,φ∈[-π,π],θ∈[-π/2,π/2]。

2.6 陀螺儀和慣導系統測量姿態角的比較

陀螺儀也稱作地感器,由陀螺構成的慣導系統,無論是傳統的機械轉子陀螺平臺式慣導系統,還是新型光纖陀螺捷聯慣導系統,都可以求解運動目標的瞬時速度、位置以及姿態角度[4,8]。

在傳統的機械轉子陀螺和平臺式慣導系統中,經過初始對準后,輸出的傾斜角是載體坐標系x、y軸相對于基準水平面的角度,而偏航角則是相對于正北方向的。俯仰角和偏航角與姿態角中的定義完全一致,滾轉角則與姿態角中的第二種定義一致,使用變換計算式(10)時,由計算得到φ。

而在捷聯慣導系統中,使用虛擬的數學平臺代替了物理平臺,陀螺測量的是載體相對于慣性坐標系的轉動角速度,然后通過計算得到載體的姿態角,具體計算過程為

1)陀螺儀測量,運用地球參數和位置參數計算;

3)用姿態四元數的元素表示姿態矩陣;

4)根據余弦矩陣和歐拉角定義,用歐拉角表示的姿態矩陣形式求解歐拉角(ψ,θ,φ)。

由上述導航解算原理可知,捷聯慣導系統實際給出的是Z-Y-X順序歐拉角,其中偏航角輸出已經修正為正北航向,俯仰角和滾轉角經過象限修正為歐拉角真值,滾轉角等同于姿態角中的第一種定義φz。坐標修正變換可以直接使用變換計算式(10),其中φ=φz。

3 結束語

在實施任意姿態(也就是載體坐標系)下矢量物理量的測量時,一般需要同步測量載體的姿態角,然后通過坐標變換公式對矢量測量值進行修正,求解出固定坐標系下的矢量值。

以測量水面艦船目標的磁場為例,測量時,目標在水面上,測量傳感器沉底布放,傳感器的姿態(包括方位)與確定的固定坐標系不平行,即存在一個傳感器坐標系,其姿態角可以測量,因此,對傳感器的測量結果,應該進行姿態角變換修正。

很多文獻和工程實踐中,無論是基于陀螺測量的姿態角還是其它傳感器測量的傾斜角,往往直接引用旋轉歐拉角坐標變換公式,進行測量數據修正和坐標變換計算。從前面的分析可以看出,各種不同的傳感器測量的姿態角,其輸出值所代表的物理意義不一定完全相同,特別是滾轉角存在兩種不同的定義,如果傳感器的滾轉角輸出值物理意義不同于歐拉角定義,直接引用旋轉歐拉角坐標變換公式,就會產生原理性誤差。

正確的做法是:分析姿態角傳感器的工作原理,明確姿態角測量值的定義,確定姿態角測量值與某種歐拉角(通常采用Z-Y-X順序歐拉角)的數值關系,再引用歐拉角修正變換計算式。

如果滾轉角輸出值對應第一種定義,即載體坐標系Z軸與包含載體X軸的鉛垂面間的夾角,則與旋轉歐拉角定義一致,可以直接引用旋轉歐拉角坐標變換公式;如果滾轉角輸出值對應第二種定義,即載體坐標系Y軸與水平面的夾角,則與旋轉歐拉角定義不一致,不能直接引用旋轉歐拉角坐標變換公式。

另外,在工程應用中,通常在靜態或接近靜態條件下,使用低成本的傾斜儀測量傾斜角,使用磁方位儀測量方位角,滾轉角測量值為第二種定義值,在坐標變換修正計算中應用前述公式(10)時,由計算φ。在運動狀態下,一般使用陀螺儀或基于陀螺儀的慣導系統測量姿態角。如果是傳統的機械轉子陀螺或者平臺式慣導系統,姿態角測量值與傾斜儀+磁方位儀相同,滾轉角測量值為第二種定義值,坐標變換修正計算中應用前述公式(10)時,由計算φ;現在更廣泛使用的是光纖陀螺捷聯慣導系統,姿態角測量值一般為Z-Y-X順序歐拉角,滾轉角測量值為第一種定義值φz,在坐標變換修正計算中應用前述公式(10)時,φ=φz。