基于低頻學習的電液位置伺服系統魯棒自適應控制
劉雷, 姚建勇, 馬大為, 王廣文
(南京理工大學 機械工程學院, 江蘇 南京 210094)
0 引言
電液位置伺服系統具有抗負載剛性大、響應快及功率密度大等突出優點,在國防和很多重要民用工業領域[1-2]都得到了廣泛應用。同時電液位置伺服系統也是一個典型多因素影響的強不確定非線性系統[3-4],包含許多非線性特性和模型不確定性[5],其中模型不確定性又可分為參數不確定性[6]和不確定性非線性[7]兩類。近年來,隨著電液位置伺服系統向高精度、高頻響的方向發展,對系統跟蹤性能的要求越來越高,電液位置伺服系統中固有的非線性特性和各種不確定性因素,尤其是系統存在高頻干擾和傳感器測量噪聲,使得傳統的線性控制策略難以滿足系統的高性能要求,迫切需要先進的非線性控制策略。
為了獲得高性能的跟蹤效果,各種非線性控制方法相繼被提出。針對系統存在的非線性特性,反饋線性化控制策略被引入,通過在控制器設計中對非線性項進行前饋補償以使誤差動態線性化。由于自適應控制技術處理參數不確定性問題的優越性,考慮到系統的不確定性,許多學者提出了各種自適應控制器,如基于反演設計[8]的非線性自適應控制、自適應反饋線性化技術、自適應魯棒、期望補償[9]以及基于干擾觀測器的控制[10]等。這些控制器不僅很好地解決了不確定性系統的控制問題,而且相比于線性控制器有更好的控制性能。實際系統的機械柔度、高壓流體的流態等均表現為高頻干擾,加之傳感器本身的精度,難以保證準確地測量物理量,系統很難取得滿意的跟蹤性能。為了保證系統的跟蹤誤差,通常會增大自適應律增益,但這在實際運用中很可能激發高頻顫振,進而引發系統的不穩定,甚至發散[11]。Yucelen等[12-13]提出了基于參考模型的低頻學習自適應控制理論,在系統不發生高頻顫振的情況下,通過提高增益達到快速自適應的目的,并通過仿真驗證了這種低頻學習方法[14-15]的有效性。
基于以上分析,本文針對電液位置伺服系統存在的高頻干擾和傳感器測量噪聲導致傳統自適應控制參數收斂性差、性能一致性低等問題,提出一種基于低頻學習的魯棒自適應控制策略。通過在傳統自適應律基礎上引入基于低通濾波的修正項,以盡可能消除自適應律中的高頻成分,調整修正增益,從而使得系統自適應參數穩定收斂,提高系統跟蹤性能。
1 系統建模與問題描述
電液位置伺服系統如圖1所示,其慣性負載動力學方程為
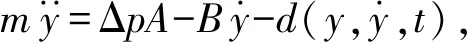
(1)
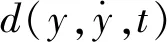

圖1 電液位置伺服系統結構簡圖Fig.1 Structure diagram of electro-hydraulic position servo system
忽略外部泄露,液壓缸左右兩腔的壓力動態方程為
(2)
式中:VL和VR分別為液壓缸左右兩腔的容積,VL=VL0+Ay,VR=VR0-Ay,VL0和VR0分別為液壓缸兩腔初始容積;βe為液壓油的有效彈性模量;qL和qR分別為左右兩腔的建模誤差;Δq為內部泄露量,Δq=CtΔp,Ct為液壓缸內泄露系數。
Qs和Qr與伺服閥的閥芯位移xv的關系為
(3)
式中:kq為流量增益;
(4)
由于實驗使用的是高頻響伺服閥,其閥芯位移與輸入近似為比例環節,即xv=kiu,ki為位置常數,因此從(4)式可知,s(xv)=s(u),進而(3)式可以寫為
(5)
式中:kt=kqki為總流量增益。

(6)
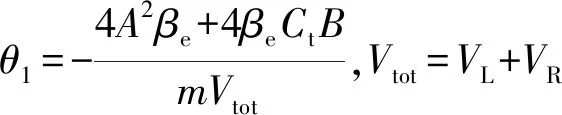
對于大多數應用場合,結構化和非結構化的不確定性程度是已知的,因此以下假設總是成立的。
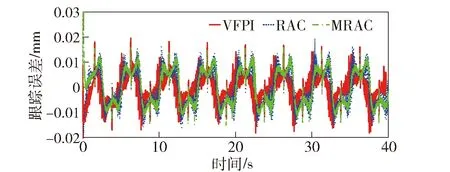
假設1電液位置伺服系統在正常工況下工作,兩腔壓力pL和pR需滿足0 假設2期望位置指令3階連續且可微。 假設2為基于模型的非線性控制基本假設,現實中不連續的測試信號(如階躍信號等)可通過恰當的軌跡規劃來滿足此假設。 假設3系統參數集滿足 θ∈Ωθ={θ:θmin≤θ≤θmax}, (7) 式中:θmin=[θ0min,θ1min,θ2min,θ3min]T、θmax=[θ0max,θ1max,θ2max,θ3max]T是已知的;Ωθ表示參數范圍的集合。 假設4f(x,t)足夠光滑且滿足 |f(x,t)|≤d, (8) 式中:d為擾動的上界且為未知常數。 在設計之前,引入一個足夠光滑的單調函數w(t)且滿足: (9) 式中:μ、μ*為正常數。 (10) 式中:i=0,1,2,3;τi為自適應函數。令 (11) 式中:Γ為對角自適應矩陣,其具有以下屬性: (12) 定義如下誤差變量: (13) 結合(6)式和(13)式可得 (14) 基于(6)式,設計的實際控制輸入和自適應函數τ分別為u=ua+us和τ=φz3, (15) 式中:ua為模型補償項;us為魯棒項;k3和ks均為正的反饋增益;為d的估計;w(t)>0為單調遞減函數;φ=[1,x2,x3,ua]T為回歸向量。 (16) 式中:Γf>0為參數自適應增益。 J(, (17) J(,f)為關于的負梯度,即修正項的結構: (18) 將(18)式代入(11)式,得 (19) 式中:σ>0為修正系數。 選取Lyapunov函數 (20) (21) 最后根據引理及運用楊氏不等式,將(16)式、(19)式代入(21)式,整理可得 (22) 對(21)式積分可得 (23) 為驗證所提的控制策略,實驗結果采用4種性能測量指標(最大值、平均值、標準差、歸一化的控制輸入變化量)來評價跟蹤的性能,分別定義如下: 1) 跟蹤誤差的最大絕對值Me: (24) 式中:N為記錄的數字信號數量。 2) 跟蹤誤差的平均值ε: (25) 3) 跟蹤誤差的標準差δ: (26) 4) 歸一化的控制輸入變化量Lc: (27) 式中:u(i)為控制輸入;Δt為采樣間隔。 實驗平臺如圖2所示,液壓缸系統參數見文獻[16-18],(0)=[0 m2·Pa/(s·kg),-10 000 m·Pa/K,-40 N·s/(m·kg),210 m2·Pa/(s·V·kg)]T,θmax=[100 m2·Pa/(s·kg),1×106m·Pa/K,100 N·s/(m·kg),600 m2·Pa/(s·V·kg)]T,θmin=[-1.2×106m2·Pa/(s·kg),-1×108m·Pa/K,-1×107N·s/(m·kg),8 m2·Pa/(s·V·kg)]T,1(0)=0 m2·Pa/(s·kg). 其中,向量(0)中各元素代表參數θ的初始估計值,1(0)代表參數d1的初始估計值。考慮到實驗臺采用的是高精度傳感器,一般工程應用中傳感器的精度比較低,為了與實際狀況具有可比性,不失一般性,以及驗證所提出算法的有效性,采用數字模擬的形式在實驗室傳感器測得的物理量中加入高頻噪聲和高頻干擾模擬信號,在所有測試工況中均選擇幅值為1×10-5~1×10-4的虛擬隨機高頻白噪聲信號,并將之加入實際系統位置測量中。 圖2 電液位置伺服系統實驗平臺Fig.2 Experimental platform for electro-hydraulic position servo system 選取以下3種控制策略進行實驗對比: 1)基于低頻學習設計含有修正項的魯棒自適應控制器(MRAC),具體形式為(15)式、(19)式; 2)電液位置伺服系統魯棒自適應控制器(RAC),具體形式為(11)式、(15)式; 3)電液位置伺服系統速度前饋PI控制器(VFPI),具體形式為 (28) 式中:e1(t)=x1-xd為位置誤差;kv=35.55 s·V/mm為系統速度常數;kP、kI分別為比例常數、積分常數。 選取期望指令信號xd=10arctan(sin(πt))·(1-e-t)/0.785 4 mm. 各控制策略參數取值如下: 1)MRAC參數:k1=1 800,k2=600,k3=105,ks=1,λ=0.01,Γ0=1 000 m·Pa/kg,Γ1=1.15×106s·Pa/kg,Γ2=2.65×104N·s2/kg,Γ3=5×10-4m·Pa/(V·kg),σ0=5×10-6s-1,σ1=1×10-8s-1,σ2=0.15 s-1,σ3=1×10-6s-1,Γf0=5 m·Pa/kg,Γf1=2 s·Pa/kg,Γf2=2 N·s2/kg,Γf3=0.5 m·Pa/(V·kg); 2)RAC參數:k1=1 800,k2=600,k3=105,ks=1,Γ0=1 000 m·Pa/kg,Γ1=1.15×106s·Pa/kg,Γ2=2.65×104N·s2/kg,Γ3=5×10-4m·Pa/(V·kg),λ=0.01; 3)VFPI參數:kP=8 000,kI=2 000. 圖3 0.5 Hz工況下參數θ和d1估計Fig.3 θ and d1 estimations at 0.5 Hz 圖3所示為參數自適應過程,從圖3可以看出,相比于傳統的RAC,帶有修正項的MRAC可以濾除系統中的高頻成分,使參數自適應的收斂更穩定,有效地防止了參數的漂移,同時在控制策略設計中補償了此修正的影響,確保了系統的跟蹤精度。圖4所示為各控制器輸入的變化情況,圖5所示為各控制器作用下系統位置的跟蹤誤差對比,表1為最后兩個跟蹤周期的各項性能指標。由以上數據可知,本文所提出的MRAC控制效果在跟蹤誤差的最大值、平均值、標準差等方面均優于RAC和VFPI. 圖4 0.5 Hz工況下控制輸入對比圖Fig.4 Comparison of control inputs at 0.5 Hz 圖5 0.5 Hz工況下跟蹤誤差對比圖Fig.5 Comparison of tracking errors at 0.5 Hz表1 0.5 Hz工況下性能指標表Tab.1 Performance indices at 0.5 Hz 控制策略Me/mmμ/mmδ/mmLc/mmVFPI0.06820.01950.01260.0106RAC0.04380.00870.00720.0099MRAC0.03590.00730.00570.0099 圖6 0.5 Hz工況下MRAC壓力曲線圖Fig.6 Pressure signals of MRAC system at 0.5 Hz 系統參數取值同0.5 Hz工況,期望指令信號為xd=10arctan(sin(0.4πt))(1-e-t)/0.785 4 mm,0.2 Hz工況中各控制策略參數取值同0.5 Hz工況。 3種控制器作用下系統位置的跟蹤誤差如圖7所示,其各項性能指標如表2所示。由于MRAC中的修正項可以濾除系統中的高頻成分,頻率越高干擾的頻率也隨之升高,此時這種控制器的作用越明顯,可以看出MRAC的控制性能整體上優于其他兩種控制器,且相比于上述兩種工況,控制輸入的顫抖惡化程度更小。由此可以看出MRAC的控制性能整體上優于其他兩種控制器。 圖7 0.2 Hz工況下跟蹤誤差對比圖Fig.7 Comparison of tracking errors at 0.2 Hz 表2 0.2 Hz工況下性能指標表Tab.2 Performance indexes at 0.2 Hz 控制策略Me/mmμ/mmδ/mmLc/mmVFPI0.01830.00370.00290.3080RAC0.01950.00660.00270.2794MRAC0.01520.00660.00240.2739 本文根據液壓缸非線性數學模型建立了狀態方程,基于狀態方程,經過一系列公式推導出了魯棒自適應控制器;針對高頻干擾和傳感器測量噪聲引起的傳統自適應控制參數收斂性差、性能一致性低等問題,在魯棒自適應控制器的基礎上,提出一種基于低頻學習的控制策略,并且基于Lyapunov穩定性理論證明了系統的全局穩定性;通過實驗進行了驗證。得出以下結論: 1)設計的修正項可以濾除自適應律中的高頻成分,避免由此引起的高頻顫振,有效降低了參數的高頻波動,防止了自適應參數的漂移,同時控制輸入的顫抖程度得到了有效的改善。 2)基于低頻學習設計的魯棒自適應控制器保留了漸進跟蹤的性能,對比實驗結果表明跟蹤誤差幅值也有較大程度的降低。 考慮到液壓管路的動態、伺服閥自激諧振等因素會對電液位置伺服系統高頻動態行為產生重要影響,后續將針對這些影響因素開展更深入的研究。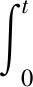
2 控制器的設計

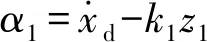
3 新型參數自適應律的設計


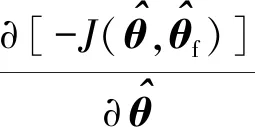

4 穩定性證明


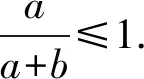
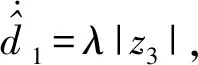
5 實驗結果分析
5.1 實驗參數及性能指標

5.2 0.5 Hz工況下的實驗結果

圖6為MRAC作用系統的壓力曲線。



5.3 0.2 Hz工況下的實驗結果

6 結論

