廣義核-衛星圖的無符號拉普拉斯譜*

田貴賢, 孫 眉

(浙江師范大學 數學與計算機科學學院,浙江 金華 321004)

0 引 言

圖的譜不僅能很好地反映圖的結構(如簡單圖恰有一個正特征值當且僅當它是一個完全多部圖；若圖的代數連通度大于0,則其必連通[1-2]等),而且圖的譜也可以用來研究圖的其他性質，如圖的能量[1]、生成樹的數量[2-3]、(度)基爾霍夫指數[4-5]、整譜圖的構造[6-7]等等.

本文主要研究核-衛星圖和廣義核-衛星圖的無符號拉普拉斯譜.

設G=(V,E)是一個有n個頂點、m條邊的無向連通簡單圖，其中頂點集為V，邊集為E.用di表示頂點vi的度，即與頂點vi相關聯的邊的條數.圖G的鄰接矩陣A(G)=(aij)n×n是一個n階方陣，其元素滿足：若vi和vj相鄰，則aij=1；否則，aij=0.矩陣A(G)的所有特征值的集合稱為G的譜.用D(G)=diag(d1,d2,…,dn)表示圖G的度對角矩陣,稱L(G)=D(G)-A(G)為圖的拉普拉斯矩陣;稱矩陣L(G)的所有特征值的集合為G的拉普拉斯譜;稱Q(G)=D(G)+A(G)為圖G的無符號拉普拉斯矩陣;稱矩陣Q(G)的所有特征值的集合為G的無符號拉普拉斯譜.

設G1=(V1,E1)，G2=(V2,E2)是2個簡單圖.若圖G1∪G2=(V,E)的點集為V=V1∪V2,邊集為E=E1∪E2，則稱G1∪G2是G1與G2的并.若圖G1G2=(V,E)的點集與邊集分別為V=V1∪V2和E={eij|?vi∈V1,vj∈V2}∪E1∪E2，則稱G1G2是G1與G2的連圖.為簡單起見，η個G的并，記為ηG.

定義1[8]設c≥1，s≥1，η≥2.稱圖Θ(c,s,η)?Kc(ηKs)為以Kc為核團、以η個Ks為星團的核-衛星圖，其中Kc表示c個點的完全圖.

由于在現實世界的復雜網絡模型中，并非所有的星團都相同.因此，需要進一步考慮將核-衛星圖推廣到具有多個不同星團的情形.

定義2[8]設si≥1,ηi≥1,i=1,2,…,t.稱圖Θ(c,s,η)?Kc(η1Ks1∪η2Ks2∪…∪ηtKst)為廣義核-衛星圖，其中s=(s1,s2,…,st),η=(η1,η2,…,ηt).

顯然，核-衛星圖Θ(c,s,η)是廣義核-衛星圖Θ(c,s,η)的特殊情形，即t=1時的情形.

近些年，運算圖的各類譜得到廣泛研究，如Indual[6]引入了細分點、細分邊連圖的概念并刻畫了它們的鄰接譜與因子圖的鄰接譜之間的關系,也構造了一些整譜圖；文獻[4]進一步刻畫了細分點、細分邊連圖的鄰接譜，拉普拉斯譜，以及無號拉普拉斯譜與因子圖的相應譜之間的關系，也構造了一些同譜圖對,并計算了上述圖類生成數的數目和基爾霍夫指數；文獻[9]又將上述部分結果推廣到更一般的情況，即將點連和邊連的情況同時進行考慮，給出了雙連圖的概念.同時,也刻畫了關于細分圖、R-圖、Q-圖及全圖的雙連圖的拉普拉斯譜.最近,文獻[7,10]也刻畫了幾類特殊的連圖的無符號拉普拉斯譜，進一步構造了一些無符號拉普拉斯整譜圖.廣義核-衛星圖是區別于文獻[4,6,9]中的連圖變異類的一種特殊的連圖,在現實世界的復雜網絡模型中有著廣泛的應用.Estrada等[8]研究了該圖的聚類系數、度匹配系數,并通過構造特征值及對應的特征向量刻畫這類圖的鄰接譜和拉普拉斯譜.

受上述研究的啟發，本文將研究核-衛星圖和廣義核-衛星圖的無符號拉普拉斯譜.通過構造核-衛星圖和廣義核-衛星圖的特征值及對應的特征向量，得到它們的無符號拉普拉斯譜與核團、星團的結構關系.作為應用,本文也構造了一些無符號拉普拉斯整譜圖，推廣了文獻[7，10]的部分相關結果.

1 廣義核-衛星圖的無符號拉普拉斯譜

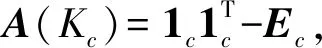
給定廣義核-衛星圖Θ(c,s,η)，定義c×(ηisi)階矩陣

和(ηisi)×(ηisi)階準對角矩陣

其中:對角塊上共有ηi個A(Ksi);i=1,2,…,t.

適當排列廣義核-衛星圖Θ(c,s,η)點的次序可以將其鄰接矩陣表示成如下的分塊形式：

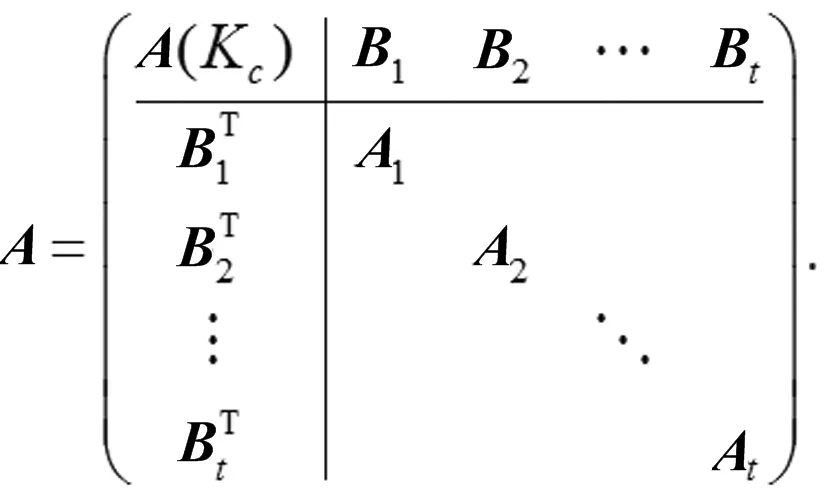
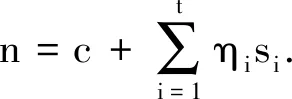
Q=A+D=

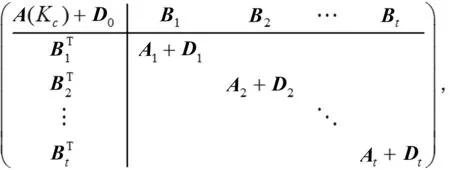
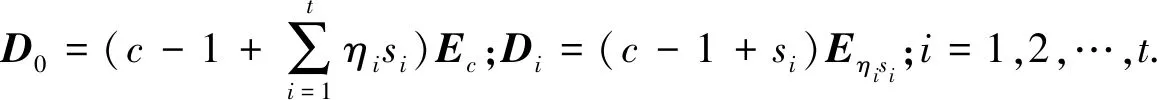
定理1廣義核-衛星圖Θ(c,s,η)的無符號拉普拉斯譜由下列特征值構成：

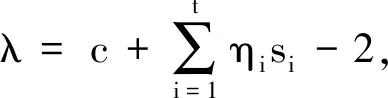
2)特征值λ=si+c-2，其重數為ηi(si-1)；

3)特征值λ=2si+c-2，其重數為ηi-1；

4)余下特征值是下列方程的根：

證明 注意到完全圖Kc的譜為{c-1(1),-1(c-1)}，其中a(b)表示a重復b次.顯然，1c是屬于特征值c-1的特征向量.假設x1是屬于特征值-1的特征向量,令向量

(1)

其分塊方法與Q相同.那么特征方程Qx=λx等價于

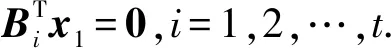
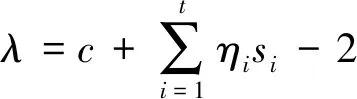
令向量

(2)

其分塊方法與Q相同.那么特征方程Qx=λx等價于

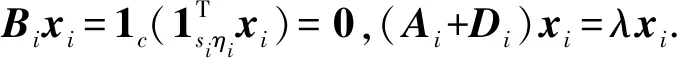
λ=-1+(si-1+c).

由于Kc屬于特征值-1的線性無關的特征向量有si-1個,而同一類星團的個數為ηi,故特征值λ=si+c-2的重數為ηi(si-1).

令非零向量

其中,x中的非零塊出現在對應于Q中的對角線塊Ai+Di的位置上，且分塊方法與Q相同.因此，由特征方程Qx=λx可得

其中,Di1=Di2=…=Diηi=(c-1+si)Esi.從而上式等價于(A(Ksi)+Dij)1si=λ1si,j=1,2,…,ηi.故

λ=si-1+(si-1+c).

再由方程α1+α2+…+αηi=0的解空間的維數是ηi-1可得λ=2si+c-2的重數為ηi-1.

最后,分2種情況討論余下的t+1個特征值 .當t=1時,該圖為核-衛星圖Θ(c,s1,η1).令向量

其分塊方法與Q相同.由特征方程Qx=λx可得

上式表明:

2(c-1)+η1s1+βη1s1=λ;

c+β(2(s1-1)+c)=λβ.

消去β可得

進而有

λ2-(η1s1+3c+2s1-4)λ+

(η1s1+2c-2)(c+2s1-2)-cs1η1=0.

解此二次方程可得

下面假設t>1，令向量

其分塊方法與Q相同.顯然,這種形式的向量與式(1)和式(2)中的所有特征向量都正交.對于這樣的向量，由Qx=λx可得

所以

(3)

c+βi(2si-2+c)=λβi.

(4)

整理可得,

所以

該方程決定了廣義核-衛星圖Θ(c,s,η)的剩余t+1個特征值.定理1證畢.

例1設廣義核-衛星圖Θ(c,s,η)=Θ(2,23,15)如圖1所示.

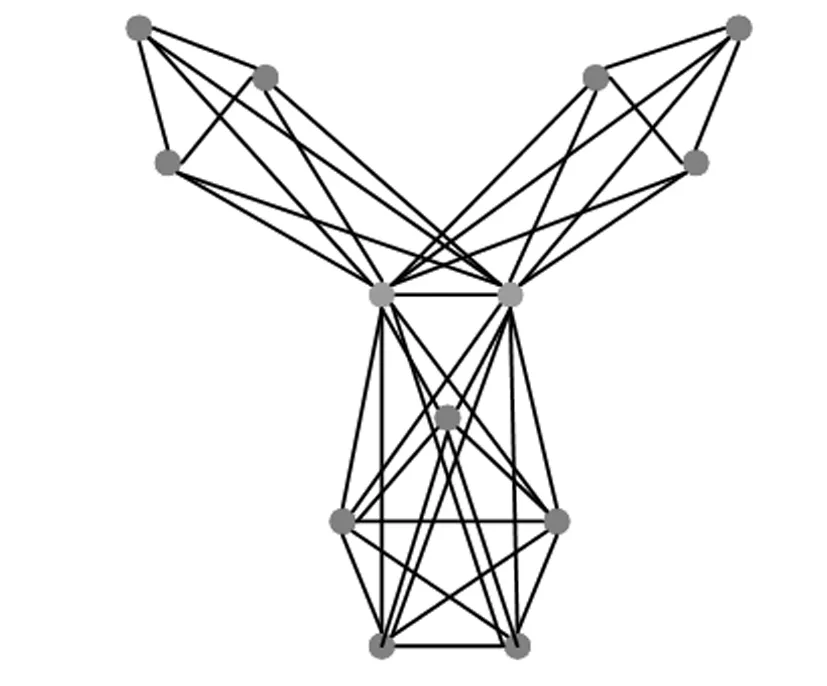
圖1 廣義核-衛星圖Θ(2,23,15)

由定理1可得其無符號拉普拉斯譜特征值為：

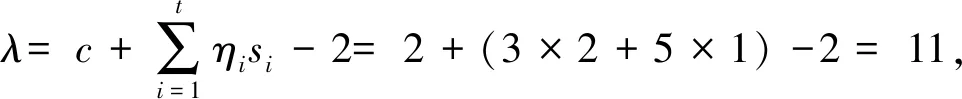
2)λ=s1+c-2=3,其重數為η1(s1-1)=4,λ=s2+c-2=5,其重數為η2(s2-1)=4;

3)λ=2s1+c-2=6,其重數為η1-1=1;

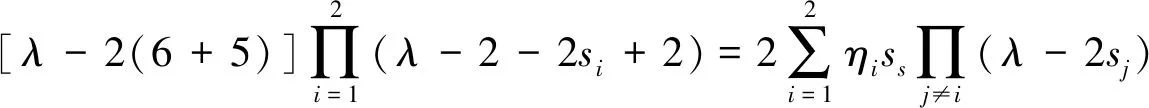
λ3-29λ2+246λ-600=0?

λ1=15.905 0,λ2=8.815 9,λ3=4.279 1.

通過Matlab直接計算，可得Θ(2,23,15)的無符號拉普拉斯譜為{11,3(4),5(4),6,15.905 0,8.815 9,4.279 1}，進一步驗證定理1成立.

在定理1中令t=1,可得核-衛星圖Θ(c,s,η)的無符號拉普拉斯譜.

定理2核-衛星圖Θ(c,s,η)的無符號拉普拉斯譜由下列特征值構成：

1)特征值λ=c+ηs-2，其重數為c-1；

2)特征值λ=s+c-2，其重數為η(s-1)；

3)特征值λ=2(s-1)+c，其重數為η-1；

4)余下2個特征值為

例2設核-衛星圖Θ(2,2,3)如圖2所示.

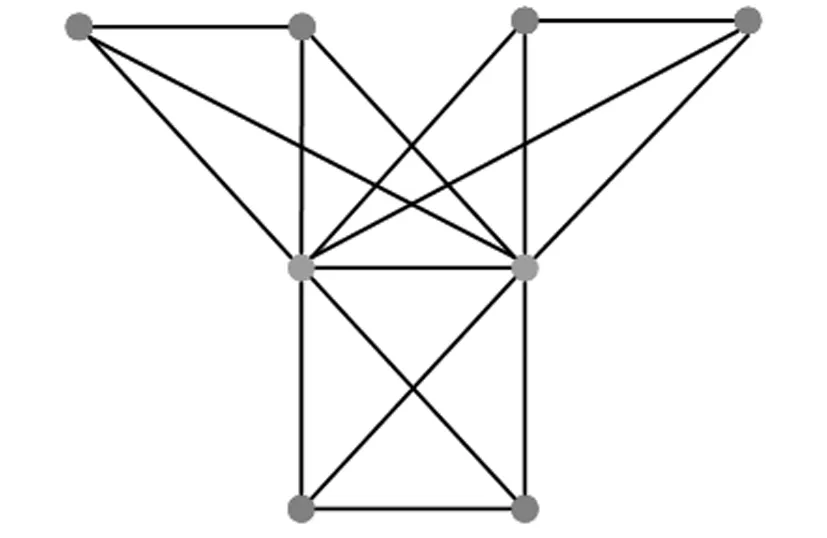
圖2 核-衛星圖Θ(2,2,3)

由定理2可得其無符號拉普拉斯特征值為：

1)λ=c-2+ηs=6,其重數為c-1=1;

2)λ=s+c-2=2,其重數為η(s-1)=3(2-1)=3;

3)λ=2(s-1)+c=2(2-1)+2=4,其重數為η-1=3-1=2;

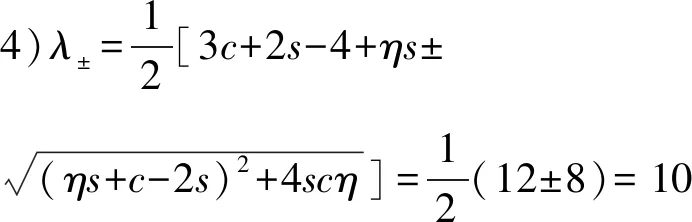
用Matlab直接計算可得Θ(2,2,3)的無符號拉普拉斯譜為{2(4),4(2),6,10}，進一步驗證定理2成立.

在定理2中,若令c=m,s=1,η=n,則

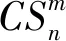
m(n-1); (n+m-2)(m-2).

其中，a(b)表示a重復b次.

眾所周知，整譜圖的構造是圖譜理論研究的重要課題，文獻[7]研究了正則圖的連圖的無符號拉普拉斯譜，并構造了一些無符號拉普拉斯整譜圖.直接利用定理2,可得核-衛星圖Θ(c,s,η)是無符號拉普拉斯整譜圖的充分必要條件,該結果推廣了文獻[7]中的主要結果.

定理3核-衛星圖Θ(c,s,η)是無符號拉普拉斯整譜圖的充分必要條件是

(ηs+c-2s)2+4scη∈Z2.

證明 定理2表明核-衛星圖Θ(c,s,η)是無符號拉普拉斯整譜圖當且僅當

是整數.由于ηs+3c+2s-4與(ηs+c-2s)2+4csη有相同的奇偶性,故λ±是整數當且僅當

(ηs+c-2s)2+4scη∈Z2.

定理3證畢.

直接應用定理3,可得:

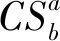
在定理1中,若令t=2,η1=η2=1,即廣義核-衛星圖僅含有2個不同的星團，則

推論3[7]廣義核-衛星圖Θ(c,s,η)?Kc(Ks1∪Ks2)是無符號拉普拉斯整譜圖的充分必要條件是(c+2s1+2s2)2-16s1s2∈Z2.

證明 由定理1知,Kc(Ks1∪Ks2)是無符號拉普拉斯整譜圖當且僅當三次方程

(λ-2c-s1-s2+2)(λ-2s1-c+2)×

(λ-2s2-c+2)=

c(s1(λ-2s2-c+2)+s2(λ-2s1-c+2))

的根是整數.根據三次方程的求根公式,類似于定理3的證明可得結論成立.推論3證畢.

推論4[7]對于n∈Z+,1≤j<2n，圖Kj(K2n-j∪Kn)是無符號拉普拉斯整譜圖.特別地，圖Kn(Kn+2∪Kn+1),Kn+2(Kn∪Kn+1),K1(K2n-1∪Kn)和K2n-1(K1∪Kn)也都是無符號拉普拉斯整譜圖.

2 結 語

本文刻畫了廣義核-衛星圖的無符號拉普拉斯譜,應用所得結果給出了幾類圖是無符號拉普拉斯整譜圖的充要條件.由于廣義核-衛星圖是一種特殊的連圖,因此本文結果進一步表明,圖的運算(如連運算、冠運算、積運算等)是構造無符號拉普拉斯整譜圖的有效方法.另外, 廣義核-衛星圖是現實世界的復雜網絡模型之一,有著廣泛的應用背景.顯然, 對于復雜網絡中的其他模型,也可以考慮刻畫其無符號拉普拉斯譜及相關問題.