高光譜圖像波段選擇的改進二進制布谷鳥算法

宋廣欽，杜正舜，賀 智

(1. 中山大學地理科學與規劃學院綜合地理信息研究中心，廣東 廣州 510275; 2. 廣東省城市化與地理環境空間模擬重點實驗室，廣東 廣州 510275)

高光譜遙感是當今遙感技術的前沿，與多光譜遙感相比，其具有獨特的光譜分辨率(通常達到10 nm或更精細數量級)，能準確區分地物的細微差異，具有準確識別地物類型的潛能。目前高光譜遙感圖像已廣泛應用于多個領域，如地質勘探、精準農業和軍事用途[1]。但是，高光譜圖像波段多且波段之間具有較高的冗余性，易產生Hughes現象，不利于后續處理[2]，對高光譜圖像進行降維處理顯得尤為重要。剔除冗余和噪聲波段，選擇在圖像中起主要作用且相關性較低的波段，能在保證地物識別精度的前提下有效提高計算速度[3]。因此，波段選擇是高光譜數據降維的主要途徑之一，探究波段選擇方法對高光譜遙感圖像處理研究有著重要意義。

常用的波段特征選擇算法主要有Relief算法和最小冗余最大相關算法(minimum redundancy maximum relevance,mRMR)。其中，Relief算法通過計算特征與類別相關程度的權重進行波段選擇，該算法較為簡單且運行效率高，但不能有效去除冗余特征[4]。mRMR算法通過計算特征與類別最大相關性，以及特征與特征之間最小冗余性來進行特征選擇，但獲得的結果難以反映不同特征對分類作用的差異[5]。為了更好地解決復雜的目標尋優問題，有學者提出了通過模擬生物行為習慣或自然現象的仿生智能算法[6]，如遺傳算法(genetic algorithm,GA)[7]、蟻群算法(ant colony optimization,ACO)[8]、粒子群算法(particle swarm optimization,PSO)[9]、布谷鳥算法(cuckoo search,CS)[10]等。其中，CS算法的參數較少且穩健性較強，具有較好的尋優能力[11]。為了應用CS算法解決離散型目標尋優問題，有學者提出了二進制布谷鳥算法(binary cuckoo search，BCS)[12]。在高光譜降維研究中，有學者應用BCS算法進行波段選擇實現降維并取得較好的試驗結果[13]，但是BCS算法存在后期不能很好均衡全局性與收斂性及后期搜索效率低等缺點[14]。

基于以有研究，本文從兩方面對現有BCS進行改進：①使用混合二進制編碼算法更新子代鳥巢；②通過遺傳交叉更新被發現鳥巢位置，得到改進二進制布谷鳥算法(improved binary cuckoo search，IBCS)并運用于高光譜圖像波段選擇，然后與BCS算法及其他常用智能算法進行對比分析。

1 改進二進制布谷鳥算法波段選擇方法

1.1 標準布谷鳥算法

CS是由文獻[10]于2009年結合布谷鳥種類的巢寄生繁殖行為和Levy飛行特征提出的一種全局搜索算法。該方法采用Levy飛行游走及偏好隨機游走方式，使得全局搜索和局部搜索能力得到平衡，從而具有較好的尋優能力。在繁殖期間，布谷鳥會隨機選擇鳥巢進行產蛋，尋找鳥巢的游走方式是較短距離與偶爾長距離交替進行，搜索得到最優的鳥巢來對鳥蛋進行孵化，以達到高效的尋優效果。

CS算法為了更好擬合布谷鳥的巢寄生繁殖行為，假設了以下3個理想狀態：

(1) 每只布谷鳥只對應一個鳥巢和一個蛋，并且隨機選擇鳥巢。

(2) 在所有隨機選擇的鳥巢中，最優質的鳥巢會被保留給下一代。

(3) 可利用的鳥巢總數不變，鳥巢中的布谷鳥蛋被宿主發現的概率為Pa，Pa∈[0,1]。宿主發現后，會舍棄該鳥巢。

基于以上3個理想狀態，布谷鳥使用Levy飛行模式更新尋優鳥巢位置的公式如下

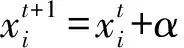
(1)

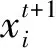
1.2 標準二進制布谷鳥算法的波段選擇

假設鳥巢總數為n，高光譜遙感圖像波段數為d，X=X1,X2,…,Xn代表一個布谷鳥種群，X(0)表示初始布谷鳥種群，X(t)表示第t代布谷鳥種群，波段集合b=b1,b2,…,bd代表高光譜數據集D中的d個特征波段，x=(x1,x2,…,xd)為二進制向量，xi∈(0,1)，基于BCS進行高光譜遙感圖像波段選擇主要步驟如下：

(1) 初始化n個原始鳥巢。在t=0時刻對n個鳥巢進行初始化并對第1～d個波段進行二進制編碼。初始化公式為

xi=random{0,1}

(2)

式中，random0,1代表隨機產生0或1。xi=1表示第i個波段被選擇，反之，xi=0表示第i個波段未被選擇。

(2) 計算種群鳥巢適應度。選擇適應度函數并計算每一個鳥巢的適應度值，得到當前的最優適應度值。由于鳥巢的適應度值可用來判斷鳥巢的優劣程度，因此構造合適的適應度函數是篩選出最優鳥巢的關鍵步驟。本文使用的適應度函數如下

(3)

式中，overall是分類器對鳥巢中所選擇的波段進行分類得到的總體精度，本文采用支持向量機(support vector machine,SVM)[15]作為分類器；bands為鳥巢中所選擇的波段數目；λ為控制系數。

(3) 更新群體鳥巢位置。對于第t步的可行解，使用Levy飛行的二進制變換公式進行位置更新。再次對更新位置后的鳥巢進行適應度計算，并且與上一代最優適應度值進行對比，保留具有更優適應度值的鳥巢，從而使得鳥巢的更新是朝著更優質鳥巢的位置方向進行。

(4) 更新被發現鳥巢。位置更新后，將(0,1)范圍的隨機數r與宿主發現概率Pa進行對比，Pa∈[0,1]。若r>Pa，則使用步驟(1)中初始化方法對鳥巢位置進行隨機更新，反之則不變，比較后保留最優質的鳥巢。

當迭代次數到達設定次數時，終止循環，輸出全局最優的鳥巢，該鳥巢所選擇的特征即為算法最終篩選出的目標波段。算法操作流程圖如圖1所示。

1.3 改進二進制布谷鳥算法的波段選擇

本文對標準二進制布谷鳥算法中的更新子代鳥巢位置方式和更新被發現鳥巢位置方式進行改進，使用混合二進制編碼更新子代鳥巢并使用遺傳交叉方式更新被發現鳥巢位置(如圖1的虛線框所示)。下面對這兩方面的改進進行重點闡述。

1.3.1 使用混合二進制編碼算法更新子代鳥巢

為了解決離散型尋優問題，有學者基于PSO算法提出了二進制粒子群算法(binary particle swarm optimization，BPSO)[16]。借鑒BPSO的構建方法，學者基于CS算法構建了Levy飛行的二進制公式[12]，得到BCS算法中子代鳥巢位置更新公式

(4)

(5)

文獻[17]經分析BPSO算法后提出了優化后的BPSO變換公式。借鑒改進后BPSO變換公式，文獻[18]得出了Levy飛行的二進制變換公式

當Step≤0時

(6)

(7)

當Step>0時

(8)

(9)

式(4)—式(9)中，k=1,2,…,N，N為種群數；i=1,2,…,d，d代表波段數；Sig(Step)為Sigmond函數，自變量為Levy飛行步長Step；rand()表示產生的隨機數。

本文采用二進制編碼混合更新方法。當僅使用式(4)、式(5)進行二進制編碼更新時，算法全局性很強，但收斂性比較弱；僅使用式(6)、式(9)進行二進制編碼更新時，算法全局性較弱，但收斂性較強[18]。為了平衡算法全局性與收斂性、提高的算法性能，本文在二進制編碼更新過程中引入控制系數pr∈[0,1]。引入pr后的更新方法如下：

if rand()≤pr

使用式(1)、式(2)進行二進制編碼更新

Else

If Step≤0

使用式(3)、式(4)進行二進制編碼更新

Else

使用式(5)、式(6)進行二進制編碼更新

在進行混合更新過程中，若pr較大，則IBCS算法的全局性會比較強；若pr較小，則IBCS的收斂性會比較強。通過調整該系數能較好地平衡IBCS的全局性和收斂性。

1.3.2 基于遺傳交叉更新被發現鳥巢

在標準BCS中，當布谷鳥蛋被宿主發現時，布谷鳥會舍棄原有鳥巢并隨機尋找新的鳥巢，但直接進行簡單隨機游走獲得的新鳥巢位置并不理想。鑒于此，為了使BCS算法更新被發現鳥巢時能夠更好地利用已有資源，本文基于遺傳算法[19]中的交叉思想，利用現有資源交叉產生新的資源來選擇被發現鳥巢的位置，從而提高尋優效率。

首先，對新發現的N個鳥巢的位置進行隨機亂序操作并將結果暫存作為遺傳父代染色體，然后重復上一次的操作，將原來N個鳥巢的位置再次進行隨機亂序操作得到的結果暫存作為遺傳母代染色體。通過隨機數確定父代與母代交叉位置，交叉位置前面后的染色體部分進行交叉對調，獲得新的子代。

本文使用(0,1)范圍內的隨機數作為是否進行交叉的判斷。如果生成的(0,1)之間的隨機數小于預定的交叉率，則父代和母代進行交叉，否則，使用偏好游走更新被發現鳥巢位置。

2 試驗流程

2.1 數據介紹

試驗所采用的高光譜數據集共有兩個。一個數據集是來自ROSIS傳感器的圖像，圖像覆蓋區域為意大利的Pavia大學，由640×310個像元組成。該圖像光譜范圍為0.43—0.86 μm，共包括113個波段。地物真實圖像包含9種類型的地物。

另一個數據集為印第安納高光譜AVIRIS數據，圖像覆蓋區域為美國西北印第安納州某農林混合試驗場，由144×144個像元組成。AVIRIS獲得的圖像有224個波段，其光譜范圍為0.41—2.45 μm。在去除水汽吸收波段和低信噪比波段之后，參加處理的波段為200個。該數據真實圖像一共包含16類不同的地物。

兩幅高光譜遙感圖像均具有真實地物分類圖像，在進行精度評價時，直接使用真實圖像與分類圖像進行對比分析，更準確獲取分類后的總體精度。

2.2 參數設置

為了分析波段選擇效果，將本文提出的IBCS與BCS算法、常用二進制智能算法(遺傳算法(binary genetic algorithm,BGA)、BPSO、二進制蟻群算法(binary ant colony optimization,BACO))、mRMR算法、Relief算法進行對比。每個智能算法的循環迭代次數均設置為100次，具體參數設置如下：在BGA算法中，種群大小Numpop=15，選擇率Selectrate=0.5，變異率Variationrate=0.1，雜交率Crossrate=0.5；在BPSO算法中，粒子種群數N=15，加速常數C1=C2=2，粒子權重w=0.5；在BACO算法中，螞蟻數量N=15，信息素重要程度α=1，能見度β=0.0、3.0，信息素揮發ρ=0.5，信息素增強度Q=0.7。為了保證比較的一致性，對于兩種常用算法mRMR和Relief波段數本文設置為與IBCS所選出的相同。

通過對IBCS的介紹可知，該算法包含5個參數，即初始鳥窩數量Nest、宿主鳥發現寄生鳥蛋的概率Pa、進制控制系數Pr、雜交率Crossrate及迭代次數Iter。初始鳥窩數量和宿主鳥發現外來鳥蛋的概率大小對算法的搜索速度及收斂性有影響，雜交率和二進制控制系數決定了布谷鳥算法的搜索范圍，以及能否跳出局部最優解。通過對IBCS的參數重復調試對比，本文所使用的參數如下：鳥巢總數Nest=15，發現概率Pa=0.5，二進制控制系數Pr=0.5，雜交率Crossrate=0.5，迭代次數Iter=100。

2.3 結果分析

試驗環境為：Matlab R2016a平臺，CPU 2.30 GHz，8 GB RAM，Windows 10操作系統。采用SVM為分類器，兩個數據集的每類地物均隨機選取10個像元為訓練樣本，分類結果分別如圖2、圖3和表1—表4所示。其中，圖2、表1和表3為PaviaU數據結果，圖3、表2和表4為AVIRIS數據結果。

表1 PaviaU數據集智能算法分類結果

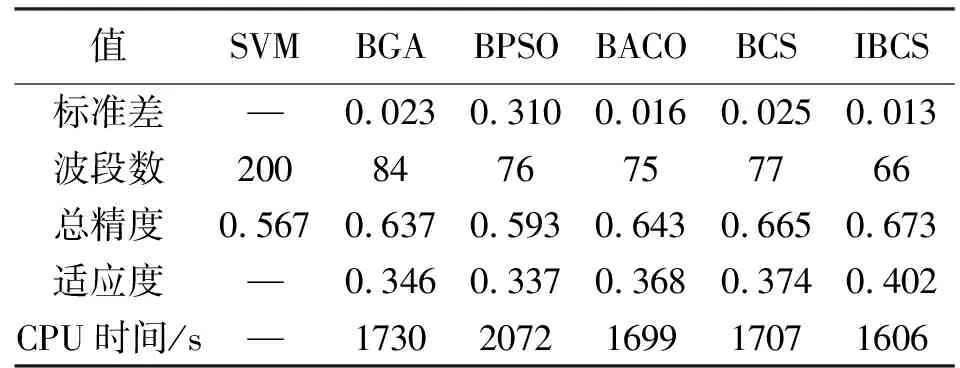
表2 AVIRIS數據集智能算法分類結果

由表1和表2可知，使用基于IBCS及其他智能算法的SVM分類結果精度高于單一使用SVM分類。在所選的智能算法中，IBCS算法獲得分類精度最高。其中，在Pavia數據集中，基于IBCS算法的分類精度得到顯著提高，達到76.8%，比單純使用SVM分類器的分類精度提升21.1%。對于PaviaU數據集及AVIRIS數據集，IBCS所選出的波段數分別為30和66，顯著降低了待處理數據維度。試驗結果說明IBCS算法能夠有效降低高光譜維數并且提高分類結果精度。

圖3 AVIRIS數據集分類結果

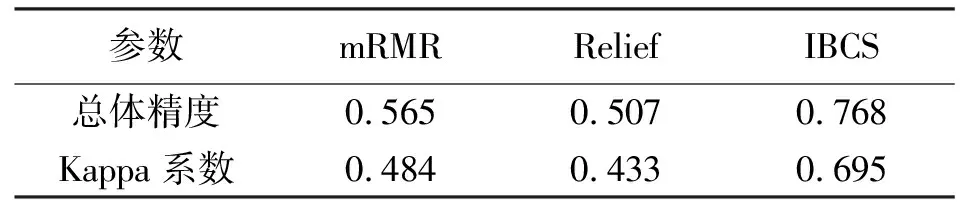
參數mRMRReliefIBCS總體精度0.5650.5070.768Kappa系數0.4840.4330.695

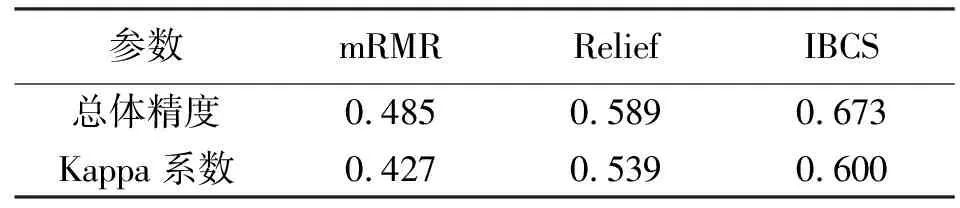
表4 AVIRIS數據集mRMR、Relief和IBCS算法分類結果

表1和表2的標準差為適應度的標準差，是指停止循環后所得到的多個解的標準差，可以用來反映智能算法最終的收斂性。由表1、表2可知，在試驗所用的智能算法中IBCS的標準差最小，說明IBCS收斂效果最好。在同樣迭代次數的情況下，IBCS耗時最短，說明IBCS具有更高的性能與更快的效率，是一種高效可靠的算法。

從表3和表4可以看出，在兩個數據集中，基于IBCS算法選擇的目標波段更具優勢，精度及Kappa系數相對于mRMR和Relief算法有所提高。結果表明IBCS算法具有更強的穩健性，優化效果更好。

3 結 語

本文提出了改進二進制布谷鳥算法對高光譜圖像進行降維，在BCS算法基礎上進行兩方面改進：①使用混合二進制編碼更新子代鳥巢均衡算法的全局性與收斂性；②使用遺傳交叉更新被發現鳥巢，加強利用已有資源提升算法尋優效率。試驗結果表明，IBCS與BCS、BGA、BPSO、BACO智能算法相比，具有能夠有效降低數據維度、后續分類精度更高、尋優效率更高等優點。相對于mRMR算法、RRelief算法，IBCS算法選擇的波段對高光譜圖像分類作用更大，能夠更好地提高分類精度。